汽车销量与新能源汽车关注度的格兰杰关系研究及预测

文/贺享悦 路子彤（中国地质大学[北京]）

一、数据获取与分析

（一）数据获取

1.全国乘用车销量

本文以月为单位，选取2017 年2 月-2021 年2 月间全国乘用车的实际销售量，来研究大数据搜索趋势与我国乘用车销售量之间的关系。所采集数据来源于NE 时代网站。

2.搜索指数

本文使用的搜索指数以“新能源汽车”关键词在搜索平台的搜索量为数据基础，计算关键词的搜索频次的加权和。由于搜索指数与全国乘用车销售量的单位不同，可比性不强，所以本文通过Z-Score 标准化：，其中。

将数据转化为无单位的Z-Score分值，使得数据标准统一化。

（二）相关性分析

本文通过使用斯皮尔曼相关系数对各平台关于“新能源汽车”关键字的发展趋势指数和全国乘用车销售量进行相关性分析，定量评估两者之间的关联性。本文选取了“360搜索指数”和“搜狗指数”两个指数与全国乘用车销售量进行相关性分析。由表1 和表2 可知，360 关注趋势指数与全国乘用车销售量显著相关；搜狗指数与之不存在相关性。因此，将针对360 搜索指数进行研究。

表1 “新能源汽车”关键词搜索指数和全国乘用车销售量的相关性检验

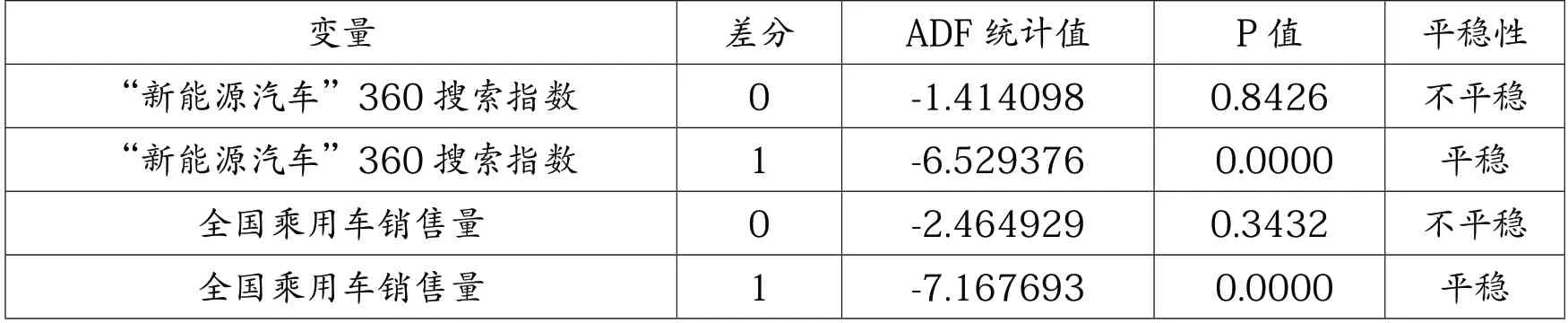
表2 单根检验结果

（三）季节性分解

本文选取了2017 年2 月-2021年2 月间全国乘用车实际销售量和“新能源汽车”搜索指数进行研究，由于两组数据都是以月度为时间序列数据，所以对数据进行季节性分解处理，使之更适用于长期趋势的研究。

（四）ADF 单根检验

本文采用ADF 检验法来检验时间序列的平稳性。首先对时间序列进行对数化处理，再对时间序列进行单根检验。由表3、表4 可知，360 搜索指数时间序列与全国乘用车销售量时间序列皆为1 阶平稳，为同阶平稳，符合协整检验的前提。

（五）协整检验及回归方程

经ADF 单位根检验可知全国乘用车销售量序列和“新能源汽车”360搜索指数序列虽自身非平稳，但是存在相似的趋势和增长变化，因此两者之间可能存在长期稳定的比例关系，并且两者均为一节单证序列，可以进行协整检验。

协整检验采用EG 两步法，首先对全国乘用车销售量序列和“新能源汽车”360 搜索指数序列进OLS 回归。设置“新能源汽车”360搜索指数为自变量ZHISHU，全国乘用车销量为因变量XIAOLIANG，进行OLS 推导，协整回归方程式如下：

其中ε 为残差项。

对ε 残差序列进行ADF 单位根检验，结果如表3 所示。

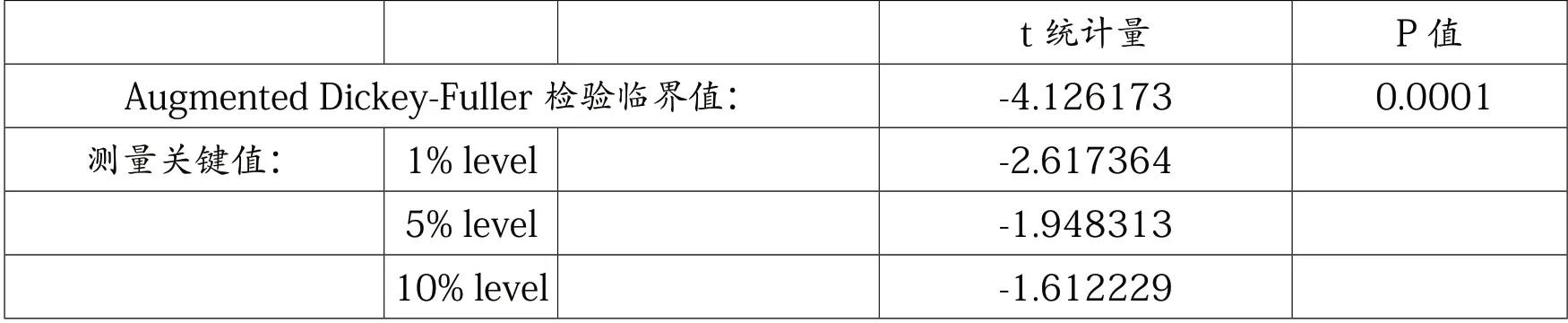
表3 对ε 残差序列进行ADF 单位根检验

由此可知，残差序列不存在单位根，表明该序列平稳。因此可以判断全国乘用车销售量和“新能源汽车”360 搜索指数之间存在长期均衡的协整关系。

（六）格兰杰因果检验

因为两组时间序列具有协整关系，所以本文使用格兰杰因果检验模型来检验预测能力。

首先对var 模型的稳定性进行检验。如图1 所示，点均落在单位圆内，对应的特征方程的特征根的绝对值小于1，模型稳定。

图1 VAR稳定性检验

如表4，根据赤池信息量准则（AIC）、施瓦茨准则（SC）及汉南-奎因准则（HQ）结果选取了最佳滞后阶段为2。

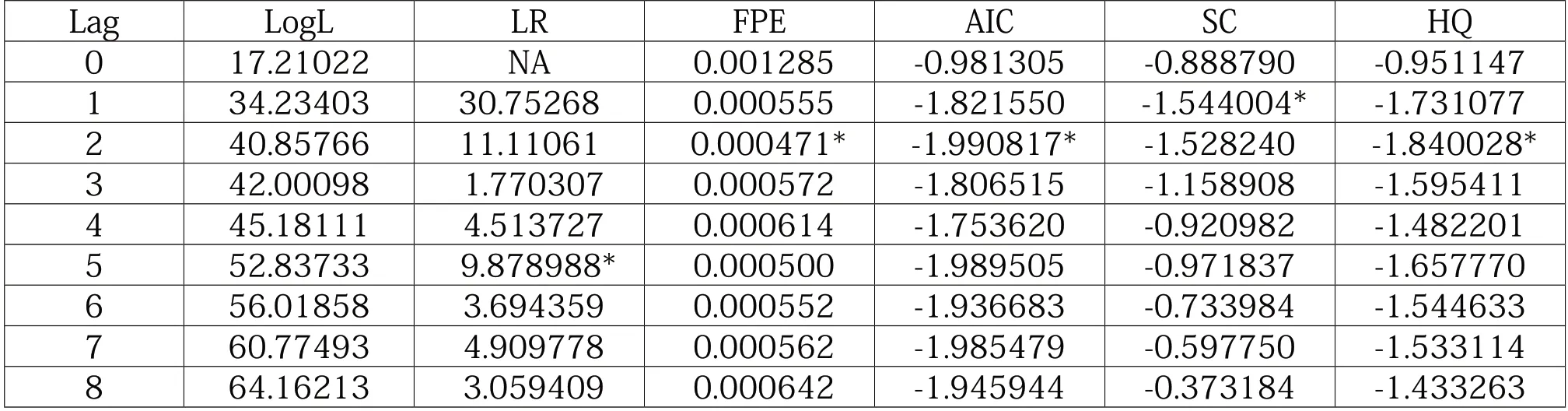
表4 确定VAR 模型滞后期

最后，进行格兰杰因果检验。由表5 可知，在5%的显著水平下，滞后二期的360 搜索指数是全国乘用车销售量的格兰杰原因。“新能源汽车”关键词的360 搜索指数对全国乘用车销售量的格兰杰原因的概率为99.01%，因此关键词“新能源汽车”的360 搜索指数可以作为一个有效的预测因子。

表5 格兰杰因果分析结果

二、预测模型建立与分析

为了进一步验证“新能源汽车”360 搜索指数对全国乘用车销量的预测能力，本文先以全国乘用车销量作为单一变量建立ARMA 模型，然后再加入搜索指数变量，建立多变量的VAR 模型，并对两种模型的预测结果进行对比。模型都以2017 年3 月-2020 年2 月的数据为样本期数据，2020 年3-9 月样本期外的数据为验证数据。

（一）ARMA 模型

通过观察对数化后的全国乘用车销量的自相关和偏自相关情况，本文建立并比较了几个不同的模型，最终选择拟合优度较高且AIC 与SC较小的ARMA(1,1）模型。得到预测结果如下：

销量(t)=1221497.8816+AR(1)*销量(t-1)+时间(t)+MA(1)*时间(t-1)

模型预测销售量和实际销售量的对比如图2 所示。

由图2 可以得出，该预测模型拟合程度相对较高。计算该预测模型的相关系数为0.89938145，拟合优度较高。

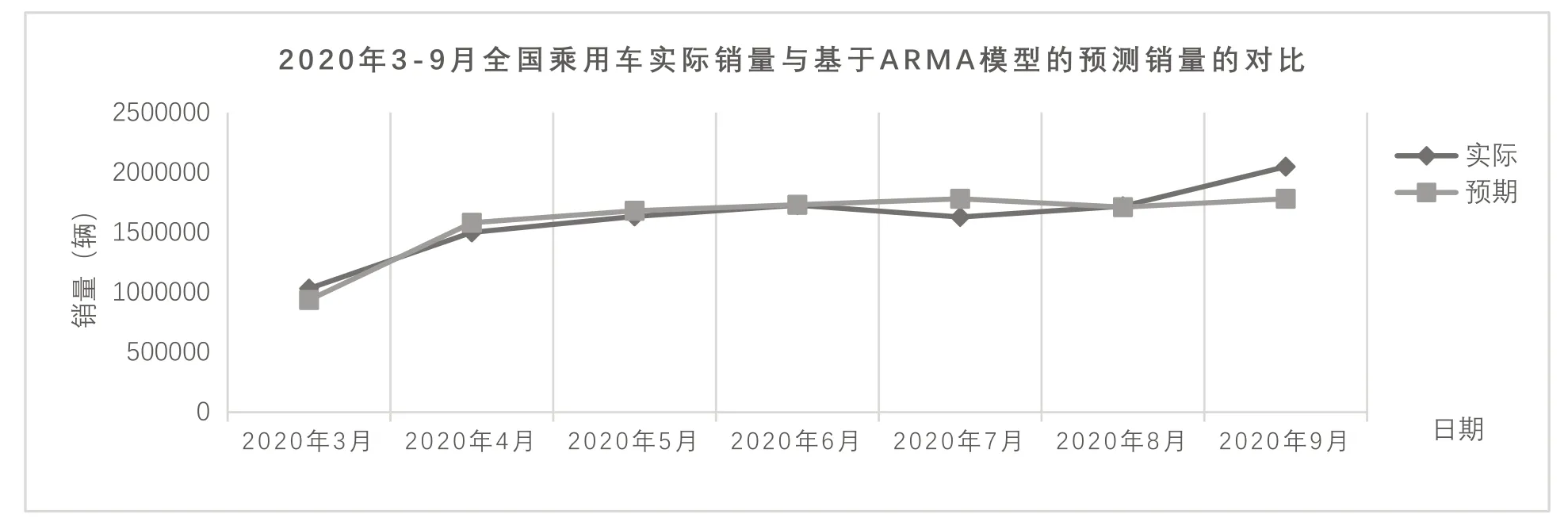
图2 2020年3-9月全国乘用车实际销量与基于ARMA模型的预测销量的对比

（二）VAR 模型

构建VAR 模型要确定VAR 模型的滞后阶段。本文通过比较，选择滞后阶数2 作为最佳滞后期建立VAR 模型。预测结果如下：

指数=0.862917095143* 指数(-1)-0.00323399781677* 销量(-1)+8147.97046981

销量=7.76447838425* 指数(-1)+0.303998512277* 销量(-1)+1133702.05388

预测2020 年3-9 月全国乘用车汽车月度销量数据对比，如图3所示。

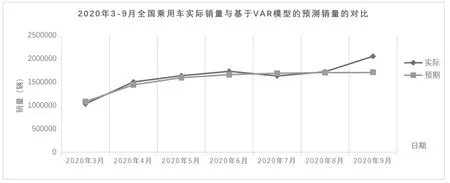
图3 2020年3-9月全国乘用车实际销量与基于VAR模型的预测销售量的对比

由表4 可知，VAR 模型对全国乘用车月度销量的平均预测误差为2.8635625%，预测精度比较高，计算预测数据与实际数据的拟合优度相关系数为0.918020769，比ARMA预测模型的相关系数高，由此表明运用VAR 模型预测全国乘用车月度销量的可行性和可靠性，具有更好的预测能力。

三、结论

“新能源汽车”360 搜索指数与全国乘用车销售量存在正相关，且存在长期均衡关系，因此可以使用“新能源汽车”360 搜索指数预测全国乘用车销售量。本文还选取了以“新能源汽车”作为关键词的搜狗指数，经过相关性分析可知，“新能源汽车”搜狗指数与全国乘用车销售量无相关性。说明尽管随着互联网的发展，各搜索指数反映网民关注趋势，但其数据价值有所差异。

加入搜索指数的VAR 模型相较于传统预测模型在样本期间内和样本期间外的预测精度均有较大提升。反映了“新能源汽车”360 搜索指数是一个有效的预测因子。该模型可以利用全国乘用车销售量前2 月的实际销售数据和搜索指数来预测一个月后对乘用车的需求，提高了预测的准确度和及时性，降低了对历史数据量的要求。

由研究表明，人们对新能源汽车的关注对汽车市场的发展有着重要的影响，说明新能源汽车是当前汽车市场的重要发展方向，具有重要地位。