装载机铲装物料动态称重数据处理方法研究*

张荣辉,黄 敏

(1.闽南科技学院,福建 泉州 362332;2.福建江夏学院 先进传感技术实验室,福建 福州 350108)

0 引 言

装载机动态称重是装载机智能化发展的趋势之一。结合动态称重技术可以实时监测装载机的负荷状态,防止装载机过载或者铲掘过少;不仅有利于提高装载机的作业效率,也为装载机作业的智能规划提供了重要参数。

但是,装载机的工作环境通常比较恶劣,例如矿山、崎岖山地、泥泞滩涂、狭窄或坡度较大的作业现场,因为环境引起车身不稳、碰撞振动等因素,会对装载机铲掘物料动态重量的稳定性、测量的准确度产生直接影响。

相较于常见的传感器外置物料称重方法(即基于压力传感器的直接称重法、应变片测量法等),抗干扰能力更强的传感器内置方法(即通过测量动臂油缸压力间接得到称重数据)已成为目前热门的动态称重方案。并且,这一方案的测量精度与模型的建立、数据的处理算法有关[1]。

BALLAIRE F等人[2]建立了装载机工作装置、动臂液压缸的动力学摩擦力模型,采集了各个部件的加速度,根据力矩平衡推出了物料重量;但由于该研究未对原始数据进行有效降噪,导致其最后称重结果误差较大。MINTAH B等人[3]提出了一套基于液压挖掘机的自适应负载监控系统,以工作周期为单位采集了铲斗运动速度及举升力,再把周期划分为多个数据段,选取有效数据段进行了物料重量的计算;但在实际应用中,周期内的数据段划分较难控制,使得该系统的使用局限性非常明显。王远见等人[4]建立了装载机的动力学模型,分析了影响称重的几个关键变量,如油压、动臂角度等,并对整个举升过程进行了计算;但该研究未对信号段进行识别处理,导致其计算的精度不佳。肖珊[5]使用小波分析算法对所采集的油压信号进行了预处理,对低频信号进行了分解与重构;但该研究未考虑到油压信号的中频部分,导致其称重结果的准确性不高。曹军杰[6]综合运用了虚位移原理及拉格朗日方程,推导出了完整的装载机工作装置动力学模型;同时加入了摇臂的影响因素,提出了模型中关键参数的辨识方法,为装载机的动态称重方法研究提供了模型支持和算法基础。

基于转动定律,笔者对某型号装载机铲掘作业相关部件进行动力学建模,通过合力矩分析得到铲斗内物料重量与动臂油缸油压、动臂举升角度之间的映射关系,结合数据线性段截取技术,重点对实车试验数据进行小波包降噪结合经验模态分解的二级降噪预处理,使称重结果较上述称重方案更加稳定和准确。

1 动态称重方案原理

1.1 装载机称重部件动力学建模

此处进行实车试验时,使用的是厦工机械某型号轮式装载机。

该装载机铲装部分的机械结构如图1所示。

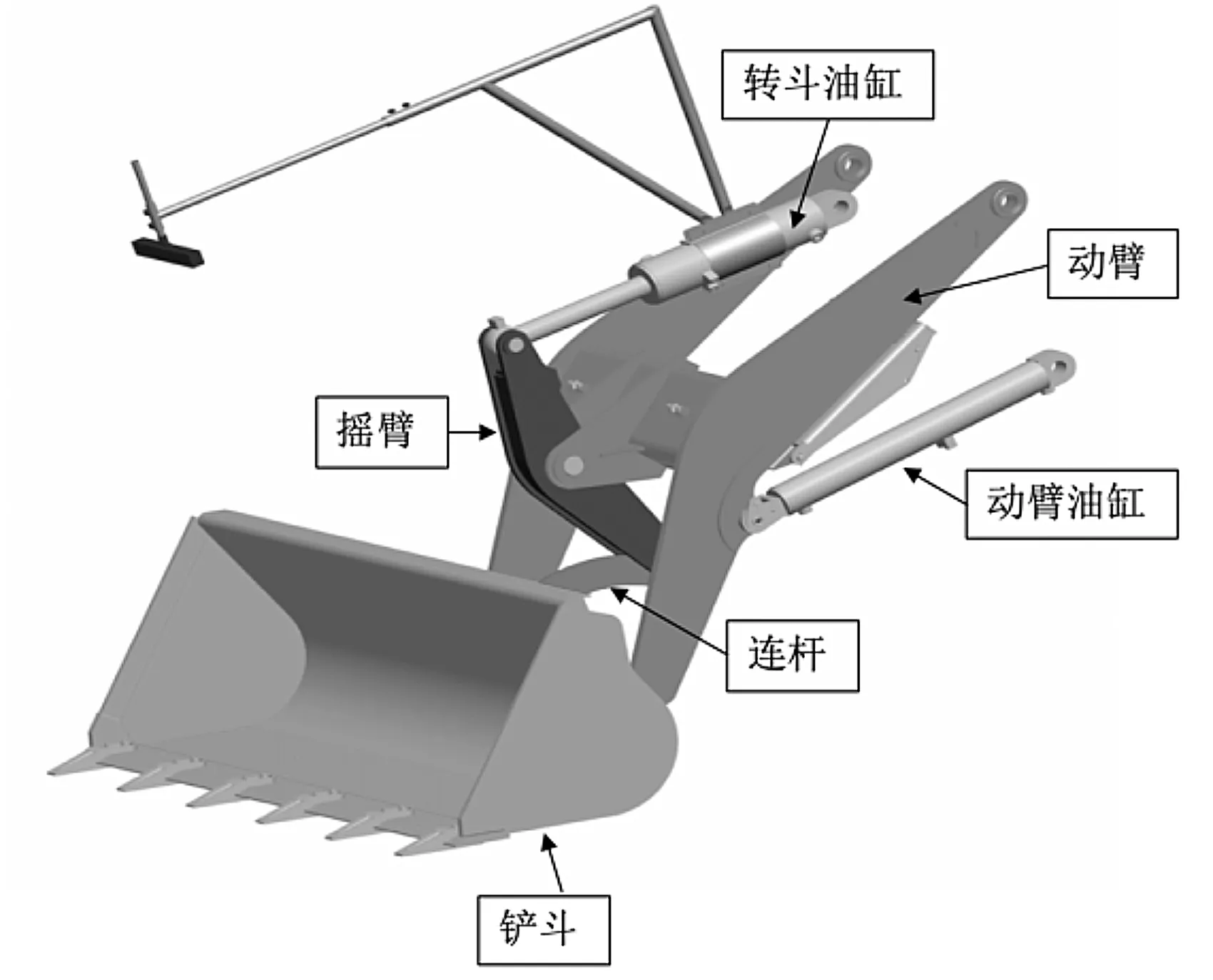
图1 装载机的铲装结构

图1展示了装载机与物料铲掘过程直接关联的机械结构:铲斗、摇臂、动臂、转斗油缸、动臂油缸、连杆。

笔者对上述这些部件组成的铲掘结构进行模型简化,其结果如图2所示。

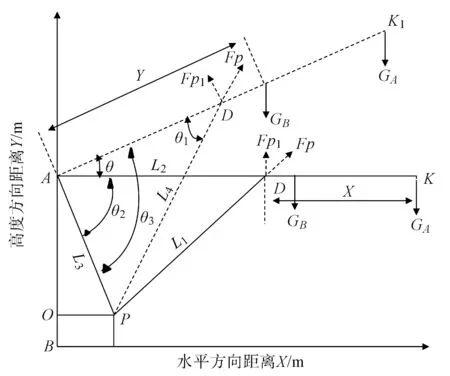
图2 装载机铲装结构的动力学模型A—动臂与机架座连接处的绞点;P—动臂油缸与机架座连接处的绞点;D—动臂油缸活塞与动臂的绞点;K—动臂与转斗连接处的绞点;AK—动臂初始位置;AK1—动臂举升后的位置;L1—动臂液压缸初始长度;L2—机架绞点A至活塞D的距离;L3—机架绞点A至机架座连接处的绞点P的距离;L4—动臂举升后动臂油缸的长度;GB—动臂与铲斗的重量质点;GA—物料的重量;θ—动臂举升角度;θ1—动臂与液压缸举升角度;θ2—动臂AK与AP之间的初始夹角;X—活塞绞点D到铲斗与动臂绞点K的距离;Y—绞点A到铲斗与动臂重心的距离

由转动定律可知,刚体定轴转动的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比。笔者针对该铲掘结构模型进行力学分析。

工作过程中,铲掘结构动臂AK所受的合力矩∑MA方程如下:

(1)

式中:J—AK绕绞点A的转动惯量;ω—AK绕绞点A的角速度;ε—AK绕绞点A的角加速度。

忽略摩擦力等外因影响,装载机动臂在转动过程中主要受到动臂油缸压力、动臂及铲斗自重以及物料重力的作用。

根据力学平衡原理,可推导出装载机铲掘结构动力学力矩∑MA表达式为:

∑MA=FpL2sinθ1-GBYcosθ-GA(L2+X)cosθ

(2)

式中:Fp—动臂油缸输出力,与动臂油缸压力及活塞截面有关。

动臂油缸输出力Fp表达式为:

Fp=PBSB-PASA

(3)

式中:SA—液压缸活塞上边缘面积;SB—液压缸活塞下边缘面积;PA—进口油压;PB—出口油压。

动力学力矩M和物料的重量GA如下:

(4)

为了便于计算,可选取动臂举升过程中趋于匀速的数据段,该段中的角加速度ε趋于0,则上述公式可简化为:

(5)

1.2 动态称重数据处理方法

在数据的采集过程中,因为驾驶员的人为误差(作业熟练性、规范性等)、环境干扰等因素会造成原始数据波动大、噪声干扰强,所以不能把原始数据直接代入模型中使用,需要对数据进行预处理,分解降噪。

此处笔者提出:首先,使用小波包进行初级分解去噪;然后,结合经验模态分解进行二级滤波,以得到连续性好、精度高、光滑度高的可用信号。

1.2.1 小波包分解

小波包分解克服了小波分解时间分辨率与频域分辨率不能同时达到一定要求的缺陷,对低频和高频部分都进行了分解[7],并能根据最小代价函数求解原始信号的最佳分解路径[8]。

小波包分解时,相邻级数的小波函数与尺度函数具有递推关系,其表达式如下:

(6)

式中:μ—小波包,其上标表示级数,下标表示该级里的位置;hk—低通滤波器;gk—高通滤波器。

hk和gk的表达式如下:

(7)

式(6,7)经过整理可得:

(8)

无论是小波变换还是小波包变换,其中一个重要的环节是选择合适的小波函数基进行信号分解。常用的几类小波函数基有:

(1)Aubechies小波(dbN[9],N为小波分解级数)有较好的正则性,消失矩为N。随着N的增加,小波更光滑,时域紧支撑性降低,频域局部性增加,可分性更强。小波函数及尺度函数的支撑区间为2N-1(N=1)时,就是Haar小波;

(2)Haar小波[10],有紧支撑性及正交性,时域上不连续;

(3)Biorthogonal小波(Bior,即双正交小波[11])是对称的、紧支撑的,具有线性相位性,使用2个对偶的小波进行信号分解与信号重构;

(4)Mexican Hat小波[12]是高斯函数的二阶导数,因不存在尺度函数,所以不具备正交性;

(5)Symlets小波(symN[13],N为分解级数)是对dbN小波的一种改进,除了具备dbN小波所拥有的特性外,还具备更好的对称性,是一类近似对称的紧支撑正交小波。因此,symN小波能在一定程度上减少信号重构时产生的相位失真。symN小波的支撑区间长度为2N-1,消失矩为N。

要选择合适的小波函数基[14],除了要考虑支撑区间大小之外,还要考虑小波的对称性、正则性及消失矩。对称性保证了信号重构时不产生相位畸变,而正则性则保证了信号的光滑和可微性。针对大部分小波而言,正则性与消失矩之间是正相关的。

最后,要根据输入信号的波形,选择与其相似性高的小波,更易拟合及分解信号。通过观察采集的原始信号数据集特征,笔者最终选择Symlets小波作为小波函数基。

1.2.2 EMD经验模态分解

为了最大限度地去除噪声信号,保留有用的信号,笔者提出了一种二级降噪操作方法,即将小波包分解后所提取的分量作为原始数据,代入到经验模态分解的操作中,进行再次降噪。小波包分解都需要选定小波基,固定小波基必然会降低算法的适应性,而经验模态分解(EMD)可以克服基函数无自适应性的问题[15]。

EMD分解信号所得的各层分量称为内涵模态分量(intrinsic mode functions, IMF),IMF需要满足过零点及极值点个数之差小于等于1,且关于时间轴局部对称[16]。

原波形可分解为各层IMFs信号及余波之和。

2 实验验证

2.1 数据采集试验平台搭建

由式(5)可知,在轮式装载机铲掘作业时,需要采集的变量主要有:动臂油缸的大腔油压、小腔油压以及动臂举升角度数据。

(1)动臂大腔、小腔油压数据采集

装载机动臂大腔的压力值变化范围为0～20 MPa,因此,此处选择压力传感器参数为:0～40 MPa, M14,X1.5,FS0.2%;同时,由于动臂小腔的压力值变化范围为0～6 MPa,此处选择压力传感器参数为:0～25 MPa, M14,X1.5,FS0.2%。

装载机动臂大腔及小腔压力传感器安装位置如图3所示。

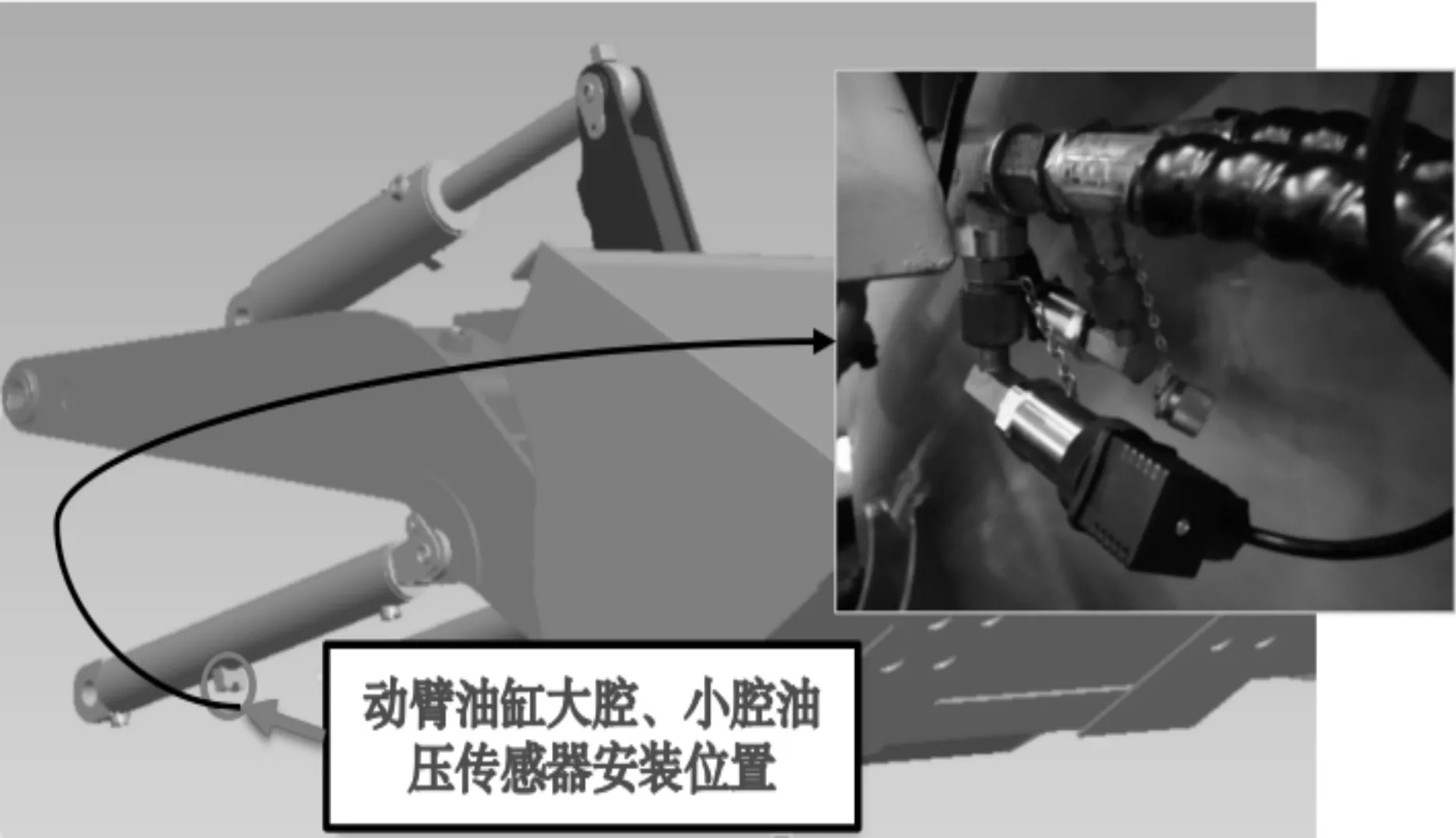
图3 装载机动臂大腔及小腔压力传感器安装位置

(2)动臂举升的角度数据采集

装载机作业时,笔者使用九轴角度传感器(蓝牙5.0)来采集动臂举升过程中X、Y、Z三轴的实时角度和角加速度。

角度传感器的安装位置如图4所示。

图4 角度传感器安装位置

(3)铲掘物料的实际重量数据采集

为了验证该动态称重方法的准确性,需要记录下每斗物料的实际重量,以用于误差分析。由于试验现场缺少大地磅,此处使用4个量程为5 T的小地磅替代,将装载机放置在地磅上进行称重,通过空斗及有物料两种状态的整车重量差,得到铲斗内物料的实际重量。

地磅及装载机称重图如图5所示。

图5 地磅及装载机称重图

2.2 数据处理

在铲掘过程中,根据动态称重方案,需要根据动臂及动臂油缸的实时举升角度,分析出举升近似匀速的区间,并以此截取动臂油缸的油压数据;然后,对该段数据采用小波包滤波及经验模态分解方式进行去噪;最后,将数据代入动力学模型公式进行求解。

装载机动态称重的具体流程如图6所示。

图6 装载机动态称重方案流程图

下文以重量为1.3 T的砝码称重时的数据为例,对数据处理过程进行详解。

(1)原始数据导入

在动态测量方案的实施过程中,需要实时采集动臂大腔油压、小腔油压、动臂举升角度Y1及动臂油缸举升角度Y2,如图7所示。

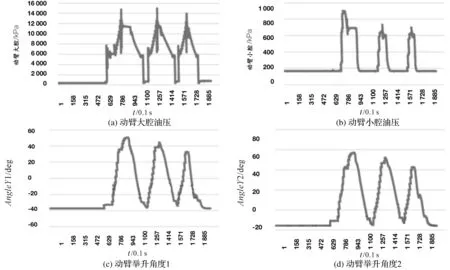
图7 砝码3次举升实时数据采集

(2)线性段区间数据提取

根据动臂举升角度,此处笔者选择趋于线性的段落区间,并以该区间截取相应动臂大腔、动臂小腔油压及动臂油缸角度数据。为了便于数据处理,笔者对所截取数据段的时间坐标轴进行统一调整,即截取的第一个数据点时间初始化为0,如图8所示。

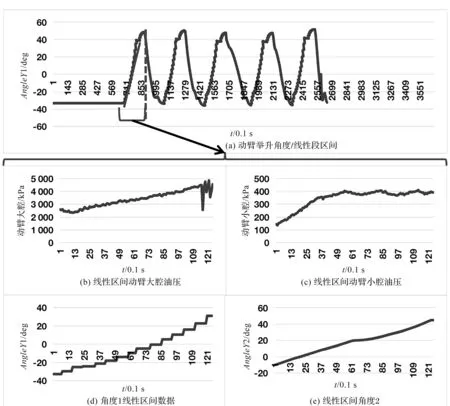
图8 动臂角度线性段对应区间的各种数据

(3)小波包分解与提取

根据采集的油压信号、角度信号,此处笔者选择与之相似的symN小波。为了得到平滑的降噪信号,基于MATLAB,笔者使用ddencmp()及wdencmp()函数进行默认的软阈值消噪操作,以解决因硬阈值函数导致小波域突变,使去噪后结果产生局部抖动问题;也可直接使用MATLAB工具箱WAVEMENU,选择小波基函数sym3,同时设置分解层数为2,对所提取的数据段进行小波包分解降噪。

最后输出的降噪信号如图9所示。

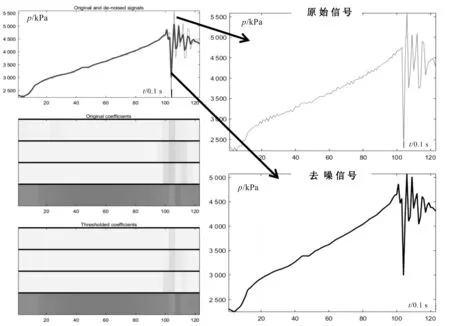
图9 小波包去噪前后信号对比图

(4)经验模态分解

笔者再次对小波包去噪信号进行经验模态分解操作,最后选取残余分量作为代入动力学模型的输入参数,如图10所示。

图10 经验模态分解的原始信号及残余分量

3 数据计算及结果分析

笔者采用厦工机械的某型号轮式装载机进行实车试验,使用四合一快换斗。

根据动力学模型公式,此处需要测量的常量如表1所示。

表1 实车测量的常量数据

在式(5)中,笔者分别代入经过区间截取与滤波降噪预处理前后的动臂及动臂油缸的实时角度数据,动臂大腔、小腔的油压数据以及所测量的常量,计算出空斗状态、砝码称重、铁矿砂称重、原生土称重时的斗内物料重量,并做出误差分析。

3.1 不同物料称重数据

正式进行物料称量前,装载机需要对铲斗空斗状态进行称重,得到对物料称重时的重量校准基数;随后,再对重量为1.3 T的标准砝码、随机铲装的一斗铁矿砂以及原生土进行称重。

空斗及3种物料称重视图如图11所示。

图11 空斗及3种物料称重视图

笔者采用多次测量空斗状态重量,并取平均的方法得到其称量时的修正基数。

空斗称重数据如表2所示。

表2 空斗称重数据(标定重量0.00 kg)

根据表2可知,基于本试验场地的装载机进行动态称重时,需要对最后的称重结果减去66.52 kg/36.43 kg进行修正。

实地试验结果,即砝码称重数据(标定重量1 300.00 kg)如表3所示。

表3 砝码称重数据(标定重量1 300.00 kg)

铁矿砂称重数据(标定重量1 198.00 kg)如表4所示。

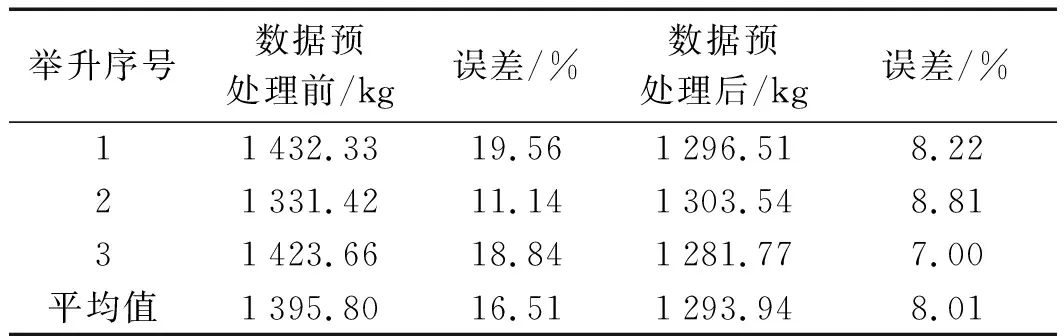
表4 铁矿砂称重数据(标定重量1 198.00 kg)

原生土称重数据(标定重量1 095.00 kg)如表5所示。

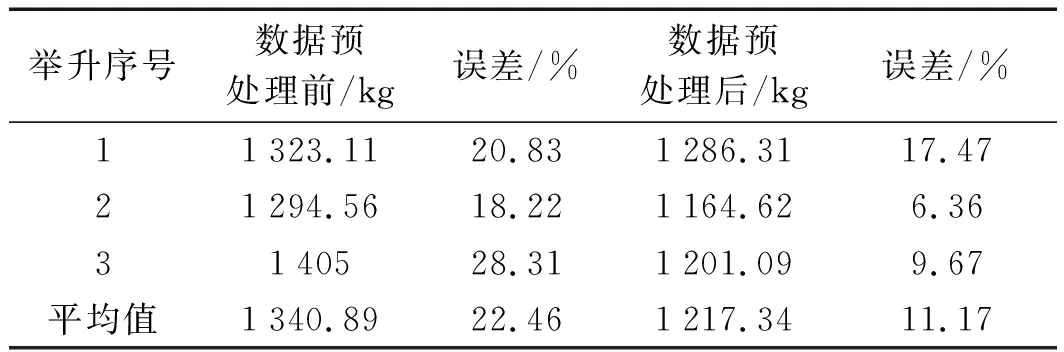
表5 原生土称重数据(标定重量1 095.00 kg)

3.2 结果分析

从对砝码、原生土、铁矿砂3种物料单次举升动态称重的数据分析可知,使用笔者所提出的二重降噪方法进行数据预处理前后,最小误差为对原生土的第二次举升,测量误差为6.36%;三次测量平均误差最小为对铁矿砂的称量,误差为8.01%。

该结果表明:该装载机动态称重方法以及其算法是有效的,线性段数据截取克服了铲装周期内数据段划分困难的局限性;同时,通过称重数据表中的数据对比,证明小波包结合经验模态分解的数据预处理明显提高了称重数据的准确性。

4 结束语

基于转动定律,笔者对某型号装载机铲掘作业的相关部件进行了动力学建模,通过合力矩分析得到了称重物料与动臂结构的油压、角度之间的映射关系;结合数据线性段截取技术,重点对实车试验数据进行小波包降噪结合经验模态分解的二级降噪预处理;最后,根据现场已有3种不同物料分别进行了实车试验。

研究结果表明:

(1)实车试验测量的最小误差为6.36%;

(2)单次铲装多次称重的平均误差最小为8.01%;

(3)在实际称重中,采用该动态称重数据处理方法可以显著降低称量误差,称量结果准确性高。

在后续的研究中,笔者拟增加试验数据,并结合大数据分析手段,对最终的称重结果进行补偿校准;同时,尝试采用其他的改进算法(如EEMD、ICEEMDAN等)来对数据进行降噪预处理,以进一步提高测量的精度。