基于蒙卡-点核积分耦合的核电厂退役辐射场计算

郭雨非，章航洲，刘水清，刘艳芳，吴 耀，王 力，肖 峰

(1.中国核动力研究设计院，成都 610005；2.四川省退役治理工程实验室，成都 610005)

在核电厂退役过程中，退役现场的放射性源项给人员防护和环境保护带来了难题，同时在强放射性水平的退役作业环境下，需对退役装备的耐辐照性能进行特殊的考虑。因此，退役现场的辐射场水平是影响退役策略、退役工艺决策的重要因素之一，同时也是开展辐射防护活动的主要依据之一[1-2]。确定辐射场水平有现场测量和理论计算两种手段，但现场测量给出的是退役作业特定状态下的测量结果，由于部分现场点的不可达性，造成现场测量存在较大局限性，而且强辐射场给工作人员造成很大辐射风险；而理论计算可以预测不同退役工况下的辐射场，还能给出全空间各点的辐射水平，解决了现场测量的时空局限问题，所以辐射场计算是确定辐射场水平的重要方法[3-4]。

在核电厂退役现场中，既存在几何简单的区域也存在几何复杂的区域，如结构较为简单的管道和结构错综复杂的压力容器内部；同时，退役过程中现场设备的数量、位置、放射性源项等都在不断变化，导致辐射场也在不断变化，因此需快速、准确地计算出辐射场[5-6]。而辐射场计算有三种基本方法：(1)离散纵标法：适用于求解几何简单的、三维可转化为一维或二维几何的问题；(2)点核积分法：半经验方法，计算速度快，但求解复杂几何问题时计算结果一般比真实值大1～2个数量级；(3)蒙特卡罗方法：概率论方法，计算时间长，适用于求解几何复杂的、没有厚屏蔽的问题。综上，三种基本方法各有优势和不足，单独使用无法满足快速、准确的计算要求。因此本文将分别适用于复杂几何和简单几何的蒙卡和点核积分方法耦合起来，形成蒙卡-点核积分耦合方法，并将其应用于秦山一期的退役辐射场计算。

1 蒙卡-点核积分耦合方法

1.1 方法研究

蒙卡-点核积分耦合方法的基本思想是：在几何复杂的区域使用蒙特卡罗方法求解，在几何简单的区域使用点核积分法求解，在耦合面上进行粒子参数的转换。基于此，将核电厂退役现场内的设备分为源项设备和屏蔽设备：源项设备是具有放射性源项的设备，如压力容器、堆内构件等；屏蔽设备是含有的放射性源项可以忽略的设备，可认为其仅具有屏蔽作用，如工艺房间墙体。设置一个包络面将所有源项设备包络起来，同时该包络面不会包络屏蔽设备或与屏蔽设备相交，如图1所示。该包络面即可作为耦合计算的耦合面，其内部即为蒙卡计算区域，外部即为点核计算区域。

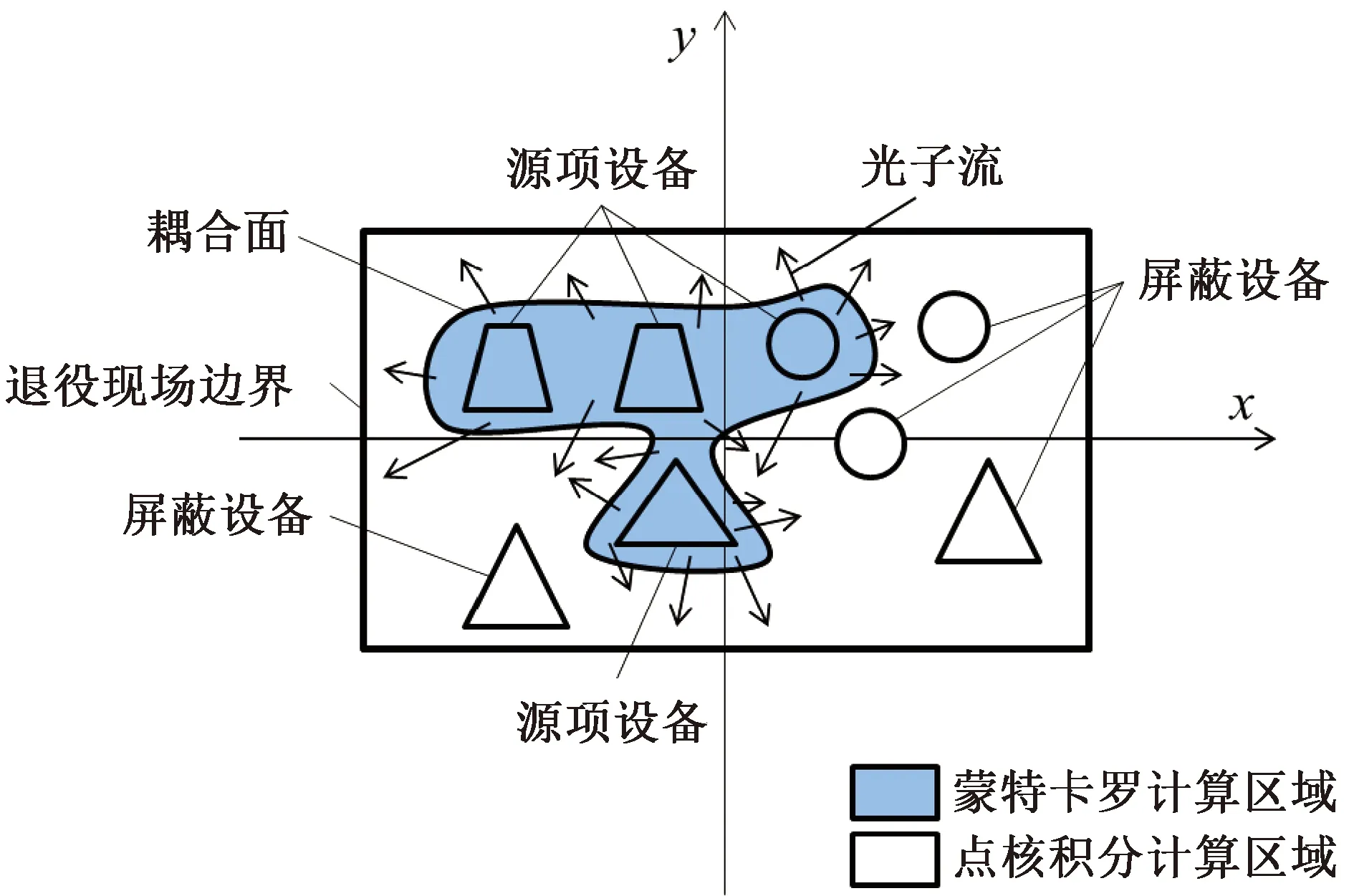
图1 核电厂退役现场计算区域划分Fig.1 Decommissioning site division for nuclear power plants

认为蒙卡区域是纯发射体，使用Boltzmann方程[7]可得：

(1)

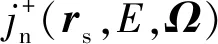
可以看出，耦合面外表面的γ光子流量率即点核区域的面源源项。由此可得耦合面上粒子参数的转换过程：

(1)首先对耦合面的外表面进行网格划分，得到离散面源；

(2)用蒙卡方法计算得到通过各个面源的γ光子流量率；

(3)再将每个面源等效转换为一个点源，其光子向耦合面外发射，放射性均匀分布于朝耦合面外的2π角范围内，其每秒发射的γ光子数等于该面源光子流量率、出射光子的能谱与从该面源出射光子一致、位置位于该面源中心，该点源即可作为点核积分计算的输入源项，如图2所示；

图2 耦合面面源转换为点源示意图Fig.2 The diagram for the coupling surface from surface sources to points sources

(4)用式(2)所示的点核积分公式[8]计算得到点源对空间各点的剂量率贡献；

(5)最后对所有点源的剂量率贡献求和，即可得到空间各点的剂量率。

(2)

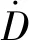
1.2 程序系统

针对蒙卡方法选用MCNP5程序及基于ENDF/B-Ⅵ的连续能量截面数据库进行。MCNP5是美国洛斯阿拉莫斯国家实验室开发的多功能通用蒙卡计算软件，由FORTRAN语言编制；使用了组合几何技术，可以使用一次、二次甚至四次曲面来描述三维几何结构，具有较强的几何通用性；提供了点源、面源和体源等多种源分布及相关参数，用户可灵活定义；提供了γ光子的6种基本计数，并留有修改计数的接口，可以满足用户的各种计数需求；减方差技巧比较齐全，用户界面也相对友好，是目前使用较为广泛的蒙卡计算程序。

针对点核积分法选用QAD-CG程序进行。QAD-CG程序由美国橡树岭国家实验室和洛斯阿拉莫斯国家实验室联合开发，使用数值积分方法来求解点核积分式。与MCNP5一样，QAD-CG也采用了组合几何技术，带有9种基本体元素，大大减少了输入几何模型所需的时间。

基于C#语言和窗体应用程序的形式，开发了蒙卡-点核积分耦合计算程序。可以根据用户输入，建立退役现场的辐射场计算几何模型；实现了对耦合面的选取，并通过调节参数对耦合面进行网格划分；并将MCNP5和QAD-CG耦合了起来，实现了两个软件之间的数据传递。

2 体源计算模型及计算

2.1 单体源计算模型及计算

2.1.1单体源计算模型建立

首先建立一个单体源的计算模型对耦合计算方法进行验证。如图3所示，单体源材料为波特兰水泥的圆柱形水泥固化，每秒发射1.0×106个γ光子、放射性均匀分布、能量1.33 MeV，体源位于一个屏蔽房间中；圆柱体源的底面中心坐标为(0,0,0)，半径150 cm，高200 cm；房间边界x=(-800～1 000)cm，y=(-800～800)cm，z=(0～300)cm；屏蔽墙位于x=(480～500)cm处，材料为普通混凝土。

图3 单体源计算模型Fig.3 The single source calculation model

2.1.2计算结果分析

在屏蔽墙外选取10个计算点，用耦合方法、蒙卡方法和点核方法分别进行计算，三种方法的计算结果及相对偏差列于表1。进行耦合计算时，耦合面设置为底面中心坐标(0,0,0)、半径150 cm、高200 cm的圆柱体。

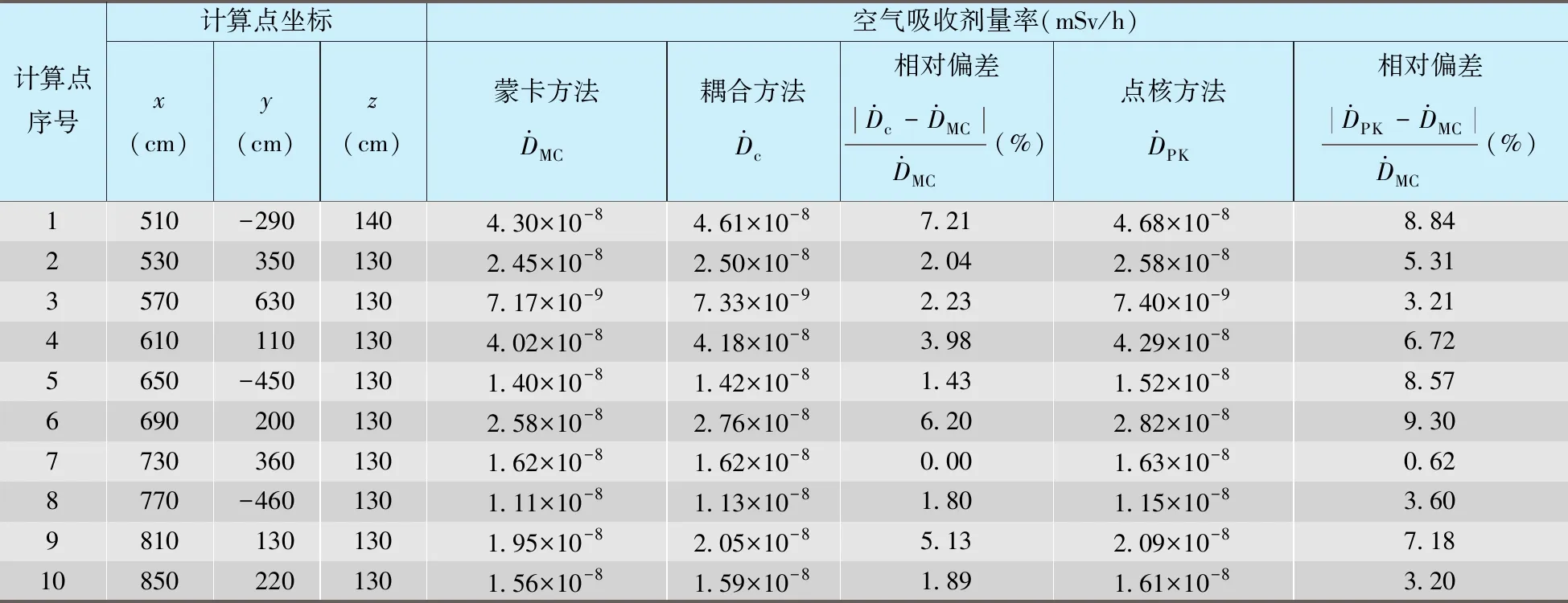
表1 单体源模型下耦合方法和单一方法的计算结果对比Tab.1 Comparison of calculation results of the coupling method and the single methods in the single source model

从表1 可以看出，对于选取的计算点，点核方法和蒙卡方法的计算结果较接近，相对偏差小于10%；耦合方法和蒙卡方法的计算结果也较接近，相对偏差也小于10%。这是由于单体源计算模型的几何简单、点核积分法适用造成的；受此影响，耦合计算结果也很接近蒙卡计算结果。同时可以注意到，对于选取的计算点，点核方法的计算结果均大于蒙卡方法的计算结果，这是因为点核积分使用的积累因子B是基于γ射线在无限均匀介质中的输运结果进行拟合得到的[9]，而实际上屏蔽体是有限体积的，在边界面上γ射线会发生反射，造成参考点处的实际剂量率较点核积分计算值偏小；屏蔽体厚度越大，输运至边界面的光子能量越小，反射越严重，点核积分法的计算偏差也就越大[10]。

在计算时间方面，在双核CPU、单核频率3.7 GHz、内存4 GB的个人计算机上，蒙卡方法用3 h得到了计算结果，统计误差均小于5%；而耦合方法用30 min完成了蒙卡部分的计算，统计误差小于1.5%，又用约10 min进行了点核部分的计算，计算速度提高了3.5倍。

综上，在单体源模型下，耦合方法相比于点核方法计算准确度没有太大优势，但相比于蒙卡方法具有计算时间短的优点。

2.2 多体源计算模型及计算

2.2.1多体源计算模型建立

在单体源模型的基础上增加一个圆柱体源，形成多体源计算模型，如图4 所示。增加的圆柱体源能量也为1.33 MeV，每秒发射1.0×106个γ光子，放射性均匀分布，材料也为波特兰水泥，底面中心坐标(-400，400，0)，半径150 cm，高200 cm。

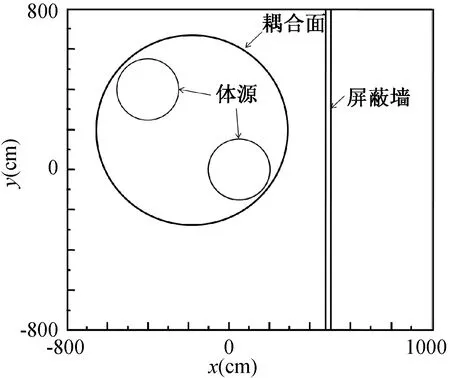
图4 多体源计算模型Fig.4 The multi-body source calculation model

2.2.2计算结果分析

计算点选取与单体源模型一致。由于QAD-CG程序无法计算多体源问题，因此本节仅用耦合方法和蒙卡方法进行计算，两种方法的计算结果及相对偏差列于表2。进行耦合计算时，耦合面设置为底面中心坐标(-200，200，0)、半径440 cm、高200 cm的圆柱体。

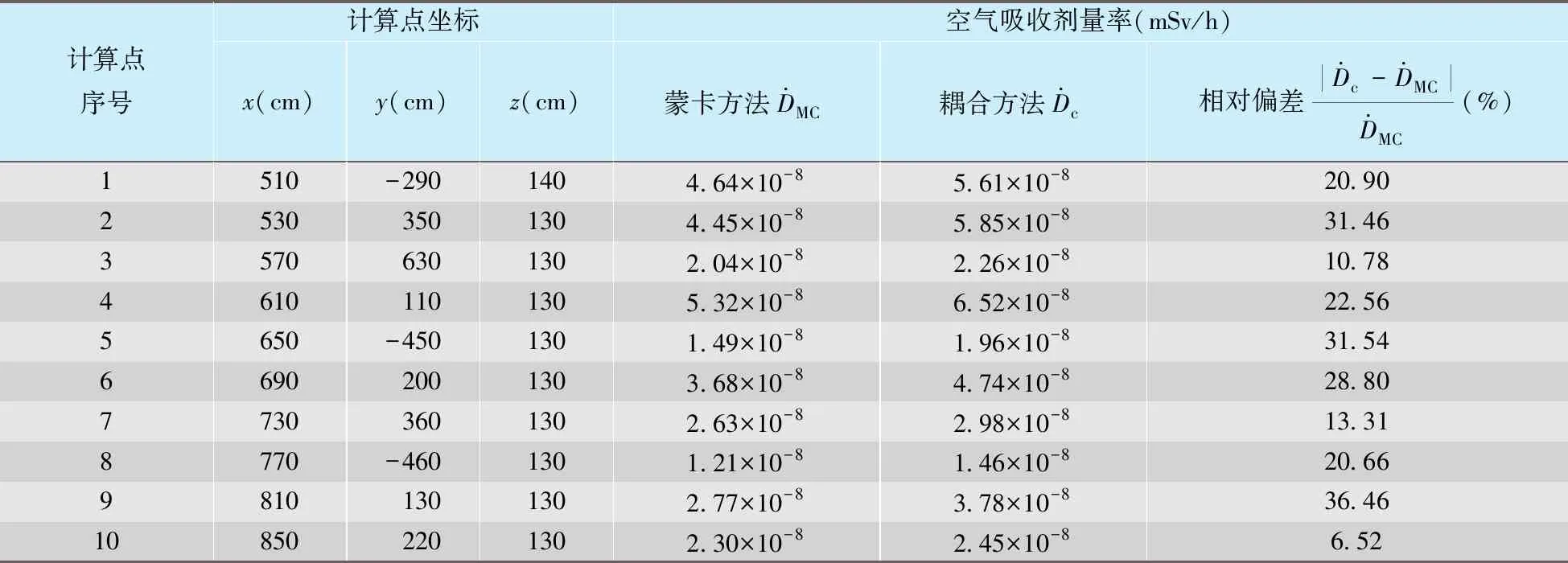
表2 多体源模型下耦合方法和蒙卡方法的计算结果对比Tab.2 Comparison of calculation results of the coupling method and the MC method in the multi-body source model

从表2可以看出，对于选取的计算点，耦合方法的计算结果与蒙卡方法相比最大可相差约36.46%，较单体源模型中的相对偏差明显增大。这是因为在将耦合面离散面源转换为点源的过程中(如图2所示)，实际通过耦合面的光子的出射方向是各向异性的，但对γ光子运动方向的转换仅考虑了相对耦合面向外，在点源发射光子的2π角范围内，光子出射方向是各向同性的，这样转换的等效性是不足的。在单体源模型中，耦合面即体源的外表面，造成耦合面上光子运动方向接近各向同性分布，因此单体源模型下耦合方法具有很高的计算准确度。但在多体源模型中，由于两个体源的互相屏蔽作用，输运到耦合面的γ光子的运动方向具有很大的各向异性，所以多体源模型下耦合方法的计算准确度有所降低。这个问题将在后续的研究中开展进一步的分析并加以改进。

在计算时间方面，与单体源模型相同的机器条件下，蒙卡方法用5小时得到了计算结果，统计误差均小于5%；而耦合方法用40 min完成了蒙卡部分的计算，统计误差小于1.5%，又用约22 min进行了点核部分的计算，计算时间仅为蒙卡方法的1/5。

因此，对于多体源辐射场计算问题，耦合方法的计算速度快，相对偏差小于1个数量级，可以认为计算准确度较高。

3 秦山一期退役辐射场计算

3.1 秦山一期计算模型

以秦山一期为例，将蒙卡-点核积分耦合方法应用于实际工程。不考虑燃料组件具有的放射性源项，对卸料后的秦山一期堆本体进行简化，简化后的模型如图5所示，包括压力容器顶盖、压力容器筒体、压力容器底盖、各内部构件等17个源项设备，内部构件从上到下依次为导向筒组件、压紧支撑结构、吊篮筒体、吊篮围板、下栅格板组件、防断组件。紧靠压力容器设置一个半径190 cm、高1 022 cm的圆柱面作为耦合面，耦合面内部是蒙卡计算区域，外部是点核积分计算区域。输入源项为2018年大修后的活化源项[11]，纳入本次计算的放射性核素主要包括52V、51Cr、54Mn、56Mn、59Fe、58Co、60Co、65Ni等γ射线能量高、分支比高的核素；根据文献[11]，本计算模型的放射性主要分布于吊篮围板，其放射性活度占总放射性活度的90%以上。该计算在14核CPU、单核频率2.4 GHz、内存64 GB的工作站上进行。

3.2 计算结果分析

在秦山一期计算模型中选取4个计算点，如图5所示。其中，1号点位于压力容器最高点上方1 m处；2～4号点距压力容器侧面20 cm，点间距为150 cm。耦合方法和蒙卡方法的计算结果及相对偏差列于表3。由表3可以看出，所有计算点两种方法的计算结果相差不超过一个数量级，大部分计算点相差不超过100%，准确度符合工程应用要求。其中，2号点和4号点的相对偏差和多体源模型下的相对偏差相当，这是由于秦山一期模型内多个体源的互相屏蔽作用造成的；但在1号点处，相对偏差达到200%，远远高于其余3个点，这不仅仅是因为模型内多个体源的互相屏蔽作用，还因为1号点正对的压力容器顶盖具有半球形外形，而1号点正对的耦合面又是一个平面，由于几何面的变化，输运到上部耦合面的γ光子的运动方向具有很强的各向异性，所以在1号点处耦合方法的计算偏差较大；而3号点正对放射性活度占比90%以上的吊篮围板，由于发射的γ光子能量高、数量多，输运至3号点附近耦合面时，光子运动方向接近各向同性分布，因此3号点处耦合方法的计算准确度很高。由此可以得出，计算模型中各体源的互相屏蔽情况、耦合面和模型外表面的契合程度、放射性活度的分布情况，都会对耦合方法的计算准确度产生影响。

图5 秦山一期简化模型Fig.5 The simplified model of Qinshan Phase I

表3 秦山一期计算模型下耦合方法和蒙卡方法的计算结果对比Tab.3 Comparison of calculation results of the coupling method and the MC method in the calculation model of Qinshan Phase Ⅰ

在计算时间方面，蒙卡方法的计算时间为8小时，统计误差小于5%；而耦合方法用2小时完成了蒙卡部分的计算，又用约5分钟完成了点核部分的计算，计算速度提高了约3倍。

综上，蒙卡-点核积分耦合方法的计算准确度和速度均满足要求，可以解决核电厂退役辐射场计算中的几何、更新问题。

4 结论

本文从核电厂退役对辐射场计算速度和准确度的要求出发，结合核电厂退役现场的空间特点，提出了蒙卡-点核积分耦合方法。首先用耦合方法和单一方法分别计算了单体源模型的三维辐射场，结果表明耦合方法对于单体源模型在计算准确度上没有明显优势，但计算速度相比于蒙卡方法却提高了3.5倍。然后建立了多体源计算模型，结果表明耦合方法结合了蒙卡和点核积分两者的优点，计算准确度较高，同时计算时间短，可以应用于多体源问题的辐射场计算。但发现多体源模型的计算结果偏差高于单体源模型结果偏差，还发现了耦合方法对光子运动方向的转换不够等效的问题。

针对秦山一期的堆本体建立了简化模型，并用耦合方法和蒙卡方法分别进行了计算，结果相差不超过1个数量级，满足工程应用要求，但在不同点位处相差较大，相对偏差最小为1.25%，最大可达202.74%，进一步分析得出，造成该现象的因素包括计算模型中各体源的互相屏蔽情况、耦合面和模型外表面的契合程度以及放射性活度的分布情况。因此，虽然耦合方法对核电厂退役辐射场计算上的适用性得到了验证，但后续还需要对光子运动方向转换方法、耦合面选取方法进行研究和改进，以便基于耦合计算程序开发核电厂退役仿真系统中的辐射场计算模块，为退役方案研究提供计算分析手段。