AKAZE结合自适应局部仿射匹配的视差图像特征匹配算法

朱代先，吴 栋，刘树林，刘凌志

（1.西安科技大学 通信与信息工程学院，陕西 西安 710054；2.西安科技大学 电气与控制工程学院，陕西 西安 710054）

引言

视差是指从有一定距离的两个点上观察同一目标时产生的方向上的差异[1]。在实际中相机对同一物体进行拍摄的过程中，由于相机的平移运动，使得被拍摄的物体在不同视点中的成像位置不同，即产生了视差。在相机拍摄过程中，相机往往存在着平移、旋转、镜头缩放等运动，这就使得对同一物体拍摄的两幅照片存在视角、尺度、旋转等变化，我们称之为较大视差图像，由于视差图像重叠区域往往会存在纹理较少、特征不足的情况，这就使得视差图像的特征匹配变得更为困难。

图像的特征匹配是图像处理中的关键一环，用来建立两幅图像间的对应关系，例如运动中恢复结构[2]、同时定位与建图[3-4]、三维重建[5]等应用。目前基于点特征的图像特征匹配算法有的专注运算速度上的提升，代表算法有ORB(oriented FAST and rotated BRIEF)[6]算法以及BRISK(binary robust invariant scalable keypoint)[7]算法等，以求达到实时性，采用ORB 算法进行特征匹配，对于纹理丰富、视差较小的两幅图像，速度快且鲁棒性好，被广泛应用于同步定位与地图构建(SLAM)中，但是没有解决尺度不变性问题；有的专注于精度上的提升，代表算法有SURF(speeded up robust features)[8]算法，SURF 算法在保持SIFT(scale-invariant feature transform)算法优良性能的同时有效提高了计算速度，但容易造成边界模糊和细节丢失。

由于视差图像具有较大的深度差异，再加上复杂的相机运动，这就使得上述算法对视差图像特征匹配的鲁棒性不是很好，仅依赖描述符很难区分正确和错误匹配，正确和错误匹配点的筛选是视差图像特征匹配中的关键，也是视差图像配准中的关键。因此柳长安等[9]提出一种基于网格运动统计的自适应图像特征匹配算法结合GMS(grid-based motion statistics)[10]和随机抽样一致算法（random sample consensus，RANSAC）[11]做误匹配剔除，从而得到精确匹配点，但是由于ORB 特征的局限性使得算法对大尺度视角变换和旋转变换的效果不是很理想。杨璇璇等[12]提出一种井下巷道大视差图像拼接算法，采用基于多平面进行特征匹配点分组的方法，计算多个平面的单应矩阵，能较好地完成井下巷道大视差图像拼接的任务。Cavalli等[13]提出一种基于自适应局部仿射匹配的外点滤除算法，基于图像的仿射变换可以提供较强的几何约束，根据仿射变换通过RANSAC 滤除特征点对中的外点，效果较好。受多平面特征点分组方法的启发，本文提出一种AKAZE结合自适应局部仿射匹配的特征匹配算法，从具有较大视差图像提取特征点并进行匹配得到粗匹配点，接着根据自适应局部仿射匹配区分正确与错误匹配点。

1 本文算法

本文将AKAZE(accelerated-KAZE)算法和自适应局部仿射匹配算法结合，提出了一种视差图像的特征匹配算法，其流程如图1所示。

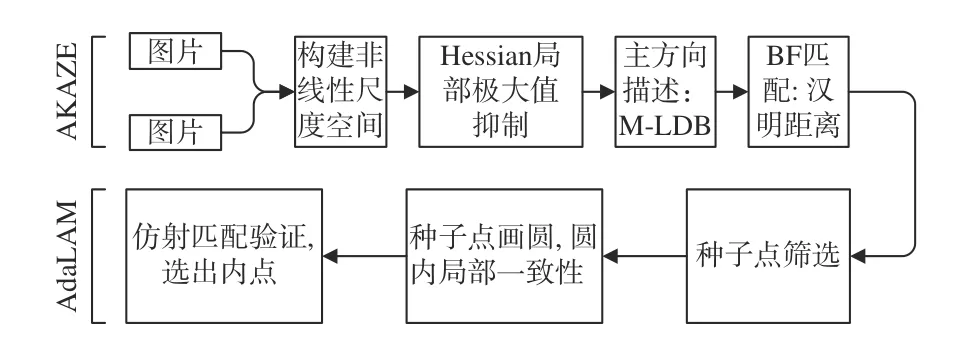
图1 本文算法流程Fig.1 Flow chart of proposed algorithm

该算法利用AKAZE 算法在旋转不变性、光照不变性、速度及稳定性等方面的优势[14]，对输入的两幅具有视差的图像提取特征点，在尺度空间保留更多特征信息，然后采用二进制描述符M-LDB[15]进行描述，并进行暴力匹配，生成粗匹配点对，对具有较大视差图像提取特征时，由于单个特征点的相似性，会存在大量近似的特征点，导致在特征匹配时出现大量的误匹配点对。针对粗匹配点对采用自适应局部仿射验证剔除误匹配，选取粗匹配点对中置信度好且分布均匀的点对作为种子点，并且在种子点周围画圆，在圆内通过自适应局部仿射匹配剔除误匹配点对，达到精细匹配的效果。

1.1 非线性尺度空间构建

非线性滤波构建尺度空间后图片会损失一些细节，但能够保留边缘信息，将尺度空间中更多的特征信息保留。图像亮度的扩散过程采用偏微分方程表达，表示为

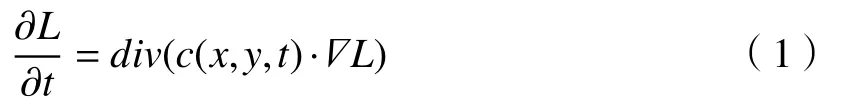
式中：div和分别表示散度函数与梯度算子；L表示图像亮度；时间t是尺度参数；c(x,y,t)表示梯度的函数，扩散能够适应局部图像结构。

在AKAZE 算法中，使用FED(fast explicit diffusion)算法求解非线性偏微分方程，进一步提升计算速度和算法实时性，并构建金字塔型尺度空间，寻找局部极大值点作为特征点位置，在特征点位置采用M-LDB(modified-local difference binary)描述符进行描述。

1.2 二进制描述符

M-LDB 以特征点为中心划分出n×n网格，在网格内通过特征的尺度进行离散点采样获得离散点的亮度值和水平、垂直方向的微分平均值，这些运算符是由0 和1 构成的二值描述符，其之间的距离采用汉明距离计算，可缩短计算时间从而进一步提高算法的实时性能。

1.3 匹配点精匹配

自适应局部仿射匹配算法（adaptive locallyaffine matching，AdaLAM），有效利用了现代并行加速硬件GPU，能够产生速度快且非常准确的离群点滤波器。AdaLAM 的核心思想如下：观测场景中3D 点都落在同一平面上，两张图片观测同一平面，则可以通过单应矩阵（homography）描述两幅图像中观测到的平面的映射关系，这个映射关系可以利用局部仿射变换[16]（affine transformation）A去近似。由于仿射变换具有良好的几何约束，利用几何约束可以滤除错误的匹配。

AdaLAM 算法步骤如下：

1）选择置信度高且分布较好的匹配点作为种子点；

2）以种子点为中心，在种子点近邻的匹配点认为具有局部一致性；

3）对于每一个种子点的近邻，用局部仿射变换验证一致性，最后保留那些局部一致较好的匹配点（认为是内点）。

种子点选择是假设一组特征点有较高的置信度分数，可以在局部采用仿射变换去局部逼近适应。对匹配好的特征点且置信度分数较高的，以R 为半径在圆内做局部极大值抑制，其中置信度分数由ratio-test[17]给出，如果在圆内这个特征点为极大值，那么将会被认为是种子点，从而确保种子点的独立性和覆盖范围。这一过程使用GPU 进行加速。

式中：EHo是具有均匀分散的异常值对应的假设；正样本计数P为对应假设匹配关系k最坏情况下的内联线数。将半径R内 的残差值映射到ck可以有效度量实际发现的内联点与仅在离群点假设EHo下发现的内联线数之比。当置信度大于固定阈值时，表示该模型对该匹配关系被拟合得较好，视该匹配被视为内点。每次迭代需要更新上述残差、置信度以及内点，后一次利用前一次得到的内点去拟合新的仿射矩阵，然后做校验，直至达到最大迭代次数，最后输出内点。

2 实验与结果分析

2.1 实验环境

本文算法实验环境如下：Intel core i7-8700K/3.7 GHz CPU，Ubuntu18.04 操作系统，16 GB 内存，编程语言为python，在VS code 中运行。

2.2 匹配结果对比实验

为了验证本算法针对视差图像特征匹配的优越性，从Oxford VGG 数据集中选取了4 组不同类型即视角变化（wall）、尺度与旋转变化（bark）、亮度变化（leuven）、模糊变化（bick）图像，4 组图像的像素分别为880×680、765×512、900×600、1 000×700，每组中有6 张变化程度逐渐增强的图像，分别采用SIFT+RANSAC、SURF+RANSAC、ORB+RANSAC、GMS、本文算法对每组图像中的第1 幅和第6 幅即变化程度最强烈的两幅图像进行特征点的提取和匹配，并计算特征匹配点对正确个数（内点）及算法运行时间，正确匹配点个数越多、用时越短，说明匹配效果越好。

图2 是选取Oxford VGG 数据集中wall 图像进行匹配，即视角变化的结果；图3 是该数据集中bark 图像进行匹配，即尺度与旋转变化的结果。

图2 视角变化图像匹配结果Fig.2 Image matching results of view-angle change

图3 尺度与旋转变化图像匹配结果Fig.3 Image matching results of scale and rotation change

由图2 可以看出，SIFT 和SURF 提取的匹配特征点较少，经过RANSAC 再次滤除外点后，依然有明显错误匹配。由图3 可以看出，SIFT 和SURF 针对尺度与旋转变化提取的匹配特征点经过RANSAC再次滤除外点后效果较好，但是SURF 相对于SIFT 提取的匹配点较少。由于ORB 特征本身不具备尺度和方向性，ORB 和GMS 算法针对图2 wall图像视角变化较大，针对图3 bark 图像尺度与旋转变化较大，基本无法匹配。本文算法针对视角变化、尺度与旋转变化提取的匹配特征点对，不仅匹配的特征点对数量较多，且特征分布均匀，针对有较大视差的图像匹配有较好的效果，取得较好效果的原因是由于AKAZE 算法对于视差图像存在的旋转、尺度变化鲁棒性较好，对于相似特征点之间的误匹配采用局部仿射匹配验证剔除了外点，从而提升了视差图像匹配的准确性。

图4 是选取Oxford VGG 数据集中leuven 图像进行匹配，即亮度变化的结果；图5 是该数据集中bikes 图像进行匹配，即模糊变化的结果。

图4 亮度变化图像匹配结果Fig.4 Image matching results of brightness change

图5 模糊变化图像匹配结果Fig.5 Image matching results of blurred change

由图4 和图5 可以看出，SIFT 和SURF 提取的匹配特征点，经过RANSAC 再次滤除外点后，效果远好于ORB 算法。GMS 算法通过降低特征提取阈值并采用网格运动统计剔除外点针对亮度变化和模糊变化效果较好，由图4（d）和图4（e）可以看出，GMS 算法在图像边角及汽车玻璃上的匹配点的特征点较少，但本文算法在这些区域都有分布均匀的匹配点，其与GMS 算法在亮度变化和模糊变化匹配效果上基本相当，但本文算法匹配点分布比GMS 算法均匀。表1 分别记录了SIFT、SURF、ORB、GMS 和本文算法在不同类型图像上的粗匹配点数和内点数。

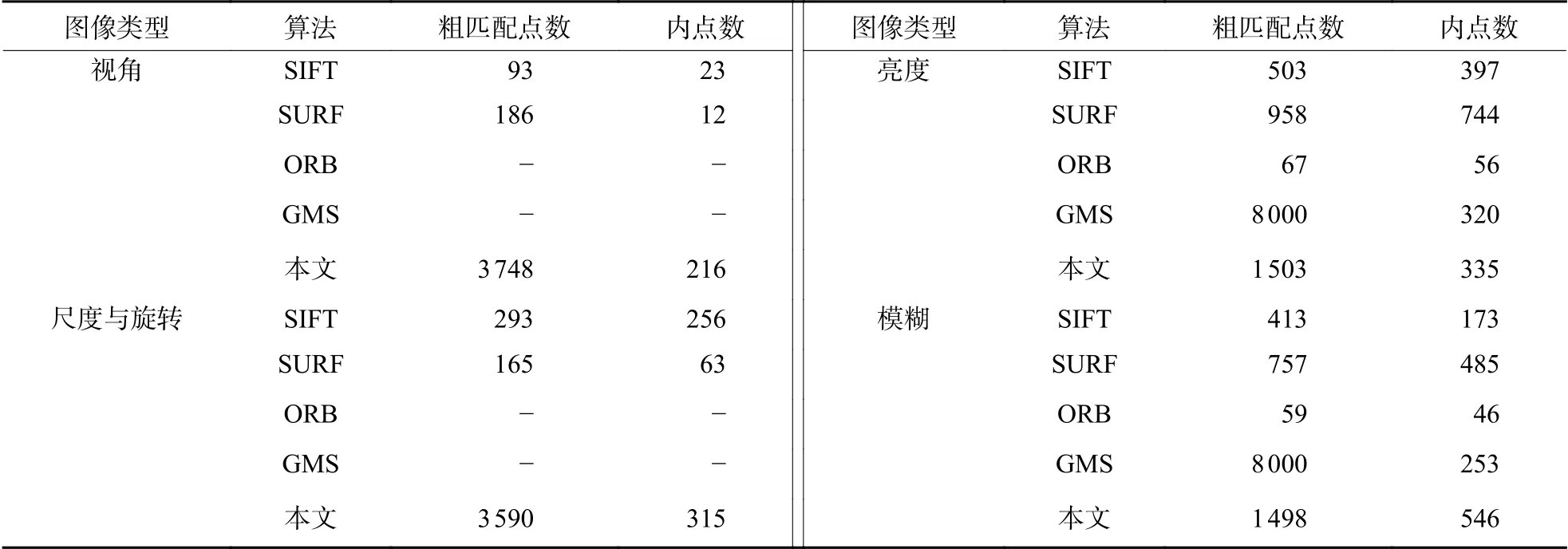
表1 特征匹配点统计Table 1 Feature matching points statistics

表2 分别记录了SIFT、SURF、ORB、GMS 和本文算法在不同类型图像上的特征提取粗匹配时间、外点滤除精匹配时间以及总用时。

表2 不同类型图像应用算法耗时Table 2 Time consuming algorithm for different types of images

从表2 中可以看出：本文算法主要在精匹配剔除误匹配外点耗时较长，而在特征提取匹配阶段由于非线性扩散方程的FED 解法和二进制描述子，相较于SIFT 和SURF 有优势；特征提取阶段ORB 算法用时最短；GMS 算法由于将特征提取阈值设置的特别低，导致提取的特征比本文算法高出两个数量级，故在特征提取匹配时，剔除误匹配阶段均耗时较长，但特征匹配效果以及针对不同类型图像匹配的效果不如本算法。本文算法在每组图像上的运行时间都相对比较均衡，在实时性方面本文算法还有待提高，需要继续优化。

2.3 实际应用效果

实际拍摄一组卡通狗的照片（分辨率为5 184×3 456像素），其纹理结构相似且同时存在尺度和旋转等变化，分别使用AKAZE 算法和本文算法匹配，结果如图6所示。

图6 实际应用结果Fig.6 Practical application results

由图6 可以看出：AKAZE 算法对于纹理相似且同时存在尺度和旋转变化的视差图像进行匹配明显存在大量误匹配点；本文算法是在AKAZE 算法的基础上结合AdaLAM 算法通过局部仿射匹配验证，剔除了大量相似特征点对，从而保证针对视差图像的特征匹配结果更好。

3 总结

本文提出了一种基于改进AKAZE 的具有视差图像特征匹配算法，针对视差图像容易同时存在由于尺度、旋转、视角的变化引起的特征点，容易产生误匹配的问题，采用AKAZE 算法提取特征并进行粗匹配，基于自适应仿射变换进行精细匹配。通过对比实验，结果表明，本文算法在图像存在视差或者发生尺度与旋转变化等不同场景下，本文算法提取特征点数量优于传统的特征匹配算法，可应用于从多视图几何恢复三维结构等需要对存在较大视差图像进行匹配的场景，本文算法的不足之处就是在精细匹配剔除误匹配阶段耗时较长，下一步将就如何提高算法的效率、缩短运行时间进行继续研究。