基于矢量光场的TeO2晶体旋光特性研究
郁步昭,王吉明,吴 彤,赫崇君,路元刚,刘友文
(1.南京航空航天大学 理学院应用物理系,江苏 南京 211106;2.南京航空航天大学 空间光电探测与感知工业和信息化部重点实验室,江苏 南京 211106)
引言
矢量光场一般是指波前平面上偏振态具有局域相异性的空间矢量结构光场,近20年来,获得了研究人员的广泛关注[1]。这类新型激光场在产生、传输、调控和与物质相互作用过程中,光场状态的时空演化区别于传统偏振光。最典型的一类矢量光场为柱对称矢量光场,其基本光场为径向偏振与角向偏振(也称方位偏振)场,2 种基本光场的行局域控制或叠加,可以获得更复杂、更具普遍性的柱对称偏振矢量光束、全庞加莱矢量光束或混合偏振态光束等。
二氧化碲(TeO2)晶体属正方晶系的单轴晶体,透光波段为0.33 μm~5.00 μm,具有双折射特性,在532 nm 波段no=2.599 8,ne=2.300 8。TeO2晶体经常用在声光调制中,近年来在中微子与暗物质研究、红外器件等方面也获得了深入研究和广泛应用[2]。同时,TeO2晶体也是一种自然旋光晶体,具有良好的旋光性,可用作旋光器件[3-5]。近些年来,关于包括矢量光场在内的涡旋光场或特殊结构光场经过单轴晶体等的研究逐步深入,如在各向异性晶体中发现的自旋-轨道霍尔效应等,各向异性晶体在矢量光场领域应用越来越广泛[6-9]。关于矢量光场经过旋光晶体的研究较少报道,本文基于旋光理论和矩阵传输理论,利用马赫曾德干涉方法和斯托克斯参量测量方法,对矢量光场经过TeO2晶体进行了旋光特性的研究,分析了TeO2晶体对径向偏振矢量光场的调控特征。
1 矢量光场的旋光测试光路与矩阵传输分析
旋光效应一般是指线偏振光在其间传播时偏振面发生旋转的效应,其旋光角与晶体的旋光率和晶体长度有关。根据旋光材料的螺旋结构分子感应理论,旋光特性取决于由回转张量G表征的晶体物质方程[10-11]

式中:回转张量G=Gs,其中G=gi,j,i,j=x,y,z,s为 沿光轴(z轴)传播的单位矢量,TeO2晶体的介电张量可以表征为

式中:ne与no为晶体的双折射率,g12=g21=g,可得到相应的圆双折射率为

晶体中波矢面旋转对称但在光轴处不接触,光轴附近波矢面偏离球面和椭球面,造成晶体沿光轴呈现旋光性,可以解释为线偏振光入射后发生圆双折射。设线偏振光分解的右旋和左旋圆偏振光的折射率分别为nr和nl,则旋光角度为2 个圆偏振光波相位差的一半,即

式中:d为晶体内传播距离;λ0为入射光真空中的波长。旋光率可定义为

在532 nm 附近,TeO2晶体的旋光率为143(°)·mm-1。
为研究矢量光束通过旋光晶体的特性,搭建如图1所示光路。光路采用马赫曾德尔干涉测量结构,产生矢量光场的为瑞典Arcoptix 公司的电控可变涡旋波片,该波片又称Q 波片,是一类广泛使用的矢量光场调控器件[12-16]。图1 中,532 nm 单纵模激光LD 通过可调衰减片后,进入空间滤波器进行准直扩束,再经过半波片来控制偏振分束器(PBS)分离光束的光强。主光路上透过晶体的光为水平方向偏振的线偏振光,参考光路上的光为竖直方向偏振的线偏振光。PBS 后方的半波片光轴调至45°,旋转偏振方向使其转换为竖直线偏振光。线偏振光经过Q 波片(拓扑荷q=0.5),在Q 波片处于调谐电压时(V=2.7 V),将入射线性偏振高斯光束转换成径向偏振光束。通过三维调整架精密调整TeO2晶体,使径向偏振光束沿晶体光轴(z轴)垂直射入晶体。晶体的透射光与竖直方向偏振的线偏振参考光在BS 中合束。合束后采用2 种测试方法,一种经CCD 记录线偏振光与柱对称矢量光场的干涉图像;另一种是通过λ/4波片和偏振片(虚框中所示),用CCD 进行全斯托克斯参量测量。
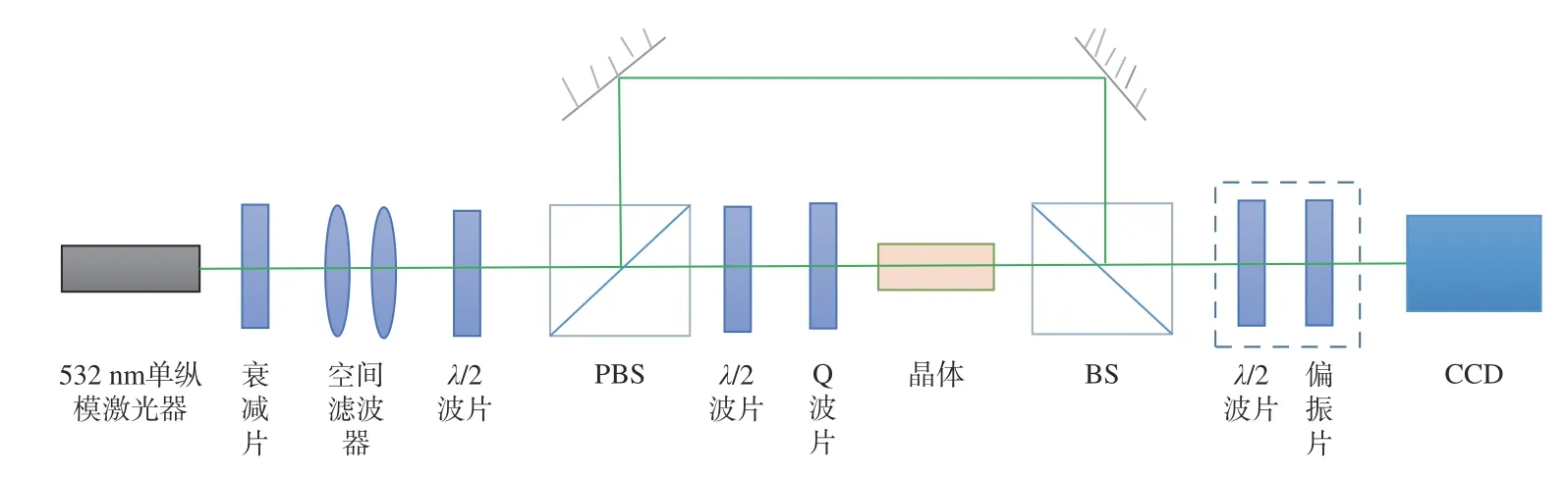
图1 基于马赫曾德尔干涉和斯托克斯参量测试的光路结构图Fig.1 Schematic of optical path based on Mach Zehnder interference and Stokes parameters measurement
利用Mueller 矩阵对矢量光场的旋光过程进行分析。设入射光为沿y轴的竖直线偏振光,其Mueller 矩阵为
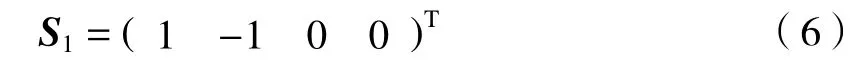
当Q 波片处于调谐状态时(φ=π),Q 波片的Muller 矩阵表示为[17]
当垂直线偏振经过调谐的Q 波片(q=1/2)后,出射光为径向偏振光

TeO2晶体的Muller 矩阵可表示为

当入射光为径向光时,出射光的Muller 矩阵可以表示为

可写成

式中:t1和 t2是常数,可以看出,从晶体出射的光束为柱对称矢量光束。与双λ/2波片的功能一致性进行比较,其Mueller 矩阵为[18]

式中:θ1与 θ2是2 个半波片快轴与入射偏振方向的夹角;Δθ为 θ1与 θ2之差,即2 个快轴间夹角。径向偏振光S2经过双半波片后偏振矩阵可表示为
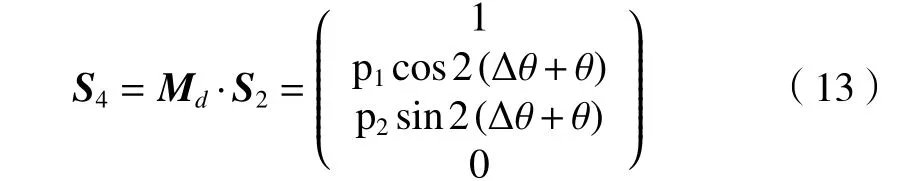
式中:p1和 p2是常数。可以看出,旋光晶体的旋光角 Φ即等效于双λ/2波片的夹角 Δθ。在实际研究过程中,由于光束发散角的影响,入射到晶体光束与光轴方向之间存在难以完全消除的傍轴误差,因此实际观测到的矢量光场存在局域线偏振度降低,即出现椭圆偏振光,此时的矢量光场可以表示为

式中:ε为偏振椭圆的椭偏度。
2 实验结果分析
530 nm 波长下TeO2晶体的旋光率为143(°)·mm-1,具有强旋光性,因而旋光角随晶体轴向长度变化非常敏感,0.1 mm 的变化就会导致近15°旋光角的变化。且随波长增大,旋光率会呈现非线性下降局势[11],532 nm 波长下旋光率会稍有变小。实验中选取了3 种尺寸的TeO2,分别为10 mm×10 mm×15 mm,10 mm×10 mm×20 mm 和10 mm×10 mm×50 mm。实验获得的干涉图如图2所示,其中图2(a)为不经过晶体直接干涉得到的条纹;图2(b)~(d)分别对应径向偏振光经过光轴向长度15 cm、20 mm 和50 mm的晶体后经干涉得到的条纹。可以看出,参考线偏振和径向偏振光干涉,径向光在和线偏振垂直方向上即水平方向发生退干涉现象,区域内干涉条纹变模糊,模糊中心轴线以虚线标出。该模糊区域的变化可用来判定旋光角度。通过比较图2 的旋光幅度,尤其是图2(d)中呈现的净90°旋光角,可得出旋

图2 矢量光场的马赫曾德尔干涉图Fig.2 Mach Zehnder interferogram of vector light field
光率为142.2(°)·mm-1,旋光周期(每旋光一圈为一个周期)为19.75。据此旋光率,计算15 mm 和20 mm晶体的旋光周期,分别为5.93 和7.90,净旋光角应分别为25°和36°,分析图2(b)和图2(c)可看出,图中干涉条纹模糊区域与无晶体情况相比,旋转角较小,都约在10°和20°附近。偏离计算理想值的原因主要是源于晶体长度的加工误差,设计加工的晶体长度偏离了理想值。在此实验基础之上,我们进一步增加了双波片调控实验,在晶体前插入了可旋转的双半波片,通过旋转双半波片,发现可以将图2(b)~(d)中扭曲旋转的干涉条纹调整至图2(a)的无晶体的干涉条纹,证实了矢量光场下TeO2晶体旋光效应等价于双半波片的作用。同时,可以借此通过双半波片的夹角度数来定量测定晶体的旋光角,与以上分析结果吻合。
使用干涉测量法,通过非相干区(模糊区)的旋转可以观察对偏振面的旋转。但由于非相干区存在一个范围,因此只能粗略定量判定旋光情况。为进一步较为直观地观察旋光特性及研究影响旋光特性的因素,遮挡参考光路,在主光路测量端进行全斯托克斯参数测量。在CCD 前增加将λ/4波片和线偏振片(图1 中虚框内部分),其中偏振片透光轴、波片快轴方向的方位角分别为 α 和 β,设I(α,β)为不同方位角下CCD 探测的光强分布,则4 种斯托克斯参量为[19-21]

式中:I(0°,0°)、I(90°,90°)为CCD 测得矢量场的水平和垂直偏振态分量的光强;I(45°,45°)、I(-45°,-45°)分别为对角线偏振态和反对角线偏振态的强度;I(0°,45°)、I(0°,-45°)分别为右旋(R)和左旋(L)圆偏振态的强度,通过4 个斯托克斯参量,可获得出输出光场的光强和偏振态分布。图3 为通过测试数据获得的输出光强分布及偏振态分布,其中图3(a)~(d)依次对应无晶体、10 mm×10 mm×15 mm、10 mm×10 mm×20 mm 及10 mm×10 mm×50 mm3 种尺寸晶体的情况。从图3(a)可以看出,在无晶体时,经Q 波片产生了径向偏振光。从偏振态图示可以看出,由于测试误差,在水平和竖直2 个特殊方向上偏振态不是很理想。图3(b)偏振态分布类似于图3(a),为径向偏振,但由于傍轴特性,根据(14)式,部分区域的线偏振退偏为椭圆偏振光。随着晶体变长,傍轴退偏特性越发明显,这一特征在图3(c)和图3(d)中尤其明显。根据前面干涉条纹分析,15 mm、20 mm 晶体透射光为柱对称矢量光场,偏离径向偏振仅在10°和20°左右,图3(b)和图3(c)中并不明显;50 mm 长晶体后旋光接近90°,图2(d)中矢量光场已转变为角向偏振光,与预期结果吻合。我们通过斯托克斯测量,不但进一步直观给出了TeO2晶体对矢量光场的旋光特性,还进一步证实了傍轴传播距离越长,引起的退偏振效应就越明显,如图3(c)和图3(d)中退偏就非常明显。


图3 全斯托克斯参量测试的强度与偏振态分布图Fig.3 Intensity and polarization state distribution of full Stokes parameters test
3 结论
本文通过Mueller 矩阵传输理论研究了TeO2晶体对径向偏振矢量光场的调控特征,在实验中,通过矢量光场干涉测量法和全斯托克斯参量测量法,分析了不同晶体样品的偏振态演化规律,揭示了TeO2晶体的旋光特性和退偏机理,表明其可以起到和双λ/2波片相同的偏振调控效果。研究结果有助于理解矢量光场在晶体中的传输特性,促进矢量光场相关晶体器件的设计与应用。

