基于高斯混合模型的液体电磁参数太赫兹测量方法

谢雨杉，黄 异，钟宇杰，罗曼婷，张政浩，林廷玲，钟舜聪

（福州大学 机械工程及自动化学院，福建 福州 350108）

引言

太赫兹时域光谱技术是一门自20世纪末发展起来的光谱技术，广泛应用于基础研究和工业领域，全球许多科研工作者致力于研究其在无损检测、化学分析、安全筛查等方面的潜在应用[1-4]。与红外光相比，太赫兹波的透射性很强，对大部分干燥、非金属、非极性材料都具有较好的穿透能力。

法国DUVILLARET 等学者提出了一种使用透射式太赫兹时域光谱快速可靠提取材料参数的方法，这种方法适用于大多数材料，使得透射式时域光谱技术被广泛地应用于精确测量固体样品的电磁参数和厚度[5-6]。但是对于在太赫兹波段不透明的材料，例如极性液体对太赫兹波具有强烈吸收、难以被其穿透的特性，若仍使用透射式时域光谱进行测量，须把样品制备得很薄，或注入被制备得很薄的器皿中，操作上存在一定的难度。反射式时域光谱测量此类样品可以避免这样的局限。但在反射式系统中，太赫兹波须经过更多的光学器件，信号传播光程更长，强度受到损失；且由于有一部分结构被暴露在密闭的样品室外，无法完全充满氮气，易受到环境中水蒸气的影响[7-8]；若没有恰当的信号处理，太赫兹信号的频谱将不可避免地产生变形或伪波动，引起电磁参数的振荡。

因此，本文针对反射式系统易受干扰引起的样品电磁参数振荡问题，提出一种使用高斯混合模型重新构建太赫兹时域光谱的方法，剔除了原始时域信号中的不相关信息，并通过理论模型成功提取出液体样品随频率变化的折射率及消光系数。

1 反射式液体电磁参数提取模型

1.1 反射式测量原理

如图1所示，待测液体放置在基底上方，基底由高阻硅制成，厚度为L，在测量波段具有恒定折射率n2。空气折射率为n1=1。太赫兹脉冲Ein以角度 θ1入射到基底底部。将来自空气-基底界面的反射脉冲Eref作为参考信号；来自样品-基底界面的反射脉冲Esam作为样品信号。

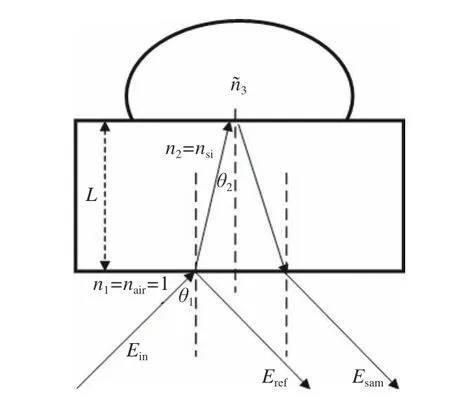
图1 反射式测量原理图Fig.1 Schematic diagram of reflected measurement

脉冲信号可由下式[9]表示：

1.2 基于高斯混合模型的太赫兹反射光谱重构

如前所述，使用反射式系统测量得到的信号易受到系统和环境的影响，影响了测量样品电磁参数的可靠性。本文提出一种恢复太赫兹信号的方法，反射信号可被表示为数学型式：

图2 Levenberg-Marquardt 算法流程图Fig.2 Flow chart of Levenberg-Marquardt algorithm

采用皮尔逊相关系数（pearson correlation coefficient）从数值角度验证信号恢复结果的优劣，记其符号为P，计算方法如公式（16）所示，系数越接近1，相关性越好，恢复效果越优。其中，Cov 为协方差，δ为标准差。

1.3 效果评价

2 基于时域有限积分的反射式太赫兹测量模型

使用基于时域有限积分算法的CST-MWS 对太赫兹波在样品中的传播过程进行建模。图3 表示了仿真模型的几何结构，基底到波导端口的距离为L1，厚度为L2，折射率为n。采用高斯脉冲作为激励源，边界条件设置为完美匹配层。

图3 CST 仿真模型Fig.3 CST simulation model

设置基底层的材料为Si；考虑到液体对电磁能量的吸收，采用（20）式所示的德拜方程来描述样品层介电特性[13]。介电参数如表1所示，其中εs、 ε∞、ε2分别为静态、光频、中间介电常数，τD、 τ2分别为慢、快弛豫时间。图4 示出了仿真得到的时域信号，提取2 个反射峰之间对应的时间延迟 Δt为11.55 ps，与（19）式计算的理论值11.49 ps 基本一致。

表1 德拜模型参数Table 1 Debye model parameters

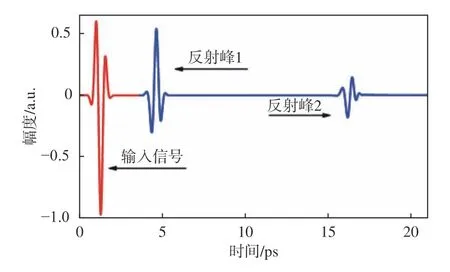
图4 仿真时域信号Fig.4 Simulated time-domain signal

根据1.1 节中介绍的模型计算得到样品的电磁参数如图5所示。结果表明，材料复折射率的实部与虚部均随频率的增大而减小，该现象被称为反常色散，由极化反应引起[14]。结果与实际基本一致，RMSE 在1 %以下，误差主要来源于时域有限积分算法本身的误差，说明了理论公式的正确性。

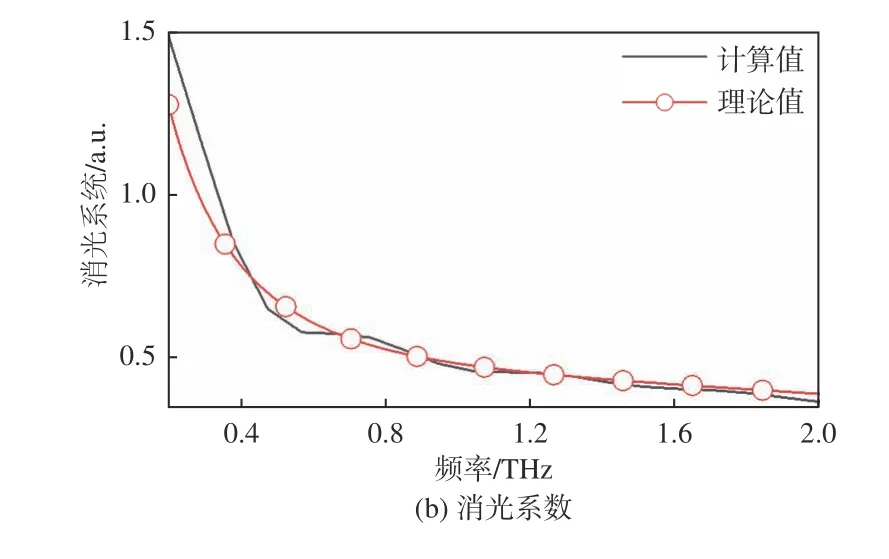
图5 水的复折射率Fig.5 Complex refractive index of water

3 实验验证与结果分析

3.1 太赫兹实验系统

实验所使用的太赫兹时域光谱系统及光路如图6所示。这套系统包含用于系统控制的集成电脑、封闭式光学系统及测量模块。采用飞秒光纤激光器作为激励源，激光脉冲经分束镜后分为泵浦光和探测光，泵浦光聚焦在发射极上产生太赫兹脉冲，频率范围为0.1 THz～4 THz，太赫兹脉冲经抛物镜聚焦于样品，经反射后由另一面抛物镜发送至探测器。

图6 测量系统Fig.6 Measurement system

3.2 结果与分析

图7 显示了测得的空硅片和盛有水的硅片的时域光谱，出现了2 个反射峰，与模拟结果一致。当硅片表面覆有水时，第2 个反射峰衰减较大，这是由于水对太赫兹波具有强烈的吸收。根据1.1节计算得到水的复折射率，得到的结果与文献[15]中报道的结果基本一致，如图8所示。

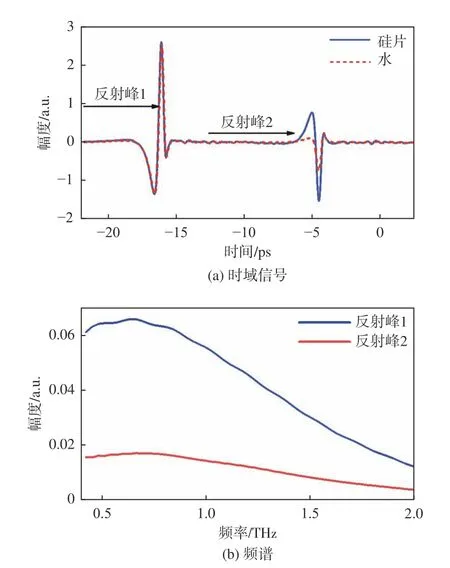
图7 空硅片与覆有待测液体硅片的测量结果Fig.7 Measuring results of empty silicon wafer and silicon wafer with liquid sample

图8 水的复折射率Fig.8 Complex refractive index of water

由结果看出，样品的电磁参数存在振荡现象。为解决这个问题，使用1.2 节中的方法对时域光谱进行恢复，图9 和图10 分别绘制了2 种样品的时域光谱及其恢复迭代过程。迭代完成后，时域中不相关的波动均被去除，恢复信号与原始信号的Pearson 相关系数分别为0.993 8、0.998 6、0.998 3、0.999 6，均在0.99 以上，说明本方法能够有效地对太赫兹时域波形进行恢复。

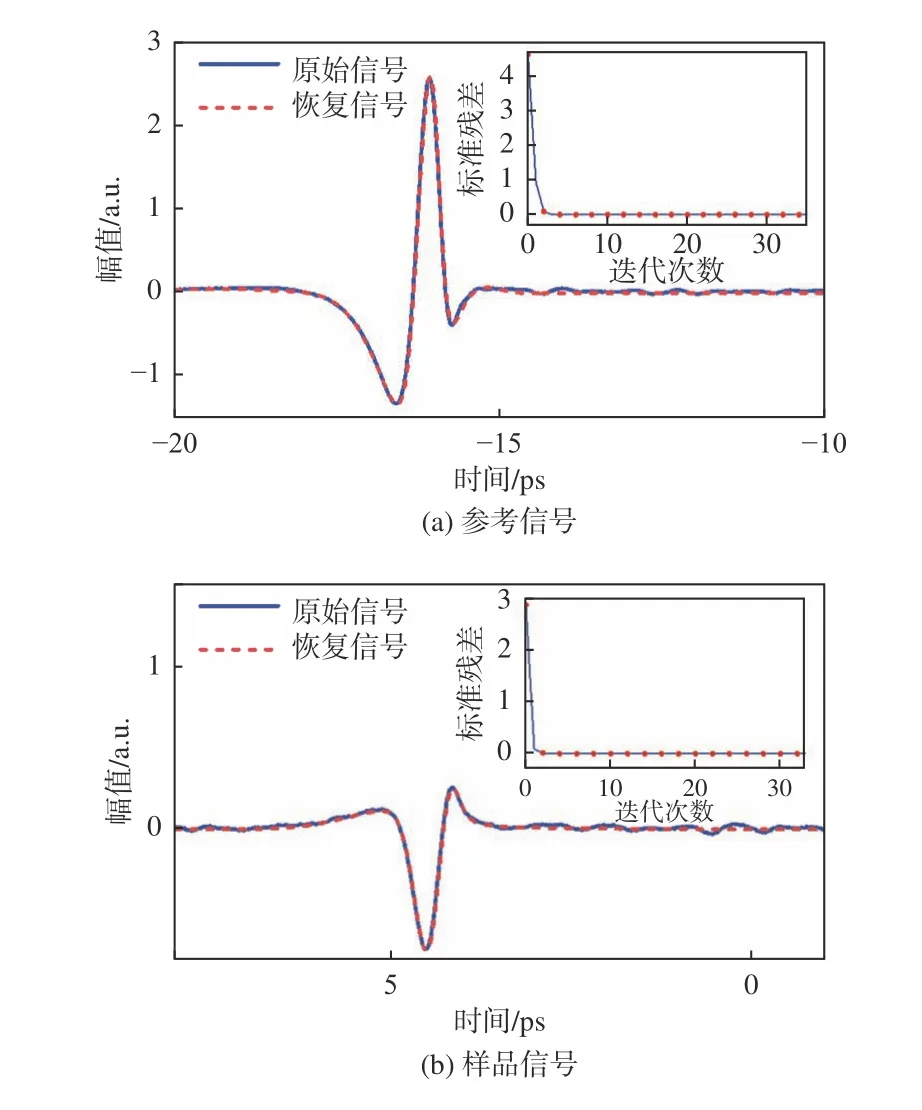
图9 时域信号恢复结果（水），插图为迭代过程Fig.9 Results of time-domain signal recovery(water),illustration is iterative process

图10 时域信号恢复结果（液体石蜡），插图为迭代过程Fig.10 Results of time-domain signal recovery(liquid paraffin),illustration is iterative process

图11 描述了分别从恢复信号与原始信号中提取的待测样品电磁参数。结果表明，2 种样品的电磁参数均在一定程度上消除了振荡。如图12所示，对其做DFA 分析可以发现，水的折射率和消光系数较之原始值，α标度指数分别上升了7%和3%；液体石蜡则分别上升了29%和31%。

图11 水和液体石蜡的复折射率Fig.11 Complex refractive index of water and liquid paraffin

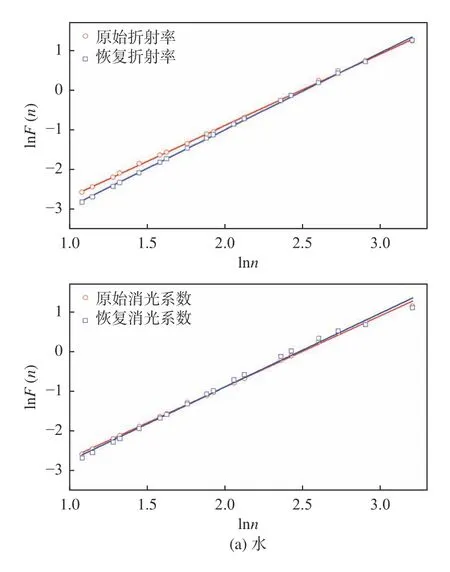
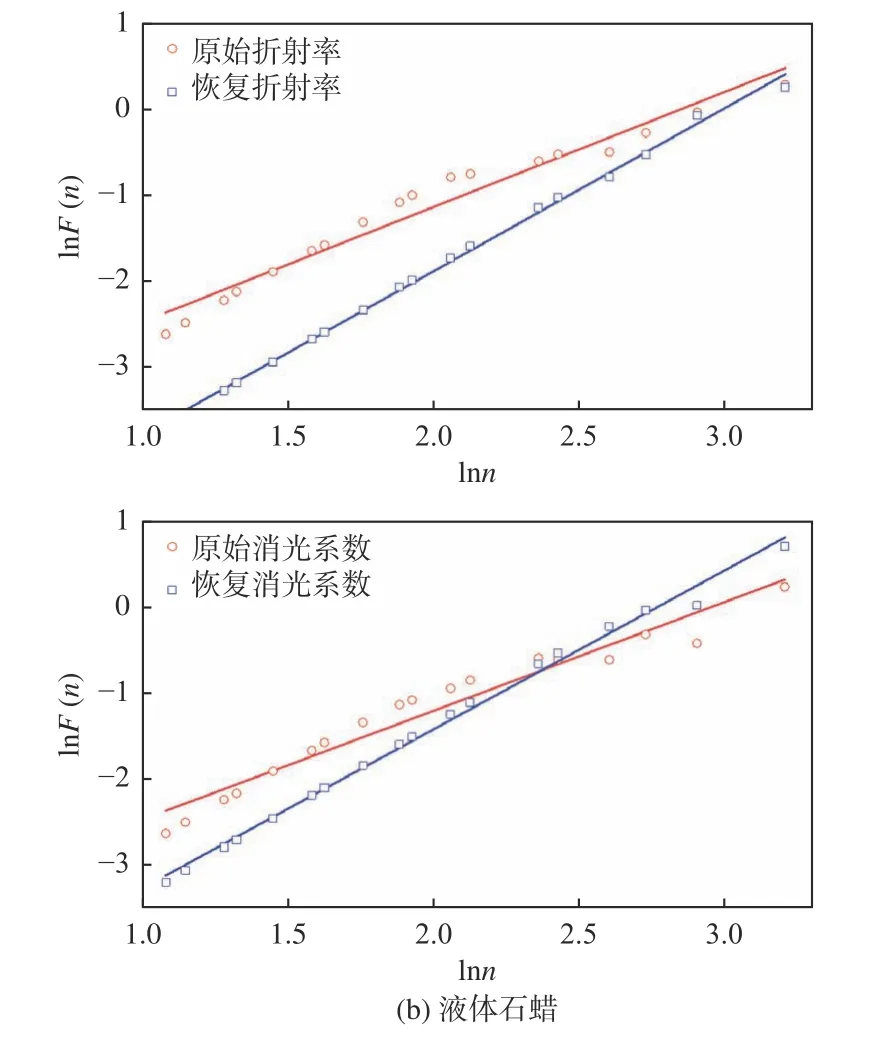
图12 去趋势波动分析Fig.12 Detrended fluctuation analysis

4 结论

由于极性液体会对太赫兹时域信号产生强烈吸收，本研究使用反射式时域光谱技术对液体样品进行测量，并针对反射式系统信号质量较差致使样品分析中电磁参数出现振荡的现象，提出一种基于高斯混合模型的信号恢复方法，该方法成功消除了太赫兹时域光谱中不相关的噪声信号。研究结果表明，使用恢复后的太赫兹信号计算得到的液体电磁参数，有效地消除了波动，验证了该方法在实际测量中的可行性。