路与几类图的Cartesian 积的邻点扩展和可区别全染色

王国兴

(1. 兰州财经大学丝绸之路经济研究院，兰州 730020; 2. 兰州财经大学信息工程学院，兰州 730020)

1 引言

本文中仅考虑有限、无向简单图.设G= (V,E)表示顶点集为V，边集为E的简单图.对任意x ∈V(G), N(x) ={y ∈(G)|xy ∈E}表示顶点x的邻集.此外，用Pn, Cn, Kn和Wn分别表示n个点的路、圈、完全图和轮.

图G的一个k-全染色是k种颜色1,2,··· ,k在图G的所有顶点及边上的一个分配.设f是图G的一个k-全染色，对任意的x ∈V(G)，称

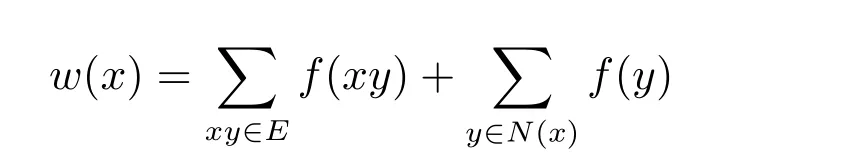
为点x的扩展和.图G的一个k-全染色f满足对任意的xy ∈E(G)，有w(x)/=w(y)，则称f是邻点扩展和可区别的(简记为NESD).使得图G存在NESDk-全染色的k的最小值被称为图G的邻点扩展和可区别全色数，简记为egndi∑(G).

Kalkowski 等人[1]引入并研究了图的邻和可区别一般边染色.Przybylo 和Wo´znizk[2]进一步提出邻和可区别一般全染色的概念，该问题的相关研究见文献[3-6].Flandrin 等人[7]在此基础上提出邻点扩展和可区别全染色，并对一些特殊图类：路、圈、完全图、树等进行了研究.同时，他们提出了如下猜想：

猜测1(NESDTC 猜想)[7]任意一个图的邻点扩展和可区别全色数不超过2.

图G与图H的Cartesian 积(或称卡氏积)记为G□H，其中V(G□H) =V(G)×V(H),(x1,x2)(y1,y2)∈E(G□H)，当且仅当x1y1∈E(G)且x2=y2，或者x2y2∈E(H)且x1=y1.

例如，路P5与P3的Cartesian 积P5□P3，如图1 所示.

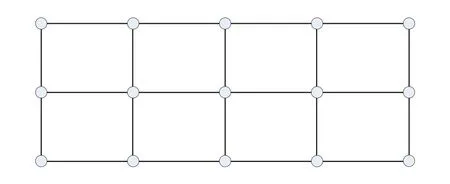
图1 Cartesian 积P5□P3

本文通过对Cartesian 积的结构进行分析，应用构造染色模式的方法证明了Cartesian积：Pm□Cn, Pm□Wn, Pm□Kn的邻点扩展和可区别全色数均为2.说明文献[1]提出的NESDTC 猜想对于Cartesian 积：Pm□Cn, Pm□Wn, Pm□Kn是成立的.

2 一些重要引理

命题1[7]设Pm(m ≥2)是m阶的路，则

引理2[8-10]设G为简单图，点u与点v是图G的两个相邻顶点，且dG(u)≥2dG(v)，则对G的任意一个2-全染色，均有w(u)/=w(v).

3 主要结果

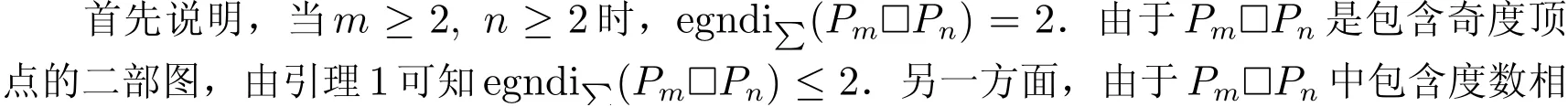
表示C3=u1u2u3u1的NESD 2-全染色f，其中52表示顶点u1的扩展和为5，且u1的颜色为2.其余符号表示的意思类似.设P, Q分别为r行s列和r行t列的模式.用Pk表示P重复出现k次的r行ks列的模式，用PQ表示P和Q依次出现的r行s+t列的模式.

情形1.1m ≡0 (mod 3).

令

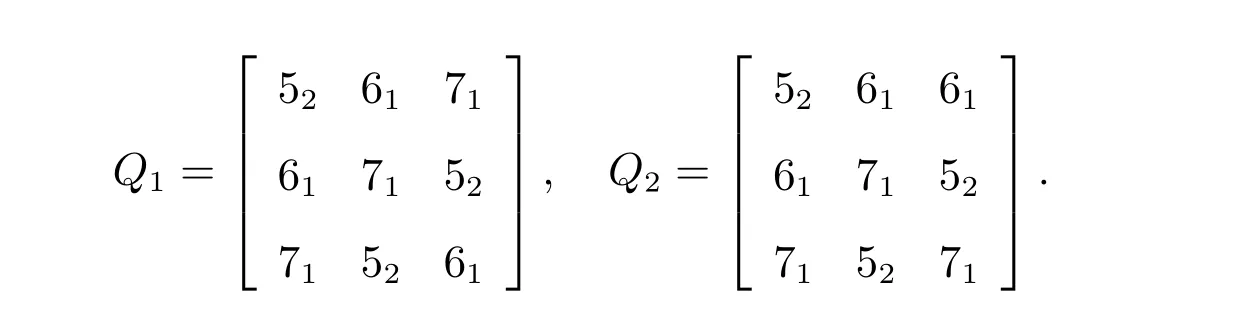
表示Cn=v1v2···vnv1的3 种不同的NESD 2-全染色.

情形2.1m ≡1 (mod 2).

用R1R2···R1对应的序列对Pm□Cn中的m个圈分别进行染色，再将这m个圈之间的边都用颜色1 染色，可得到Pm□Cn的一个NESD 2-全染色(见(R1R2R1···R2R1)′).

情形2.2m ≡0 (mod 2).

当m=2 时，用R1R2对P2□Cn中的2 个圈分别进行染色，再将这2 个圈之间的边用颜色2,1,··· ,1 依次染色，可得到P2□Cn的一个NESD 2-全染色.

用R1R2···R1R2R1R3对应的序列对Pm□Cn中的m个圈分别进行染色，再将这m个圈之间的边都用颜色1 染色，可得到Pm□Cn的2-全染色(R1R2···R1R2R1R3)′.易看出，此模式中只有第(1,m-2)个元素和第(1,m-1)个元素对应的顶点是扩展和相同的相邻顶点.由圈Cn的NESD 2-全染色g可知，第(1,m-1)个元素和第(2,m-1)个元素对应顶点之间的边颜色是1.将这条边的颜色由1 改为2，可得到Pm□Cn的一个NESD 2-全染色(见(R1R2···R1R2R1R3)′′).

综上所述，结论成立.

根据上述分析，对任意x ∈V(Pm□Wn)A，有wf′(x)=wf(x)+3.因此，对任意相邻顶点y,z ∈V(Pm□Wn)A, wf′(y)/=wf′(z).由于n ≥9，利用引理2 可知，对任意相邻顶点y ∈V(Pm□Wn)A和z ∈A, wf′(y)/=wf′(z).

因此，对任意相邻顶点y, z ∈A，有wf′(y)/=wf′(z).

综上所述，结论成立.

由文献[7]的定理8 和推论9 可以知道，Kn存在满足一定要求的邻点扩展和可区别2-全染色.该染色在如下的引理3 中给出.

引理3[7]设n ≥3, V(Kn)={v1,v2,··· ,vn}.

1) 若n是偶数，则Kn存在邻点扩展和可区别2-全染色f，使得

定理2 设m ≥2, n ≥3，则egndi∑(Pm□Kn)=2.

证明 若n=3，则Pm□K3=Pm□C3.根据定理1 可知结论成立.

情形1n是偶数且n ≥4.

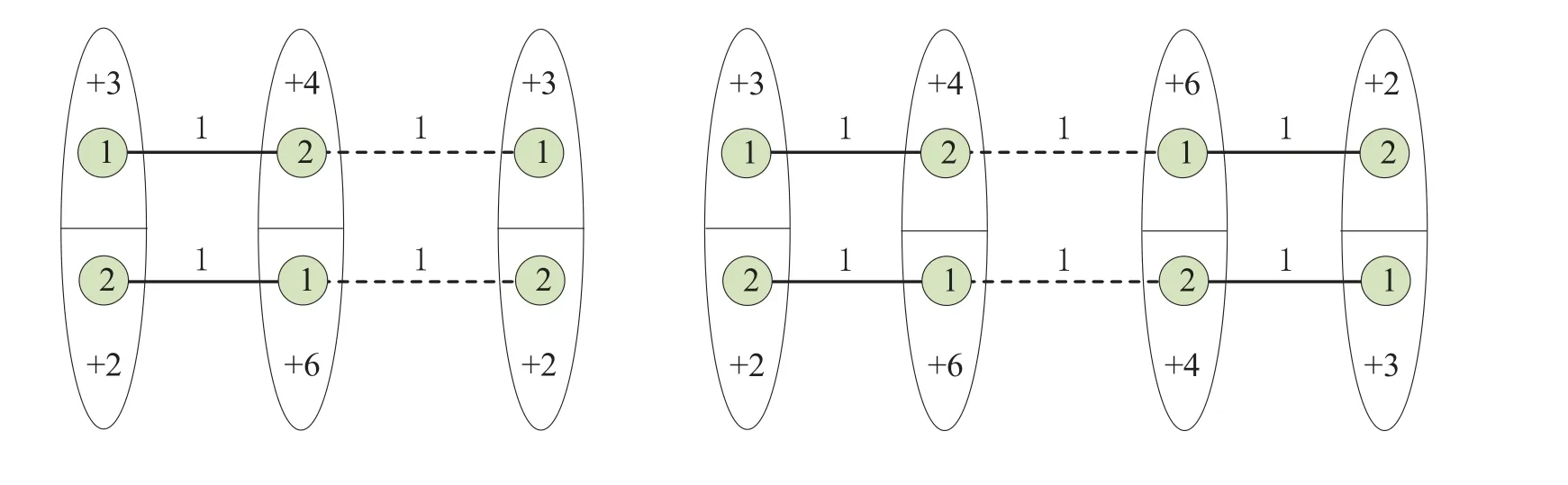
图2 n 是偶数时Pm□Kn 的NESD 2-全染色示意图

情形2n是奇数且n ≥5.

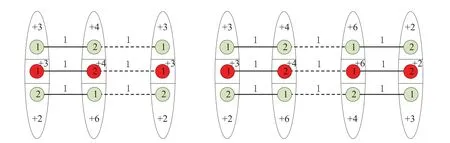
图3 n 是奇数时Pm□Kn 的NESD 2-全染色示意图