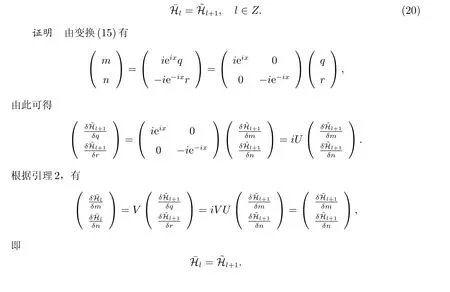对偶薛定谔方程族与导数薛定谔方程族的对应关系

2021-11-26 06:52郭明月王云波

工程数学学报 2021年5期

郭明月康婷王云波

(1. 西北大学数学学院，西安 710127; 2. 西北大学非线性科学研究中心，西安 710069)

1 引言

非线性薛定谔方程

其中γ和ρ为实参数，u(x,t)为复值函数，是光脉冲在光纤中非线性传播的基本模型，可以描述光孤子在单模光纤中的传输、超导电子在电场中的运动和等离子体中的Langnui 波等非线性波动现象.引入函数u的共轭函数v=ρ¯u，非线性薛定谔方程(1)可以表示为双哈密顿形式[1]

是相应的哈密顿守恒律.

早期，文献[2-4]中提出并系统完善了三哈密顿对偶方法.利用该方法可以由已知的双哈密顿系统构造出具有非线性色散结构，拥有非光滑孤子解的新的双哈密顿系统，称之为原孤子系统的对偶可积系统.将该方法应用到非线性薛定谔方程(1)的双哈密顿表达式上，引入一对相容的哈密顿算子

即可得到相应的对偶薛定谔系统，其双哈密顿形式为[1,2]

对偶薛定谔系统的具体形式为

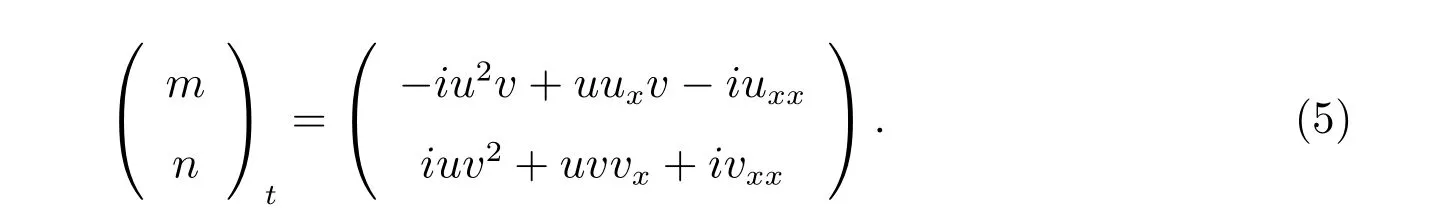
如果n= ¯m，方程组(5)约化为标量形式的对偶薛定谔方程[1,5]

非线性薛定谔方程(1)可以描述非线性脉冲在光纤中的传播，在考虑非常短的脉冲输入时，就会增加一些额外的项来解释高阶作用.此时会出现一些特殊的可积方程，包括导数薛定谔方程[5,6]

其中～u(x,t)为复值函数.如果引入函数关系

则可将方程(7)写成两分量系统形式

对于一个双哈密顿系统，由其递推算子作用在种子对称上可以生成相应可积方程族.本文主要研究对偶薛定谔方程族与导数薛定谔方程族的对应关系，通过联系两个方程族的规范变换，建立两个方程族递推算子恒等式.在此基础上，建立两个方程族中每一个可积方程以及哈密顿守恒律之间的一一对应关系.

2 对偶薛定谔方程族与导数薛定谔方程族之间的对应关系

本节考虑对偶薛定谔方程族与导数薛定谔方程族之间的对应关系.根据Magri 理论[7,8]，对于一个具有相容哈密顿算子K和J的可积双哈密顿系统，R=KJ-1为其允许的递推算子.将递推算子迭代作用在种子对称上即可生成该双哈密顿系统对应的拥有无穷多个可积方程的可积方程族，其中每一个方程都是以K和J为相容哈密顿算子的双哈密顿系统.具体地，对于对偶薛定谔方程，将递推算子¯R= ¯K¯J-1迭代作用到种子对称，即可得相应可积方程族.其正族第l个方程的双哈密顿形式为

其中对偶薛定谔方程即为该可积方程族正族的第二个方程.在负方向，负族第l个方程的双哈密顿形式为

接下来，对于非负整数l，用(dNLS)l和(dNLS)-l表示对偶薛定谔方程族正族和负族的第l个方程，用(DNLS)l和(DNLS)-l表示导数薛定谔方程族中正族和负族的第l个方程.

引理1[5]设～u(x,t)满足方程导数薛定谔方程(7)，则函数

本文在无线传感器网络与未知目标之间有相对移动的情况下研究了联合TDOA/FDOA定位方法,在文献[12]提出的半正定松弛方法的基础上提出了一种增强型的半正定松弛方法,利用增强型的优化方法有效改善了定位的精度。本文通过深度挖掘优化变量之间的内在联系,并将这些联系构造成合理的约束条件,进而将这些非凸约束松弛成凸约束对半正定规划问题进行收紧,求得了全局最优解。文章理论证明了这些约束条件是有效的,起到了收紧半正定松弛规划问题的作用。增强半正定规划问题是一个凸优化问题,它能找到近似WLS问题的全局最优解,进而避免了收敛于局部极小点的情况。