具有非局部捕食效应的藻类-贻贝系统空间分布模式研究

李 静 孙桂全

(1. 山西财经大学应用数学学院，太原 030006; 2. 中北大学理学院，太原 030051;3. 山西大学复杂系统研究所，太原 030006)

1 引言

海岸带作为连接陆地与海洋的过渡带，具有丰富的生物资源、景观资源和空间资源等，是我国人口最为稠密、社会经济最为活跃的地区譬如珠江三角洲、长江三角洲和粤港澳大湾区.海岸带生态系统作为沿海经济带最重要的生态安全屏障，在当前经济迅速发展和人为活动日益频繁等多重影响下，其生态结构和功能遭受了前所未有的威胁和挑战，因而对海岸带生态系统的研究变得更加迫切.贻贝作为海岸潮间带区域的常见种，大量的种群栖息在不同的海岸潮带地区，形成了尺度大约在1 米到100 米之间具有规律的空间分布结构，这些贻贝不仅是食物链网络的重要环节，而且也为人类供给了丰富的食物资源.因此，研究这类种群的空间分布结构对维护海岸生态系统的物种多样性起着关键作用.van de Koppel 等人[1]表明在外界环境的扰动下，生物种群在空间上的异质分布结构具有比同质分布结构更强的抵抗力和恢复力.因此，研究影响贻贝空间分布模式的因素能够为维护海岸生态系统的可持续发展提供一些建议和理论依据.

为了研究贻贝种群空间分布模式的演化规律，生物和数学方面的科研工作者已开展了相关研究内容.van de Koppel 等人[1]根据藻类的生长规律以及藻类与贻贝之间的捕食关系，首次提出了一个反应扩散对流模型来刻画瓦登海海岸上贻贝规则空间分布模式的自组织演化过程.Wang 等人[2]呈现了空间分布模式形成的详细数学分析，发现空间分布模式是非线性项作用的结果，而且具有不同波长，振幅和运动速度的多种尺度空间模式可能共存.Liu 等人[3]通过构建了一个包含贻贝、藻类和软沉积物的三变量反应扩散对流模型去分析自然界中贻贝聚集形成的空间分布模式，表明了个体行为聚集形成的小尺度网状格局和贻贝之间捕食促进与资源枯竭相互作用形成的大尺度带状空间结构提高了贻贝生态系统的复原力.Cangelosi 等人[4]利用弱非线性扩散不稳定方法研究了藻类-贻贝模型发生Turing 失稳的条件，并从数值仿真的角度展示了对应的空间分布结构.Song 等人[5]采用反应扩散方程的规范型理论研究了不考虑对流项的藻类-贻贝模型产生余维二的Turing-Hopf 分支的条件以及给出了更准确的Turing-Hopf 分支点附近动力学区域的划分，进一步证明了Turing-Hopf 的相互作用显著增强贻贝空间分布模式的多样性.Shen 和Wei[6]通过在藻类-贻贝模型中引入时滞效应，研究了在时滞参数的一些范围内模型能够产生Hopf 分支，Turing 分支和Hopf-Turing 分支.目前的这些研究工作假设贻贝捕食藻类的过程发生在同一位置的贻贝与藻类之间.事实上，某一位置贻贝生物量的增加是由其它位置的贻贝移动到此处并捕食藻类引起的，这一事实导致了贻贝与藻类的非局部捕食作用.这一过程无法直接用经典的反应扩散方程进行刻画，因此有必要寻找其他的动力学方程进行描述.而且，这种非局部的捕食作用如何影响贻贝的空间分布模式也待进一步分析求证.

本文主要通过借助非局部时滞反应扩散方程[7,8]来构建动力学模型研究贻贝与藻类之间的非局部捕食作用，并利用Turing 失稳理论研究这种非局部效应对贻贝空间分布模式的影响[9-12]，而关于这类动力学模型的Turing 失稳理论研究尚处于开始阶段.本文的内容结构安排如下：第2 节构建了具有非局部捕食效应的藻类-贻贝空间扩散模型；第3 节计算出无扩散系统存在两个常数平衡点以及分析相应平衡点的局部渐进稳定性，进一步分析扩散系统对应的特征方程根的分布情况，通过三个定理推导出系统发生Turing 失稳的条件.第4 节，通过数值模拟呈现出贻贝空间分布模式随时间的演化规律并最终形成高密度的点状空间分布结构，进一步通过参数敏感性分析方法研究了影响贻贝空间分布模式的因素；第5 节对全文进行总结和讨论.

2 模型

其中A(x,t)表示t时刻x位置的潮水边界层海藻的浓度，M(x,t)表示t时刻x位置贻贝种群的密度，其他的参数描述见表1.

表1 模型参数说明

事实上，由鞭毛运动的游动机制引起的主动横向扩散加上其在上下水层的垂直扩散组成了藻类的随机扩散，故在上述模型(1)的第一个方程中引入DA∇2A，其中DA描述藻类的扩散系数.为了更深刻地理解两种群的随机扩散对藻类和贻贝系统相互作用的影响，在这块忽略藻类的对流项，即假设V=0.考虑到贻贝能够随着潮水流动进行随机扩散并且扩散需要时间完成，t-s时刻在y位置的贻贝经过了s段时间在t时刻到达x位置并捕食此位置的藻类引起了t时刻x位置贻贝种群生物量的增加.为了建模这种非局部捕食情形，我们将在模型(1)的贻贝方程中引入时空卷积算子

进行表示，构建了如下具有非局部捕食效应的藻类-贻贝空间扩散模型

其中(x,t)∈R2×(-∞,+∞)，M(y,s)表示s时刻y位置贻贝的密度，核函数G(x,t)是可积函数，假设有如下形式

G(x-y,t-s)表示t-s时刻y位置的贻贝密度对t时刻x位置贻贝种群的影响大小，且从y位置移动到x位置所需要的时间是s.

由于上述系统(2)对应的特征方程不易求解，故直接利用Turing 失稳理论分析系统(2)是比较困难的.根据Yang 和Xu[15]的方法，通过令P(x,t) = (G*M)(x,t)，则系统(2)被转化为如下的三变量反应扩散系统

3 动力学分析

3.1 局部稳定性分析

当不考虑贻贝和藻类的扩散时，系统(4)变成如下的常微分系统

成立，则贻贝灭绝平衡点E0是稳定的.否则，贻贝灭绝平衡点E0是不稳定的.

进一步，通过求解可获得系统(5)在贻贝生存平衡点E*处的雅克比矩阵为

这里

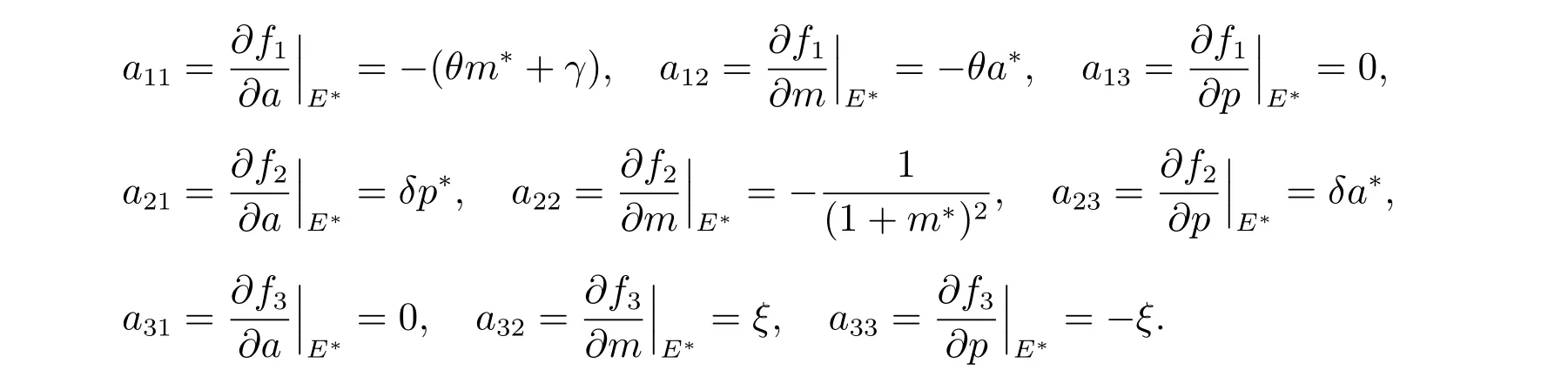
同时可推导出对应的特征方程为

若条件(H0)成立，显然有a0＞0.同时设Δ1=a2a1-a0，且记Δ1=A2θ2+A1θ+A0，其中

成立，则得到A0＞0，显然可推出Δ1＞0.根据Routh-Hurwitz 判据[16]，即当特征方程(8)对应的系数a2＞0, a0＞0 和Δ1＞0 时，其所有特征值的实部都是负的，从而表明E*是局部渐进稳定的.

图1 系统(5)的参数分岔图(γ =0.554, ξ =0.8)

3.2 Turing 失稳分析

对于海岸带上的贻贝生态系统，人们主要关注贻贝的持续生存状况以及在潮间带上的空间分布模式等信息，所以我们将研究系统(4)在贻贝生存平衡点E*处的Turing 失稳理论，给出空间分布模式存在的条件.根据3.1 部分的分析，可知E*满足方程组f1(a*,m*,p*) = 0, f2(a*,m*,p*) = 0 和f3(a*,m*,p*) = 0.对系统(4)在E*处进行泰勒级数展开并忽略高阶非线性项，可获得如下的线性系统

进一步，通过对E*=(a*,m*,p*)作非均匀时空微扰，则可令[10]

通过对特征方程(12)的系数进行分析，发现对任意的k ＞0，由于a2＞0 成立，都有b2(k)＞0，但b0(k), b1(k)和T(k)的符号大小不确定.接下来将讨论系统(4)发生Turing 失稳的条件，进而分析贻贝的空间分布模式.

定理1 如果条件(H0)和(H3)成立，同时下列条件

都成立，则存在k ＞0，使得系统(4)的贻贝生存平衡点E*变得不稳定.

证明 通过对系统(4)在贻贝生存平衡点E*处进行时空线性化，可推导出相应的特征方程(12)，且对于任意的k ＞0，都有b2(k)＞0.考虑到b0(k)的符号不确定，设置K=k2，则

其中

如果条件(C1)成立，有K2＞0＞K1.如果条件(C2)成立，可获得极小值b0(K2)＜0，并结合b0(0) =a0＞0，这表明了存在k ＞0，使得b0(k)＜0，见图2.根据Routh-Hurwitz 判据[16]，可知系统(4)的贻贝生存平衡点E*变得不稳定.

图2 三次函数b0(K)随着K 变化的示意图

定理2 如果条件(H0)和(H3)成立，同时下列条件

都成立，则存在k ＞0，使得系统(4)的贻贝生存平衡点E*变得不稳定.

证明过程与定理1 的证明过程一致，此处不再详细叙述.

定理3 如果条件(H0)和(H3)成立，同时下列条件

都成立，则存在k ＞0，使得系统(4)的贻贝生存平衡点E*变得不稳定.

证明 对于系统(4)对应的特征方程(12)，T(k)的符号大小不确定.通过设置K=k2，T可写成下面的形式

如果条件(D1)和(D2)成立，可推导出K2＞K1＞0.进一步，根据这两个极值点在T′′(K)的符号，即

如果条件(D3)成立，可获得极小值T(K2)＜0，并结合T(0)＞0，这表明了存在k ＞0，使得T(k)＜0，见图3.根据Routh-Hurwitz 判据[16]，可知系统(4)的贻贝生存平衡点E*变得不稳定.

图3 三次函数T(K)随着K 变化的示意图

英国学者Turing[9]于1952 年首次提出Turing 失稳和空间分布模式的概念，并从数学的角度去理解这个概念，即无扩散系统(常微分方程系统)的平衡点是局部渐进稳定的，而对应的这个常值平衡点在扩散系统中失去稳定性，并随时间在空间中进行自发的演化，最终形成具有规律的空间分布模式，称这一过程为Turing 失稳.

进而，根据定理1 至定理3，系统(4)发生Turing 失稳的条件被总结如下

(16)式中的3 个关系式只要有一个成立，系统(4)就会发生Turing 失稳，所以图4 给出了在不同参数值变化下，特征方程(12)的系数b0(k2)和T(k2)与波数的平方k2的关系.在前述部分已经分析出对任意的k都有b2(k)＞0 成立，故在此处无需展示b2(k2).图4(a)显示了b0(k2)＜0 的范围随着非局部捕食效应ξ或者藻类扩散率d1的增加而逐渐扩大，而b0(k2)＜0 只在贻贝对藻类消耗率θ= 1.0 时才成立，这表明了非局部捕食效应和藻类扩散率的变化更利于系统发生Turing 失稳，进而维持贻贝的空间分布模式.由图4(d)至图4(f)可以看出，对所有的k2＞0 都有T(k2)＞0 成立，说明了由于T(k)的表达式比较复杂，满足第二和三个关系式发生Turing 失稳的参数比较难寻找但理论上是存在的.

图4 特征方程(12)的系数b0(k2), T(k2)随k2 的变化情况

4 主要结果

为了直观的展示贻贝的空间分布模式，我们将利用向前差分格式对系统(4)进行数值模拟.具体步骤是先对时间进行离散化，设置时间步长Δt=0.005；再通过网格剖分的方式把二维空间区域均匀地划分成M×M个格子，其中二维空间长度和格子单元长度分别设置为Lx=Ly= 100 和Δx= Δy= 1；最后，利用向前差分格式在离散空间区域上求解系统(4).在数值模拟过程中，贻贝的空间分布结构不再随时间演化表示模拟结束.在接下来的数值模拟结果中，图片中竖条棒上的刻度代表贻贝在某个空间位置上的密度，竖条棒上颜色的深浅代表密度的增减.

4.1 空间分布模式

当参数取γ=0.554, θ=1.1, ξ=0.8, δ=1.40, d1=1.2, d2=0.04, d3=0.02 时，图5(a)至图5(d)呈现了贻贝在空间上的分布随时间演化的过程，其中图5(d)代表最终形成的空间分布模式.在初始时刻，贻贝种群均匀地分布在空间中，随着时间的推移贻贝种群在空间中聚集成条状结构，且少部分位置的密度比较高，随后贻贝种群逐渐地聚集成许多非常紧密的小群体，最终在空间上形成了高密度点状分布模式.这一过程直观的展示了自然界中贻贝在空间中的聚集过程.从图5(d)中取y= 10, y= 50 和y= 90 平行于x空间方向的3 个位置，图6 更清楚地展示出在贻贝和藻类的空间分布模式到达固定不变时，贻贝的密度和藻类的浓度在x空间方向上呈振荡的空间分布模式，进一步发现贻贝和藻类在空间上的分布呈现反相位模式，这是由贻贝与藻类之间的捕食与被捕食关系引起的.当固定x位置时，贻贝和藻类的浓度在y空间方向上也有类似的现象.

图5 贻贝的空间分布模式随时间演化的过程

图6 在y 位置固定的情形下，贻贝的密度和藻类的浓度在x 空间方向上的分布

4.2 参数敏感性分析

为了更清楚的理解贻贝的空间分布模式，需要分析系统(4)中各个参数对贻贝和藻类空间平均密度影响的大小.由于在数值模拟过程中发现参数γ, θ, δ和d3不易使贻贝种群形成空间分布模式，所以这部分不考虑这四个参数的影响.首先，粗略地分析一下非局部捕食效应ξ、藻类的扩散速率d1和贻贝的扩散速率d2对两个种群空间平均密度的影响，主要采用的方法是在其余参数固定的情形下连续改变某一参数的值导致种群的空间平均密度是否发生变化，若发生变化说明对该参数敏感，否则不敏感.其次，我们将利用Ingalls[17]提出的局部敏感性分析理论来辨识出参数敏感性的程度，这里局部敏感性系数(Slocal)被定义为

其中Par 和Res 分别表示参数和种群的空间平均密度，ΔPar 和ΔRes 分别表示参数和空间平均密度的微小改变量.若Slocal＜0 表示参数值与空间平均密度呈负相关，反之呈正相关.进一步规定[18]：若|Slocal|＜1 表征该参数是低敏感的，若1＜|Slocal|＜2 表征该参数是中等敏感的，否则是高敏感的.

从图7(a)中观察到贻贝的空间平均密度随着参数ξ的增加而变大，而相应的到达空间分布模式不变的时间缩短，这一现象表明了非局部捕食效应促进了贻贝种群的持续增长以及加速了空间分布模式的形成，有利于贻贝种群的持续生存.图7(b)展示了藻类的空间平均密度呈现了与贻贝种群相反的情形，但到达空间分布模式不变的时间与贻贝种群一致，这是因为贻贝种群在持续增长的同时需要捕食更多的藻类，进而引起藻类的空间平均密度减少.

图7 对不同ξ 值，贻贝和藻类的空间平均密度随时间变化的情况

图8(a)展示了贻贝的空间平均密度随着参数d1的增加而快速增加，然而藻类的空间平均密度却逐渐减少，同时两个种群的密度差急剧变大，产生这一现象的可能原因是藻类种群的扩散加快有助于贻贝捕食到更多的藻类，也就是促进了贻贝种群的增长但反过来抑制了藻类种群的生长，与此同时扩大了二者的密度差.图8(b)展示了贻贝的空间平均密度随着参数d2的增加先快速减少之后增加再下降，而藻类的变化趋势相对比较缓慢并展现了与贻贝相反的情形，同时二者的密度差渐渐缩小之后扩大再缩小，导致这一现象产生的原因可能是贻贝种群的扩散速率增加引起贻贝捕食藻类的能力下降，从而使得更多的藻类得到幸存，但当贻贝种群的扩散率增加到一定程度时，藻类浓度变得更多，使得贻贝捕食藻类变得比较容易，进而引起贻贝的密度增加，之后贻贝密度的增加会导致藻类浓度减少，捕食藻类变得不容易，从而贻贝的密度再次减少，相应的藻类浓度增加.

图8 贻贝和藻类的空间平均密度随d1 和d2 变化的情况

由图9(a)可知，贻贝的空间平均密度与非局部捕食效应ξ和藻类种群的扩散速率d1成正相关，与其自身的扩散速率d2成负相关，且这两扩散速率参数都为中等敏感参数，非局部捕食效应为低敏感参数.从图9(b)中可以看出藻类的空间平均密度与贻贝种群的扩散速率成正相关，而与其他两个参数成负相关，并显示对这3 个参数都是低敏感的.这一结果表明了两种群的扩散速率对贻贝的空间分布模式有显著影响，而非局部捕食效应的影响不显著，从另一个角度说明了如果人为干扰了贻贝或者藻类的运动规律可能会改变贻贝种群的空间分布模式，进而破坏海岸生态系统的稳健发展.

图9 贻贝和藻类的空间平均密度在参数改变±10%时的参数敏感性分析

5 结论

本文研究了海岸生态系统中贻贝种群空间分布模式的演化规律，基于空间中某一位置贻贝生物量的增加来源于其他位置的贻贝移动到此处并捕食藻类引起的这一自然现象，我们构建了具有非局部捕食效应的藻类-贻贝模型.为了便于分析所构建模型的Turing 失稳理论，通过考虑特殊形式的核函数并令积分项作为新变量就可把模型转化为三变量反应扩散系统(4).我们计算出无扩散系统存在贻贝灭绝平衡点和贻贝生存平衡点，并给出其局部渐进稳定的条件.进一步，根据Turing 失稳理论推导出扩散系统产生Turing 失稳的条件.然后对模型采用时空离散化和向前差分格式进行数值模拟，展示出贻贝种群的空间分布模式随时间演化的规律并发现最终形成高密度点状分布结构.对非局部捕食效应、藻类种群的扩散速率和贻贝种群的扩散速率展开了细致的敏感性分析，结果表明贻贝和藻类种群的扩散速率对贻贝种群的空间分布模式影响较大，而非局部捕食效应的影响不显著，更利于贻贝生态系统的持续演化发展.这些研究可为海岸生态系统资源的合理开发与维护提供一些理论支撑，同时也丰富了具有非局部效应的反应扩散方程的Turing 失稳理论.