基于误差原理的瞬时单位线法参数敏感性研究

周 斌

（汕尾市水利水电规划设计院，广东 汕尾，516600）

1945年C.O.Clark提出了瞬时单位线的概念，1957年J.E.Nash推导出瞬时单位线的数学方程[1]。瞬时单位线法计算设计洪水也是我国计算暴雨洪水的一种主要方法，在我国天津、河北、黑龙江等省市得到了广泛应用[2]。20世纪80年代水电部全国暴雨洪水办公室组织编制暴雨图集，诸多省份相继率定了瞬时单位线法的参数，大大推动了瞬时单位线法的广泛应用；21世纪初，全国暴雨洪水办公室又组织对暴雨图集进行修订，部分省份的瞬时单位线法参数又在更长资料系列的基础上重新率定，使计算精度进一步得到了提高[3]。

为进一步提高瞬时单位线法的计算精度，有学者研究了瞬时单位线汇流参数n、K的率定和优化[4-7]，还有部分学者提出了变雨强的瞬时单位线法[8-10]以及变时段的瞬时单位线法[11]。采用暴雨计算设计洪水时，需要先确定地理参数、产汇流参数和暴雨参数等基础参数，这些基础参数往往存在一定的误差，对暴雨洪水的成果精度产生了一定的影响；推理公式法和瞬时单位线法是常见的两种暴雨洪水计算方法，其中推理公式法的基本参数误差影响已有部分研究成果[12，13]。瞬时单位线峰值发生时间为（n-1）·K，具有急涨缓降的特性[3]。虽然瞬时单位线的相关性质已被广泛了解，但瞬时单位线与净雨过程组合后形成了暴雨洪水计算的瞬时单位法基本方程更加繁琐，使得基本参数误差分析更趋复杂。采用多元函数泰勒公式展开瞬时单位线法方程，可得到各参数的误差传播方程，初步得到瞬时单位线法各参数对地面径流过程成果的误差影响，有助于影响洪水成果精度的高敏感性参数的筛选，指引这些高敏感性参数的复核率定，以期提高洪水计算精度，促进瞬时单位线法的进一步改进和发展。

1 瞬时单位线法计算洪水的基本公式

瞬时单位线是指当输入均匀分布的单位瞬时脉冲雨量（地面净雨）时，经过n个线性串联水库的调蓄作用，在流域出口断面形成的地面径流过程。瞬时单位线的计算公式[1]为：

式中：n、K为参数；Γ为伽玛函数；t为时间。

瞬时单位线可转换为时段为△t的无因次时段单位线，任一时刻时段单位线的公式[1]为：

对于任意时刻t，瞬时单位线法出口断面的地面径流[1]为：

式中：F为流域面积；hi为第i时段的地面净雨量，hi=Hi-μi；Hi为第 i时段的暴雨量，μi为第 i时段的下渗量。

影响瞬时单位线洪水成果的要素主要有流域面积F、暴雨量H、下渗量μ以及瞬时单位线参数n、K，以下分别对此5个要素进行讨论。

2 敏感性分析

2.1 误差传递基本方程

根据（3）式，有 Q（t）=f（F，H，μ，n，K），采用多元函数的一阶泰勒公式展开，略去高阶微量，有：

式中：ξQ为地表径流量的相对误差；ξF为流域面积的相对误差；ξH为暴雨量的相对误差；ξμ为下渗量的相对误差；ξn为瞬时单位线参数n的相对误差；ξK为K瞬时单位线参数的相对误差。

（4）式中给出了统一的各基础参数相对误差传播方程，为便于讨论，以下仅讨论单一基础参数相对误差对地表径流量的相对误差的影响效果。

2.2 F的敏感性

据（4）式，若流域面积 F 存在相对误差 ξF，按（3）式计算洪水流量时将产生相应的相对计算误差ξQ，有：

2.3 H的敏感性

若任意时段暴雨量Hi存在相同的相对误差ξH，计算得到洪水流量时将产生相应的相对计算误差ξQ，有：

2.4 μ的敏感性

若任意时段暴雨量μi存在相同的相对误差ξμ，计算得到洪水流量时将产生相应的相对计算误差ξQ，有：

2.5 n的敏感性

若瞬时单位线参数n存在相同的相对误差ξμ，计算得到洪水流量时将产生相应的相对计算误差ξQ，有：

2.6 K的敏感性

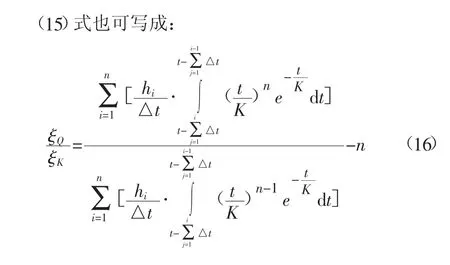
3 瞬时单位线参数n、K对洪峰发生时间的影响

4 算例

湘西南地区肖山溪以上流域，F=16.5km2，L=5.99km，J=0.0471；该流域百年一遇洪水，暴雨过程和净雨过程见表1；采用瞬时单位线计算洪水，取n0=1.246、K0=1.484[14]。

表1 各参数对肖山溪地面径流过程的敏感性分析

采用五节点分段累积的Guass—Legendre求积公式[15]求解各参数误差方程中的积分项，并忽略净雨发生前时段的影响，根据以及（3）式、（8）式、（9）式、（13）式和（16）式计算，得到各参数对地面径流过程的相对误差敏感性，见表1。另取参数n、K各缩放10%，采用（3）式计算地面径流过程及相对误差敏感性，见表2。为进一步验证参数n、K的对洪水过程的影响，采用（3）式计算参数n、K缩放幅度较大时的洪水过程，见表3。

表2 参数n、K对肖山溪地面径流过程的敏感性分析

表3 参数n、K不同取值时计算的肖山溪地面径流过程

续表3 参数n、K不同取值时计算的肖山溪地面径流过程

从表1可见，暴雨的相对误差传播敏感性最高，下渗量的影响则相对较小；从表2可见，随着参数n、K的加大，会使得起涨段更为平瘦，峰值减小，洪水回落期更偏丰满；对比表1和表2可见，根据地面径流过程计算的参数n、K敏感性与（13）式和（16）式计算成果出入不大。另外，从表2和表3可见，随着参数n、K的加大，虽然洪峰发生时间略有后移的趋势，但这种趋势不显著。

5 结语

计算暴雨洪水的瞬时单位线法在我国应用较广，该方法的地理参数、产汇流参数和暴雨参数等原始参数往往存在一定的误差，受其影响地面径流成果也存在相应的误差。利用多元泰勒公式可推导出各主要参数相对误差产生的地面径流过程误差影响公式，结合典型计算实例表明：暴雨的相对误差传播敏感性较高，具有一定的放大作用；流域面积的相对误差会导致地面径流过程等量的相对误差；下渗量的相对误差传播敏感性总体相对较小，局部仍有可能较大；参数n、K的加大，会使得地面径流峰值减小，上涨段更为平瘦、回落段更为丰满，并存在不显著的峰值发生时间后移趋势。