基于改进SEIR算法的疫情传播趋势检测方法
燕 杨, 郭皓钰, 魏宇航, 尤紫如, 肖志强, 黄文博
(1. 长春师范大学 计算机科学与技术学院, 长春 130032; 2. 吉林大学 白求恩第一临床医学院, 长春 130021; 3. 吉林大学 地球科学学院, 长春 130021)
目前, 新型冠状病毒(2019 coronavirus disease, COVID-19)正在世界范围内广泛传播. 因此, 准确检测COVID-19确诊病例及疑似病例的传播趋势, 制定切实可行的防控措施, 以减少COVID-19突然爆发导致的人员伤亡和经济损失至关重要[1]. 目前, 通过动力学算法对COVID-19疫情传播趋势进行研究和分析已有许多成果. 例如: 崔景安等[2]把新发传染病动力学算法应用于COVID-19检测, 并利用该算法与再生矩阵相结合, 计算得到了控制措施实施过程中的有效再生数或控制再生数; 王志心等[3]根据SEIR传播理论, 通过机器学习法预测了疫情拐点及确诊人数; Shen等[4]在现有流行病学资料和动力学算法的基础上, 检测了疫情的高峰时间和规模及指定日期感染人数; 魏永越等[5]通过构建SEIR(susceptible-exposed-infectious-removed)+CAQ(SEIR with infected components, asymptomatic infected, and quarantined)算法, 预测了疫情的终止时间及在防控措施不变前提下全国累计确诊病例数目; 康观龙等[6]也利用该算法对COVID-19形式进行了检测, 但由于未考虑到潜伏期也具有感染性, 所以仿真实验结果与实际公布数据有差距. 研究表明, COVID-19的潜伏期患者具有较强的传播能力, 而疫情传播动力学算法忽略了潜伏期患者导致的传播风险; 且当前检测方法中均未考虑防控措施与集中收治等因素对疫情的遏制作用. 因此, 本文针对COVID-19疫情的传播特点, 首先分析传统SEIR算法的优缺点, 然后对算法进行改进, 使其更适用于COVID-19疫情传播趋势的分析和检测. 实验结果表明, 本文算法比目前已有的其他算法更有效.
1 传统SEIR算法

图1 SEIR算法的四类人群感染阶段Fig.1 Four types of population infection stages of SEIR algorithm
传统SEIR算法将检测人群分为四类, 易感人群S(Susceptible)、潜伏人群E(Exposed)、感染人群I(Infective)和移除人群R(Removed). 易感人群指未感染但缺乏免疫能力, 与感染者接触后易受到感染的群体; 潜伏人群指处在潜伏期的感染者, 不具备传染能力; 感染人群指已感染的人; 移除人群指因病愈或死亡而不再参与感染和被感染过程的人. SEIR算法的四类人群感染阶段如图1所示. 其中: 接触率β表示易感人群(S)和潜伏人群(E)之间传播疾病的概率; 转换率δ表示潜伏个体具有传染性的比率, 若平均潜伏期为Y, 则δ=1/Y; 康复率γ表示感染后平均免疫时间的倒数, 即γ=1/D, 其中D为平均免疫时间; 在康复阶段后, 感染人群进入移除阶段(恢复或死亡). SEIR算法的微分表达式为


设S(t),E(t),I(t),R(t)分别表示随时间变化易感染人群、潜伏期人群、确诊人群以及移除人群的变化, 设单位时间为t, 则每隔一段时间后, 易感染人群、潜伏期人群、确诊人群以及移除人群的数量为
由一阶导数的定义可知, 在单位时间t内x的变化为
当Δt→0+时, 可由式(5)~(8)推出式(1)~(4). 传统SEIR算法成立的前提是假设一个封闭的种群, 人口总数固定, 没有出生, 没有死亡, 也没有新个体的引入, 人口混合居住在一起, 处于潜伏状态的个人已经被感染, 但不具有传染性. 而事实表明, COVID-19病原菌的潜伏时间与感染时间呈均匀分布, 潜伏期越长, 传染性越强. 即传统SEIR算法认为正处在潜伏期的人没有传染能力, 但COVID-19在潜伏期也具有一定的感染性. 并且算法建立在无外界干预的情形下, 不能处理管控带来的变化. 因此, 本文针对该问题进行改进.
2 改进SEIR算法
在人均传染率一定的情形下, COVID-19病例接触率在公众不了解和病毒变异的早期增加, 在严格的防控政策下减少. 而传统SEIR算法是建立在外力无干预的情形下, 因此, 本文对传统SEIR算法中的接触率β添加一个衰减函数, 通过对数据的拟合, 得到随时间增长而改变的β, 使算法能更好地适应管控防疫措施带来的变化. 假设接触率β遵循Weibull函数的斜率函数, 通过该函数可得到接触率β每天的估计值, 该估计值将用于SEIR的动态算法. Weibull函数定义为
β(t)=exp{-(t/L)kln2},
(9)
其中:L为衰减速率, 可以是衰减到1/2的时间, 也可以是完全衰减的时间;k为形态参数(无维数);t为时间;β(t)为接触率随时间变化的函数.
由于COVID-19中处于潜伏期的人仍然有感染他人的能力, 因此, 计算易感人群随时间的变化ds/dt时接触率将不是β(S×I)/N, 而是β(S+δ×E)×I)/N.将处于潜伏期的人也计算在内, 所以潜伏人群随时间的变化dE/dt应改为β(S+δ×E)×I)/N-δ×E.因此
其中δ为转换率,β为接触率,I为感染人群,E为潜伏人群,S为易感人群,t是时间,N为总人口数. 引入CFR(case fatality rate)作为死亡率, 移除人数中包含死亡人数DF为
DF=γ×I×CFR,
(12)
其中γ为康复率,I为感染人群, CFR为死亡率.
在Weibull函数β(t)、死亡率CFR、形态参数k和衰减速率L确定的情形下, 通过解SEIR的微分方程, 可得到易感人群S、潜伏人群E、感染人群I和移除人群R关于时间t的函数. 从而做出对确诊人数的趋势估计, 与实际确诊人数进行对比, 计算其均方差MSE作为损失函数, 优化损失函数即可得到最佳参数, 使用这些最佳参数对疫情传播趋势进行检测.
3 仿真实验
下面对改进的SEIR算法进行仿真实验, 并与ARIMA算法及原始SEIR算法的检测结果进行对比. 仿真实验平台为Python3.6, tensorflow2框架及Jupyter notebook. 给定的初始条件为转换率δ=0.2, 康复率γ=0.37, 接触率β=2.5. 本文实验数据来自COVID-19开放研究数据集(CORD-19)[7].
3.1 评价标准
为能有效与其他算法检测结果进行比较, 本文采用均方误差(mean square error, MSE)作为最终评价标准, 均方误差是反映估计量与被估计量之间差异程度的指标. 设时间t是根据子样本确定总体参数θ的一个估计量, (θ-t)2的数学期望称为估计量t的均方误差, 即δ2+b2, 其中δ2与b分别是t的方差与偏置.
3.2 仿真实验数据预处理
当环境中全为易感染人群时, 平均每名患者在其患病期可传染的人数为基本再生数, 记为R0. 在t时间段内平均每个患者在其患病期间感染的人数称为有效再生数, 记为Rt. 基本再生数是判断疫情爆发状态的关键指标, 当R0>1时, 每个患者在其患病期至少感染一个人, 此时疫情将大面积扩散; 当R0<1时疫情将会逐步减轻. 有效再生数在判断疫情传播时具有相同作用. 经过多次交叉测试, 最终将基本再生数R0=2.2, 死亡率CFR=0.02, 形态参数k=2, 衰减速率L=50, 作为初始值代入算法进行检测.
3.3 仿真实验结果与分析
为验证算法的拟合及检测效果, 本文将数据分为训练集和测试集两部分. 利用训练集的数据训练算法, 测试集的数据验证算法的准确程度并判断算法的检测效果. 图2为本文算法的检测结果. 由图2可见, 以数据集中的纽约数据为例, 经过9 000次训练后, 本文算法检测结果与预期基本符合.
下面将本文算法与传统SEIR算法、ARIMA算法及文献[8]算法进行比较, 结果如图3~图6所示. 由图3~图6可见, ARIMA算法与传统SEIR算法均无法检测到疫情拐点, 并且ARIMA时间序列算法由于误差的迭代, 随着时间的增加, 偏差也逐渐增大, 最终呈现出指数增长, 而文献[8]算法修改β函数时未能从根本上表达COVID-19的特点. 本文算法对数据集中各地趋势检测的准确率均明显高于其他算法, 针对该数据集特点采用Weibull函数的结果比Hill衰减函数的效率更高, 且在长期检测方面, 由于本文算法引入了衰减函数, 使得传染率β能随时间变化, 符合在防控措施下的疫情发展需求.

图3 改进SEIR算法检测结果Fig.3 Detection results of improved SEIR algorithm
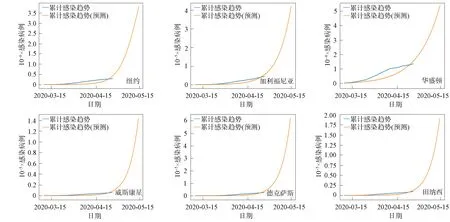
图4 传统SEIR算法检测结果Fig.4 Detection results of traditional SEIR algorithm

图5 ARIMA算法检测结果Fig.5 Detection results of ARIMA algorithm

图6 文献[8]算法检测结果Fig.6 Detection results of literature [8] algorithm
本文算法与其他算法仿真实验结果的均方误差MSE对比结果列于表1. 由表1可知, 平均MSE分别为: 本文算法0.11; 原始SEIR算法1.93; ARIMA算法0.33; 文献[8]算法0.40. 表明本文算法性能最好.

表1 本文算法与其他算法的MSE对比
综上所述, 本文通过改进SEIR算法对COVID-19病毒的传播与发展情形进行了检测, 并与其他3种算法进行了对比仿真实验. 实验结果表明, 本文改进SEIR算法衰减函数的形态参数k值调整为1时, 检测趋于稳定, 相比其他算法均方误差MSE值显著降低, 对COVID-19病毒的传播与发展检测准确率更高, 可为制订未来疫情防控决策提供理论支持与借鉴.

