面向自适应计算的局部四面体网格重划分*
刘田田, 郑 澎, 冷珏琳, 刘伟杰, 徐 权, 杨 洋
(1. 中物院高性能数值模拟软件中心, 北京 100088; 2. 北京应用物理与计算数学研究所, 北京 100094; 3. 中国工程物理研究院 计算机应用研究所, 四川 绵阳 621900)
自适应有限元方法是求解偏微分方程常用的数值方法[1-3], 网格分布是影响有限元计算结果精度的重要因素. 网格自适应技术[4]近年来得到广泛关注[5-7]. 网格自适应技术将所求问题的物理特性、数值计算方法和网格分布有机地结合, 在求解过程中不断根据数值解的性质对网格分布进行调整. 目前, 网格自适应技术主要实现途径有3种:p自适应[8]、r自适应[9]和h自适应[10].p自适应方法根据物理场特性选取高精度数值求解方法;r自适应保持网格节点总数不变, 通过移动网格点的坐标改善网格的分布;h自适应通过对网格进行粗化或细化改变网格的分布,h自适应由于其独有的灵活性, 已成为目前应用最广泛的网格自适应方法.
h自适应方法分为两类: 网格局部变换法[11]和网格重划分法[12]. 局部变换法基于模板直接分解或合并现有的网格, 目前常用的模板包括正则模板[10,13]和二分模板[14-16]. 基于模板分解或合并时, 为保证网格的协调性, 需要处理调整区域和非调整区域的过渡, 如果处理不当, 则会导致调整网格影响区过大. 局部变换法思想简单, 易于实现, 但只能生成各向同性网格, 且网格放粗需要复杂的数据结构管理. 网格重划分方法[17]对局部的网格进行重构, 易保证网格的协调性, 可以灵活控制网格尺寸的分布, 且尺寸过渡平滑, 粗化和细化可同时完成, 但效率低于局部变换法, 且不易实现. 自适应网格重划分方法在二维情形下已经发展的较成熟, 但在三维情形下仍是一个较大的挑战[18]. 自适应网格重划分方法包括两类: 一类是通过局部拓扑变换实现网格重划分[18-19], 另一类是利用网格生成方法进行全局网格重划分[20-23].
当模拟的对象是复杂多部件计算机辅助设计(CAD)模型时, 除自动生成捕捉几何特征的初始网格较困难[24-25]外, 生成满足计算要求的自适应网格也较难. 与单部件模型相比, 多部件CAD模型通常具有几何特征复杂、部件间存在表面接触等特点, 这些特点对生成保形的、协调的自适应网格都很关键. 由于多部件CAD模型的特征复杂, 因此采用基于拓扑变换的网格重划分方法很难保证模型的几何特征和网格质量. 此外, 由于多部件模型生成的网格规模一般较大, 采用全局网格重划分的方法进行自适应网格生成非常耗时. 因此, 为在保证网格质量的同时减少计算量, 本文采用局部网格重划分的方法. 局部网格重划分技术是有限元分析的重要内容, 可极大减少网格重划分的时间, 已广泛应用于CAD模型的设计修改过程[26-28], 但在自适应计算的网格生成中应用较少.
本文面向多部件CAD模型, 提出一种适用于自适应计算的局部四面体网格重划分算法, 利用前沿推进法和Delaunay方法对待调整区域进行网格重划分. 该算法是基于中物院高性能数值模拟软件中心和中国工程物理研究院计算机应用研究所联合研发的前处理引擎SuperMesh[29]实现的, 目前该算法已集成到SuperMesh中.
1 局部四面体网格重划分算法
自适应计算方法的整体流程如图1所示. 输入CAD模型, 生成初始网格并进行初场计算后, 由分析人员循环进行误差分析, 以确定网格调整信息、计算自适应网格生成和数值计算等过程, 直到满足收敛精度. 误差分析时误差评估准则的选取是数值模拟阶段的重要内容, 在实际计算时, 由分析人员制定误差评估准则并确定网格调整信息, 误差大的区域网格更细密, 误差小的区域网格更粗化. 图 1中计算自适应网格生成的流程如图2所示, 输入是CAD模型、上一次计算的网格及网格调整信息, 输出是用于下一次计算的新网格. 由于计算误差决定了网格调整信息, 因此, 重生成网格满足物理自适应的要求. 在网格重生成过程中考虑了几何特征, 可同时满足几何自适应的要求. 本文不讨论计算误差评估准则, 只讨论确定网格调整信息后, 自适应网格的生成方法.

图1 自适应计算流程Fig.1 Flow chart of adaptive computation
计算自适应网格生成算法流程包括以下三部分.
1) 构建影响区: 为使网格平滑过渡, 将输入的待调整网格向外扩张指定单元层, 得到新的待调整网格区域.
2) 待调整区域内网格重划分: 在所有待调整的网格单元中, 根据规则提取连通子域, 并在子域内采用由线到面、由面到体的顺序重新生成网格.
3) 合并网格: 将待调整区域内的新网格与固定区域内的网格合并, 得到下一次计算的网格.
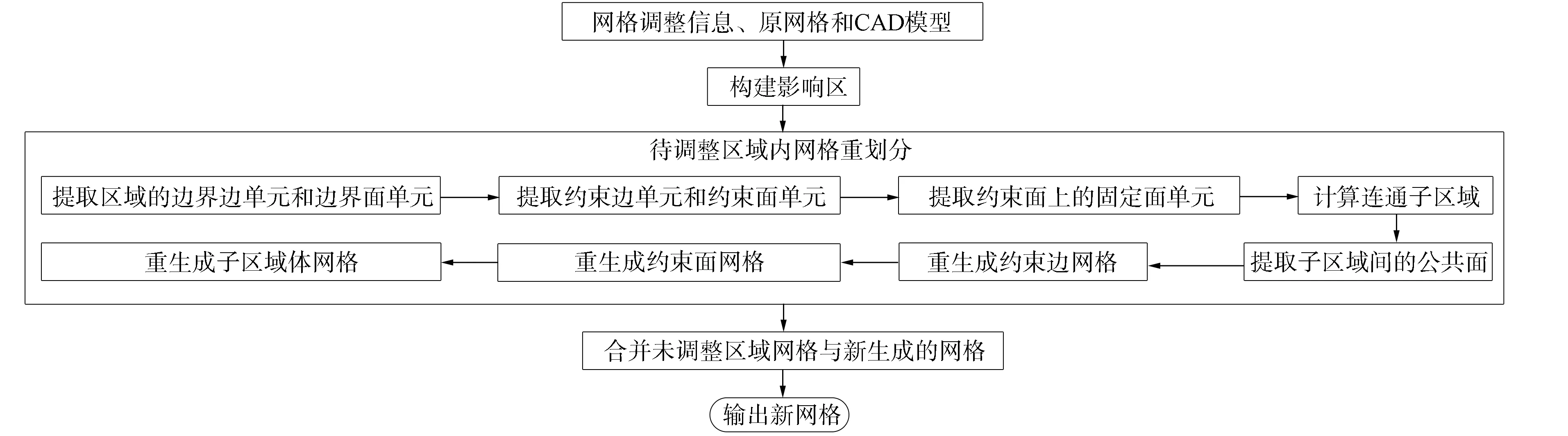
图2 计算自适应网格生成算法流程Fig.2 Flow chart of computing adaptive mesh generation algorithm
1.1 构建影响区
为保证待调整区域和固定区域之间的网格尺寸平滑过渡, 减少计算误差, 引入待调整单元影响区的概念. 影响区内的单元是从待调整区域到固定区域的过渡单元. 将计算结果给出的待调整网格单元列表记为T={ti,i=1,2,…,n},ti对应的原尺寸和目标尺寸分别为si和oi. 对每个单元ti∈T构建影响区, 构建影响区不仅要找出被影响的单元, 还要计算每个被影响单元的目标尺寸.
影响区的构建方法是以每个待调整单元为中心向外扩指定单元层l, 即
R={ri|ri∉T, ∃tj∈Ts.t.dist(ri,tj)≤l},
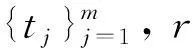
图3为不同范围影响区产生的网格, 其中红色圈内的单元是待加密单元. 由图3(B)~(D)可见, 影响区范围越大, 网格尺寸过渡越平滑. 下面涉及的网格待调整区域包含计算结果提供的调整区和算法构建的影响区两部分.

图3 不同影响区范围产生的网格Fig.3 Meshes generated by different influent regions
1.2 待调整区域网格重划分
网格重划分需要考虑3个关键问题: 1) 如何保证网格的协调性; 2) 如何保证网格满足几何保形; 3) 如何满足计算的网格尺寸要求. 网格的协调性需要考虑两部分: 1) 待调整区域和固定区域之间网格单元的协调性; 2) 待调整区域内CAD模型中不同部件之间网格单元的协调性. 为保证待调整区域和固定区域之间的网格协调性, 在重划分网格时, 要保持两个区域之间的面网格固定不变, 将该面网格作为网格重划分的约束. 为保证CAD模型中部件间网格的协调性, 采用线→面→体的顺序生成网格, 以保证不同部件之间的公共点、公共边和公共面网格完全协调. 为使网格满足几何保形, 在采用线→面→体的顺序进行网格重划分时, 把位于CAD边和CAD面附近的网格点向CAD模型进行投影. 为满足计算的网格尺寸要求, 根据网格调整信息构建平滑的局部尺寸函数指导网格生成.
待调整区域内可能包含多个连通子区域, 每个连通子区域可能横跨了CAD模型的不同部件, 为保证网格的协调性和几何保形性, 本文提出了如图2所示的网格重划分算法. 算法的输入包括CAD模型、网格S、待调整区域单元列表T、每个单元的目标尺寸列表O. 输出是重划分后的网格.
1.2.1 提取边界边和边界面
图4为网格重划分算法示意图. 首先构建网格单元的邻接关系, 提取待调整区域的所有外表面单元, 筛选不在CAD模型上的单元, 记为边界面, 如图4(B)中的蓝色单元. 边界面的外边界记为边界边. 边界边和边界面网格固定不变, 不参与网格重划分, 以保证待调整区域与固定区域之间网格的协调性.

图4 网格重划分算法示意图Fig.4 Schematic diagram of mesh remeshing algorithm
1.2.2 提取约束边、约束面和固定面
为保证几何保形, 提取待调整区域内属于CAD模型边界上的所有边单元和面单元. 对于调整区域内所有属于CAD模型上的边单元, 如果不属于边界边, 则记为约束边; 如果属于边界边, 则记为固定边. 所有不包含固定边的且属于CAD模型边界上的面单元, 记为约束面, 如图4(B)中的绿色单元; 包含固定边的面单元, 记为固定面, 如图4(B)中的红色单元. 为保证网格的协调性, 固定面不参与网格重划分.
1.2.3 计算连通子区域
为保证CAD模型不同部件之间网格的协调性, 根据约束面和四面体单元所属的部件, 将待调整网格区域分为若干个连通子区域. 一个连通子区域中的所有单元都属于同一个部件且区域内部不包含约束面, 所有约束面都在连通子区域的边界上. 算法描述如下.
算法1提取连通子区域算法.
输入: 待调整网格单元列表T, 约束面列表C;
输出: 连通子区域列表List;
步骤1) 初始化连通子区域列表List为空;
步骤2) 初始化连通子区域L、队列P, 将T的第一个单元作为种子单元, 加入P中;
步骤3) 如果P非空, 则取出P中的第一个单元τ, 加入L中; 遍历τ的所有邻接单元, 如果邻接单元还未被分组, 与τ属于同一个几何实体并且公共面不是约束面, 则将邻接单元插入P中; 如果P非空, 则重复执行步骤3); 如果P为空, 则执行步骤4);
步骤4) 将L加入到List中, 若T中所有单元都已经被分组, 则结束算法; 若存在单元未被分组, 则执行步骤5);
步骤5) 初始化L, 选取T中未被分组的一个单元加入P中, 执行步骤3).
通过算法1提取出图4(C)中的两个连通子区域. 由于连通子区域是根据所属的CAD部件区分的, 因此连通子区域之间的公共面都是约束面.
1.2.4 约束边网格重划分

1.2.5 约束面网格重划分
设约束面单元f的相邻四面体分别为ti和tj, 则f的目标尺寸为
of=0.5Lmin·(oti/sti+otj/stj),
其中Lmin是f的最短边长.
约束面网格重划分利用前沿推进方法. 为保证重划分后的面网格是几何保形的, 将重划分的网格点投影到其对应的几何面上. 根据约束面单元所属的几何面, 提取约束面网格的连通子区域. 约束面网格连通子区域的查找方式与待调整区域连通子区域的计算方式类似. 图4(E)中不同颜色表示不同的约束面连通子区域, 每个约束面连通子区域内, 采用前沿推进方法对网格进行重划分. 算法描述如下.
算法2约束面网格重划分算法.
输入: 约束面连通子区域F, 约束面单元的目标尺寸O;
输出:F内的新网格;
步骤1) 调整S中单元的绕向, 使所有单元绕向协调;
步骤2) 根据每个约束面单元的目标尺寸, 构建S内的局部尺寸函数f;
步骤3) 提取S边界上的边单元, 获取重划分后的约束边单元, 构造区域的新边界E;
步骤4) 根据新边界E和尺寸函数f, 利用前沿推进方法重新生成S内的面网格, 将新网格点投影到CAD面上.
对比图4(B)和图4(E)中的球体表面可见, 加密后的球面比加密前更光滑, 更贴近真实几何形态.
1.2.6 连通子区域内体网格重划分
根据连通子区域内每个四面体单元的目标尺寸, 构建子区域内的局部尺寸函数. 提取每个子区域边界上的面单元, 包括边界面、固定面和新生成的约束面网格. 以边界面单元为约束, 尺寸函数作指导, 利用Delaunay算法生成所有子区域内的四面体网格.
1.3 合并网格
将调整区域内重划分的网格和固定区域内的网格合并, 删除冗余点, 在网格单元上设置对应的CAD几何信息, 得到新的网格.
2 实验结果分析
2.1 带孔板拉伸问题结构应力分析
基于本文的自适应网格生成技术, 对经典的带孔板拉伸问题[27]进行应力分析. 微分方程


带孔板拉伸结构应力分析的物理模型如图5(A)所示. 由图5(A)可见, 该模型包含两个部件, 左右两侧受均匀拉力, 材料为弹性. 根据问题的对称性, 模拟计算其1/4. 该结构在孔的角点处易产生应力集中, 自适应网格能很好地反应应力集中现象. 该实例的应力相对误差范数从初始的7.6%下降到1.4%, 初始网格和自适应网格分别如图5(B)和图5(C)所示. 图5(D)是利用中物院高性能数值模拟软件中心基于JAUMIN[28]研发的力学软件JSolid计算得到的应力分布图.

图5 带孔板拉伸结构应力分析Fig.5 Stress analysis of tensile structure with orifice plate
2.2 舰船模型网格加密
下面对舰船模型进行测试, 图6为舰船模型一次自适应加密前后的对比结果. 由图6(D)可见, 重划分后的网格更贴近真实的几何形态, 且尺寸过渡平滑.

图6 舰船模型网格调整前后对比Fig.6 Comparison of ship model mesh before and after adjustment
网格质量指标采用体积-边长比衡量, 体积边长比的计算公式为
其中V表示四面体单元的体积,li表示四面体的边长. 体积边长比的范围是[0,1], 当q=1时为正四面体. 图7为网格调整前后四面体网格体积边长比的统计对比结果. 由图7可见, 重划分后的网格质量有明显提升. 由于初始网格较稀疏, 所以在某些特征附近网格质量较差. 网格重划分后, 提高了这些几何特征附近的网格质量.
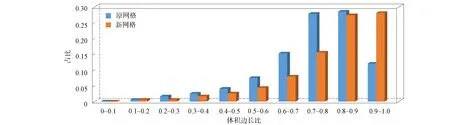
图7 网格调整前后的质量对比Fig.7 Comparison of quality before and after mesh adjustment
综上所述, 本文提出了一种面向自适应计算的局部四面体网格重划分算法. 该算法根据计算结果给定的自适应源进行网格重划分, 得到的网格满足协调性、几何保形性, 且尺寸平滑过渡. 该算法适用于包含多实体的复杂CAD模型, 可在一定程度上保证网格的质量.

