属性异构信息网络的半监督协同聚类
刘嘎琼, 韩 斌, 王东升, 严 熙, 李会格
(江苏科技大学 计算机学院, 江苏 镇江 212100)
异构信息网络(heterogeneous information networks, HINs)由多个节点及其之间的关系组成, 用于对复杂数据集进行建模[1]. 与传统的节点和边都属于单一类型的同构网络相比, HINs能有效地融合更多的结构信息, 具有更丰富的语义[2]. 因此, 如何建立高效的HINs对于数据挖掘至关重要[3].
目前, 元路径被广泛用于提取HINs节点间异构连接的结构语义. 熊菊霞等[4]提出了获取不同类型节点语义的元路径, 并提出了评价HINs中相同类型节点相似度的路径模型. 考虑到不同元路径的影响, 张文凯等[5]提出了将多条元路径的相似性度量相结合. 但这些方法都是主要利用HINs的结构信息, 忽略了节点的属性, 因此导致隐藏信息未得到充分挖掘. 为描述HINs中的顺序属性和分类属性, 一种有效的方法是将节点的属性视为向量, 其中每个维度表示一个属性. 史加荣等[6]通过将不同元路径的节点相似性与权重相结合, 设计了一种无监督的负矩阵分解算法; 朱超平等[7]通过分别构造链接图和属性图整合结构信息和属性信息. 但目前的研究主要集中在对同一类型节点的相似性搜索上, 而未对HINs中不同类型节点的聚类进行联合分析. 实际上, 由于不同类型节点之间潜在的相关性(相似性), 不同类型的聚类通常是相互关联的.
与传统聚类方法不同, 协同聚类利用特征和样本之间的对偶性, 实现特征和样本的同时聚类. 此外, 协同聚类方法能在不同节点类型的聚类之间获得潜在的对应关系, 从而使得到的聚类更具可解释性. 董立岩等[8]将文档视为一个二部谱图, 然后根据图寻找最小割点划分对文档和单词进行联合聚类; 夏菁等[9]提出了同时对基于元路径的相似度矩阵进行因子分解, 实现了不同类型节点的联合聚类; 周慧等[10]提出通过测量纹理视图和颜色视图等视图中节点的相关性对多视图数据进行联合聚类. 但这些模型在处理属性HINs时, 由于存在基于结构和属性的多个相关度量, 无法对HINs进行聚类.
为解决上述问题, 本文提出一种基于属性异构信息网络的半监督协同聚类框架(SCCAIN). 该方法利用多条元路径和可学习的权值对结构进行度量关联性和不同空间属性的参数化属性关联度量. 在3个数据集上的实验验证了本文方法的有效性.
1 预备知识
定义1异构信息网络(HINs)表示为G={V,ε,T,R}, 其中V是节点集,ε是链接集,T是节点类型集,R是关系或链接类型集. 在HINs上有两个映射函数, 一个是节点类型映射φ:V→T, 以获取节点类型, 另一个是链接类型映射ψ:ε→R, 以获取链接类型. 其中|T|+|R|>2.
定义2属性HINs是一种特殊类型的HINs, 其形式为G={V,ε,F}. 与传统的HINs相比, 属性HINs具有丰富的属性信息, 即F={fv}, 其中fv是节点v的属性向量.
异构节点的属性向量可能具有不同大小和含义. 以图1为例, 有3种类型的节点, 即T={A,P,C}, 2种类型的链接. 此外, 作者和会议都包含向量形式的几个属性. 由于作者和会议的属性表示不同的含义, 因此分别使用平行四边形和正方形区分.
设A,P,C分别表示作者、论文和会议, 作者的属性是他们感兴趣的研究领域, 包括网络嵌入、异常检测、非负矩阵分解(NMF)和共聚类, 而会议的属性是诸如聚类、主题建模和推荐系统等主题.

图1 属性化异构信息网络示例Fig.1 Example of attributive heterogeneous information networks
如图1所示, 元路径A-P-C的源节点和目标节点是作者和会议. 此外, 不同的元路径将捕获不同的语义, 有助于聚类. 例如,A4和C3可以通过A-P-C或A-P-A-P-C连接, 第一个元路径表示发布, 而第二个元路径是通过共同作者捕获作者和会议的相关性.
属性HINs的半监督协同聚类问题: 给定一个属性HIN, 其形式为G={V,ε,F}, 一些连接源节点Vs和目标节点Vt的元路径, 以及一些节点之间的必须链接Mss,Mst,Mtt和不能链接Css,Cst,Ctt约束, 目标是同时考虑结构及属性信息, 并生成具有整体相关性矩阵X的Vs和Vt的聚类. 特别地,Vs和Vt分别表示X的行实例和列实例. 此外,M/C的下标表示约束的类型. 例如,Mst是Vs和Vt之间必须连接的约束.
2 方法设计
2.1 总体框架
图2为SCCAIN的总体框架. 在该框架中, 首先, 分别设计基于元路径Λ重要性的结构相关性度量和基于潜在参数A的属性相关性度量, 考虑到这两种相关性, 本文将它们组合成一个整体相关性度量; 其次, 设计一个基于非负矩阵三因子分解(ONMTF)的半监督协同聚类模型, 该模型将相关性矩阵分解为S和T这两个聚类分布, 以及一个辅助矩阵W. 此外, 由于相关性度量和协同聚类的性能相互影响, 因此将这两部分整合到一个联合的框架中, 并对其进行优化, 从而得到最终的异构节点聚类结果.

图2 SCCAIN的总体框架Fig.2 Overall framework of SCCAIN
2.2 属性HINs的相关性度量
2.2.1 结构相关性
采用异构网络中相关性度量的通用框架(HeteSim)度量第i个s型节点与第j个t型节点之间的相关性, 表示为
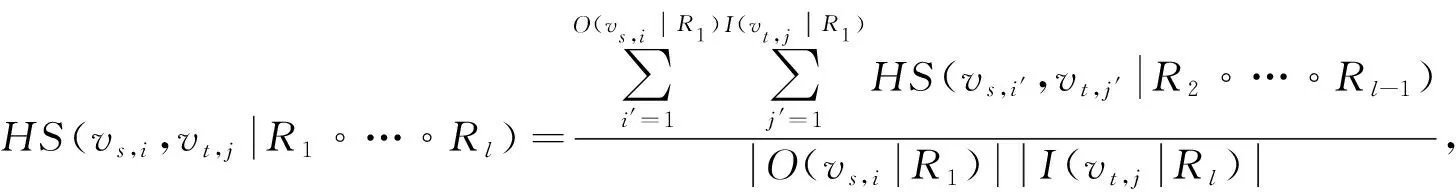
(1)
其中vs,i和vt,j分别表示第i个源节点和第j个目标节点,HS(vs,i,vt,j|R1∘…∘Rl)为元路径R1∘R2∘…∘Rl上vs,i和vt,j之间的HeteSim值,O(vs,i|R1)为基于关系R1的vs,i的外邻域,I(vt,j|Rl)为基于关系Rl的vt,j的内邻域. 如果vs,i′=vt,j′, 则HS(vs,i′,vt,j′|R(l+1)/2)=1, 否则为0. 与传统的只计算同构节点相似度基于元路径的相似度算法(PathSim)或相关性不对称的路径约束随机游走模型(PCRW)不同, HeteSim可以度量不同类型节点的相关性.
考虑到存在多个元路径, 每个元路径表示一种形式的结构相关性, 如图2所示, 这里将元路径重要性权重λP分配给具体的相关性HS(vs,i,vt,j|P), 然后计算结构相关性, 即

(2)

2.2.2 属性相关性
给定第i个源节点的特征fs,i和第j个目标节点的特征ft,j, 不可能直接度量fs,i和ft,j的相关性. 通过将不同空间中的属性映射到同一空间中, 进一步计算vs,i和vt,j的属性相关性度量:

(3)
其中XA是属性相关性矩阵,A∈RDs×Dt是不同空间的属性向量的相关参数,σ(·)是激活函数, 采用ReLU函数保持属性相关性为正.
2.2.3 整体相关性
SCCAIN综合考虑了结构信息和属性信息, 根据两个节点的结构相关性和属性相关性对节点的整体相关性进行评估. 通过设置一个平衡参数α∈[0,1],vs,i与vt,j的整体相关性定义为
X(vs,i,vt,j)=αXA(vs,i,vt,j)+(1-α)XL(vs,i,vt,j|Λ).
(4)
为更有效地学习参数, 本文利用附加约束指导优化, 相应的带约束损失函数表示为

(5)
其中m表示标签的数量,MCi,j表示不同类型节点的约束. 根据给定的必须链接集Ms,t和不能链接集Cs,t, 当Mst,i,j=1时,MCi,j=1; 当Cst,i,j=1时,MCi,j=0,Xi,j=X(vs,i,vt,j). 这些约束以及对同一类型节点的约束, 也可以用于指导协同聚类.
2.3 半监督协同聚类
本文设计了具有正交限制的半监督非负矩阵三因子分解, 以同时对不同类型的节点进行聚类:

(6)

2.4 联合优化
给定不同类型的节点Vs和Vt, 目标是利用结构信息和属性信息以及一些约束同时对Vs和Vt进行聚类. 为在该模型中同时优化协同聚类和相关性度量, 本文设计一个联合模型学习相应的参数, 包括元路径的权重Λ以及聚类分布S和T.即将相关性矩阵X视为一个与参数Θ={Λ,A}有关的变量X(Θ), 损失函数表示为
L=L1(Θ)+L2(Θ)+γ(‖Θ‖2).
(7)
在SCCAIN中, 使用迭代更新方法学习参数Θ和(S,W,T), 并且每次迭代均由以下两个步骤组成.
1) 用固定的Θ更新S,W,T.给定Θ, 该步骤的主要目标是选择半监督协同聚类模型的解(S,W,T). 有固定的X, 则L可表示为
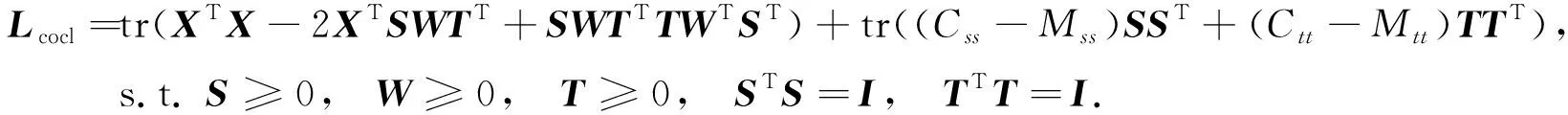
(8)
在这个函数中有3个参数带有约束, 分别固定其中两个参数优化另一个参数:
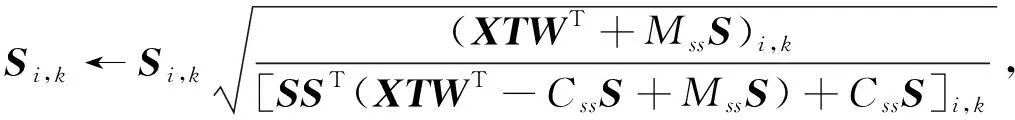
(9)
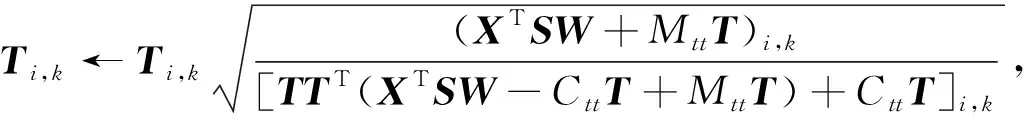
(10)
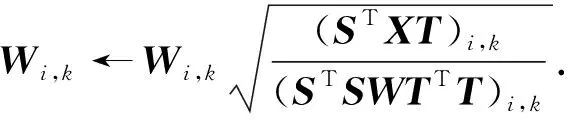
(11)
为获得准确的S,W,T, 迭代更新这3个参数, 直到它们稳定为止. 在更新过程完成后, 固定S,W,T以优化相关性度量.
2) 用固定的S,W,T更新Θ.对于固定的S,W,T,L是Θ={Λ,A}的函数, 全局损失函数等价于
Lrele=‖X(Θ)-SWTT‖2+γ(‖Θ‖2),
(12)
其中X(Θ)由式(4)和参数Θ计算得出,SWTT为固定值. 此外, 考虑到Λ≥0, 本文用max{0,λP}更新λP.
最后, 分别从优化后的S和T获得源节点Gs的聚类和目标节点Gt的聚类. 其中,

相应的算法描述如下.
算法1
输入: 不同类型的节点Vs和Vt;
输出: 元路径的权重Λ以及聚类分布S和T;
步骤1) 初始化相应参数γ
步骤2) do
步骤3) 固定Θ更新S,W,T
步骤4) 根据式(7)计算损失函数
步骤5) until收敛
步骤6) do
步骤7) 固定S更新Θ,W,T
步骤8) 根据式(7)计算损失函数
步骤9) until收敛
步骤10) do
步骤11) 固定W更新S,Θ,T
步骤12) 根据式(7)计算损失函数
步骤13) until收敛
步骤14) do
步骤15) 固定T更新S,W,Θ
步骤16) 根据式(7)计算损失函数
步骤17) until收敛
步骤18) 从优化后的S和T获得源节点Gs的聚类和目标节点Gt的聚类.
3 实 验
3.1 数据集和指标
表1列出了3个公共数据集的信息, 即Aminer,DBLP和一个Alibaba推荐数据集.

表1 数据集信息
1) Aminer数据集是一个公共基准数据集, 由作者(A)、论文(P)和会议(C)三种类型的节点组成, 相应的关系包括“发布”(P-C)、“参与”(A-C)和“写”(A-P). 有5个主要研究领域: 数据挖掘、医学信息学、理论、可视化和数据库, 每个节点都被分配到一个特定的领域. 这里专注于同时对作者和会议进行聚类, 基于A-P-C,A-P-A-P-C和A-P-C-P-A-P-C三个元路径计算结构相关性. 作者和会议的属性都是相关的论文摘要, 利用doc2vec将文本建模为密集向量.
2) DBLP数据集是一个公共子网络, 涉及4个研究领域的主要会议: 数据库、数据挖掘、人工智能和信息检索. 有4种类型的节点: 作者(A)、论文(P)、会议(C)和主题(T). 在该网络中, 也关注作者和会议的协同聚类. 基于A-P-C,A-P-T-P-C和A-P-A-P-C三个元路径计算结构相关性. 这里将在20个会议上由作者撰写的论文数量设置为作者的属性, 并将通过元路径C-P-A-P-C的链接数量设置为会议的属性.

3.2 实验设置
首先将SCCAIN与其他三种协同聚类方法和两种图嵌入方法进行比较; 然后通过比较SCCAIN及其改进版本SCCAIN(L)和SCCAIN(A)分析属性和结构的贡献, 其中前者专注于属性, 而后者专注于结构[12].
DNMTF是一种矩阵三因子分解方法, 可在协同聚类时同时优化矩阵因子分解和图对偶正则化. 为公平比较, 将节点的k最近邻和成对约束都设置为对偶正则化. 这里利用属性HINs中的链接作为输入矩阵. CPSSCC是一种半监督协同聚类方法, 该方法同时利用行约束投影和列约束投影在低维空间中引导聚类源节点和目标节点. ONMTF(HS)是一个非负矩阵三因子分解, 与文献[13]中提出的传统ONMTF不同, 本文利用多个元路径的平均相关性作为相似度矩阵, 并在训练过程中结合成对约束讨论学习相关性度量的有效性. GCN(K)是一种流行的属性图嵌入学习方法, 该方法聚合图信息以重建节点嵌入, 利用监督信息生成节点的基本嵌入, 并采用K均值方法分别对每种类型的节点进行聚类. H2V(K)是一种具有K均值的异构图嵌入模型, H2V根据异构边缘对邻居进行采样, 并学习节点和边缘的嵌入. 在该模型中, 将成对约束整合到图中以进行公平比较[14].
对于SCCAIN, 将学习率设为0.001, 最大迭代次数设为200,γ设为0.01. 利用Adam最小化L1的损失. 由于必须链接和不能链接对是作为监督信息提供的, 因此可通过交叉验证调整α. 对于Aminer,DBLP和Alibaba数据集, 本文分别生成固定数量的必须链接和不能链接的邻居作为总约束, 然后采样2.5%,5%,7.5%,10%的约束进行学习. 基线和SCCAIN都运行10次, 并将平均值报告为性能. 采用标准化互信息NMI∈[0,1]和纯度Purity∈[0,1]作为度量指标, NMI或Purity值越大, 表示性能越好.
3.3 对比分析
表2列出了3个不同尺度数据集上的NMI和Purity值. 对于DBLP和Aminer, 源节点和目标节点分别表示作者和会议; 对于阿里巴巴, 源节点和目标节点分别表示用户和项目. 本文比较了所提出方法在源节点和目标节点聚类上的性能. 图3为协同聚类可视化, 用于描述检测异构集群之间潜在关联的性能.
3.3.1 协同聚类的性能
由表2可见, SCCAIN对于3个数据集均达到最佳性能. 与DNMTF,CPSSCC,ONMTF(HS)相比, 本文主要的改进为可学习的整体相关性; 与GCN(K)和H2V(K)相比, 本文方法是一个同时考虑属性和结构的HINs统一模型. 此外, 由于该网络的稀疏性, DNMTF和CPSSCC在Alibaba数据集上的表现较差.
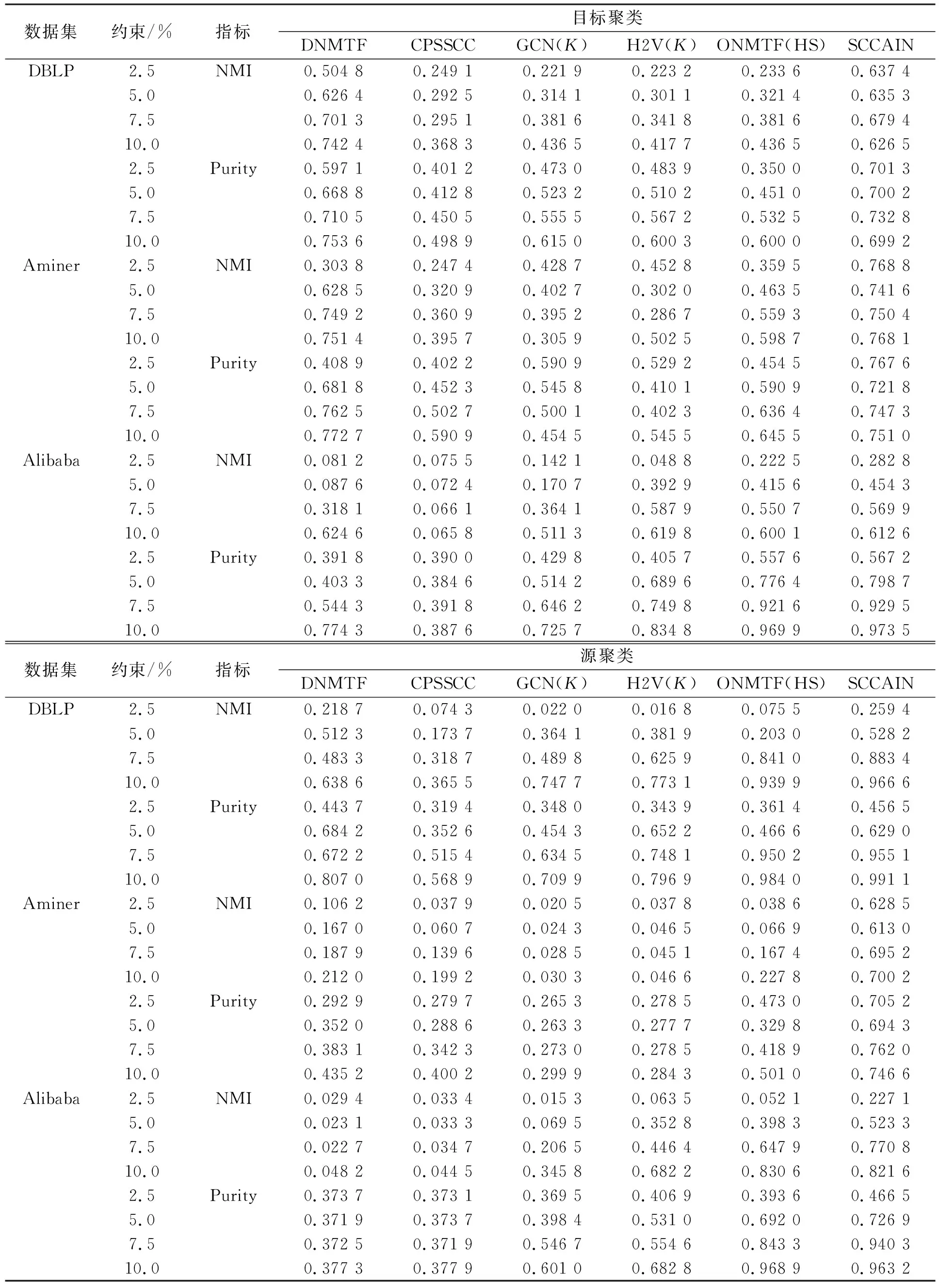
表2 3个不同尺度数据集上的NMI和Purity值
在半监督的情况下, 即存在约束率条件下, SCCAIN在源节点的聚类和目标节点的聚类性能比多数方法有明显优势, 表明SCCAIN在没有太多约束的情况下能极大提升聚类效果. 但其他一些模型, 如GCN(K)和DNMTF, 其性能在很大程度上依赖于监督信息的规模, 且其增长速度慢于SCCAIN. 与采用静态相关性的ONMTF(HS)相比, SCCAIN由于采用了自适应总体相关性度量, 因此其在半监督条件下即可得到良好的聚类性能.
3.3.2 协同聚类可视化
本文模型是同时聚类不同类型的节点, 可通过设置Aminer数据集上的协同聚类作为例子分析这些聚类的相关性. 由图3可见, 根据作者的聚类和会议的聚类, 重新排列了DNMTF,ONMTF(HS),SSCAIN的关联矩阵, 然后显示相应的矩阵可视化, 色块越深表示聚类的相关性越高. 通过比较图3(A)~图3(C)中的块可见, SCCAIN由于明显的块而具有更好的检测不同类型聚类相关性的能力, 这有助于将这些信息用于推荐系统和其他一些有价值的任务.

图3 具有10%约束的Aminer数据集上协同聚类的相关性Fig.3 Correlation of collaborative clustering on Aminer data set with 10% constraint
3.4 模型分析
3.4.1 消融性
本文将SCCAIN与SCCAIN(L)和SCCAIN(A)的性能进行比较, 结果如图4所示. 由图4可见, 与SCCAIN(A)和SCCAIN(L)相比, 本文模型在这3个数据集上的表现都更好. 在Aminer数据集和DBLP数据集上, SCCAIN(L)的性能优于SCCAIN(A), 但SCCAIN(A)在Alibaba数据集上更好. 实验结果表明了整合属性信息和结构信息进行协同聚类的有效性. 此外, 尽管SCCAIN具有相似的结构, 但由于其具有自学习元路径权值, 因此比ONMTF(HS)更好.
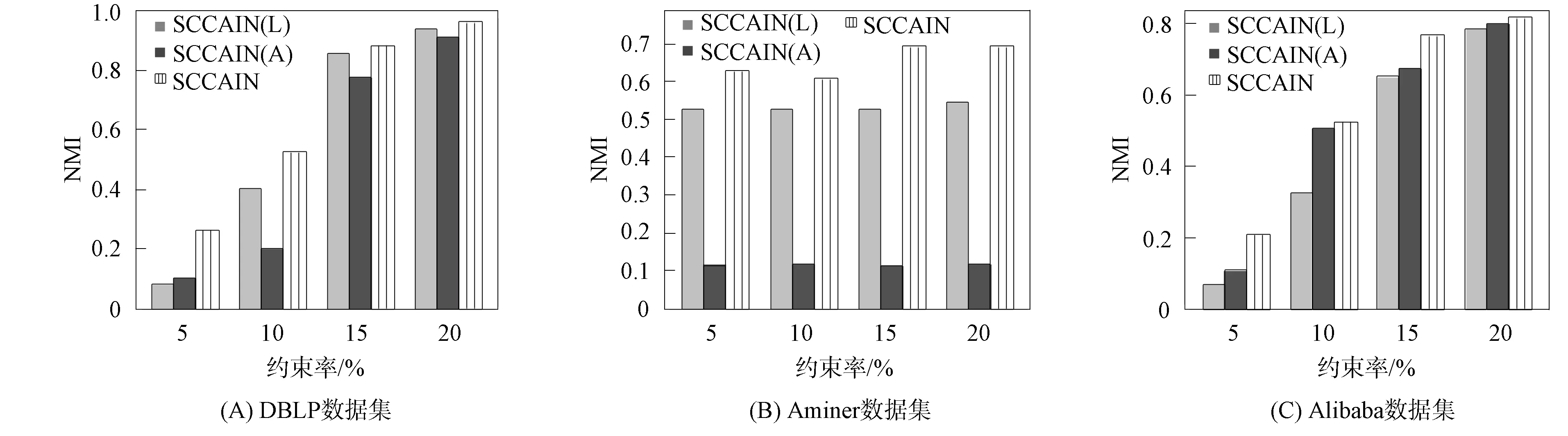
图4 SCCAIN(A),SCCAIN(L),SCCAIN在协同聚类上的NMI性能Fig.4 NMI performance of SCCAIN(A),SCCAIN(L) and SCCAIN in collaborative clustering
3.4.2 收敛性和参数分析
为分析SCCAIN的收敛性, 本文将最大迭代次数从0增加到200, 并通过不同的监督信息展示SCCAIN的NMI值, 结果如图5所示. 由图5可见, 随着3个数据集上监督信息的增加, SCCAIN可更快地收敛, 这验证了监督信息以及优化框架的有效性.
为分析平衡参数α的影响, 将其从0调整为1, SCCAIN的NMI值的变化如图6所示. 由图6可见, 通过比较每个数据集的性能, 发现合适的α可以提高聚类的NMI值. 通过比较不同数据集上的性能趋势, 可观察到α在Aminer数据集上更敏感. 这是因为Aminer数据集上作者和会议的属性是相关抽象向量的平均值. 此外, 若属性相关性过强(即α≥0.5), 则可能很难区分作者或会议. 一方面, 一个会议的论文通常属于多个领域, 因此它们属性向量的平均值在许多不同会议中可能很相似; 另一方面, 由于语料库较小, 因此在建模抽象文本的表示时可能会存在噪声信息. 在DBLP和Alibaba 数据集上, 稳定的性能表明可以更容易地学习节点属性的相关性, 以帮助进行协同聚类.

图5 不同迭代次数的DBLP,Aminer,Alibaba数据集上SCCAIN的NMI值Fig.5 NMI values of SCCAIN on DBLP,Aminer,Alibaba data sets with different iterations
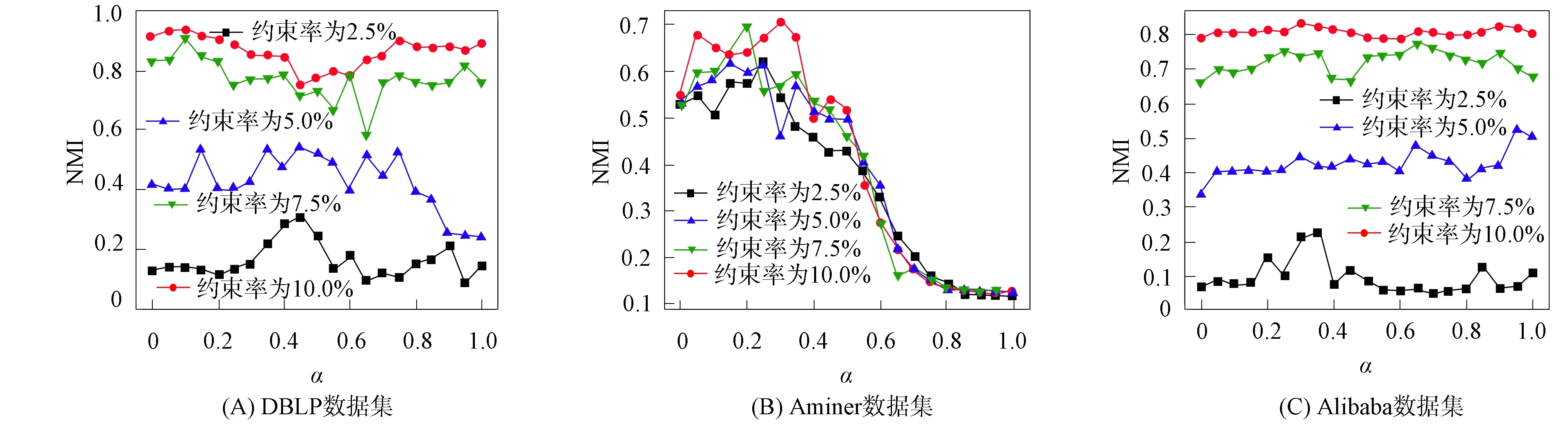
图6 不同α的DBLP,Aminer,Alibaba数据集上SCCAIN的NMI值Fig.6 NMI values of SCCAIN on DBLP,Aminer,Alibaba data sets with different α
综上所述, 为了同时利用属性信息和结构信息实现更精确的协同聚类, 本文提出了一种基于属性异构信息网络的半监督协同聚类框架. 通过分析数据集实验结果表明: 该方法在没有太多约束的情况下能极大提升聚类效果, 实现良好的信息挖掘; 由于采用了自适应总体相关性度量, 且能同时利用属性信息和结构信息, 因此其在半监督条件下即可得到良好的聚类性能; 自学习元路径权值的引入能使本文方法在不同的约束率条件下保持较好的聚类效果, 监督信息的增加可加快收敛速度.

