从属于叶形区域星象函数类的优化性质

由向平, 汤 获, 马丽娜

(赤峰学院 数学与计算机科学学院, 内蒙古 赤峰 024000)

1 引言与基本定义

单复变几何函数论中星象函数优化性质的研究最早始于MacGregor[1], 之后, 对由不同(非)线性算子刻画的单(多)叶函数类和亚纯函数类优化问题的研究得到广泛关注[2-17]. 但上述研究优化结果均基于算子的等价关系. 最近, Tang等[18-20]在未强加任何算子的条件下研究了与正、余弦函数有关的解析函数的优化性质, 从而使优化问题的研究得到进一步发展. 但关于叶形区域解析函数优化问题的研究目前报道较少. 基于此, 本文主要考虑从属于叶形区域星象函数类的优化性质.

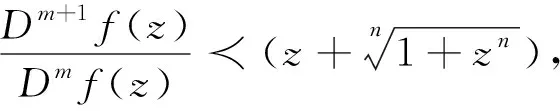
(1)

其中:n∈={1,2,…};m∈0={0}∪; 算子Dn:为Sălăgean算子[4], 定义为

注1在定义1中, 如果选取不同的参数值m,n, 则可得如下函数子类:

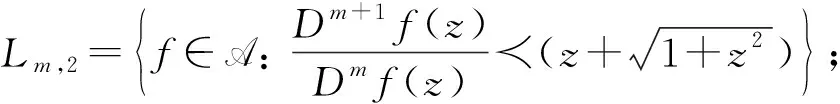
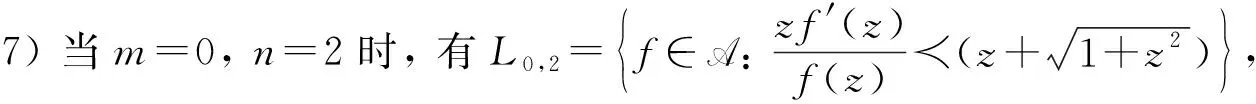
如图1所示;

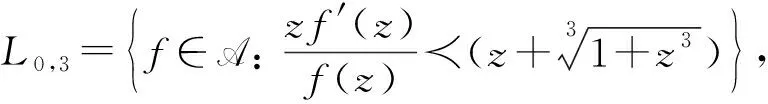
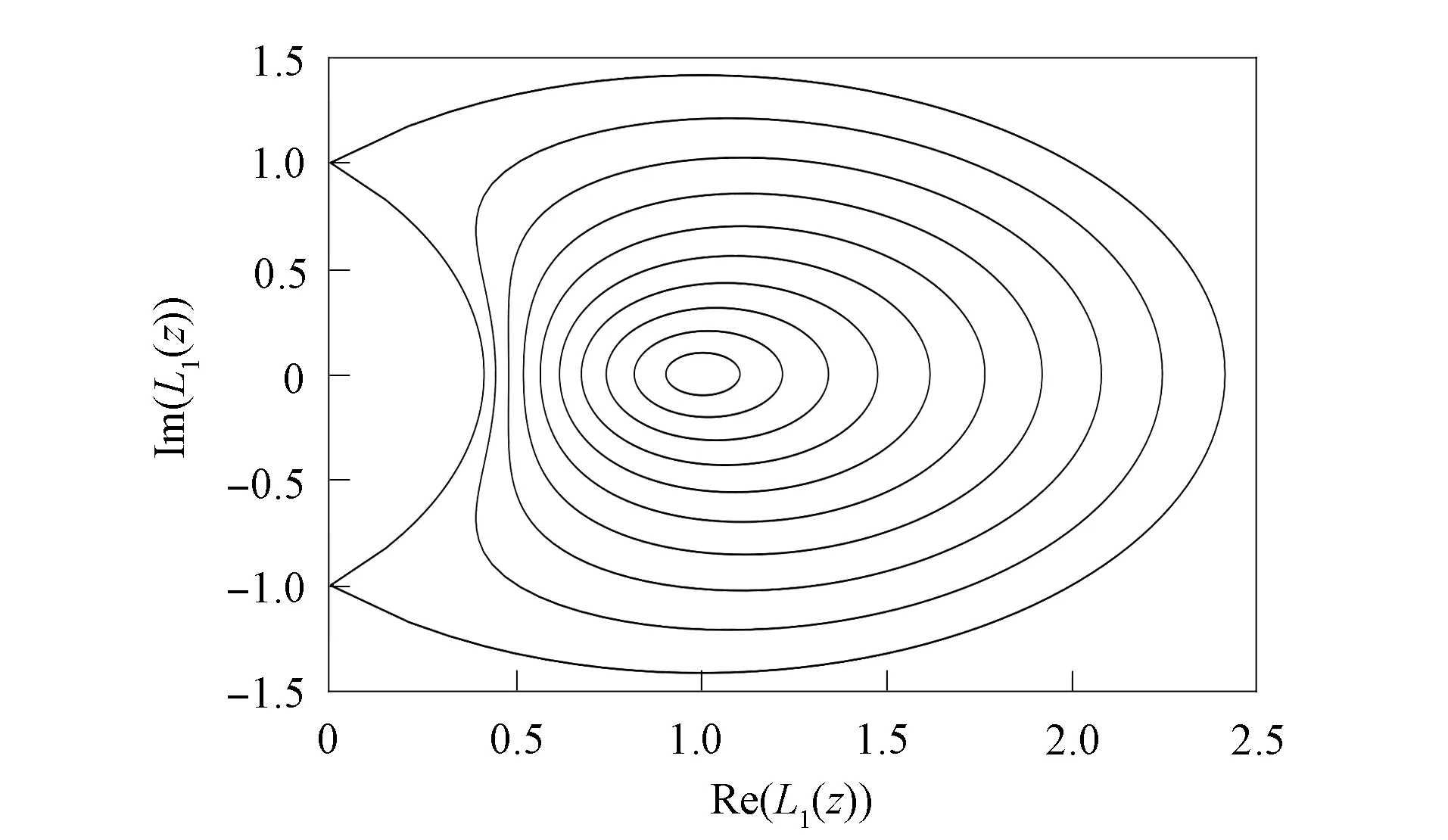
图1 函数的图像

图2 函数的图像

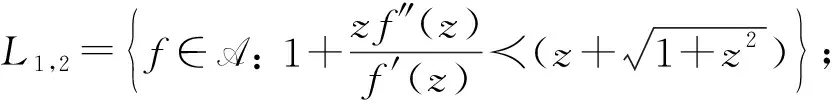
由于综合效率=纯技术效率*规模效率，所以，可以把导致医养结合养老服务投入产出效率低的原因分为两种：一是规模效率低，即养老服务的供给结构不合理，二是纯技术效率较低，即养老服务机构的资源利用率不高，导致投入要素没有得到最有效的使用。因此，需要进一步分析导致9个DEA无效的机构医养结合养老服务效率低的原因。

2 主要结果

则对|z|≤r1, 可得|Dm+1f(z)|≤|Dm+1g(z)|, 其中r1=r1(n)(n∈)为下列方程的最小正根:

(3r-r3)n-(1-r2)n(1+rn)=0.

(2)

证明: 因为g∈Lm,n, 故利用从属关系和式(1), 易得

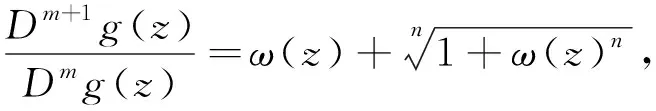
(3)

(4)

的解析函数族[21].

结合式(3)和式(4), 可得

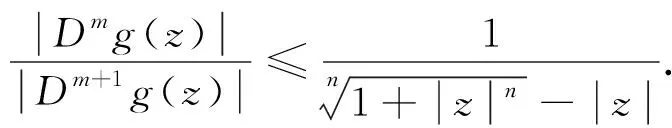
(5)

由于Dmf(z) ≪Dmg(z), 故由优化定义可知

Dmf(z)=φ(z)Dmg(z).

(6)

对式(6)两边关于z求导, 再乘以z得

Dm+1f(z)=zφ′(z)Dmg(z)+φ(z)Dm+1g(z).

(7)

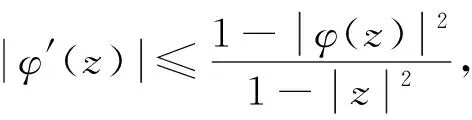
(8)

将式(5)和式(8)代入式(7), 可得

(9)

若设|z|=r, |φ(z)|=ρ(0≤ρ≤1), 则式(9)即化为

|Dm+1f(z)|≤Φ1(r,ρ)|Dm+1g(z)|,

其中

为了确定r1, 可取

其中

易见, 取ρ=1, 则Ψ1(r,ρ)可取到最小值, 即有

min{Ψ1(r,ρ):ρ∈[0,1]}=Ψ1(r,1)=ψ1(r),

其中

又因为ψ1(r)在(0,1)上连续, 且

ψ1(0)=1>0,ψ1(1)=-2<0,

故存在r1, 使得当r∈[0,r1]时, 有ψ1(r)≥0, 这里r1=r1(n)为方程(2)的最小正根. 证毕.

根据定理1及注1, 可得下述推论.

|Dm+1f(z)|≤|Dm+1g(z)| (|z|≤r4),

这里r4是如下方程的最小正根:

6r7+r6-24r5-3r4+26r3+3r2-1=0.

(11)