Heisenberg群中乘积曲面平均曲率流的孤子解

于延华, 封 迪

(东北大学 理学院, 沈阳 110819)

曲面的平均曲率流在数学上被认为是曲面或超曲面沿自身法向量依平均曲率大小的形变[1]. 平均曲率流发展方程在物理学、材料科学和微分几何等领域具有重要作用[1-3]. 目前, 关于曲面平均曲率流在Euclide空间中的研究已有很多成果[2-5]. Cintra等[6]将平均曲率流的研究推广到了三维Heisenberg群上, 并对初始条件是直纹面的平均曲率流进行了分类. Heisenberg群的运算具有非交换性, 该性质使得曲面平均曲率流的性质与Euclide空间完全不同, 结论也更丰富.

本文在三维Heisenberg群中讨论初始条件是乘积面积的平均曲率流孤子解问题. 将三维Heisenberg群中的等距变换群作用在乘积曲面上, 得到随时间变化的单参数曲面族, 并进一步给出该曲面平均曲率流的发展方程及其性质. 若无特殊说明, 本文所有的求和形式都约定采用Einstein求和记号,Ci(i∈)表示常数，H仅表示3维Heisenberg群.

1 预备知识

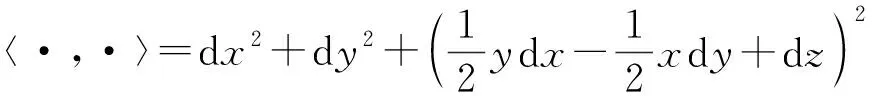
[e1,e2]=e3, [e1,e3]=0, [e2,e3]=0.

由标架{e1,e2,e3}可得H上一组左不变标准正交基{E1,E2,E3}：

用×表示定义在其上的外积运算, 则E1=E2×E3,E2=E3×E1,E3=E1×E2.

设M是一个2维的光滑流形, 坐标是(x1,x2). 设φt(x1,x2):M×I→H,I=[0,T), 则φt是H中一族参数为t的光滑浸入超曲面{Mt}的位置向量, 初始条件为φ0=φ.Mt的第一基本形式与第二基本形式分别为

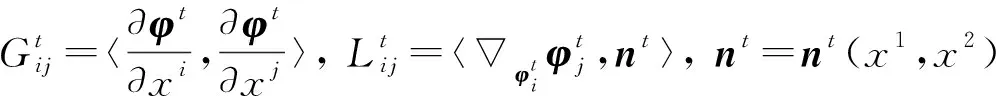
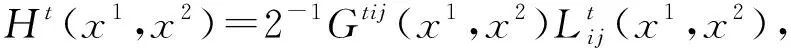
2 基本概念

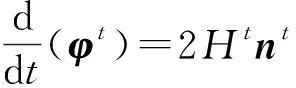
三维Heisenberg群H的等距变换群对应的李代数(记作IsoH)有如下4个基底：

对于单参数等距变换ψt, 记X为由这4个基底组成的李代数, 则基底可生成如下曲面[11]：

令初始条件φ0(u,v)为由光滑函数f(u),g(v)生成的乘积曲面, 且表达式为φ(u,v)=(u,v,f(u)g(v)). 则ψt(φ(u,v))有如下4种形式：

3 主要结果

(5)

证明： 直接计算可得

曲面的切向量为

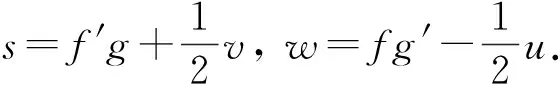
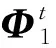
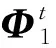
代入平均曲率流的发展方程, 可得ε′(t)=A, 其中A是一个非零常数, 即ε(t)=At.

由定理1可得如下推论：

推论1在X1作用下乘积曲面的平均曲率流随时间运动的函数ε(t)是一个线性函数, 且平均曲率流的存在时间是[0,+∞).

证明： 若曲面存在极小解, 则该极小解必然满足方程组：

因为A≠0成立, 所以方程组的表达式可进一步写为

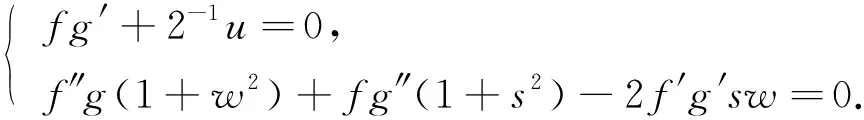
(6)

由方程组(6)中的第一个方程可知

将g的表达式代入方程组(6)中第二个方程可知C2=0, 从而可得解函数为

定理2中极小解对应的曲面几何形状如图1所示.

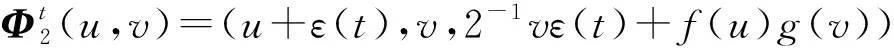
(7)

证明： 计算过程类似定理1, 直接计算可得

代入平均曲率流发展方程可得ε′(t)=A, 且A是一个非零常数.

由定理3可得如下推论：

推论2在X2作用下乘积曲面的平均曲率流随时间运动的函数ε(t)是一个线性函数, 且平均曲率流存在的时间是[0,+∞).

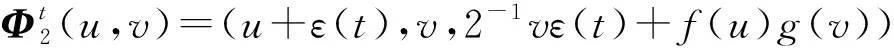
证明： 证明过程类似定理2. 若曲面存在极小解, 则该极小解必然满足方程组：

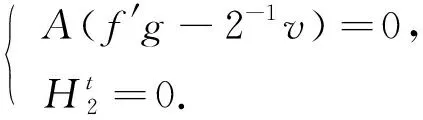
(8)

由方程组(8)可知,

将f的表达式代入方程组(8)可得C4=0, 所以可知解函数为

因此曲面的表达式为Φ2(u,v)=(u,v,2-1uv).

定理4中极小解对应的曲面几何形状如图2所示.

图1 曲面Φ1(u,v)=(u,v,-2-1uv)Fig.1 Surface Φ1(u,v)=(u,v,-2-1uv)

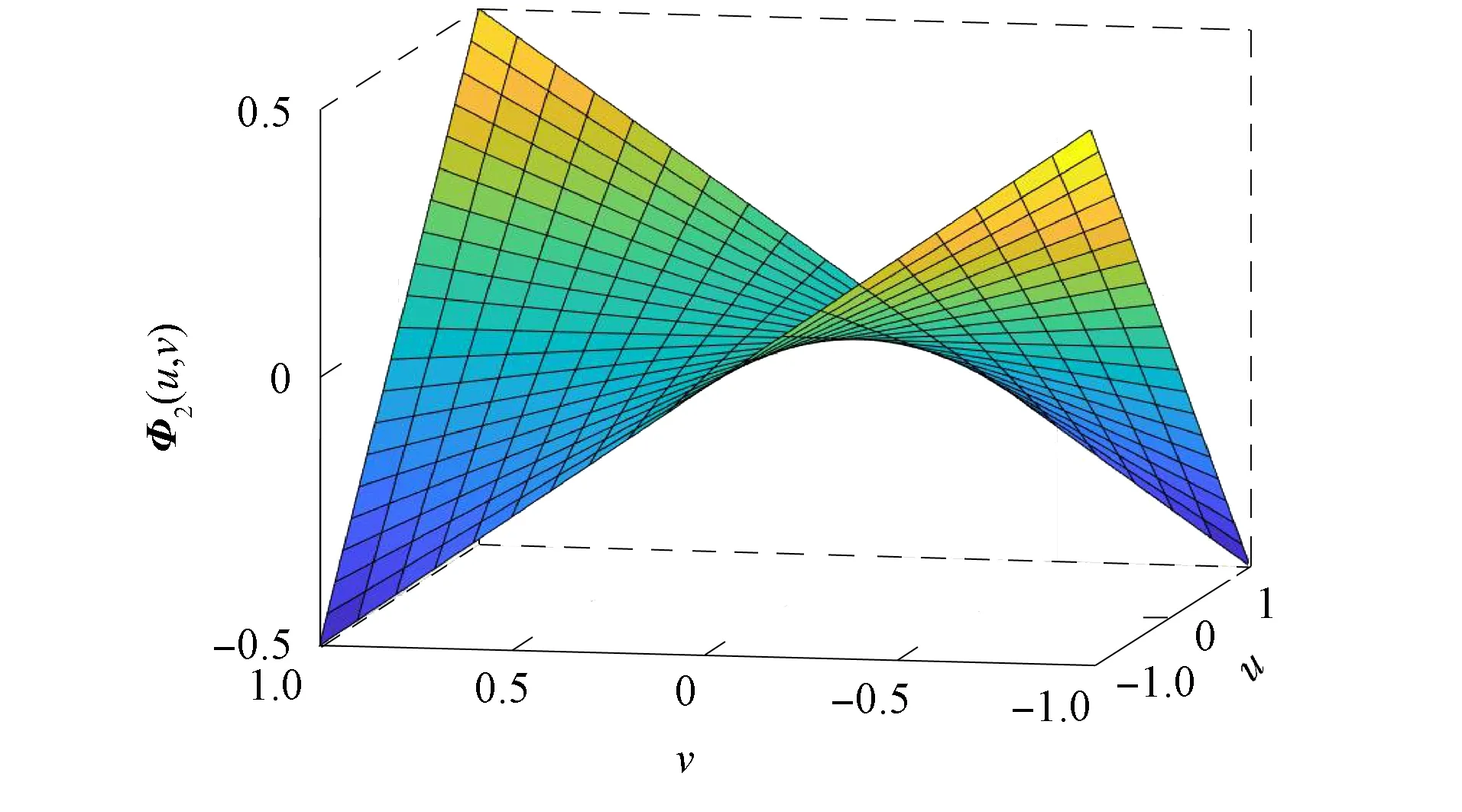
图2 曲面Φ2(u,v)=(u,v,2-1uv)Fig.2 Surface Φ2(u,v)=(u,v,2-1uv)

(9)

证明： 直接计算有

法向量表达式为

又因为

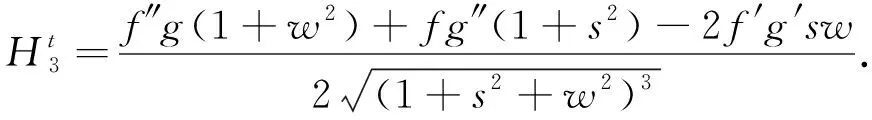
(10)

将式(10)代入式(9)可得ε′(t)=A, 且A是一个非零常数, 因此结论成立.

由定理5可得如下推论：

综上, 本文得到了3种平均曲率流发展方程, 由于所得方程较复杂, 因此本文只对前两种方程求出了极小解, 并未给出第三种方程的极小解.