复杂地形中机载LiDAR点云构建DEM的插值算法对比
李朋飞,张晓晨,严 露,胡晋飞,李 豆,丹 杨
复杂地形中机载LiDAR点云构建DEM的插值算法对比
李朋飞,张晓晨,严 露,胡晋飞※,李 豆,丹 杨
(西安科技大学测绘科学与技术学院,西安 710054)
机载激光雷达(Light Detection and Ranging,LiDAR)可快速、高效的获取大范围地形信息,已成为高精度地形建模的重要数据获取手段。然而,针对复杂地形的机载LiDAR点云构建数字高程模型(Digital Elevation Model,DEM)的插值误差研究缺乏,严重限制了其在土壤侵蚀、开采沉陷等地表过程研究中的应用。该研究基于黄土高塬沟壑区典型地形的机载LiDAR数据,对比了反距离加权(Inverse Distance Weighted,IDW)、克里金(Kriging)、样条函数(Spline)、自然邻域(Natural Neighbor,NN)、趋势面(Trend)、不规则三角网(Triangulated Irregular Network,TIN)等插值算法的插值误差。首先优选了IDW、Kriging、Spline、Trend等4种算法的关键参数,其次分析了不同点云密度和地形下IDW、Kriging、Spline、NN、TIN等5种算法的插值误差及其空间分布。结果表明:1)IDW最优插值参数为权指数1和搜索点数12,Kriging为无方向、高斯函数和搜索点数12,Spline为规则样条函数和搜索点数32,Trend误差达米级,不适用于地形复杂区域。2)当点云密度较小时(1~19点/m2),IDW、Kriging、NN、TIN4种插值方法较为准确地描述地形。当点云密度较大时(39~77点/m2),各个插值方法的DEM空间分布差异不大。3)针对黄土高塬沟壑区复杂地形区域,点云密度越大,DEM的误差越小。陡坡区域DEM的平均绝对误差明显高于缓坡区域,随着点云密度增大,陡坡区域误差明显减小,而缓坡区域变化较小。当点云密度较小时(1~19点/m2),缓坡和陡坡最优插值插值方法分别为NN和TIN;当点云密度较大时(39~77点/m2),缓坡和陡坡最优插值方法均为Spline。研究结果可为机载LiDAR用于地形复杂区域的高精度地形建模与地表过程研究提供依据。
激光雷达;DEM;插值算法;复杂地形;黄土高原
0 引 言
高精度数字高程模型(Digital Elevation Model,DEM)对土壤侵蚀监测[1]、地表沉降监测、径流和土壤侵蚀过程模拟[2]等研究有重要意义。其数据源获取途径包括地形图数字化[3]、传统地面测量[4]、航空摄影测量[5]、光学遥感[6]、合成孔径雷达[7]和激光雷达(Light Detection and Ranging,LiDAR)[8-9]等。相较于其他方法,机载LiDAR可部分穿透植被,快速获取较大范围地表的高精度三维点云,且不受天气影响[10],已成为获取高精度地形建模数据的重要手段[3]。
机载LiDAR获取的原始点云,需经过滤波、分类、插值等过程,才能获得高精度的DEM。其中,插值算法优劣直接影响DEM的精度,进而影响机载LiDAR在地表过程研究中的应用。已有插值算法可分为基于三角网插值与基于规则栅格插值两大类[6]。前者包括不规则三角网(Triangulated Irregular Network,TIN)[11];后者主要包括反距离加权(Inverse Distance Weighted,IDW)[12]、克里金(Kriging)[13]、样条函数(Spline)、自然邻域(Natural Neighbor,NN)、趋势面(Trend)[14]等。近年来,国内外学者已开展点云密度[15-16]、分辨率[17]、插值算法[18]、地形特征[19-20]、滤波算法[21]等对DEM精度影响的研究。然而,较少研究将不同算法用于机载LiDAR点云,并探讨所获得DEM的不确定性(即误差),制约了机载LiDAR在地表过程研究中的应用[22]。
黄土高原地形破碎复杂,复杂的地形条件对高精度DEM的构建提出了挑战。迄今鲜有研究将机载LiDAR用于黄土高原地表过程研究,而机载LiDAR所构建DEM的误差不明,是限制其广泛应用的主要原因之一[10,22]。有效评价不同插值算法在机载LiDAR点云插值中的误差,明确不同地形、点云质量等条件下的最优算法与其误差大小,无疑有助于确定机载LiDAR所能监测的土壤侵蚀过程、地表沉降大小等,进而为机载LiDAR在黄土高原与其他地形复杂区域地表过程研究中的应用奠定基础。
鉴于此,本研究基于机载LiDAR获取的黄土高塬沟壑区典型流域董庄沟的点云数据,对比IDW、Kriging、NN、Spline、TIN、Trend等插值算法生成DEM的误差,探究不同地形、点云密度、插值算法下DEM误差变化规律,为机载LiDAR应用于地形复杂区域地表过程研究提供参考。
1 研究区概况及数据预处理
1.1 研究区概况
董庄沟流域位于甘肃省庆阳市(106°20′~108°45′ E,35°15′~37°10′ N),属于黄土高塬沟壑区(图1)。年降雨量150~750 mm[23-24],年平均气温3.6~14.3 ℃[23],海拔1 200~1 350 m。流域植被以刺槐和旱生灌丛为主[25],土壤类型主要包括风沙土、砂质黄土、典型黄土及黏土[26]。流域侵蚀类型以水力侵蚀和重力侵蚀为主[27],经长期强烈侵蚀,沟壑纵横,梁峁和沟谷地形差异大,地形地貌复杂[28]。
本研究以董庄沟流域沟头附近典型区域为例,筛选地形条件相异的典型地块为研究对象(图1),编号1、2、3地块为缓坡区域,地形起伏及地表粗糙度较低,编号4、5、6、7、8地块为陡坡区域,地形起伏大、地表粗糙度高。同时,编号1~3区和编号4~8区地块内部地形无明显差异。
1.2 数据获取与预处理
利用机载LiDAR系统(SZT-R250)于2019年5月采集目标区域点云数据。机载LiDAR具体参数为:激光发射频率为100 kHz,飞行速度7 km/h,航高50 m,扫描速度为100 000点/s,扫描角为90°~270°,获取的原始点云密度为86点/m2。
采集完成后进行飞行航迹和惯导姿态解算、点云配准和精简、坐标转换等预处理,生成las格式点云数据。以获取的野外实景照片、实地考察结果等为参照,在TerraSolid 2013中,采取手动方式进行滤波获取地面点云,获得的地面点云密度为77点/m2,并采用所获地面点云开展DEM插值与误差检验[11]。
2 研究方法
已有插值方法众多,常用于生态环境研究的方法有IDW、Kriging、NN、Spline、Trend、TIN等[29-30]。因此,利用以上方法插值机载LiDAR点云,探讨不同算法构建DEM的误差,同时分析插值参数、点云密度、地形特征等影响因素对插值方法误差的影响,探讨不同地形条件与点云密度条件下的最优插值算法,为复杂地形条件下的机载LiDAR点云插值提供参考。
2.1 插值方法
反距离加权插值(IDW)以采样点与插值点间的距离为权重计算加权平均值,离插值点越近的采样点权重越大[31-32],当采样点距离插值点距离较远时,权重忽略不计。此方法适用于采样点均匀且密集地区[33]。IDW的主要参数有搜索点数和权指数。
克里金插值法(Kriging)与反距离加权插值方法较为类似,差异主要在于权重选择[34],该方法是采用半变异函数作为权重进行无偏最优估计的一种地统计方法[35]。其优势在于不仅考虑插值点与采样点之间的距离,还兼顾空间分布关系[36],适用于空间相关性较好的采样点,但可能会出现边缘效应[29]。Kriging的关键参数为搜索方向、搜索点数和变异函数。
自然邻域插值(NN)是基于Voronoi结构的插值方法[37],该算法基于泰森多边形,计算各边垂直平分点连线构成的新多边形与原始泰森多边形的比值,并将比值作为权重,因此无需设置插值参数[37]。该方法具有局部性,对局部特性的继承性较好,但局部点缺失时会出现失真[38]。
样条插值(Spline)以最小曲率面逼近各采样点,以获取最佳的平滑曲面[40]。其优势在于能顾及大范围的采样点,生成的曲面光滑[39-40],适用于复杂的高曲率曲面[41],但过于平滑会造成失真。Spline的主要参数有搜索点数和函数类型。
趋势面插值(Trend)以最小二乘原理为基础,用多项式对采样点进行拟合[42],多项式的次数是关键参数。多项式阶数越高,拟合曲面越复杂。趋势面插值有时并非最佳拟合,而是将数据分成区域块[15]。
不规则三角网(TIN)利用一系列点构建三角形[43]。TIN方法的优势在于能够在地形复杂区域保留地表细节,然而,其边缘梯度可能存在突然变化的缺点[29]。
2.2 插值参数优选
所采用的6种插值方法中,TIN和NN无需进行插值参数优选,故仅对IDW、Kriging、Spline、Trend4种算法进行参数优选。待优选参数及取值见表1,通过对比各算法关键参数不同取值下的误差,获取了最优取值。
2.3 点云抽取
本研究所获取机载LiDAR地面点云密度较高(77点/m2),可通过点云抽取获取不同密度的点云,为研究不同密度点云所构建DEM的误差奠定了基础。为使所获点云涵盖不同密度范围,抽取率(所提取点数量占总点数的比例)确定为100%、50%、25%、12.5%、5%、1%,所对应点云密度分别为77、39、19、10、4、1点/m2。
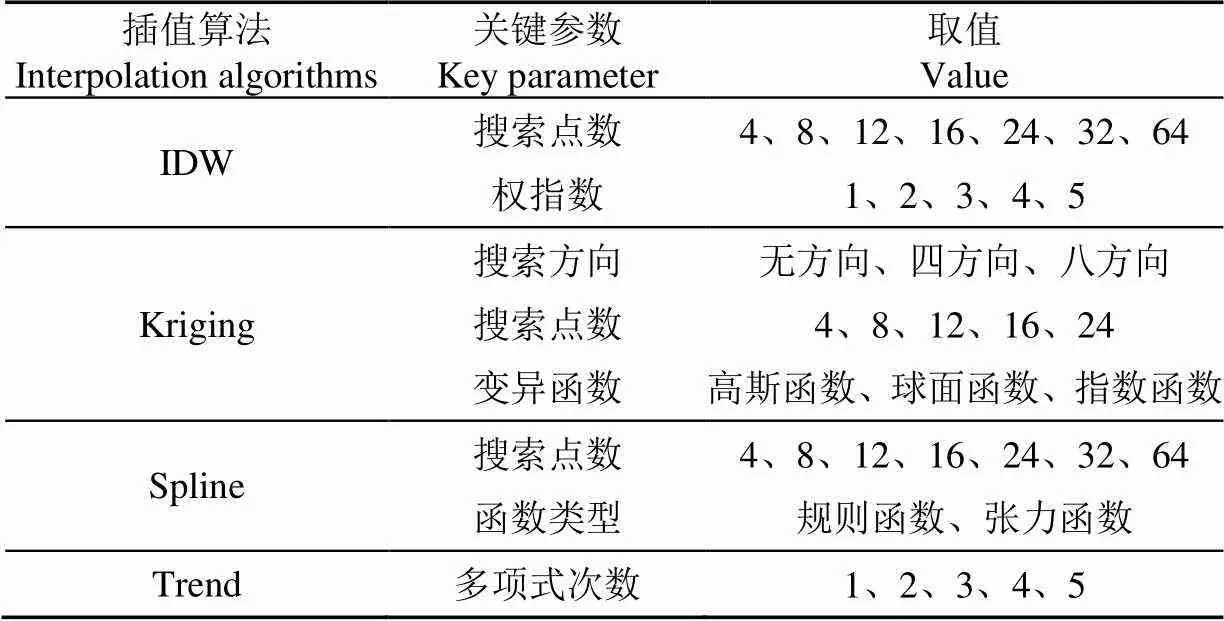
表1 不同插值算法参数待选取值
注:IDW、Kriging、Spline、Trend分别为反距离加权插值、克里金插值、样条插值、趋势面插值算法。
Note: IDW, Kriging, Spline and Trend refer to the inverse distance weighted interpolation algorithm, Kriging interpolation algorithm, Spline interpolation algorithm and Trend interpolation algorithm respectively.
2.4 精度评价
由于研究区域地形复杂,难以到达,同时缺乏地面控制点,因此未能采用地面三维激光扫描仪、GPS等仪器获取更高精度的地面高程数据,用以验证机载LiDAR点云所构建DEM的精度。鉴于此,本文基于机载LiDAR获取的地面点云,利用交叉验证法进行DEM误差分析。交叉验证法为插值精度验证的常用方法,已广泛用于滑坡、气象、地形插值算法的精度研究中[44-45]。在本研究中,将处理完成的地面点云数据随机分为两部分,一部分用于构建0.5 m分辨率DEM,占比99%,剩余1%用于DEM精度验证。首先在所构建DEM中提取与验证点云位置对应的栅格高程值;其次基于所提取栅格高程值与对应验证点云高程值,计算误差指标,评估插值算法的误差。
采用平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Square Error,RMSE)、决定系数(Coefficient of Determination,2)3个指标定量评价插值方法构建DEM的误差。其中MAE和RMSE的值越高,2越低,DEM插值精度越低,误差越大;反之,则DEM插值精度越高,误差越低。
3 结果与讨论
3.1 插值算法的参数优选
由图2a、2b可知,随着搜索点数增大,IDW算法所得DEM的误差先减小后趋于稳定。当搜索点数相同时,误差均随权指数的增大而增加。当权指数为1时,与其他权指数的变化规律不同,搜索点数高于16时,搜索点间的距离变化过大,导致误差值随搜索点数的增加而增加。该结果与陈娟等[46]所得结论一致。当搜索点数小于32时,权指数为1的MAE、RMSE误差值明显低于权指数为2~5,且在搜索点数为12时误差值较小。故本文以权指数为1、搜索点数为12作为IDW插值参数的优选结果。
当搜索方向为无方向时,Kriging算法所得DEM误差随搜索点数的减小呈现先减小后增大的趋势,主要原因可能为研究区地形起伏大,导致地形突变地区误差突增。当搜索方向为四方向和八方向时,MAE、RMSE均随搜索点数的增大而增大,可能由采样点的非均匀分布所致[34]。当搜索点数大于8时,无方向明显优于其余两个搜索方向。故搜索点数8、12、16和无方向为潜在优选参数。随着搜索点数的增加,Kriging的RMSE先减小后增大,在搜索点数为12时达到最小值,而MAE呈缓慢上升态势。与此同时,当函数模型为高斯函数时,误差在3种变异函数中最小,高斯模型在复杂地貌下优于其余两种函数模型。综上,为均衡插值效率和插值精度,选定无方向、高斯函数、搜索点数12作为Kriging插值参数的优选结果。
随着搜索点数增加,Spline算法所得DEM的MAE和RMSE均先减小后稳定。当搜索点数达32时,误差趋于稳定,原因可能为当搜索点数较少时,拟合的曲面存在“失真”,造成估计不准[47]。相同搜索点数下,规则样条函数明显优于张力样条函数,可能由于高阶次导数能更好描述复杂地形变化[40]。综上,在保证插值精度的前提下兼顾插值效率,以规则样条函数和搜索点数32作为Spline插值参数的优选结果。
Trend算法中多项式次数变化对误差有明显影响,当次数大于2时误差值趋于平稳(图2)。将该方法用于黄土高塬沟壑区会导致DEM插值误差过大,平均绝对误差、均方根误差达到米级,因此在后文中不予考虑。
3.2 不同插值算法下DEM质量
当抽取率>50%~100%(点云密度>39~77点/m2)时,IDW、Kriging、Spline、NN、TIN这5种插值方法的DEM空间分布差异较小,未有明显的优劣之分。当抽取率为1%~25%(点云密度1~19点/m2)时,IDW、Kriging、NN、TIN这4种插值方法能够较为准确的描述地形特征,仅有Spline出现“失真”,即部分栅格高程值明显偏离采样点的高程值(如图3a~3d中圆圈所标注区域),表明在点云密度较小时,Spline描述地形的能力较差。
3.3 不同插值算法所构建DEM的误差
3.3.1 整体误差评价
由图4可知,随着点云密度的增大,5种插值方法的MAE和RMSE均先减小后趋于稳定。当抽取率1%~12.5%(点云密度1~10点/m2)时,MAE和RMSE骤减,最大变化量分别为0.232和0.319 m;抽取率>12.5%~25%(点云密度>10~19点/m2)时,MAE和RMSE缓慢减少,最大变化量分别为0.024和0.073 m;抽取率>25%~100%(点云密度>19~77点/m2)时,5种插值方法的MAE和RMSE趋于平稳,最大变化量不足0.011 m。
当抽取率小于12.5%(点云密度小于10点/m2)时,TIN和NN的整体误差明显低于IDW、Kriging、Spline。当抽取率为1%(点云密度为1点/m2)时,TIN的MAE和RMSE最小,分别为0.208和0.298 m;当抽取率为>5%~12.5%(点云密度>4~10点/m2)时,NN的MAE和RMSE最小,分别为0.170~0.175 m和0.259~0.262 m。Polat等以伊斯坦布尔城区为研究区,在0.3点/m2的点云密度下研究发现IDW、NN、Kriging3种插值方法中NN插值效果最好[15],与本研究结果一致,但该研究区域较为平坦,未开展地形复杂区域各算法误差的对比,同时所获取点云密度较低,未能开展较高点云密度下的插值误差分析。
抽取率>12.5%~25%(点云密度>10~19点/m2)时,Spline的MAE和RMSE的变化量分别为0.024和0.073 m,高于其余4种插值方法,说明Spline对点云密度的变化更为敏感。当抽取率高于25%(点云密度>19点/m2)时,5种插值方法构建DEM的误差趋于平缓,且MAE和RMSE变化量均不大于0.011和0.010 m,说明当点云密度足够大时,插值方法对DEM的精度影响较小,同时Spline的整体误差小于其余4种算法,其MAE和RMSE分别为0.164~0.168 m和0.249~0.255 m。
不同的点云密度下,5种插值所得DEM与采样点实测值均有很好的相关性,决定系数2均大于0.99。Habib等以摩洛哥的平原和丘陵为研究区,认为IDW、普通克里金(Ordinary Kriging,OK)、薄板样条插值(Thin Plate Spline,TPS)这3种插值方法的2可达到0.99[48],但需注意,该研究区域为较平坦的平原与丘陵区,并未涉及地形复杂区域;Polat等研究也发现不同抽取率(10%、30%、50%、70%、100%)下的2变化不大[15],但如前所述,与本文不同,其研究区较平坦且点云密度较低。此外,本文中各插值方法在不同抽取率下2未有明显变化,可能原因之一为验证数据和训练数据均由机载LiDAR获取,并未使用更高精度数据(如GPS-RTK)评估DEM构建误差。后续可将GPS-RTK等仪器获取的数据作为验证数据,进一步评估构建DEM的精度。
3.3.2 误差空间分布
以5×5个栅格作为基本单元计算验证点与DEM模型的MAE,获取不同抽取率下各插值算法的DEM误差空间分布特征(图5)。由图5可知,研究区左下方误差相较于右上方整体偏高,同时,编号1~3区DEM误差明显低于编号4~8区,且在点云密度为1点/m2时尤为明显。说明平缓地区的DEM误差低于陡峭区域,且在低点云密度下,二者差异更加明显。
在缓坡区域(编号1~3区)随着点云密度增大,误差减小,当点云密度高于10点/m2时,5种插值算法的误差减小幅度低,表明缓坡区域对点云密度变化的敏感度较低,亦表明当缓坡区域点云密度高于10点/m2,点云密度的增加对降低DEM误差作用不明显。当点云密度为1~19点/m2时,编号1~3区NN生成 DEM误差低于其余4种算法,MAE为0.049~0.171 m;点云密度>39~77点/m2时,Spline误差值最小,MAE为0.010~0.123 m。
在陡坡区域(编号4~8区),插值误差随点云密度的增大亦减小,尤其当点云密度从1点/m2升高至4点/m2时5种插值算法的误差成倍减少;当点云密度>4~19点/m2时,各区域插值方法的DEM误差整体减小;当点云密度高于39点/m2时,DEM误差趋于稳定。因此,陡坡区域的点云密度越高,对地形变化复杂的区域细节描述越精确。当点云密度为1~19点/m2时,编号4~8区采用TIN方法的DEM插值误差低于其余4种算法,MAE为0.062~0.776 m;而在点云密度>39~77点/m2时,Spline算法最优,MAE为0.051~0.593 m。
4 结 论
本研究以黄土高塬沟壑区董庄沟流域内典型区域为例,基于机载LiDAR获取的点云,对比了IDW、Kriging、Spline、NN、Trend、TIN等插值算法的插值误差。首先优选了IDW、Kriging、Spline、Trend等4种算法的参数,其次分析了IDW、Kriging、Spline、NN、TIN等5种插值方法在不同点云密度、地形下构建DEM的误差及其分布特征。主要结论如下:
1)针对黄土高塬沟壑区地形复杂区域,IDW、Kriging、Spline插值参数的优选结果分别为:权指数1、搜索点数12;无方向、高斯函数、搜索点数12;规则样条函数和搜索点数32。Trend不适用于地形复杂区域。所得最优参数对地形复杂区域插值参数初步选取有参考意义,但在其他地区应用时,仍需进一步验证调整,以获取最优参数。
2)当点云密度较小时(1~19点/m2),IDW、Kriging、NN、TIN等4种插值方法较为准确地描述地形,Spline所得DEM存在失真。当点云密度较大时(39~77点/m2),各个插值方法的DEM空间分布差异不大。
3)针对黄土高塬沟壑区复杂地形区域,点云密度越大,DEM的误差越小。随着点云密度增大,陡坡区域误差明显减小,而缓坡区域变化较小。当点云密度较小时(1~19点/m2),缓坡和陡坡最优插值插值方法分别为NN和TIN;当点云密度较大时(39~77点/m2),缓坡和陡坡最优插值方法均为Spline。
[1] Li A, Zhang X C, Liu B Y. Effects of DEM resolutions on soil erosion prediction using Chinese Soil Loss Equation[J]. Geomorphology, 2021, 384: 107706.
[2] Bircher P, Liniger H P, Prasuhn V. Comparing different multiple flow algorithms to calculate RUSLE factors of slope length (L) and slope steepness (S) in Switzerland[J]. Geomorphology, 2019, 346: 106850.
[3] 李振洪,李鹏,丁咚,等. 全球高分辨率数字高程模型研究进展与展望[J]. 武汉大学学报:信息科学版,2018,43(12):1927-1942.
Li Zhenhong, Li Peng, Ding Dong, et al. Reacher progress of global high resolution digital elevation models[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 1927-1942. (in Chinese with English abstract)
[4] Zhu Y, Liu X, Zhao J, et al. Effect of DEM interpolation neighbourhood on terrain factors[J]. International Journal of Geo-Information, 2019, 8(1): 1-30.
[5] 刘燕,杨树文,薛理,等. 参考地理数据的大比例尺影像无控定位[J]. 测绘通报,2020(8):18-22,27.
Liu Yan, Yang Shuwen, Xue Li, et al. Uncontralled positioning of large-scale image with reference to geographic data[J]. Bulletin of Surveying and Mapping, 2020(8): 18-22, 27. (in Chinese with English abstract)
[6] 江海英,贾坤,赵祥,等. 山地叶面积指数反演理论、方法与研究进展[J]. 遥感学报,2020,24(12):1433-1449.
Jiang Haiying, Jia Kun, Zhao Xiang, et al. Review on the theory, method, and research progress of leaf area index estimation in mountainous areas[J]. Journal of Remote Sensing, 2020, 24(12): 1433-1449. (in Chinese with English abstract)
[7] 何永红,靳鹏伟,舒敏. 基于多尺度相关性分析的InSAR对流层延迟误差改正算法[J]. 地球信息科学学报,2020,22(9):1878-1886.
He Yonghong, Jin Pengwei, Shu Min. InSAR tropospheric delay error correction algorithm based on multi-scale correlation analysis[J]. Journal of Geo-Information Science, 2020, 22(9): 1878-1886. (in Chinese with English abstract)
[8] 张凡,李华山,江涛. 基于布模拟算法在LiDAR点云中生成数字高程模型[J]. 激光与光电子学进展,2020,57(13):114-121.
Zhang Fan, Li Huashan, Jiang Tao. Generating Digital Elevation Model in Lidar point cloud based on cloth distributed simulation algorithm[J]. Laser and Optoelectronics Progress, 2020, 57(13): 114-121. (in Chinese with English abstract)
[9] Hui Z, Jin S, Xia Y, et al. Wood and leaf separation from terrestrial LiDAR point clouds based on mode points evolution[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2021, 178: 219-239.
[10] 李豆,李朋飞,穆兴民,等. 机载LiDAR测量复杂地形中滤波算法的比较研究[J]. 水土保持研究,2021,28(4):171-178.
Li Dou, Li Pengfei, Mu Xingmin, et al. Accuracy of airborne Lidar point cloud filtering for areas with complex terrain[J]. Research of Soil and Water Conservation, 2021, 28(4): 171-178. (in Chinese with English abstract)
[11] 岳彦利,罗明良,张斌. 干热河谷冲沟DEM插值误差的空间分布研究[J]. 武汉大学学报:信息科学版,2018,43(7):1122-1128.
Yue Yanli, Luo Mingliang, Zhang Bin. Study on spatial distribution of DEM interpolation errors in the gully of dry-hot valley[J]. Geomatics and Information Science of Wuhan University, 2018, 43(7): 1122-1128. (in Chinese with English abstract)
[12] 柴华彬,胡吉彪,耿思佳. 融合实测数据的地表沉降SBAS-InSAR监测方法[J/OL]. 煤炭学报,2021-01-08 [2021-07-30]. https://doi.org/10.13225/j.cnki.jccs.ST20.1563.
Chai Huabin, Hu Jibiao, Geng Sijia. SBAS-InSAR monitoring method of ground subsidence in mining areas by fusion with measured data[J/OL]. Journal of China Coal Society, 2021-01-08[2021-07-30]. https://doi.org/10.13225/ j.cnki.jccs. ST20.1563. (in Chinese with English abstract)
[13] Wang Y, Xiao Z, Aurangzeib M, et al. Effects of freeze-thaw cycles on the spatial distribution of soil total nitrogen using a geographically weighted regression kriging method[J]. Science of the Total Environment, 2020, 763: 142993.
[14] 刘炜,焦树林,李银久,等. 喀斯特地表植被覆盖变化及其与气候因子相关性分析[J]. 水土保持研究,2021,28(3):203-215.
Liu Wei, Jiao Shulin, Li Yinjiu, et al. Analysis on the of correlation between vegetation cover of land surface and climatic factors in Karst area[J]. Research of Soil and Water Conservation, 2021, 28(3): 203-215. (in Chinese with English abstract)
[15] Polat N, Uysal M, Toprak A S. An investigation of DEM generation process based on LiDAR data filtering, decimation, and interpolation methods for an urban area[J]. Measurement, 2015, 75: 50-56.
[16] 周建红,杨彪,王华,等. 长江中下游河道岸滩低空机载LiDAR点云地形滤波算法[J]. 河海大学学报:自然科学版,2019,47(1):26-31.
Zhou Jianhong, Yang Biao, Wang Hua, et al. Filtering algorithm of the low-attitude airborne LiDAR point clouds for topographic survey of the middle-lower Yangtze River riparian zone[J]. Journal of Hohai University: Natural Science Edition, 2019, 47(1): 26-31. (in Chinese with English abstract)
[17] López-Vicente M, Álvarez S. Influence of DEM resolution on modelling hydrological connectivity in a complex agricultural catchment with woody crops[J]. Earth Surface Processes and Landforms, 2018, 43: 1403-1415.
[18] Habib M. Evaluation of DEM interpolation techniques for characterizing terrain roughness[J]. Catena, 2021, 198: 105072.
[19] 熊礼阳,汤国安,杨昕,等. 面向地貌学本源的数字地形分析研究进展与展望[J]. 地理学报,2021,76(3):595-611.
Xiong Liyang, Tang Guoan, Yang Xin, et al. Geomorphology-oriented digital terrain analysis: progress and perspectives[J]. Acta Geographica Sinica, 2021, 76(3): 595-611. (in Chinese with English abstract)
[20] Yang D, Qiu H, Hu S, et al. Influence of successive landslides on topographic changes revealed by multitemporal high-resolution UAS-based DEM[J]. Catena, 2021, 202: 105229.
[21] Zeybek M , Sanlioglu I . Point cloud filtering on UAV based point cloud[J]. Measurement, 2019, 133: 99-111.
[22] Okyay U, Telling J, Glennie C L, et al. Airborne lidar change detection: An overview of Earth sciences applications[J]. Earth-Science Reviews, 2019, 198: 102929.
[23] 侯青青,裴婷婷,陈英,等. 1986—2019年黄土高原干旱变化特征及趋势[J]. 应用生态学报,2021,32(2):649-660.
Hou Qingqing, Pei Tingting, Chen Ying, et al. Variations of drought and its trend in the Loess Plateau from 1986 to 2019[J]. Chinese Journal of Applied Ecology, 2021, 32(2): 649-660. (in Chinese with English abstract)
[24] 胡宇美,马理辉,李蕊,等. 黄土高原地区森林生态系统地下生物量的因素分析[J/OL]. 生态学报,2021-07-05 [2021-07-30]. http://kns.cnki.net/kcms/detail/11.2031.Q.20210705.1534.040.html.
Hu Yumei, Ma Lihui, Li Rui, et al. Factor analysis of underground biomass in forest ecosystem on the Loess Plateau[J/OL]. Acta Ecologica Sinica, 2021-07-05 [2021-07-30]. http://kns.cnki.net/kcms/detail/11.2031.Q.20210705. 1534.040.html. (in Chinese with English abstract)
[25] 赵广举,穆兴民,田鹏,等. 黄土高原植被变化与恢复潜力预测[J]. 水土保持学报,2021,35(1):205-212.
Zhao Guangju, Mu Xingmin, Tian Peng, et al. Prediction of vegetation variation and vegetation restoration potential in the Loess Plateau[J]. Journal of Soil and Water Conservation, 2021, 35(1): 205-212. (in Chinese with English abstract)
[26] 李婷,吕一河,任艳姣,等. 黄土高原植被恢复成效及影响因素[J]. 生态学报,2020,40(23):8593-8605.
Li Ting, Lü Yihe, Ren Yanjiao, et al. Gauging the influencing of vegetation restoration and the influence factors in the Loess Plateau[J]. Acta Ecologica Sinica, 2020, 40(23): 8533-8605. (in Chinese with English abstract)
[27] Zhao G J, Mu X M, Wen Z, et al. Soil erosion, conservation, and Eco-environment changes in the Loess Plateau of China[J]. Land Degradation & Development, 2013, 24(5): 499-510.
[28] Li P F, Hao M K, Hu J F, et al. Spatiotemporal patterns of hillslope erosion investigated based on field scouring experiments and terrestrial laser scanning[J]. Remote Sensing, 2021, 13(9): 1674.
[29] Li J, Heap A D. Spatial interpolation methods applied in the environmental sciences: A review[J]. Environmental Modelling & Software, 2014, 53: 173-189.
[30] Li J, Heap A D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors[J]. Ecological Informatics, 2011, 6(3/4): 228-241.
[31] 徐翔,许瑶,孙青青,等. 复杂山地环境下气候要素的空间插值方法比较研究[J]. 华中师范大学学报:自然科学版,2018,52(1):122-129.
Xu Xiang, Xu Yao, Sun Qingqing, et al. Comparison study on meteorological spatial interpolation approaches in kangdian region of China[J]. Journal of Central China Normal University: Natural Science Edition, 2018, 52(1): 122-129. (in Chinese with English abstract)
[32] Fan J L, Wu L F, Zheng J, et al. Medium-range forecasting of daily reference evapotranspiration across China using numerical weather prediction outputs downscaled by extreme gradient boosting[J]. Journal of Hydrology, 2021, 601: 126664.
[33] 张孟丹,余钟波,谷黄河,等. 无定河流域降水量空间插值方法比较研究[J]. 人民黄河,2021,43(4):30-37,99.
Zhang Mengdan, Yu Zhongbo, Gu Huanghe, et al. Comparative study on spatial interpolation methods of rainfall in the Wuding River Basin[J]. Yellow River, 2021, 43(4): 30-37, 99. (in Chinese with English abstract)
[34] 蒋伟达,孙永福,刘绍文,等. 基于IDW的埕岛海域水下三角洲地形演变[J]. 海洋科学进展,2020,38(4):697-707.
Jiang Weida, Sun Yongfu, Liu Shaowen, et al. Terrain evolution of subaqueous delta in Chengdao sea area based on IDW[J]. Advances in Marine Science, 2020, 38(4): 697-707. (in Chinese with English abstract)
[35] Chen C, Hu B, Li Y. Easy-to-use spatial Random Forest-based downscaling-calibration method for producing high resolution and accurate precipitation data[J]. Hydrology and Earth System Sciences Discussions, 2021, 332: 1-50.
[36] Nath H, Islam M R. Spatial variability of metal elements in soils of a waste disposal site in Khulan: A geostatistical study[C]// Proceedings of the 5th International Conference on Advances in Civil Engineering (ICACE 2020). Berlin: Springer, 2021.
[37] 杨秋丽,魏建新,郑江华,等. 离散点云构建数字高程模型的插值方法研究[J]. 测绘科学,2019,44(7):16-23.
Yang Qiuli, Wei Jianxin, Zheng Jianghua, et al. Comparison of interpolation methods of digital elevation model using discrete point cloud data[J]. Science of Surveying and Mapping, 2019, 44(7): 16-23. (in Chinese with English abstract)
[38] 冯波,陈明涛,岳冬冬,等. 基于两种插值算法的三维地质建模对比[J]. 吉林大学学报:地球科学版,2019,49(4):1200-1208.
Feng Bo, Chen Mingtao, Yue Dongdong, et al. Comparison of 3D geological modeling based on two different interpolation algorithms[J]. Journal of Jilin University: Earth Science Edition, 2019, 49(4): 1200-1208. (in Chinese with English abstract)
[39] 张锦明,游雄,万刚. 径向基函数算法中插值参数对DEM精度的影响[J]. 武汉大学学报:信息科学版,2013,38(5):608-612.
Zhang Jinming, You Xiong, Wan Gang. Effects of interpolation parameters in Multi-Log Radial Basis Function on DEM accuracy[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 608-612. (in Chinese with English abstract)
[40] 徐洋,战超,王庆,等. 基于海图数据的水下岸坡插值精度分析对比研究[J]. 海洋通报,2019,38(6):632-639.
Xu Yang, Zhan Chao, Wang Qing, et al. A comparative study on interpolation accuracy of underwater slope terrain based on sea chart data[J]. Marine Science Bulletin, 2019, 38(6): 632-639. (in Chinese with English abstract)
[41] Brecheisen Z S, Richter D B. Gully-erosion estimation and terrain reconstruction using analyses of microtopographic roughness and LiDAR[J]. Catena, 2021, 202: 105264.
[42] 崔晓临,程贇,张露,等. 基于DEM修正的MODIS地表温度产品空间插值[J]. 地球信息科学学报,2018,20(12):1768-1776.
Cui Xiaolin, Cheng Yun, Zhang Lu, et al. Spatial interpolation of MODIS land surface temperature products based on DEM correction[J]. Journal of Geo-Information Science, 2018, 20(12): 1768-1776. (in Chinese with English abstract)
[43] 曹林,朱兴洲,代劲松,等. 基于机载小光斑LiDAR数据插值的亚热带森林丘陵地形的误差分析[J]. 南京林业大学学报:自然科学版,2014,38(4):7-13.
Cao Lin, Zhu Xingzhou, Dai Jinsong, et al. Error analysis of DEM interpolation based on small-foolprint airborne Lidar in subtropical hilly forest[J]. Journal of Nanjing Forestry University: Natural Science Edition, 2014, 38(4): 7-13. (in Chinese with English abstract)
[44] 罗路广,裴向军,黄润秋. 强震山区地震滑坡发生概率研究:以九寨沟国家地质公园为例[J]. 岩石力学与工程学报,2020,39(10):2079-2093.
Luo Luguang, Pei Xiangjun, Huang Runqiu. Earthquake- triggered landslide occurrence probability in strong mountainous area: A case study of Jiuzhaigou National Geological Park[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(10): 2079-2093. (in Chinese with English abstract)
[45] Zou W Y, Yin S Q, Wang W T. Spatial interpolation of the extreme hourly precipitation at different return levels in the Haihe River basin[J]. Journal of Hydrology, 2021, 598: 126273.
[46] 陈娟,罗明良,张斌,等. 反距离加权插值参数变化对元谋冲沟DEM构建的影响[J]. 中国水土保持科学,2015,13(1):29-34.
Chen Juan, Luo Mingliang, Zhang Bin, et al. Effects of interpolation parameters in inverse distance weighted method on DEM accuracy in dry-hot valleys of yuanmou[J]. Science of Soil and Water Conservation, 2015, 13(1): 29-34. (in Chinese with English abstract)
[47] 朱海金. 基于不同插值算法生成DEM及对地形因子影响的研究[D]. 福州:福州大学,2013.
Zhu Haijin. Study on Different Interpolation Algorithms to Generate DEM and the Influence of Terrain Factor[D]. Fuzhou: Fuzhou University, 2013. (in Chinese with English abstract)
[48] Habib A, Khoshelham K, Akdim N, et al. Impact of spatial resolution, interpolation and filtering algorithms on DEM accuracy for geomorphometric research: A case study from Sahel-Doukkala, Morocco[J]. Modeling Earth Systems and Environment, 2018, 4(4): 1537-1554.
Comparison of interpolation algorithms for DEMs in topographically complex areas using airborne LiDAR point clouds
Li Pengfei, Zhang Xiaochen, Yan Lu, Hu Jinfei※, Li Dou, Dan Yang
(,,710054,)
Airborne Light Detection and Ranging (LiDAR) technology has widely been used to efficiently acquire terrain data over large areas, particularly providing data sources for the generation of high-resolution Digital Elevation Models (DEMs). However, little was known about the errors in the interpolation of airborne LiDAR point clouds for topographically complex areas, thereby resulting in the less application of airborne LiDAR in the earth surface process. In this study, the errors of six commonly-used DEM interpolations were assessed using the airborne LiDAR point clouds acquired from a topographically complex area in the gullied Loess Plateau, China. Six DEM interpolations included the Inverse Distance Weighted (IDW), Kriging, Spline, Natural Neighbor (NN), Triangulated Irregular Network (TIN), and Trend. Firstly, four parameters were optimized, including IDW, Kriging, Spline, and Trend. Secondly, the optimized algorithms were applied to produce DEMs. Lastly, the errors of DEMs were quantitatively evaluated using mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (2). Results showed that: 1) The optimal values of IDW weights and searching points were 1 and 12, respectively. The optimal parameters for Kriging included non-orientation, Gauss function, and 12 searching points. Spline performed best in regular spline functions and 32 of searching points. Nevertheless, Trend was unsuitable for the topographically complex area, due to the produced DEMs with meter-level errors. 2) In terms of quality, IDW, Kriging, NN, and TIN produced relatively sound DEMs at the 1%-25% subsampling rate (1-19 points /m2), whereas, unreasonable outliers were found in the DEMs produced by Spline. Additionally, there were similar spatial patterns in the DEMs produced by IDW, Kriging, NN, TIN, and Spline, when the subsampling rate was 50%-100% (39-77 points /m2). 3) Excellent relations (2>0.99) were found between the elevation measurements and the DEMs produced using point clouds of different subsampling rates. The average MAE and RMSE of produced DEMs firstly decreased rapidly, and then stabilized, as the point density increased, demonstrating that the reduction of interpolation errors varied slowly, as the point density reached a certain level. TIN produced the lowest error at a 1% subsampling rate (1 points/m2), with the MAE and RMSE of 0.208 and 0.298 m, respectively. At the 5%-12.5% subsampling rate (4-10 points/m2), NN produced the lowest error, where the MAE and RMSE were 0.170-0.175 m and 0.259-0.262 m, respectively. At the >25%-100% subsampling rate (>19-77 points/m2), Spline yielded the lowest error with the MAE and RMSE of 0.164-0.168 and 0.249-0.255 m, respectively. More importantly, the interpolation errors for steep areas were considerably higher than those for gently-sloping areas. The errors for steep areas decreased markedly, while those for gently-sloping areas changed slightly, as the point density increased. NN and TIN were the most suitable interpolation for gently- and steep-sloping areas at the point density of 1-19 points/m2, with the MAE of 0.049-0.171 and 0.062-0.776 m, respectively. Spline yielded the lowest interpolation errors for both steep- and gently-sloping areas with the MAE of 0.010-0.123 and 0.051-0.593 m, respectively when the point density was between 39-77 points/m2. The findings can provide promising potential support to the earth surface process, thereby generating high-resolution DEMs for the topographically complex areas.
LiDAR; DEM; interpolation algorithms; complex topography; Loess Plateau
李朋飞,张晓晨,严露,等. 复杂地形中机载LiDAR点云构建DEM的插值算法对比[J]. 农业工程学报,2021,37(15):146-153.doi:10.11975/j.issn.1002-6819.2021.15.018 http://www.tcsae.org
Li Pengfei, Zhang Xiaochen, Yan Lu, et al. Comparison of interpolation algorithms for DEMs in topographically complex areas using airborne LiDAR point clouds[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(15): 146-153. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2021.15.018 http://www.tcsae.org
2021-03-31
2021-07-07
国家自然科学基金(41807063;41977059)
李朋飞,博士,副教授,研究方向为地貌遥感与土壤侵蚀过程模拟。Email:pengfeili@xust.edu.cn
胡晋飞,博士,讲师,研究方向为水土保持与土壤侵蚀。Email:jinfeih@163.com
10.11975/j.issn.1002-6819.2021.15.018
P237
A
1002-6819(2021)-15-0146-08

