Poisson 3-Lie代数的广义导子

张 爽, 王春月, 张庆成

(1. 吉林建筑大学 基础科学部, 长春 130118； 2. 吉林工程技术师范学院 应用理学院, 长春 130052; 3. 东北师范大学 数学与统计学院, 长春 130024)

1 预备知识

定义1[1]Poisson 3-Lie代数是一个三元组(L,·,[,,]), 其中L是一个线性空间, “·”和“[,,]”分别是L上的双线性映射和三线性映射, 并满足以下条件:

1) (L,·)是交换结合代数；

2) (L,[,,])是3-Lie代数；

3) 对任意的x,y,u,v∈L, [x,y,uv]=u[x,y,v]+[x,y,u]v恒成立.

定义2设(L,·,[,,])是一个Poisson 3-Lie代数,D∈End(L). 若对任意的x,y,z∈L, 均有

D(xy)=D(x)y+xD(y),

(1)

D([x,y,z])=[D(x),y,z]+[x,D(y),z]+[x,y,D(z)]

(2)

成立, 则称D是Poisson 3-Lie代数的导子.

定义3设(L,·,[,,])是一个Poisson 3-Lie代数,D∈End(L). 若存在D′,D″∈End(L), 使得对任意的x,y,z∈L, 均有

D(x)y+xD′(y)=D″(xy),

[D(x),y,z]+[x,D′(y),z]+[x,y,D″(z)]=D‴([x,y,z])

成立, 则称D是Poisson 3-Lie代数的广义导子.

定义4设(L,·,[,,])是一个Poisson 3-Lie代数,D∈End(L). 若存在D′∈End(L), 使得对任意的x,y,z∈L, 均有

D(x)y+xD(y)=D′(xy),

[D(x),y,z]+[x,D(y),z]+[x,y,D(z)]=D′([x,y,z])

成立, 则称D是Poisson 3-Lie代数的拟导子.

记Der(L)为由L所有导子组成的集合, GDer(L)为由L所有广义导子组成的集合, QDer(L)为由L所有拟导子组成的集合.

定义5设(L,·,[,,])是一个Poisson 3-Lie代数,D∈End(L). 若对任意的x,y,z∈L, 式(1)和式(2)均成立, 则称D是Poisson 3-Lie代数的型心. 记C(L)为由L所有型心组成的集合. 若对任意的x,y,z∈L, 均有

xD(y)=D(x)y,

[D(x),y,z]=[x,D(y),z]=[x,y,D(z)]

成立, 则称D是L的拟型心. 由L所有拟型心组成的集合记作QC(L).

定义6设(L,·,[,,])是一个Poisson 3-Lie代数,D∈End(L). 若对任意的x,y,z∈L, 均有

D(xy)=D(x)y=xD(y)=0,

D([x,y,z])=[D(x),y,z]=[x,D(y),z]=[x,y,D(z)]=0

成立, 则称D是Poisson 3-Lie代数的中心导子. 由L所有中心导子组成的集合记作ZDer(L), 称为L的中心导子代数.

定义7设(L,·,[,,])是一个Poisson 3-Lie代数, 称

Z(L)={x∈L|xy=yx=[x,y,z]=[y,x,z]=[y,z,x]=0, ∀y,z∈L}

为L的中心.

由上述定义, 有

ZDer(L)⊆Der(L)⊆QDer(L)⊆GDer(L)⊆End(L),

C(L)⊆QC(L)⊆QDer(L).

通过简单计算可验证End(L)在括积运算[f,g]=fg-gf(∀f,g∈End(L))下是李代数.

2 主要结果

命题1设(L,·,[,,])是一个Poisson 3-Lie代数, 则:

1) GDer(L),QDer(L)和C(L)是李代数End(L)的子代数；

2) ZDer(L)是李代数Der(L)的理想.

证明: 1) 任取D1,D2∈GDer(L), 则对任意的x,y,z∈L, 由广义导子的定义, 有

所以

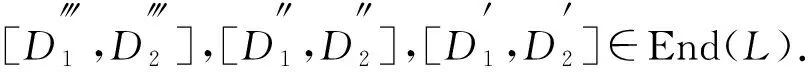
设D1,D2∈C(L), 则对任意的x,y,z∈L, 有

同理可得

[x,[D1,D2](y),z]=[D1,D2]([x,y,z]),

[x,y,[D1,D2](z)]=[D1,D2]([x,y,z]),x([D1,D2](y))=[D1,D2](xy).

所以[D1,D2]∈C(L).因此,C(L)是End(L)的子代数.

2) 任取D1∈ZDer(L),D2∈Der(L), 则对任意的x,y,z∈L, 有

[D1,D2](xy)=D1D2(xy)-D2D1(xy)=D1(D2(x)y+xD2(y))=0,

([D1,D2](x))y=D1D2(x)y-D2D1(x)y=-D2(D1(x)y)-D1(x)D2(y)=0.

所以ZDer(L)是Der(L)的理想.

命题2设(L,·,[,,])是一个Poisson 3-Lie代数, 则：

1) [Der(L),C(L)]⊆C(L)；

2) [QDer(L),QC(L)]⊆QC(L)；

3) [QC(L),QC(L)]⊆QDer(L)；

4) C(L)⊆QDer(L).

证明: 1) 任取D1∈Der(L),D2∈C(L), 则对任意的x,y,z∈L, 有

[D1D2(x),y,z]=D1([D2(x),y,z])-[D2(x),D1(y),z]-[D2(x),y,D1(z)],

从而

[[D1D2-D2D1](x),y,z]=[D1,D2]([x,y,z]),

即

[[D1,D2](x),y,z]=[D1,D2]([x,y,z]).

又因为

(D2D1(x))y=D2D1(xy)-xD2D1(y),

所以([D1,D2](x))y=[D1,D2](xy). 同理可得

[[D1,D2](x),y,z]=[x,[D1,D2](y),z]=[x,y,[D1,D2](z)],

([D1,D2](x))y=x([D1,D2](y)).

因此, [Der(L),C(L)]⊆C(L).

2) 同1)的证明, 经简单计算可得结论.

3) 任取D1,D2∈QC(L), 则对任意的x,y,z∈L, 有

[x,[D1,D2](y),z]=[x,y,[D1,D2](z)]=0,

所以有

[[D1,D2](x),y,z]+[x,[D1,D2](y),z]+[x,y,[D1,D2](z)]=0,

([D1,D2](x))y+x([D1,D2](y))=0.

由拟导子定义得[D1,D2]∈QDer(L). 因此, [QC(L),QC(L)]⊆QDer(L).

4) 任取D∈C(L), 则对任意的x,y,z∈L, 有

[D(x),y,z]=[x,D(y),z]=[x,y,D(z)]=D([x,y,z]),

D(x)y=xD(y)=D(xy).

因此,

[D(x),y,z]+[x,D(y),z]+[x,y,D(z)]=3D([x,y]),

D(x)y+xD(y)=2D(xy).

由D∈End(L)得2D,3D∈End(L), 再由拟导子定义得D∈QDer(L).

定理1设(L,·,[,,])是一个Poisson 3-Lie代数,Z(L)是L的中心, 则

[C(L),QC(L)]⊆End(L,Z(L)).

(3)

特别地, 若Z(L)={0}, 则[C(L),QC(L)]=0.

证明： 任取D1∈C(L),D2∈QC(L), 则对任意的x,y,z∈L, 有

所以[D1,D2](x)∈Z(L), 从而[D1,D2]∈End(L,Z(L)). 因此式(3)成立. 特别地, 若Z(L)={0}, 则[C(L),QC(L)]=Z(L)={0}.

定理2设(L,·,[,,])是一个Poisson 3-Lie代数, 若Z(L)={0}, 则QC(L)是一个李代数当且仅当[QC(L),QC(L)]=0.

证明: 充分性显然, 下证必要性. 任取D1,D2∈QC(L), 对任意的x∈L, 因为QC(L)是一个3-李代数, 所以[D1,D2]∈QC(L), 即

[[D1,D2](x),y,z]=[x,[D1,D2](y),z]=[x,y,[D1,D2](z)],

([D1,D2](x))y=x([D1,D2](y)), ∀y,z∈L.

由命题2中3)的证明, 知

[[D1,D2](x),y,z]=[x,[D1,D2](y)]=[x,y,[D1,D2](z)]=0,

([D1,D2](x))y=-x([D1,D2](y)),

所以有

[[D1,D2](x),y,z]=[y,[D1,D2](x),z]=[x,y,[D1,D2](z)]=0,

([D1,D2](x))y=y([D1,D2](x))=0.

因此[D1,D2](x)∈Z(L)={0}, 即[D1,D2](x)=0. 由x的任意性, [D1,D2]=0, 从而

[QC(L),QC(L)]=0.