测高重力异常中央区奇异积分数值求积公式

宗敬文，李厚朴，纪 兵，欧阳永忠

1. 海军工程大学导航工程教研室，湖北 武汉 430033； 2. 自然资源部海洋环境探测技术与应用重点实验室，广东 广州 510300

海洋重力场数据的获取手段有卫星测高反演、船载及航空重力测量，随着人造地球轨道卫星技术的发展，卫星测高技术促进了大地测量学、地球物理学和海洋学等学科的交叉发展[1]，同时与传统的海洋观测手段相比，能够周期性获取除极地以外的高分辨率、全天候、长时间序列的全球海洋观测数据[2-5]。截至目前，世界上各个国家共计发射测高卫星18颗，其中包括美国海军的Geosat系列、美国宇航局和法国空间研究中心联合发射的T/P系列[6]、欧空局的ERS系列[7]及中国的HY-2A[8]。卫星测高数据遍布全球85°S—85°N的海洋区域，分辨率达1′×1′，精度达1～2 cm，利用高精度、高分辨率卫星测高数据反演重力异常精度已达到10 mGal(1 Gal=10-2m/s2)以内。文献[9]使用逆Stokes法反演中国近海30′×30′海洋重力异常，精度达到3.5 mGal。文献[10]使用Laplace方程的垂线偏差法反演全球海域的重力异常，反演的全球海域1′×1′重力场模型与NGDC船测数据的检核精度达到4～8 mGal。文献[11—14]在卫星测高数据融合和精细处理方面也作出了大量的贡献。

文献[15]利用Stokes公式将卫星测高数据转换为重力异常。文献[16]基于垂线偏差对地形信息敏感的特点，根据边值理论由重力与地形数据确定格网垂线偏差模型。文献[17]提出了利用垂线偏差来反演重力异常的方法，并系统地给出了垂线偏差、扰动重力和重力异常之间的关系表达式，但在利用大地水准面高和垂线偏差反演重力异常实际计算中，计算点及其附近区域到计算点的理论距离近似于零，会导致逆Stokes公式和逆Vening-Meinesz公式中的积分函数产生奇异。文献[18—19]提出一组“非奇异变换”，系统地解决了物理大地测量中高程异常、垂线偏差、地形改正及重力异常梯度等泛函的中央区计算问题。对于中央区积分问题的研究，文献[20—21]将该积分区域视为圆形域，推导的逆Vening-Meinesz公式被广泛应用于反演海洋重力异常。文献[22]在利用逆Vening-Meinesz公式的FFT算法时，考虑了中央区效应的影响，研究表明中央区效应对重力异常的影响可以达到百微伽量级，在高精度重力场计算中是不能忽视的。文献[23—24]分别推导了逆Stokes法和逆Vening-Meinesz法的卫星测高反演重力异常解析计算公式，解决了奇异积分问题，具有较高的计算精度，但解析计算公式系数繁多，计算量大，实际应用中有所不便。因此，为进一步完善卫星测高反演重力异常的计算方法，简化计算过程，提高计算效率，本文采用数值求积公式，分别利用Simpson公式和Cotes公式对逆Stokes法和逆Vening-Meinesz法中的奇异积分问题进行了新的研究，系统地推导出了中央区重力异常的计算公式。此公式可直接利用格网节点处的大地水准面高和垂线偏差计算重力异常值，形式简单，计算效率高，计算精度与解析法计算结果精度相当，可以满足实际应用。

1 逆Stokes公式法奇异积分数值求积公式

由文献[23—24]可知，大地水准面计算重力异常的逆Stokes公式平面近似形式为

(1)

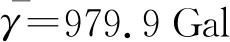
(2)

假设中央区NQ可以展开为如下Taylor级数

NQ=N(x,y)=NP+Nxx+Nyy+

(3)

由式(3)可得

(4)

设中央区积分面积为σ∈[-a≤x≤a,-b≤y≤b]，如图1所示。为方便推导计算，引入新的积分变量u=x/a和v=y/b，因此中央区积分区域面积为σ′∈[-1≤u≤1,-1≤v≤1]。

(5)

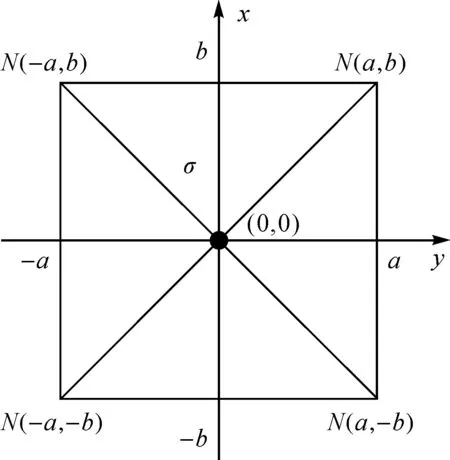
图1 中央区示意图Fig.1 Sketch map of the innermost area

对σ1引入新的积分变量

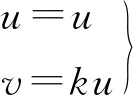
(6)

对σ2引入新的积分变量

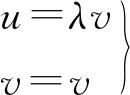
(7)

将式(6)和式(7)代入式(5)，可得中央区IN的表达式为

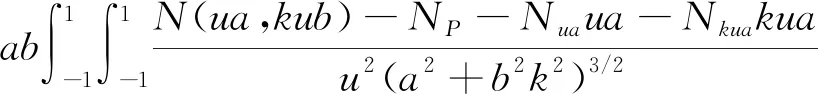
(8)

1.1 基于Simpson公式推导出的逆Stokes公式中央区数值求积公式

利用Simpson公式

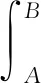
(9)

考虑到式(4)，利用式(9)对式(8)进行u和v方向上数值积分后可得

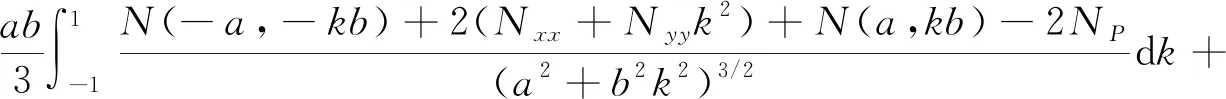
(10)

式中，INS表示基于Simpson公式的逆Stokes法奇异积分数值求积公式。将N(u,v)在u,v=0,±1处的值记为Nij(i,j=0,±1)，并对式(10)在k和λ方向上继续使用Simpson公式，其中

(11)

根据数值微分公式可由节点处大地水准面高求出

(12)

整理后可得

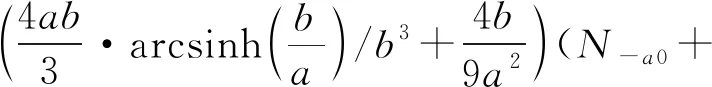
(13)

将式(13)代入式(2)，最后可得中央区重力异常的数值求积公式为

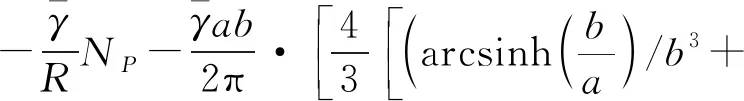
Nab-4NP)

]

(14)

1.2 基于Cotes公式推导出的逆Stokes公式中央区数值求积公式

当只考虑中央区范围为σ∈[-a≤x≤a,-b≤y≤b]时，中央区的影响是不完整的，特别是在起伏变化较大的区域时，考虑将中央区的范围扩大为σ∈[-2a≤x≤2a,-2b≤y≤2b]，因此，本文引入了Cotes公式来计算。推导过程类似于上一部分，首先利用Cotes公式

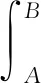
(15)

考虑到式(4)，利用式(15)对式(8)进行u和v方向上数值积分后可得

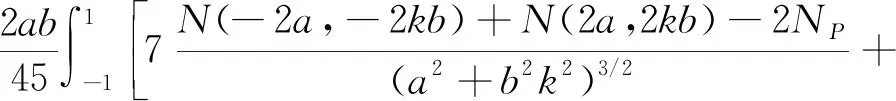
(16)

式中，INC表示基于Cotes公式的逆Stokes法奇异积分求积公式。

如图2所示，将N(u,v)在u,v=0,±1,±2处的值记为Nij(i,j=0,±1,±2)，对式(16)在k和λ方向上继续使用Cotes公式，并考虑到式(11)和式(12)，整理后可得

Na-2b+N-a2b+N-a-2b-8NP)

}

(17)

将式(17)代入式(2)中，最后可得中央区重力异常的数值求积公式为

N-2a-2b+N-2a2b+N2a-2b-4NP)+

N-2a-b+Na2b+Na-2b+N-a2b+

N-a-2b-8NP)

}

(18)

图2 Cotes公式中央区示意图Fig.2 Sketch map of the innermost area used the Cotes formula

利用式(14)和式(18)计算中央区重力异常时，可直接使用已知网格节点处的大地水准面高作为输入值，相较于利用解析法的求解过程减少了求解多项式系数的步骤，大大简化了逆Stokes法反演重力异常的过程，从而提高了计算效率。

2 逆Vening-Meinesz公式法奇异积分数值求积公式

由文献[25—26]可知，垂线偏差计算重力异常的逆Vening-Meinesz公式平面近似形式为

(19)

式中，ξQ、ηQ为移动点处的垂线偏差；ξP、ηP为计算点处的垂线偏差。为便于计算，令

(20)

将垂线偏差ξQ、ηQ在中央区展成如下Taylor级数

(21)

由式(21)得出

(22)

由于积分区域的对称性，并考虑到式(6)和式(7)，式(20)可改写为

(23)

2.1 基于Simpson公式推导出的逆Vening-Meinesz公式中央区数值求积公式

利用式(9)，并考虑到式(22)，对式(23)中积分部分进行u和v方向上数值积分后可得

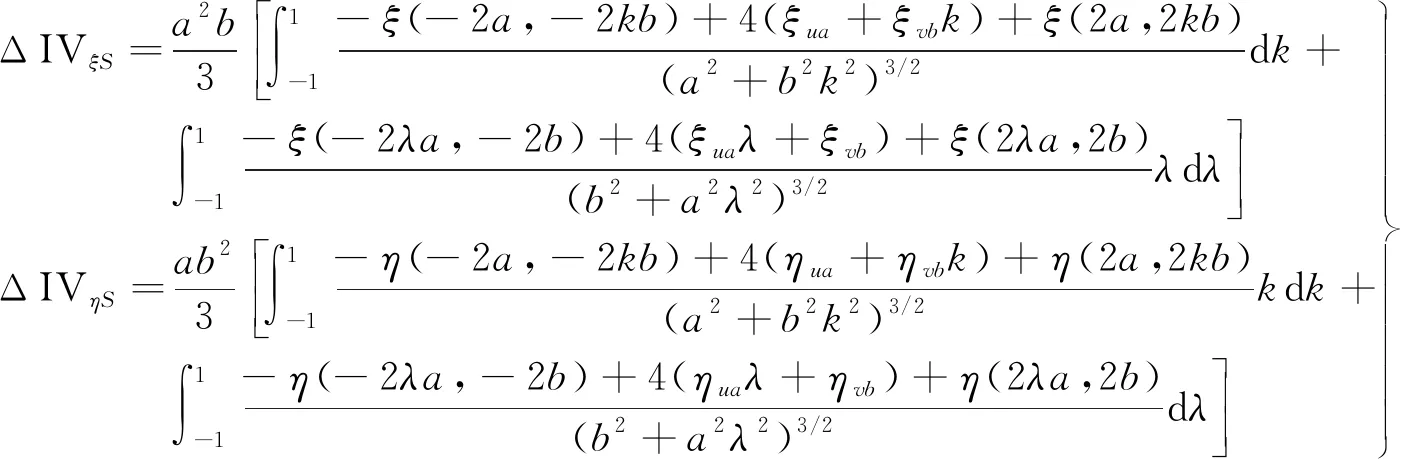
(24)

将ξ(u,v)、η(u,v)在u、v=0、±1处的值记为ξij、ηij(i,j=0、±1)，并考虑到根据数值微分公式可由节点处垂线偏差求出

(25)

最后对式(24)在k和λ方向上继续使用Simpson公式，整理后得

(26)

式中，ΔgξS、ΔgηS表示基于Simpson公式的逆Vening-Meinesz法奇异积分数值求积公式。因此，式(26)即为基于Simpson公式的逆Vening-Meinesz法反演中央区重力异常的数值求积公式。

2.2 基于Cotes公式推导出的逆Vening-Meinesz公式中央区数值求积公式

同样，当只考虑中央区范围为σ∈[-a≤x≤a,-b≤y≤b]时，中央区的影响是不完整的，特别是在起伏变化较大的区域时，考虑将中央区的范围扩大为σ∈[-2a≤x≤2a,-2b≤y≤2b]，因此，本文引入了Cotes公式来计算。利用式(15)并考虑到式(22)，对式(23)中积分部分进行u和v方向上数值积分后可得

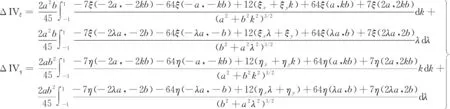
(27)

如图2所示，将ξ(u,v)、η(u,v)在u,v=0,±1,±2处的值记为ξij、ηij(i,j=0,±1,±2)。对式(27)在k和λ方向上继续使用Cotes公式，并考虑到式(11)和式(25)，整理后可得

(28)

式中，ΔgξC、ΔgηC表示基于Cotes公式的逆Vening-Meinesz法奇异积分数值求积公式，因此，式(28)即为基于Cotes公式的逆Vening-Meinesz法反演中央区重力异常数值求积公式。利用式(26)和式(28)计算中央区重力异常时，可直接使用已知网格节点处的垂线偏差作为输入值，相较于利用解析法的求解过程减少了求解插值多项式系数的步骤，从而简化了逆Vening-Meinesz公式反演重力异常的计算过程，提高了计算效率。

3 算例分析

3.1 理论模型检验

为验证本文推导的基于数值求积公式的测高反演重力异常普适计算公式的准确性和可靠性，假定大地水准面高和垂线偏差为理论模型值，计算了非奇异变换前、后求积公式计算结果，分析比较了非奇异变换后两种不同普适数值求积公式的计算精度。现设计如下两个算例。

3.1.1 理论模型1

取中央区大地水准面高的数学模型为

(29)

中央区垂线偏差的数学模型为

(30)

根据本文推导出的普适数值求积公式取a=1,b=1，因此中央区范围为σ∈[-2≤x≤2,-2≤y≤2]，δ为平滑因子，则NP=NQ(0,0)=δ，ξP=ξQ(0,0)=0，ηP=ηQ(0,0)=0。以δ取10时为例，大地水准面高如图3所示。

图3 大地水准面高Fig.3 Geoidal height

(31)

为验证非奇异变换前、后积分表达式精度，分别取δ=1、5、10时，IN1和IN2在不同等分区间下的计算结果列于表1。

由表1可知，非奇异变换后IN250×50等分计算结果的准确度和非奇异变换前IN1500×500等分计算结果的准确度基本相同。由图4(a)可以看出，非奇异变换前在低等分区间精度较低且收敛速度慢，非奇异变换后的收敛速度要大于变换前且计算结果更接近真值。因此，非奇异变换后的积分公式计算效率更高，收敛速度更快且精度更高。为进一步分析比较基于Simpson公式和Cotes公式的逆Stokes法反演中央区重力异常普适数值计算公式，利用大地水准面高理论模型1，取IN24000×4000等分的计算结果为准确值，式(13)和式(17)的计算结果分别记为INS和INC，将δ分别取δ=3,5,8,10时的计算结果列于表2。

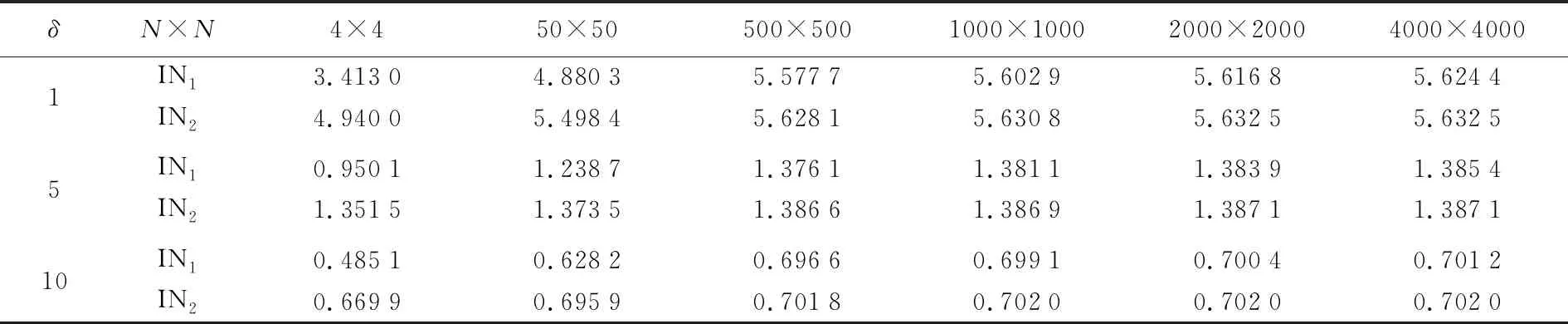
表1 非奇异变换前后奇异积分计算结果

图4 δ=10时非奇异变换前后不同等分区间积分数值Fig.4 Results of singular integral before and after the non-singular transformation

由表2可知，当δ=3，5时，Cotes公式法的相对误差小于Simpson公式法；当δ=8，10时Simpson公式法的相对误差要小于Cotes公式法。Simpson公式法数值计算公式的相对误差波动较大，与平滑因子δ取值有关，大地水准面高变化缓和地区相对误差较小，精度较高；Cotes公式法数值计算公式的相对误差比较稳定，随着平滑因子δ取值变化，精度受影响较小，但精度稍低。相比较于Cotes公式法，Simpson公式法在平缓地区具有更好的计算精度，但其计算精度波动较大；相比较于Simpson公式法，Cotes公式法具有更好的计算稳定性，计算精度受地形影响较小。

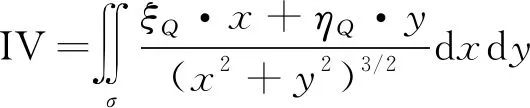
(32)

为验证非奇异变换前、后积分表达式精度，分别取δ=1、5、10，IV1和IV2在不同等分区间下的计算结果列于表3。

表2 非奇异变换后数值解计算结果误差

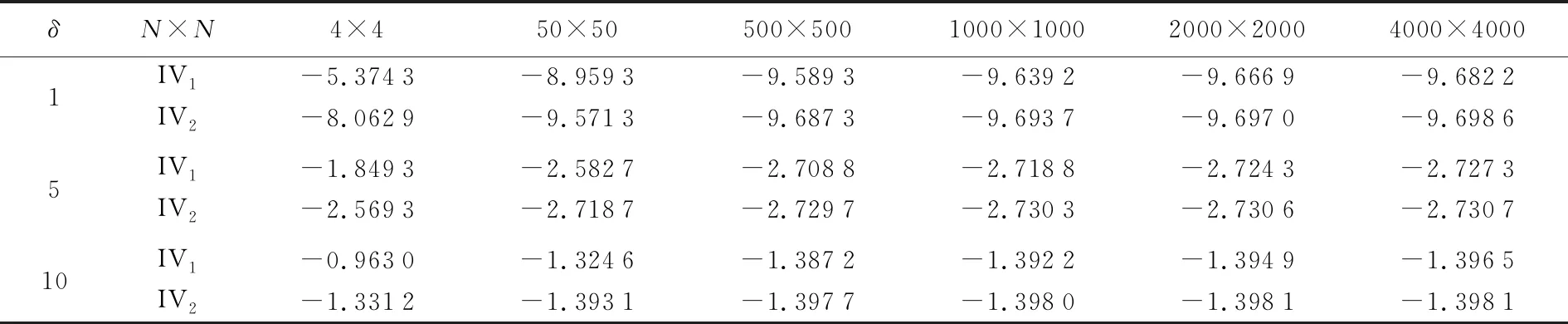
表3 非奇异变换前后奇异积分计算结果

表4 非奇异变换后数值解计算结果误差

由表4可知，Cotes公式法数值计算公式的相对误差明显小于Simpson公式法数值计算公式，Simpson公式法数值计算公式的相对误差波动较大，与平滑因子δ取值有关；Cotes公式法数值计算公式的相对误差比较稳定，当δ分别取δ=3,6,8,10时，相对误差均小于1%，相比较于Simpson公式法数值计算公式，Cotes公式法数值计算公式具有较好的计算精度和稳定性。

文献[23]和文献[24]分别推导了双二次多项式插值表示下的大地水准面高和垂线偏差非奇异积分解析计算公式。记录其结果分别为IN3和IV3

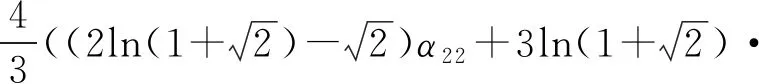
(α02+α20))

(33)

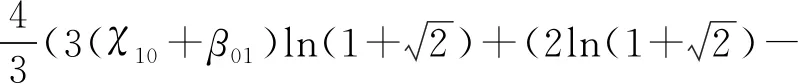
(34)

式中,IN3为双二次多项式插值表示下的大地水准面高非奇异积分解析表达式；IV3为双二次多项式插值表示下的垂线偏差非奇异积分解析表达式。以非奇异变换后4000×4000等分区间计算结果作为准确值，其中逆Stokes法准确值记为IN2，逆Vening-Meinesz法准确值记为IV2，式(13)、式(17)、式(26)和式(28)的计算结果分别为INS、INC、IVS和IVC，计算结果及其相应计算误差见表5。

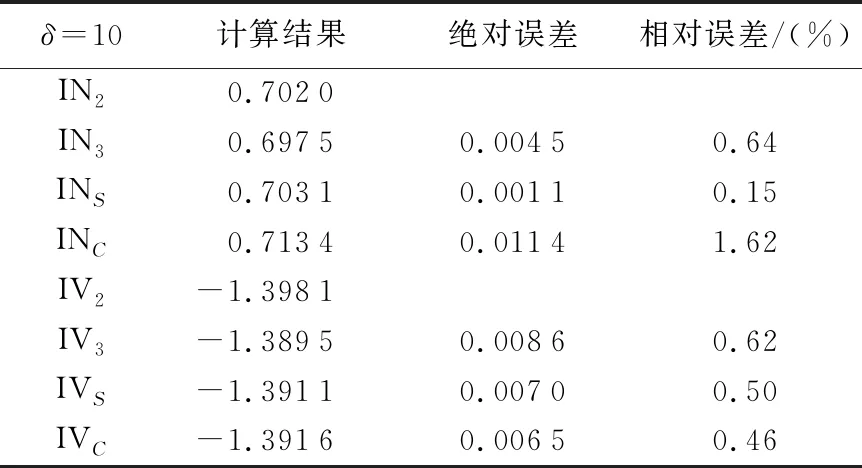
表5 非奇异变换后解析解与数值解的计算误差

分析表5可知，逆Stokes法重力异常求积公式解析解与准确值的相对误差为0.64%，Simpson公式数值解与准确值的相对误差为0.15%，Simpson公式数值解精度高于解析解计算精度，二者相对误差均小于1%，而Cotes公式数值解计算精度较低，相对误差为1.62%；逆Vening-Meinesz法重力异常求积公式解析解与准确值的相对误差为0.62%，Cotes公式数值解与准确值的相对误差为0.46%，Simpson公式数值解与准确值的相对误差为0.50%，解析解计算精度略低于数值解计算精度，三者相对误差均小于1%。

3.1.2 理论模型2

在理论模型1的分析基础上，理论模型2仅用于分析两种不同数值积分方法下测高反演重力异常普适计算公式的准确性和可靠性。取中央区大地水准面高的数学模型为

(35)

中央区垂线偏差的数学模型为

(36)

现取a=1,b=0.7，因此中央区范围为σ∈[-2≤x≤2,-1.4≤y≤1.4]，δ为平滑因子，则NP=NQ(0,0)=δ，ξP=ξQ(0,0)=0，ηP=ηQ(0,0)=0。以δ取10时为例，大地水准面高如图5所示。

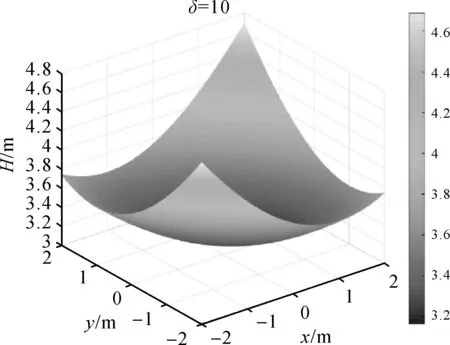
图5 大地水准面高Fig.5 Geoid height

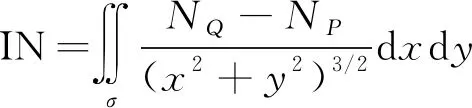
(37)

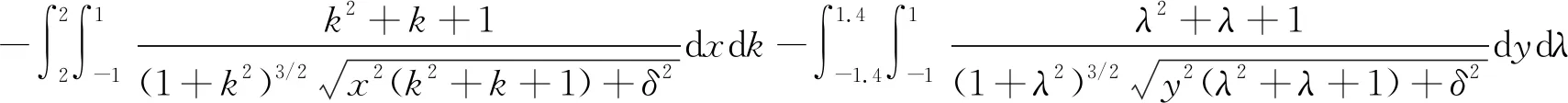
(38)

为分析比较基于Simpson公式法和Cotes公式法的逆Stokes法反演中央区重力异常普适数值计算公式，利用大地水准面高理论模型2，式(13)和式(17)的计算结果分别记为INS和INC，将δ分别取δ=3，5，8，10时的计算结果列于表6。

表6 非奇异变换后数值解计算结果误差

由表6可知，当δ=3时，Cotes公式法的相对误差小于Simpson公式法；当δ=5、8、10时，Simpson公式法的相对误差小于Cotes公式法。Simpson公式法数值计算公式的相对误差波动较大，当平滑因子变大时，计算精度较高，相对误差小于0.5%；Cotes公式法数值计算公式的相对误差比较稳定，随着平滑因子δ取值变化，精度受影响较小，但精度稍低。相比较于Cotes公式法，Simpson公式法在平缓地区具有更好的计算精度，但其计算精度波动较大；相比较于Simpson公式法，Cotes公式法具有更好的计算稳定性，计算精度受地形影响较小。

利用垂线偏差理论模型2，式(26)和式(28)的计算结果分别为IVS和IVC，将δ分别取δ=3,5,8,10时的计算结果列于表7。

表7 非奇异变换后数值解计算结果误差

由表7可知，Cotes公式法数值计算公式的相对误差比较稳定，当δ分别取δ=3,5,8,10时，计算结果的相对误差均小于0.5%；Simpson公式法数值计算公式的相对误差波动较大，且当δ=3,5时，相对误差较大，当δ=8,10时，相对误差小于0.5%。对比发现，Cotes公式法数值计算公式相比较于Simpson公式法数值计算公式具有较好的计算精度和计算稳定性。

将式(33)和式(34)中解析解计算结果与本文推导公式进行比较，取δ=10时，以式(37)、式(38)非奇异变换后4000×4000等分区间计算结果作为准确值，其中逆Stokes法准确值记为IN22，逆Vening-Meinesz法准确值记为IV22，IN3、INS、INC、IV3、IVS和IVC计算结果及其相应计算误差见表8。

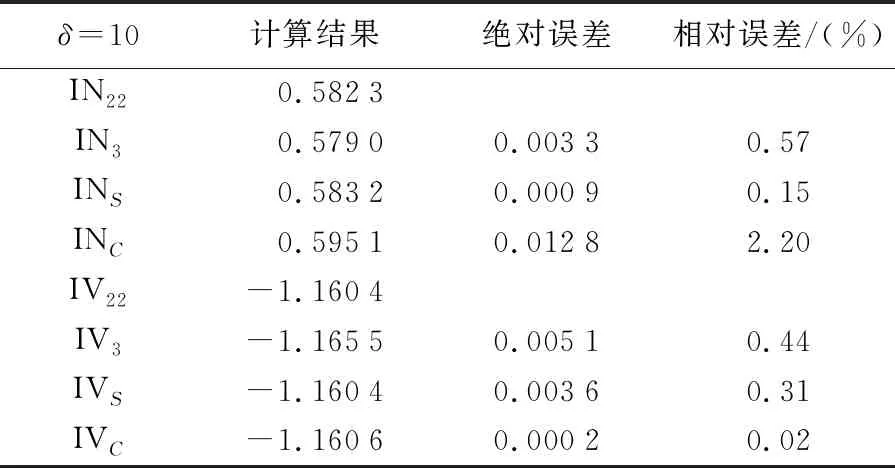
表8 非奇异变换后解析解与数值解的计算误差

分析表8可知，其中逆Stokes法重力异常数值求积公式解析解与准确值的相对误差为0.57%，Simpson公式法数值解与准确值的相对误差为0.15%，Simpson公式法数值解精度高于解析解计算精度，二者相对误差均小于0.6%，而Cotes公式数值解计算精度较低，相对误差为2.20%；逆Vening-Meinesz法重力异常数值求积公式解析解与准确值的相对误差为0.44%，Cotes公式法数值解与准确值的相对误差为0.02%，Simpson公式法数值解与准确值的相对误差为0.31%，数值解计算精度略高于解析解计算精度。

本文通过利用两种不同理论模型，分析比较基于Simpson公式法和Cotes公式法两种不同数值求积方法推导出的测高反演重力异常普适计算公式，发现在逆Stokes法重力异常求积公式计算中，Simpson公式法计算精度较好，但受地形影响其误差波动较大，适用于中央区变化比较平缓地区，Cotes公式法计算误差稳定性较高，但计算精度略低；在逆Vening-Meinesz法重力异常求积公式中，Cotes公式法计算精度和计算误差稳定性都优于Simpson公式法，且计算精度优于解析法计算精度，可以满足应用要求。

3.2 试验数据检验

理论模型下的精度检验表明，本文推导出的中央区奇异积分数值求积公式有较高的计算精度且形式简单。为进一步说明中央区奇异积分数值求积公式的计算精度及中央区对重力异常的影响，选定南海16°N-20°N，112°E-116°E海域作为计算区域，以EGM2008地球重力场模型计算得到的2′×2′分辨率的大地水准面高数据作为试验数据，计算海域大地水准面高分布图如图6所示，计算海域共记119×119个格网，中央区为8′×8′(4×4个格网)，采用逆Stokes法利用式(33)、式(14)和式(18)实际计算了该区域的中央区重力异常，结果分别记为Δg1、Δg2、Δg3列于表9，计算结果之间的比较情况见表10。

由表9和表10可以看出，3种计算方法计算出的4×4个格网大小的中央区重力异常平均值分别为-1.088、-1.089、-1.087 mGal，三者差异较小；标准差分别为2.60、2.63、2.83 mGal；Simpson公式法与解析法计算得到的中央区重力异常差值的标准差为0.030 mGal，最大值为0.195 mGal，最小值为-0.129 mGal,因此当考虑中央区范围扩大为4×4个格网时，Simpson公式法和解析法计算结果相当；Cotes公式法计算出的重力异常最大值为14.39 mGal，最小值为-13.23 mGal，与Simpson公式法和解析法计算得到的中央区重力异常差值的标准差分别为0.533 mGal和0.545 mGal，最大值分别为3.806 mGal和4.254 mGal，最小值分别为-4.167 mGal和-3.879 mGal,Cotes公式法与另外两种方法计算结果具有一定差距，这是由于Cotes公式法计算过程中计算点更多，反映出利用该方法计算中央区重力异常变化更为明显,可以更好地反映出起伏较大区域中央区重力异常变化。同时，试验数据说明，分别利用3种不同方法计算出的4×4个格网中央区重力异常范围为-13.5 mGal～+14.5 mGal，因此在高精度重力异常反演时，中央区有不容忽视的贡献。

图6 计算海域大地水准面高示意图Fig.6 Sketch map of geoidal height in the caculating sea area

表9 逆Stokes法反演中央区重力异常统计情况

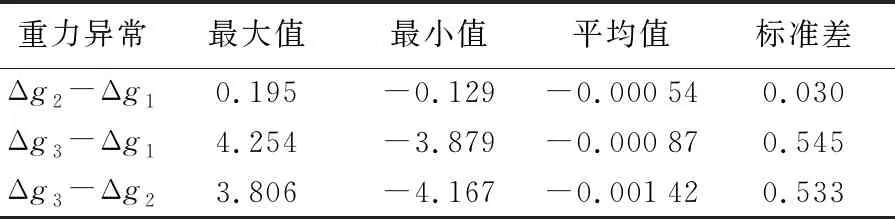
表10 3种方法计算结果比较

4 结 论

为完善卫星测高反演重力异常的计算理论，本文利用Simpson公式和Cotes公式的数值求积方法，系统地推导出了逆Stokes法和逆Vening-Meinesz法反演中央区重力异常普适数值积分公式，利用理论模型和试验数据进行了分析检验。研究表明：

(1) 非奇异变换后公式的计算效率要高于非奇异变换前，且计算精度更高。

(2) 通过将逆Stokes法和逆Vening-Meinesz法奇异积分解析法计算结果与数值计算结果相比较，发现数值法计算结果精度优于解析法计算结果，相对误差均小于1%，完全可以满足实际应用。

(3) 本文推导出的普适数值求积公式可以直接利用网格节点处的大地水准面高和垂线偏差计算重力异常，形式简单，避免了传统解析表达式系数繁多、形式复杂的缺点，在确保了公式计算精度的同时也提高了计算效率。

(4) 试验数据下的分析表明，在利用逆Stokes法反演重力异常时，解析法与数值法计算结果相当，且中央区有不容忽视的贡献。