基于直线电动机的3-PSS并联机器人机构设计与仿真分析

朱祺珩，尹凝霞，魏远鹏，黄恒威，王翔宇

（广东海洋大学 机械与动力工程学院，广东 湛江 524088）

0 引言

机器人作为一种新兴的可从事多种繁琐重复或危险工作的自动化设备，不仅减轻了人类的工作强度，而且提高了产品的生产效率和产品精度[1]。为缩短产品生产周期，串联机器人率先被投入到全自动化的生产流水线[2]。但随着经济的快速发展，串联机器人已无法满足电子、液晶等小件产品的自动化生产需求，于是并联机器人应运而生[3]。并联机器人高精度、高速度且无须较大工作空间等特点使其在实际生产中得到了广泛应用，因此并联机器人也成为机器人研究中一个热门的方向[4]。

澳大利亚的Hunt创造性地提出将Stewart机构作为机器人操作器，并提出了3PRS机构，该机构实现了动静平台在平行和非平行两种情况下的两转一移[5]。20世纪90年代后期，伺服技术和工业PC的出现促进了并联机器人的发展。并联机器人因结构稳定、承载能力强、累积误差小和响应速度快等优点广泛用于并联机床、航空航天、医学精密仪器等[6]。1998年，Clavel第一次提出了纯平移的三自由度并联机器人，主要由动、静平台组成，静平台上面安装电动机，使运动部件的质量降低，提高了执行末端的速度[7]。因此，三自由度机器人成为新的研究热点。在三自由度并联机器人研究进程中，李剑峰[8]分析了3RPS、3RRS等三平移并联机构的运动学和动力学问题；郝亮亮等[9]开展了3-PRS并联机构的逆运动学分析，并进行了连杆形成限制条件及球面副和转动副转交约束条件的机构空间预估。2011年意大利的Fabrizio Patane[10]针对一种主动杆分别沿等边三角形的三边移动的3-PSS并联机构进行了仿真研究。但三自由度并联结构还存在不足，如并联机构的冗余约束和复合驱动、运动空间小，以及大部分并联机器仍然采用旋转电动机而限制其运动速度的问题。

本研究利用SolidWorks设计出一种以直线电动机为驱动，定平台、动平台及3条支链对称分布的3-PSS并联机器人结构。直线电动机可直接将电能转化为直线运动机械能，省去中间转化机构传动装置且易于控制，响应速度更快；同时3条支链对称分布，使其有更好的同向性，有利于机器人整体性的轨迹规划。

1 3-PSS简化模型建立

本文研究的并联机器人的结构由固定不动的静平台、3块相同的连接板、3个相同的平行四边形运动支链和动平台组成。运动支链由4个球铰对称连接，运动支链与动平台和连接板与电动机动子均为螺栓连接。直线电动机均匀安装在静平台上，每个连接板与直线电动机动子固连，均由直线电动机动子移动副驱动，3个平行四边形闭环机构使动平台在移动过程中始终保持平行，消除动平台的旋转。机器人简化模型如图1所示。

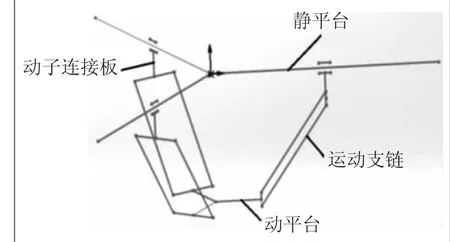
图1 3-PSS并联机器人简化模型

2 3-PSS并联机器人自由度计算

并联机构的自由度指在满足工作要求的条件下末端执行器具有确定的相对运动所需要的最少独立自由度数，一般由运动副的数目类型、运动支链及构件数的相互约束条件决定。对于刚体空间自由度而言，由Grubler-Kutzbach自由度计算公式得

3 并联机器人运动学分析

3.1 运动学反解

图2 Hi（i=1,2,3）计算示意图

图3 Di（i=1,2,3）计算示意图

其中，设置O′在静坐标系下的坐标为（x, y, z）,矢量T表示以静平台中心O为起点，动平台中心O′为终点的向量,T=[x y z]T；将各支链杆向量HiDi记为Li。

基于向量点乘原则，又由式（4）可得

图4 3-PSS平动并联机器人坐标系图

3.2 运动学正解

式中：r1=r2=r3；l1=l2=l3。

由式（13）可知，运动学正解存在多组解和解析解，这使得对所设计的3-PSS并联机器人的控制变得相对简单，这也是本设计的优点所在。当x、y、z都取正值时，直线导轨滑块和动平台满足坐标系方向。

4 逆动力学建模求解

对上文已经建立的3-PSS物理模型进一步分析，假设三自由度并联机器人第i个滑块上受到的驱动力为FHi，方向沿着滑块运动的方向；滑块受到静平台对它的反力为Ffi；动平台质心受到的阻力为FD，由于所设计的三自由度并联机器人始终保持平动运动状态，则其所受阻力矩为0；第i个导轨滑块对第i个支链的作用力为FHiLi；第i个支链对动平台的作用力为FLi。Jcj为各支链杆对其质心惯性张量；Jd为动平台质心的惯性张量。假设mHi为第i个导轨滑块的质量；mi为第i个支链连杆质量；md为动平台质量，其中i=1,2,3,对滑块、动平台、支链连杆建立牛顿方程可得以下几个方程：

式中：ωj为支链杆的角速度矢量，可由上文运动学分析得出；lcihi为质心Ci指向滑块球铰的矢量；ldi为动平台质心指向动平台球铰的矢量。

由于动平台始终进行平移运动，则其动平台质心力矩为0。对上面各式进行联立求解，则在已知动平台质心所受阻力FD情况下可求出FHiLi、FLi。

5 Adams仿真分析

5.1 虚拟样机模型建立

使用SolidWorks 软件建立并联机器人实体三维模型，取杆的初始长度为550 mm，导轨长度为700 mm。将装配体导入软件中显示如图5所示。

图5 虚拟样机实体模型

通过ADAMS软件中自带的模型验证功能，对所建立的模型的自由度数、运动副数目、构件的数目，以及是否存在过约束进行验证，所建立的样机模型验证正确。

5.2 轨迹规划

本文设计的三自由度并联机器人拟用于糕点包装搬运的场合，并基于糕点的生产参数进行轨迹规划设计。糕点质量为55～60 g，糕点尺寸约为100 mm×60 mm×20 mm，为方便计算，设置糕点与包装盒中心距离为320 mm，在初始位置向下运动夹取糕点的距离为80 mm，1个盒子可装2个糕点，另一方向中心距离为80 mm，考虑实际作业要求，对中间轨迹采用圆角矩形路径，避免拐角点出现冲击和振荡。其返回路程无须与初始行程轨迹完全重合，允许拐角不重合，路径如图6所示。

图6 运动路径

假设这一过程消耗的时间为T=1 s。在ADAMS软件中的XOZ平面进行仿真。设置仿真时间为1 s，步数设置200步，选择上文所设置的Marker点(动平台质心)为末端执行器执行的关键点，对其添加三维驱动。采用STEP函数，计算各部分路径所消耗的时间。为了确定所设置的函数是否符合预期的运动轨迹曲线，进行验证操作。末端执行器按照预定轨迹做门字形运动，基本满足轨迹要求，如图7所示。

图7 末端执行器仿真轨迹

调用其绘图工具，首先将source改为Object,将Filter设置为Constraint,然后在Object选取动平台，在characteristic（特性）中分别选取速度、加速度和位移，独立轴选用时间，如图8～图11所示。

由图8、图9可知，末端执行器在x方向高速运动时，在0.10～0.15 s、0.35～0.40 s、0.60～0.65 s、0.85～0.90 s时间段并联机器人停止x方向运动，与所设计轨迹函数相对应，末端向下移动、夹取并上升往回走；由z方向速度曲线，其在0.075 s运动，与x方向0.750～0.100 s、0.150～0.175 s、0.325～0.350 s、0.400～0.425 s、0.575～0.600 s、0.650～0.675 s、0.825～0.850 s、0.900～0.925 s时间段共同产生圆弧运动，与上文运动轨迹曲线一致；同时y向曲线初值为0，至T=0.75 s开始向y方向运动。图9曲线光滑表示末端执行器在高速运动场合运行平稳。

图8 末端执行器各方向速度变化曲线

图9 末端执行器合速度变化曲线

由图10可知，动平台加速度曲线比较陡，过渡不平缓，对电动机性能要求较高，但其最大加速度未超过电动机允许的最大加速度，能满足工作要求。由图11可知，末端执行器可按照设计轨迹运行，杆件长度、导轨长度及球铰转动角度均满足工作空间要求，其中动平台x方向移动位移为±160 mm，z方向移动位移为±80 mm，Y方向移动位移为±80 mm，符合函数设计预期结果，位移曲线光滑无突变，运动性能较好。

图10 末端执行器加速度变化曲线

图11 末端执行器位移变化曲线图

5.3 运动学反解仿真

由于ADAMS软件中起始坐标原点与三自由度并联机器人静平台的中心并不重合，再根据实际装配中球铰大小及滑块连接板的长度，出于计算方便，设置栅格间隔为10 mm，以滑块2为研究对象，采取运动轨迹中的几点进行运动学的验证，用MATLAB软件辅助计算。分别代入坐标值输入各参数，再在ADAMS软件中获取对应各坐标值所对应的滑块2的数值。各对应值如表1所示。

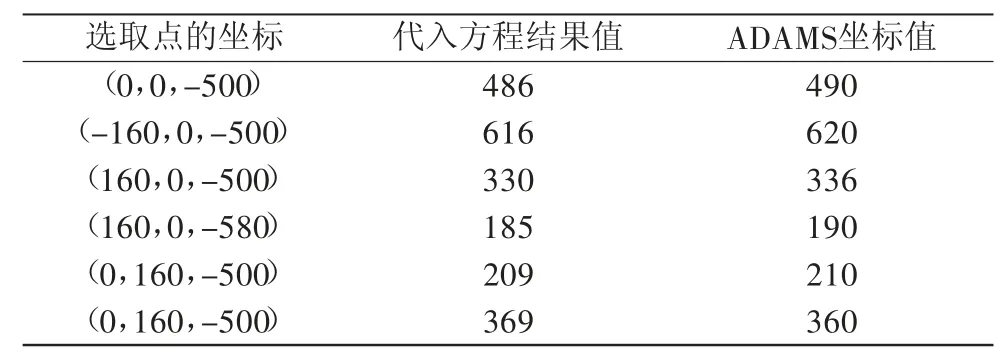
表1 各路径点对应的滑块2的运动学逆解方程值和坐标值

所设置栅格间隔为10 mm，对比所选取点在运动学反解方程结果值与在软件中获取的坐标值，其中两者的值大小相同，即可验证运动学反解方程结论正确。

5.4 运动学正解仿真

在ADAMS中对导轨滑块设置移动副驱动，给定3个滑块移动副的位移函数，可绘制曲线观察函数的运行规律，进而测量动平台末端点的速度、加速度及位移等曲线，探讨其运动规律。由于并联机器人运动学正解比较复杂，故没有运用正解方程，而是通过选取在其工作空间内的驱动函数，如下所示：

设置仿真时间t=3 s，步数为600，其各关系曲线如图12所示。

图12 3个滑块位移变化曲线

5.5 动力学仿真

设置各零件材料为铝合金，其动平台的初始质量测得为1.2 kg，修改其质量，模拟仿真在不同的质量下滑块驱动力的变化规律。为方便研究，采用上文中3个滑块的驱动函数。

以滑块1为研究对象，其在动平台不同质量的状态下滑块的驱动力、速度变化曲线分别如图13、图14所示。由图13和图14分析可得，滑块所受的驱动力随着动平台质量的增加而增大，当质量呈比例增加时，驱动力也呈比例增加；当驱动函数为正余弦驱动时，滑块速度平稳无突变。在滑块速度保持不变的条件下，当所夹取的物体越重，为维持运动状态不变，所需要的力越大，电动机所消耗的能量越多，对电动机要求也越高。通过此方式研究并联机器人夹取质量的极限，再借助实验验证，可以避免过载情况，保护并联机器人。

图13 不同质量下滑块驱动力的变化曲线

图14 不同质量下滑块速度的变化曲线

为进一步探究动平台材料不同对驱动力的影响，采用3种常见的材料进行虚拟仿真，分别是碳纤维、铝合金和钢铁，如图15所示。由图15分析可知，当材料为钢铁时，滑块所受驱动力明显高于碳纤维和铝合金。而铝合金又稍高于碳纤维，故不宜采用钢铁为三自由度并联机器人的材料，可根据经济成本适当选用碳纤维和铝合金两种材料。

图15 不同材料下滑块驱动力的变化曲线

6 结语

1）利用SolidWorks对3-PSS并联机器人建立简化模型，计算其自由度，建立其约束方程对运动学进行分析，得出运动学位移逆解与正解模型。

2）分析其各部件受力情况，对其进行了逆动力学分析。

3）对所建立模型自由度进行验算，对其进行运动轨迹的规划及运动学和动力学仿真分析。