重载无人机弧齿锥齿轮动力学分析

马源辰，郑鹏

（沈阳工业大学 机械工程学院，沈阳 110870）

0 引言

随着科学技术的发展，无人机已成为商业、军事、制造业不可或缺的一部分[1]。目前，在重载无人机的研究领域中，旋翼式无人机逐渐成为研究热点。与传统无翼式重载无人机相比，旋翼式无人机能够以任意角度和方向起飞、降落、悬停[2]，具有极强的环境适应能力。同时还具备极大的承载能力，这主要得益于负责旋翼转动的弧齿锥齿轮减速器。

弧齿锥齿轮作为重载旋翼无人机的核心传动部件，具有极高的传动、承载能力。但由于其齿面结构复杂[3]，对工作环境的影响较为敏感，在恶劣的情况下可能导致齿轮轮齿折断、疲劳破坏。本文通过分析重载无人机在不同工况下其内部弧齿锥齿轮的动力学特性，进而制定无人机的工作条件，保证齿轮在合理的工作条件下运转。

1 弧齿锥齿轮动态特性分析

在一对轮齿啮入的瞬间，由于受到瞬时载荷发生弹性变形, 齿轮在啮合点处的瞬态法向相对速度产生差异从而引起啮合冲击[4]，影响齿轮传动的平稳性。同时，由于工作环境导致齿轮负载转矩瞬间增大从而产生瞬时冲击载荷，为了提高齿轮系统的平稳性，利用UG动力学分析模块研究弧齿锥齿轮在不同工况下的动态特性。

1.1 冲击函数模型建立

本文使用UG中的Adams求解器进行求解，使用自带的Impact函数来计算接触力[5]，该函数基于Hertz弹性碰撞理论，能够准确地反映齿轮传动时的输入和输出情况，公式如下：

式中：l为接触时的距离；l1为接触前的距离；e为接触碰撞指数；Cmax为最大阻尼系数；d为全阻尼状态的边界穿透量；k为刚度系数，其计算公式为

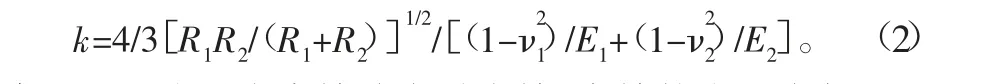
式中：R1、R2分别为齿轮啮合时小轮、大轮的当量半径；E1、E2分别为小轮、大轮的弹性模量；ν1、ν2分别为小轮、大轮材料的泊松比。

1.2 变转速工况下齿轮动态特性分析

结合重载无人机的使用工况，设定其转速为3000 r/min（18 000（°）/s），为避免传动开始由于冲击导致转速突变，设置主动小轮的转速函数为从0 s开始的线性函数，同时，为探究不同转速下对齿轮啮入冲击的影响，将速度设计为3个阶段（即1000、2000、3000 r/min）,最终定义转速函数为STEP(time,0,0d,0.05,6000d)+STEP(time,0.1,0d,0.15,6000d)+STEP (time,0.2,0d,0.25,6000d)，在大轮上设置恒定负载为-100 N·mm。齿轮材料为渗碳钢，弹性模量E1=E2=2.0675×105MPa，泊松比ν1=ν2=0.3。将上述参数代入公式，得到刚度系数k=6.73×105N·mm；接触碰撞指数e取值为1.5；最大阻尼系数Cmax取值为45 N·mm；嵌入深度取0.1 mm；动摩擦因数、静摩擦因数分别取0.06和0.08。设置参数后，导入UG进行动力学仿真。取分析时间为0.3 s，分析步长为5000。

主动小轮输出角速度随时间变化如图1所示，主动轮转速分别在0.05、0.15、0.25 s处达到平衡，由于小轮未施加负载，因此在平衡处的转速值分别为6000、12 000、18 000（°）/s，符合给定速度函数的规律。

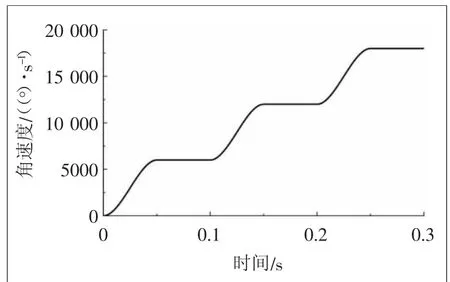
图1 主动小齿轮角速度变化曲线

被动大轮理论输出角速度随时间变化，如图2所示。由于齿轮在传动过程中发生单双齿交替啮合，齿轮的啮合刚度发生周期性变化，在每一次啮合的开始和结束阶段均产生碰撞冲击[6]，因此大轮的转速在理论值附近发生周期性波动。当转速的理论值分别达到6000、12 000、18 000（°）/s时，齿轮实际转速的平均值为5999.97、12 000.06、17 999.97（°）/s。误差值极小，符合齿轮的使用要求。但是随着转速的增加，其上下波动幅度、频率随之增大，齿轮啮合冲击影响也逐渐增大，可能会引起齿轮的疲劳破坏和寿命减少，因此在运行过程中尽量避免过高速运动。

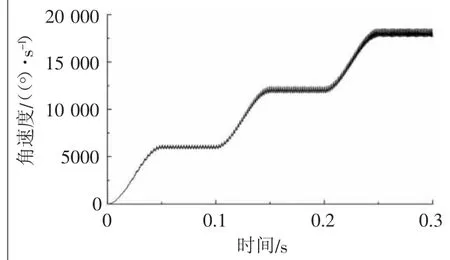
图2 被动大齿轮角速度变化曲线

图3为恒负载、变转速条件下齿轮啮合力随时间的变化曲线，由于受恒定负载影响，齿轮在开始啮合时发生冲击导致啮合力突增，然后回归至正常范围，之后不断增大幅度，啮合力分别在附近波动，符合弧齿锥齿轮的啮合规律。

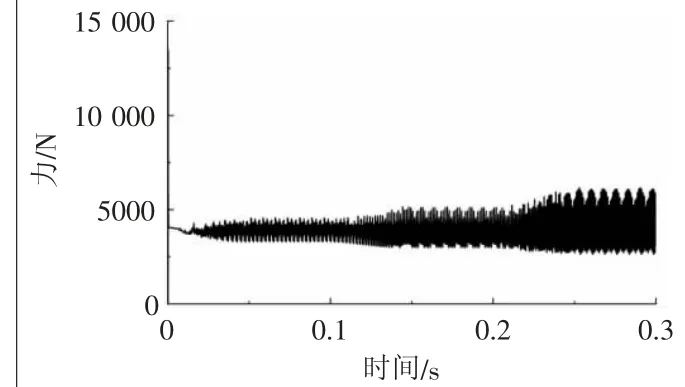
图3 变转速下齿轮接触力变化曲线

1.3 变负载工况齿轮动态特性分析

上节讨论的是当负载为恒定值时，转速对冲击的影响。重载无人机在实际飞行中，由于负载随飞行高度、环境及实际工作需求而变化，需要研究变负载条件下无人机弧齿锥齿轮所受冲击影响。因此，将负载函数设置-30 N、-70 N、-100 N 的阶梯函数，即STEP(time,0,0,0.03, -30) +STEP (time,0.1,0,0.13, -40) +STEP (time,0.2,0,0.23,-30)。被动大轮的啮合冲击力随负载变化如图4所示，由于速度为恒定值，啮入阶段会产生较大的冲击力，之后会以某一定值做一定范围的波动，随着负载的增加，由于齿轮重合度的增大，齿轮传动逐渐趋于平稳，波动幅度明显减小。

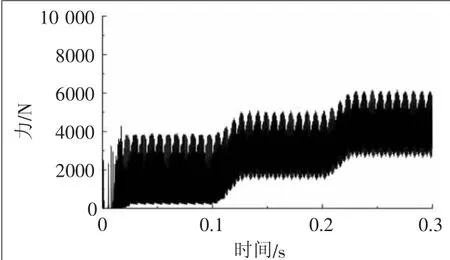
图4 变负载下齿轮接触力变化曲线

无人机实际工作中的情况正好相反，起飞时齿轮所受的冲击影响主要受转速的突增而增大，起飞后一段时间由于无人机满载，齿轮的重合度达到最高[7]，此时飞行最平稳。当无人机执行任务（如承载弹药对目标区域进行轰炸）时，其载重会瞬间减小，旋翼的负载也随之减少，连接旋翼的弧齿锥齿轮会瞬间受到较大的冲击，严重时可能导致轮齿折断从而使无人机坠毁。因此在设计无人机工作目标时，需要考虑无人机的初始承重及减重的分配。

2 弧齿锥齿轮固有特性分析

弧齿锥齿轮在运转时由于同时受到内、外部振动及循环加载力的影响, 可能导致振动频率接近固有频率[8]，引发机械共振，从而引起齿轮产生极大的变形和动载荷，最终导致轮齿破坏。为避免齿轮发生共振，需要对齿轮进行模态分析。

2.1 模态分析理论

模态为系统按照某一阶固有频率发生振动时各个点偏离平衡位置的位移比例关系的向量，它反映了机械结构固有的振动特性。模态分析过程的本质通过软件模拟或实验分析对每一个模态的固有频率、阻尼比及模态振型进行计算的过程。根据结构力学，机械系统动力学的运动方程为[9]

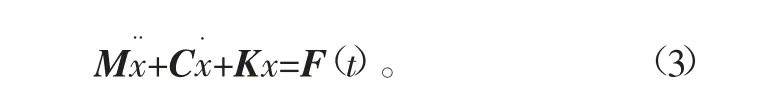
式中：M为机械系统的质量矩阵；C为机械系统的阻尼矩阵；K为机械系统刚度矩阵；x..为机械系统的加速度常量；x.为机械系统的速度常量；x为机械系统的位移常量；F（t）为机械系统的外部载荷向量。

当机械系统处于不受外力影响的自由振动情况，有F（t）=0，因此在计算运动方程时可忽略阻尼对系统的影响，此时系统无阻尼自由振动方程为

机械系统的振动方式为简谐振动，其振动位移方程为

式中，ω为模态固有频率矩阵，ω=[ω1ω2...ωn]，n为模态的阶数。

代入运动方程，可得特征值方程：

式中，x为由各阶固有频率振型组成的特征矩阵，表明自由模态的分析过程即为求解该特征值的过程。

2.2 有限元分析前处理

在弧齿锥齿轮的模态分析过程中，齿轮的固有频率和振型均为其固有特性，影响其主要原因为齿轮结构的质量和刚度要素在其结构中的分布，其分析结果与外部的载荷没有关联，因此在网格单元类型的选取上采用四面体网格划分，使质量与刚度元素在齿轮结构中均匀分布，提高结果的准确性。

当齿轮产生机械振动时，由于低阶固有频率及对应的振型相对容易出现，对齿轮系统的影响较大，而高阶固有频率下的振动会随着阻尼的作用而迅速减小。因此为提高分析效率，本文仅对齿轮的前6阶固有频率进行分析。

2.3 齿轮有限元模型建立及模态结果分析

将三维模型导入ANSYS Workbench，定义属性后使用分析步求解小轮的前六阶振型如图5所示，各阶对应的固有频率如表1所示。由图可以看出第一阶为圆周振动，其变形程度由内孔向齿轮大端逐渐增大，由于未施加外部载荷，因此该阶段固有频率接近0；第二、三阶模态表现为绕自身Y轴的摆动，最大变形发生在齿轮的大端靠近齿根侧；第四、六阶模态表现为弯曲振动，其最大变形发生在齿轮最大弯曲时的大端尾部；第五阶模态表现为扭转振动，其最大变形发生在齿轮沿轴向发生最大扭转时的齿轮大端根部。

图5 小齿轮前6阶振型图

根据表1中齿轮各阶模态下的数据可知，除第一阶模态外，最低固有频率发生在小轮的第二阶振型，其值为16 286 Hz，在进行无人机传动系统设计的过程中，应尽量避开此频率，防止发生共振导致齿轮破坏。

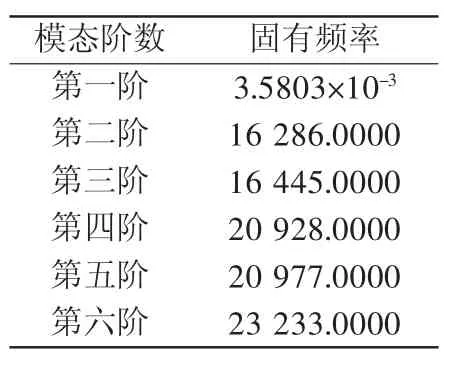
表1 小齿轮前六阶固有频率 Hz

3 结语

1）根据Hertz理论建立Impact函数，利用UG的Adams求解器对齿轮进行动态特性分析。首先定义齿轮之间的运动约束与接触，探究了不同转速条件下齿轮所受冲击的影响，研究发现，随着小轮转速的增加，被动大轮的转速产生周期性波动，且上下波动幅度及波动频率随之增大，产生的啮合冲击影响也逐渐增大；齿轮的啮合冲击力及冲击波动范围也随转速的增大而增大。在重载无人机传动时，应尽量避免在高转速附近运动，防止发生疲劳破坏。

2）研究了不同负载下齿轮所受冲击的影响，起初由于传动系统空载或轻载，齿轮啮合的重合度小于稳态重合度，此时齿轮啮合力波动范围较大，随着负载的增加，齿轮重合度增大，齿轮所受冲击的波动范围逐渐减小。无人机在工作时，由于需要进行卸载，会产生较大的冲击，为避免轮齿折断导致无人机无法工作，应考虑在卸载时适当增大外部负载（如改变飞行姿态）。

3）以小轮为例，使用ANSYS分析得到齿轮的前6阶模态，得到了模态振型及对应的固有频率，在无人机工况设计中，应尽量避开此频率，防止发生共振导致齿轮破坏。