直剪试验下粗粒土能量演化与强度参数关系研究*

荀晓慧 何 亮 贺晓东

(①地质灾害防治与地质环境保护国家重点实验室(成都理工大学)， 成都 610059， 中国)

(②华杰工程咨询有限公司， 北京 100029， 中国)

0 引 言

粗粒土作为建筑材料，多用于土石坝、公路、铁路等建筑工程，其强度参数是决定工程设计的关键指标之一。前人学者利用不同方法对粗粒土的抗剪强度特性开展过研究，其中：能量守恒作为自然界普遍适用规律，可从本质上探究剪切过程中的土体状态变化，定性及定量描述抗剪强度的发挥过程。基于能量角度，Taylor(1948)提出了粗粒土抗剪强度机理的两分量学说，认为抗剪强度是由土颗粒间的摩擦阻力、土体剪胀而产生的颗粒间相互作用力两部分形成。Rowe(1962)基于对砂土的研究，分析能量平衡方程，认为抗剪强度由颗粒滑动摩阻力所发挥的强度、重新定向和重新排列所需能量而发挥的强度、剪胀耗能而发挥的强度3部分组成。抗剪强度主要受颗粒间的摩擦、剪胀、颗粒重新排列和破碎这4种因素的影响(日本土质工学会， 1999)。Hettiarachchi et al.(2009)从能量平衡角度，采用标准渗透测试(SPT)吹气计数估算了土的剪切强度。Saurer et al.(2011)基于MATLAB分析模型的断裂力学能量平衡和极限平衡方法，定性和定量地模拟非平面剪切带传播速率。剪切过程中具有明显的能量演化特征，基于能量耗散机制下，能量发生着传递与耗散(陈旭光等， 2010； 蒋明镜等， 2013)，采用轴向应力比例的能量分析法，可实现对各阶段能量变化趋势进行深入研究(陈国庆等， 2018)。王伟(2006)采用能量耗散原理研究了土与结构面接触模型及应用。何亮等(2019)基于能量耗散机制下，对直剪试验中粗粒土的圆度损伤演化与能量耗散过程进行了研究，通过结合热力学定律建立了圆度损伤模型，定性及定量地分析了直剪试验下粗粒土能量演化与圆度损伤特性。汤连生等(2006)将能量状态-结构熵进行量化。直剪试验下粗粒土的剪切过程中，刘斯宏等(2001)分析了剪切框受力变化，提出了剪切盒内壁摩擦对剪切强度影响。徐永福(2018)充分考虑了颗粒破碎对粗粒土的直剪试验的影响，颗粒破碎对剪切强度的破碎准则有影响，认为颗粒未发生破碎的试样，直剪试验下剪切强度符合Mohr-Coulomb 准则，颗粒在剪切过程中产生破碎，其强度包络线呈显著的幂函数关系。

目前，针对粗粒土的试验研究，多集中于从颗粒破碎、形状、运动等角度对其力学特性变化进行研究，未系统地从粗粒土剪切过程中能量守恒角度，研究其能量演化与强度参数关系，并建立一定程度上具有普适性的函数模型。本文基于能量守恒原理定性及定量对能量演化过程与强度参数关系做出研究，是有效描述粗粒土强度本质的一种有意义的尝试。通过利用能量守恒原理，研究剪切初始-峰值应力阶段，结合粗粒土直剪强度特性，建立了基于系统能量守恒下的能量演化与强度参数关系理论模型，基于假定条件下提出适用模型，对模型进行论证与应用探讨，分析了能量演化过程对粗粒土的力学特性响应，具有一定的理论指导意义和工程实用价值。

1 直剪试验剪切过程中能量演化分析

1.1 基于能量守恒下的功能转换关系

粗粒土直剪试验下的剪切过程满足能量守恒定律，能量以一种形式转换成另一种形式。剪切盒表部受水平力做功(WFi)、竖向力作功(WF1)，剪切达到峰值应力时，水平方向存在一瞬时速度V1，竖直方向瞬时速度V2。剪切框动能增量ΔEK1，盖板动能增量ΔEK2，盖板重力势能EP1。下部剪切盒在四周约束条件下静止，剪切盒为刚性，不考虑剪切盒的变形能。荷载传到粗粒土内部经功能转换，形成直剪试验下粗粒土内部复杂的能量转换过程(图1)。

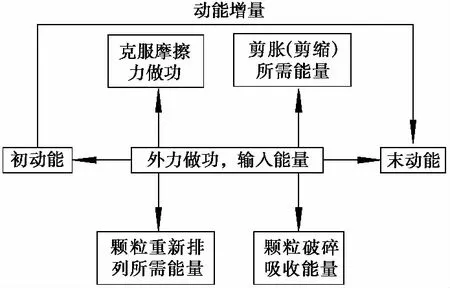
图1 功能转换关系图

一部分能量克服摩擦力做功Wf，以磨损形式散失，基于热力学第二定律(秦允豪， 2011)知摩擦生热为不可逆过程，致使系统整体能量逐渐减少； 一部分转换为颗粒剪胀(剪缩)的所需能量E剪，宏观体现在颗粒孔隙率增大(减小)； 一部分转换为颗粒间重新排列所需能量E排，具体表现为粗粒土在剪切盒内以错动、翻滚、掉落等形式产生动能与势能； 基于最小耗能原理(周筑宝等， 2017)，另一部分因颗粒破碎吸收部分能量E碎。直剪试验下粗粒土抗剪强度由克服摩擦力做功发挥的强度、剪胀(剪缩)发挥的强度、颗粒破碎发挥的强度、颗粒间重新定向排列所发挥的强度4部分。基于系统能量守恒下，可知直剪试验下系统能量演化过程满足基本理论准则：

WFi+WF1=ΔEK1+ΔEK2+EP1+Wf+

E剪+E排+E碎

(1)

式中：WFi、WF1分别为剪切盒表部受水平力和竖向力做功； ΔEK1为剪切框动能增量； ΔEK2为盖板动能增量；EP1为盖板重力势能；Wf为克服摩擦力做功；E剪为颗粒剪胀(剪缩)所需能量；E排为颗粒间重新排列所需能量；E碎为颗粒破碎吸收的部分能量。

1.2 试验过程中能量变化

传统直剪仪剪切过程，理想状态下可简化为基本物理问题进行分析，在水平压强Pi、竖向压强Pm作用下，上部剪切盒沿剪切方向运动，系统总质量M，地面对系统支撑反力N，受到摩擦力f1阻碍上部剪切盒沿剪切方向运动(图2)。

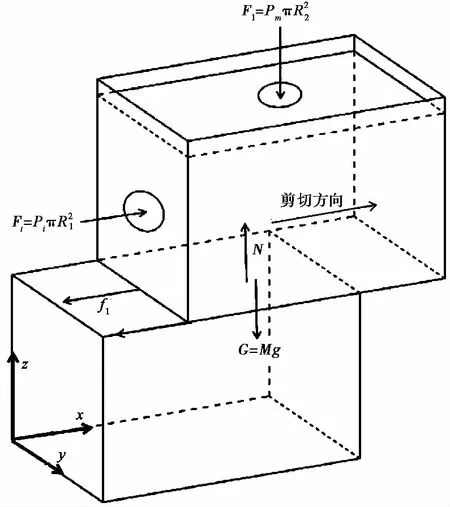
图2 理想状态下基本受力简图

剪切初始-峰值应力阶段能量变化，从系统能量守恒的角度分析直剪试验的功能转换，研究抗剪强度更准确、合理。剪切初始-峰值应力阶段，上部剪切盒距原点水平位移xi，沿剪切方向。因剪胀(剪缩)盒内颗粒孔隙率增大(减小)，促使盖板竖向运动，初位置在z轴上距原点Z1，末位置Z2。

(2)

式中：Pi为水平压强； π为圆周率；R1为水平加压装置油缸半径；n为水平加压的阶段总数量；xi为上部剪切盒距原点水平位移。

(3)

式中：Pm为竖向压强；Z1、Z2分别为盖板竖向运动时距原点的始末距离；R1为竖向加压装置油缸半径。

(4)

因内部颗粒剪胀、重排列、破碎致使剪切框与盖板存在重力势能改变：

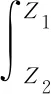
(5)

式中：g为重力加速度。

剪切过程中摩擦受力复杂，主要来源于剪切框间摩擦、剪切框与盖板间摩擦(剪胀与剪缩摩擦受力方向相反)、剪切框与颗粒间摩擦(考虑牛顿第一定律)(腾保华等， 2017)、剪胀、剪缩条件下上部剪切框后板受力不确定)、颗粒间相互摩擦(颗粒运动过程中接触面积持续变化)、颗粒与平台板间摩擦。考虑摩擦作用的不确定性，根据摩擦学中能量磨损理论(温诗铸等， 2008)可知，磨损是能量转换和消耗的过程。直剪试验中剪切过程克服摩擦力做功大部分以摩擦热形式散失，满足随时间变化的函数，用Q(t)表示； 小部分以势能形式存储在颗粒间，达到临界状态以磨屑形式从表面剥落，用E1表示。

Wf=Q(t)+E1

(6)

式中：Q(t)为随时间变化的摩擦热函数；E1为达到临界状态以磨屑形式剥落具有的势能。

剪胀(剪缩)消耗的能量、颗粒重新定向排列所需能量，宏观体现在颗粒形成复杂运动与孔隙率增大，达到峰值剪应力时，因颗粒运动速度不定向，根据运动学中运动叠加原理(腾保华等， 2017)，剪切盒内颗粒瞬时速度在坐标系下可表示为：

(7)

式中：v为剪切盒内任意颗粒瞬时速度；i、j、k为单位常矢量；t为作用时间。

瞬时速度大小可表示为：

(8)

有n1个颗粒，质量为mk产生平动动能，有n2个颗粒剪切过程中产生转动动能，有n3个质量为m′i的颗粒在剪切过程中产生重力势能，初位置距原点高度Z′1j，末位置Z′2j。

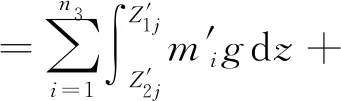
(9)

式中：n1、mk分别为产生平动动能颗粒数量和质量；n2为产生转动动能颗粒数量；n3、m′i分别为产生重力势能颗粒数量和质量；Ixj、Iyj、Izj和θxj、θyj、θzj分别为x、y、z方向转动惯量和转动角度。

基于最小耗能原理(最小熵产生原理)(周筑宝等， 2017)，颗粒破碎时，应力集中现象被释缓，系统中任意时间t的总耗能率为：

(10)

式中：Φ为系统总能耗率；V为体积；T、Jk、Xk分别为微小单位体积在瞬时t的绝对温度、相对应的“流”、相对应的“力”。

总耗能率为随时间函数，对总耗能率积分得：

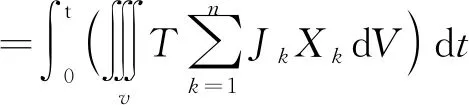
(11)

综上所述，基于能量守恒下直剪试验能量演化过程可表示为：

(12)

从推导的基于系统能量守恒下的能量平衡方程可知：剪切系统从启动至达到峰值应力整个阶段，直剪试验下系统能量变化包括外力做功、克服摩擦力做功、平动及转动动能、颗粒破碎吸收能量、增减的势能。整个阶段，系统受力情况复杂且持续变化，根据力的相互作用原理，颗粒间受力随剪切过程而变化。

2 能量与强度参数关系

2.1 关系模型的建立

能量守恒是建立直剪试验下能量演化与强度参数关系的根本准则。传统直剪试验测得的强度参数值，基于剪切面为平面、应力分布均匀、试样受力面积为定值、正应力不考虑偏心受压等基本假设下，使试验值存在误差(张敏江等， 2005； 徐进等，2008)，为建立强度参数与能量演化关系，需对比考虑理想状态下强度参数取值与实际取值误差分析。剪切达到峰值应力临界状态，满足莫尔-库仑破坏准则：

τf=c+σtanφ

(13)

式中：τf为抗剪强度；c为黏聚力；φ为内摩擦角；σ为正应力。

(14)

式中：τ′f、σ′分别为修正的抗剪强度和正应力；A1、A2分别为试样剪应力、正应力作用受力面积。

定义：

(15)

式中：γ、β为修正影响系数。

传统直剪试验认为：达到峰值应力时，满足莫尔-库仑强度准则(式13)。

(16)

式中：A2为正应力作用受力面积。综合上述分析，将式(16)代入式(12)，可建立Pi、Pm、c、φ间基于能量守恒下理论关系式：

(17)

上式为达到剪切峰值临界状态时能量演化与强度参数间关系理论模型，也是直剪试验影响粗粒土强度参数取值的根本准则，不同类型粗粒土基于直剪试验下的剪切达到峰值均满足此理论方程，当剪切达到临界应力峰值时此理论模型成立。

因式(17)中各项能量消耗作用中的参数仍是概念性的，对于散粒集合的多自由度体系，各参数难以具体量化，因此提出如下假定：(1)剪应力分布均匀，竖向荷载发生偏移产生弯矩不计； (2)剪切破坏面视为上下剪切盒间平面； (3)剪切过程上部剪切框及颗粒其速度恒定； (4)除剪切核心区外剪切框顶部与底部颗粒间无相对运动； (5)颗粒间摩擦力在颗粒运动方向上无相对位移。

由式(17)可知，粗颗粒基于三维空间内运动、破碎等产生的能量较为复杂，视二维可观测面为x-y平面，将三维问题等效转换至二维平面进行研究，同时充分运用数学微积分思想，通过分析能量密度、二维破碎率等在空间内积分获得三维空间内能量(周健等， 2006； 吕超等， 2019； 马林建等， 2019)，定义函数E(t)：

(18)

剪切试验中颗粒总破碎率为P，基于可观测二维平面破碎率P1，为颗粒破碎耗能占能量演化总能量比值。因剪切盒内壁光滑，颗粒间接触多为点-点接触、点-面接触，对于棱角数较多、磨圆度较好颗粒，颗粒间摩擦力在颗粒运动方向上无相对位移，Q(t)、E1趋于无穷小。基于二维可观测面其颗粒运动、破碎等总能量E1(t)可表示为：

(19)

式中：P1为基于可观测二维平面破碎率。

式(19)中破碎率P1； 产生重力势能、转动动能、平动动能颗粒数：n′1、n′2、n′3； 质量m′i、mk； 时间tj、tk； 位移xk、yk、z′1j、z′2j； 角度θxj； 转动惯量Ixj均可由试验分析计算获得，重力加速度g均为已知量取9.8m·s-2。

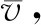
(20)

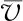
(21)

根据式(18)～式(21)可解得E(t)：

(22)

将式(22)代入式(17)中，取γ=1.02，β=1.0(张敏江等， 2005)得到式(23)：

(23)

能量的定量变化是影响粗粒土强度参数取值的根本因素，基于假定条件下的剪切峰值临界状态时能量演化与强度参数间关系适用模型，未定量数据均可根据试验测定。

2.2 模型的论证与分析

同一直剪系统下，达到剪切峰值临界状态一定，定义等式(23)左半部分为剪切达到峰值最后一阶段外力做功能量函数F(c，φ)：

(24)

式(24)以c、φ为自变量，F(c，φ)为因变量的二元一次函数。

定义等式(23)右半部分为函数G(c，φ)：

(25)

为方便计算c、φ与证明模型，运用反算法，假设试验获得强度参数值c、φ为已知量满足式(23)，必然有基于不同法向应力下F(c，φ)=G(c，φ)，则假设成立，公式得以证明。

颗粒间接触方式对研究颗粒运动具有重要意义(程展林等， 2007； 王子寒等， 2018)，本文以颗粒表面磨圆度为主要指标，选择棱角型接触(花岗岩等，图3)和圆型接触(鹅卵石等，图4)两种类型粗粒土，研究从剪切初始-峰值阶段的能量演化与强度参数取值间关系。

图3 棱角型接触

图4 圆型接触

粗粒土颗粒的形状差异对其力学特性产生较大影响(张斌等， 2020； 朱遥等， 2020)，且不同类型粗粒土的材料性质存在一定程度上的差异，在剪切试验过程中，主要表征于颗粒破碎、平动、转动、磨损等难易程度存在差异。因此不同类型粗粒土(棱角型、圆型)的能量演化过程，在一定程度上响应了其材料性质的差异，可较好地论证该模型的准确性及普适性。同时为减小颗粒间及试样间尺寸效应影响，控制试验所用粗颗粒最大高度不超过剪切盒高度的1/20(谭彩等， 2016)，约束单个颗粒最大粒径D≤10mm，采用剪切盒规格为200mm×200mm×200mm的改进可视化直剪仪(图5)。

图5 改进可视化直剪仪

试验设备部分技术参数如表1所示：

表1 试验设备技术参数

试样截面积取值A1=A2=0.03m2，π=3.14，F(c，φ)可化简为：

F(c，φ)=0.0306cΔx+0.072063PmtanφΔx

(26)

将制备的棱角型和圆型接触两类粗粒土材料，依次采用夯填的方式装入可视化剪切盒中，使其具备一定的密实度。在对直剪仪上承压板、竖向及水平荷载施加装置、百分表、摄影系统等进行调试结束后，通过分级施加剪切荷载，对棱角型、圆型接触两类粗粒土分别开展法向应力为100kPa、200kPa、300kPa的室内试验。根据剪切试验数据，获得应力-应变曲线(图6)及应力-位移统计表(表2)。

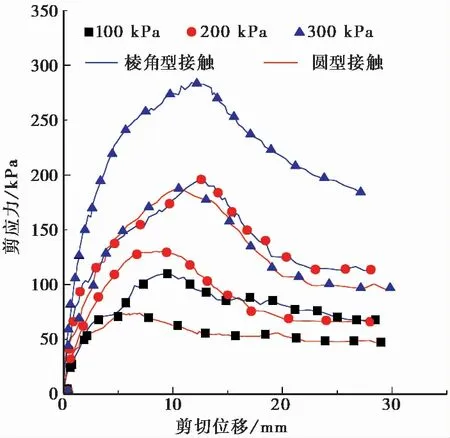
图6 两类粗粒土在不同法向应力下应力-应变关系曲线

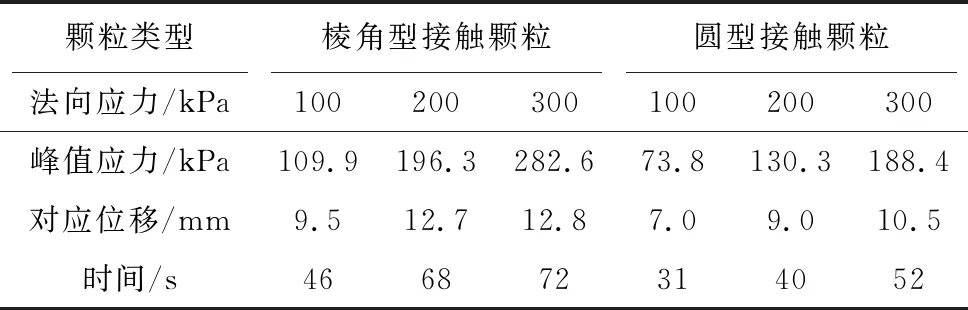
表2 峰值应力-位移统计

通过整理试验数据，得到不同类型颗粒各组试样破坏时的库伦强度拟合直线，由室内试验得到数值拟合曲线(图7)。

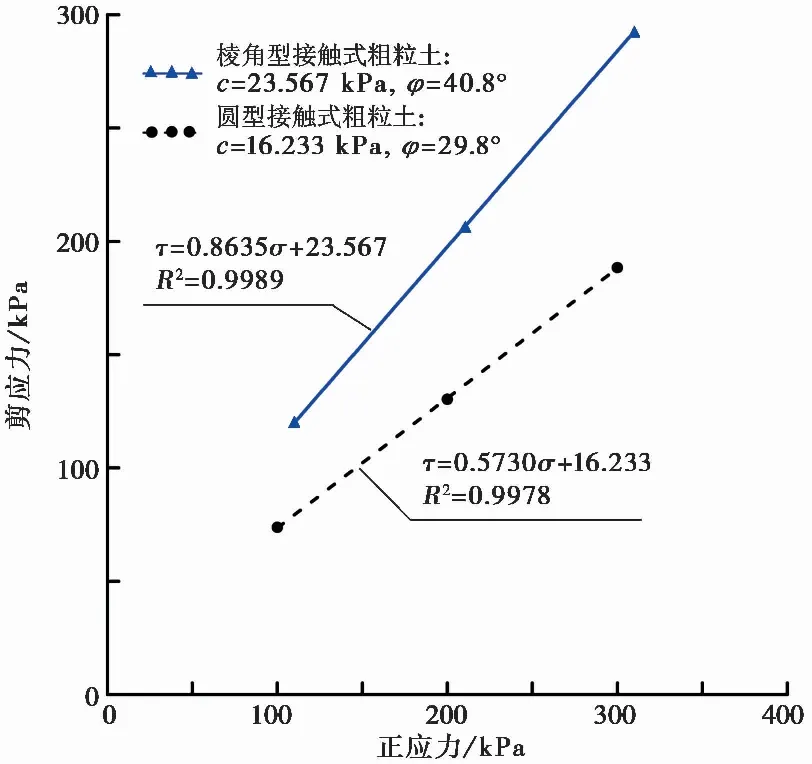
图7 两类粗粒土强度拟合直线

由试验数据可知，两类粗粒土达到峰值应力时水平加压的阶段总数量n、位移增量Δx在不同法向应力下取值如表3所示：

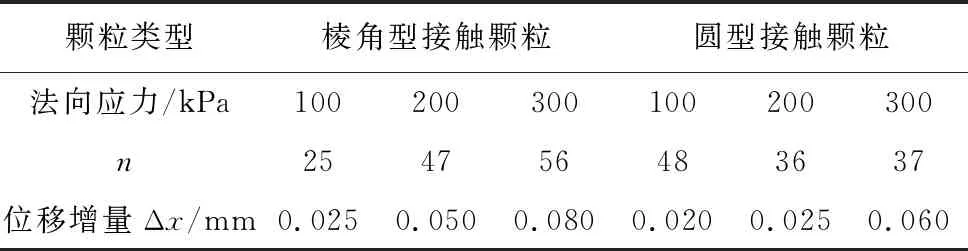
表3 不同法向应力下n、Δx取值

根据式(26)可计算棱角型接触式、圆型接触式粗粒土法向应力分别为100kPa、200kPa、300kPa时F(c，φ)值(图8)。

图8 正应力与F(c，φ)关系图

由图8可知，剪切达到峰值应力时，在相同法向应力下，因棱角型颗粒更易产生运动状态的改变，棱角型颗粒最后一阶段外力做功F(c，φ)值大于圆型颗粒，针对同种颗粒，因法向应力对颗粒运动状态改变具有束缚作用，从而影响能量变化，F(c，φ)随正应力值增加而增大。

对式(23)中G(c，φ)计算，针对可观测面上粗粒土，因颗粒数量较多，运用统计学原理(郑志刚等， 2016)，统计棱角型、圆型基于可观测面颗粒样本总数N1=304、N2=316。转动动能主要产生于剪切带内，运用image-pro图像分析软件，可获得两种类型颗粒在100kPa、200kPa、300kPa法向应力条件下剪切前后颗粒转动角度等信息。此处主要针对200kPa法向应力试验条件下的图像识别结果进行分析(另外两级法向应力条件下的图像识别处理方法与此一致)，获得棱角型、圆型接触式粗粒土长轴方向角度变化分布的柱状图(图9、图10)。

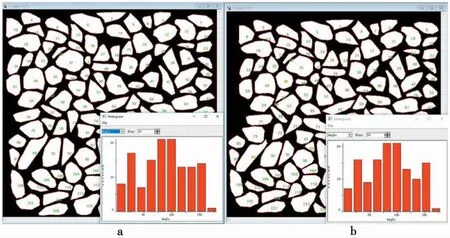
图9 棱角型接触式粗粒土角度长轴方向分布

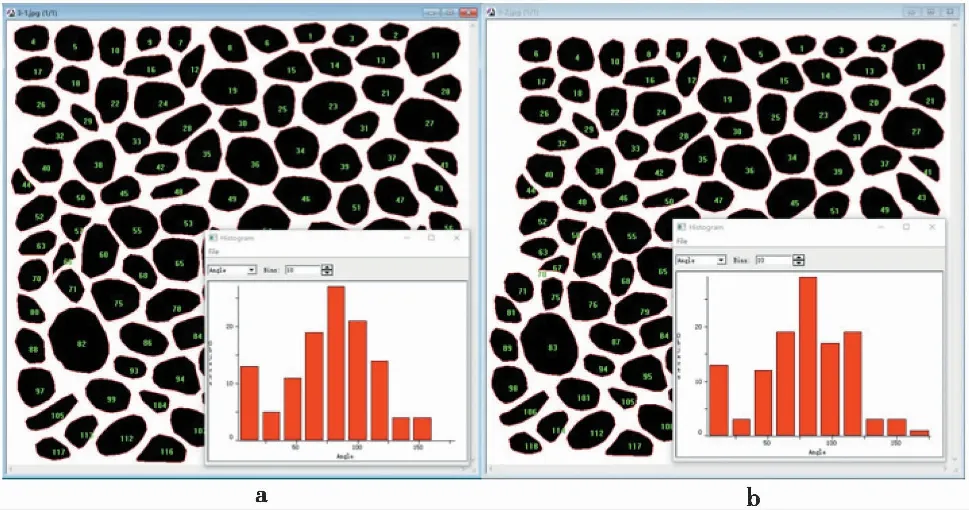
图10 圆型接触式粗粒土角度长轴方向分布

相较于初始应力状态，应力峰值时颗粒长轴方向分布于1°～90°角度范围内颗粒增多， 90°～180°角度范围内颗粒逐渐减少。因其能量演化遵循最小阻力途径传递，根据消耗途径的难易程度进行选择，沿着最易路径进行传递，其棱角型颗粒表现尤为明显。圆型接触颗粒表面无不规则突出棱角，受粒间接触应力、受力面积等影响不足以使其产生明显转角。

针对样本数总数内颗粒统计其运动情况如图11所示：

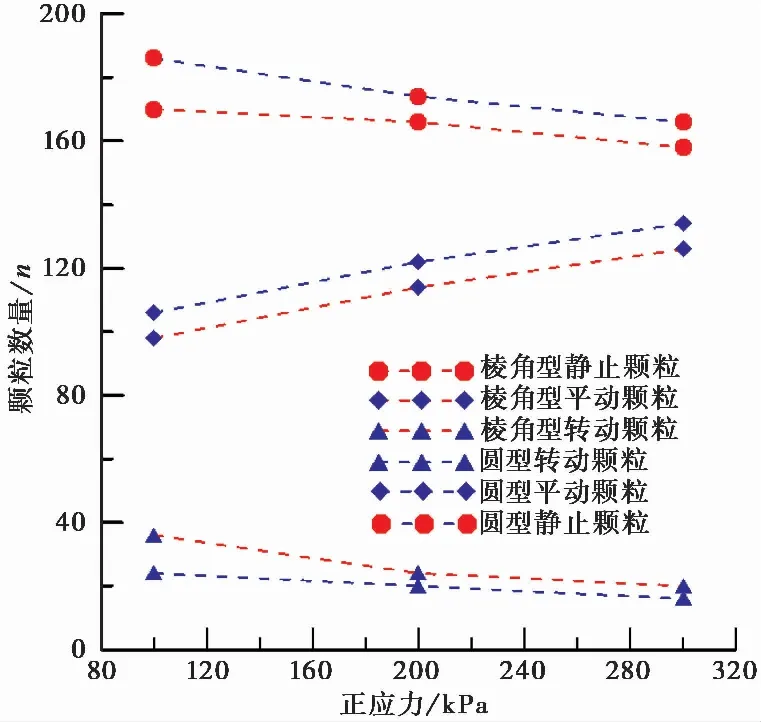
图11 颗粒运动情况统计图

通过分析颗粒运动分布情况，因重力势能颗粒产生竖向运动伴随颗粒转动同时存在，因此m′i为产生转动颗粒总质量。将颗粒矢量化于CAD中求得对应颗粒Ixj，运用Image-Pro得到θxj。为简化计算过程，利用MATLAB计算G(c，φ)极限值，计算法向应力分别在100kPa、200kPa、300kPa下棱角型及圆型颗粒函数取值如图12所示。在不同法相向应力下，F(c，φ)取值在G(c，φ)最值范围内，当能量取值精度为0.01J时，F(c，φ)=G(c，φ)，因此假设成立。棱角型颗粒与圆型颗粒其强度参数按照理论模型计算取值与试验值相等，剪切峰值临界状态时能量演化与强度参数间关系适用模型成立。

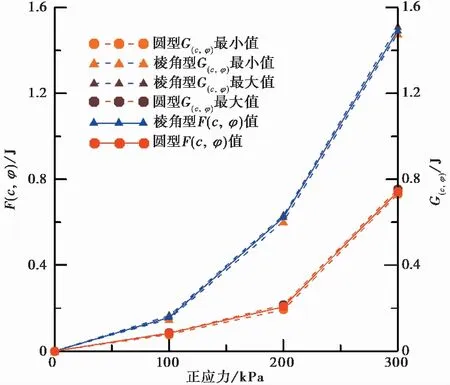
图12 不同法向应力下F(c，φ)与G(c，φ)最值关系图

根据试验过程能量演化分析，获得不同法向应力下，直剪试验下达到应力峰值时最后一阶段外力做功与强度参数值三维关系图(图13)。

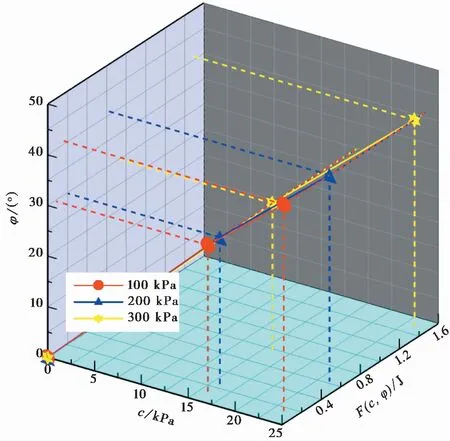
图13 最后一阶段外力做功与强度参数值关系图

同一法向应力下，最后一阶段外力做功F(c，φ)随强度参数值c、φ增加而增大，F(c，φ)分别与c、φ呈线性关系。强度参数c、φ值越大，剪切过程中颗粒能量演化越剧烈。

3 模型的应用探讨

对式(24)取微分，针对同一类颗粒在特定的直剪系统，以c、φ为自变量，f(c，φ)为因变量，可化简为f(c，φ)与c、φ的二元一次函数。为剪切峰值临界状态外力变化函数方程：

(27)

采用MATLAB对函数进行分析，绘制f(c，φ)函数图像(图14)，图14反映了直剪试验下粗粒土c、φ值与函数f(c，φ)间关系，针对一特定f(c，φ)值，c、φ间有多种线性组合，分别以c、φ为定值，函数值均呈抛物线增大。整体随着c、φ值增大，f(c，φ)函数值呈抛物面趋势增大。根据信息数据提取并标记，棱角型接触式粗粒土f(23.567， 40.8)>圆型接触式粗粒土f(16.233， 29.8)，通过直剪试验结果表明，棱角型接触式粗粒土强度参数值大于圆型，其抗剪强度大。可推广至不同类型粗粒土，实验测定的强度参数值大，对应f(c，φ)值偏大，且呈抛物线增大，最终收敛于定值f(cα，φβ)。

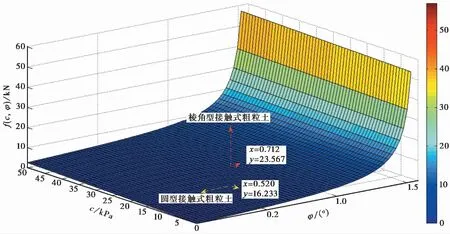
图14 f(c，φ)函数图像

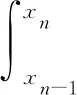
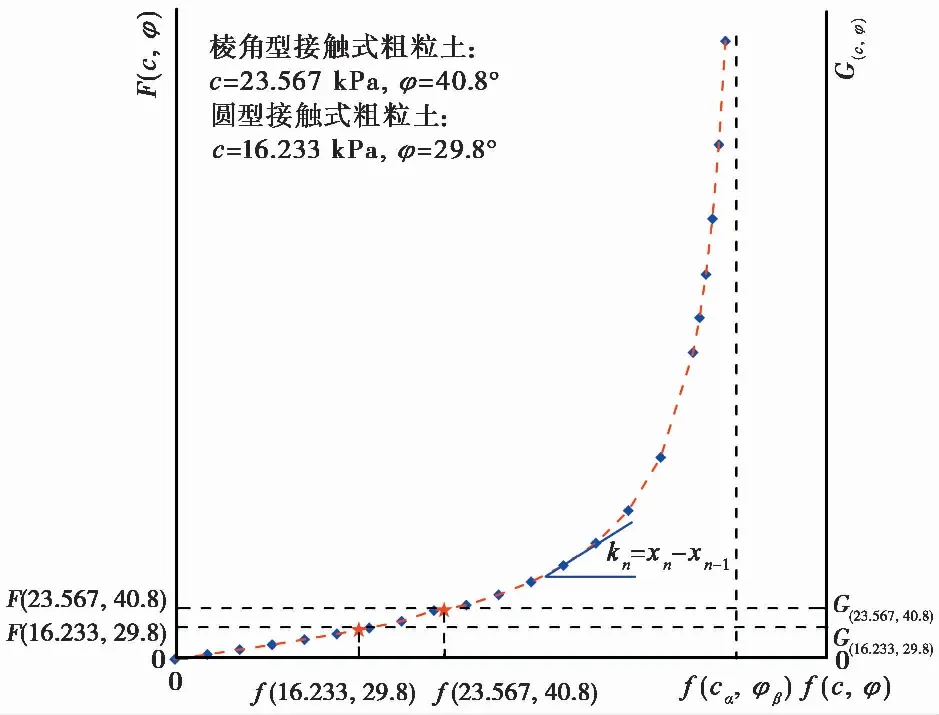
图15 f(c，φ)与F(c，φ)，G(c，φ)函数关系图

F(c，φ)以斜率kn=xn-xn-1呈抛物线递增，试验表明棱角型接触式粗粒土抗剪强度大于圆型接触式粗粒土，满足f(c，φ)值增大，F(23.567， 40.8)>F(16.233， 29.8)，随因变量持续增大自变量会无限收敛于定值f(cα，φβ)。

综合上述分析，粗粒土作为铁路路基的主要填料，颗粒表部受到列车轨道传递的竖向荷载时，内部颗粒受剪，使其路基发生剪切破坏(龙尧等， 2017)。受力情况根据相似定律可类比于粗粒土直剪下粗粒土直剪试验，当忽略产生弯矩等情况，在受力过程中，选择强度参数值较大颗粒(棱角型)其剪切破坏所需能量较大，更不易发生破坏。通过室内试验可求得材料强度参数值，达到临界峰值应力时，强度参数c、φ值与其能量演化满足式(17)的理论模型，通过约束相关条件亦满足式(23)的适用模型。当选取作为路基填料的粗粒土强度参数持续增加，其剪切破坏临界状态外力增大，无限收敛于一定值，对应能量也逐渐增加。可通过探索这一极限值f(cα，φβ)，选取强度参数值最理想的材料作为路基填料，达到相应工程要求。

4 结 论

通过研究直剪试验下粗粒土强独特性与能量演化过程，结合热力学定律与Mohr-Coulomb强度准则，建立能量演化与强度参数关系模型，采用试验验证了模型的正确性与适用范围，定性及定量地描述了能量演化与强度参数间关系。对模型深入分析，运用MATLAB分析函数，对其应用进行探讨。得到如下结论：

(1)直剪试验下能量演化与强度参数理论模型，剪切达到临界应力峰值时此理论模型成立。提出基于假定条件下的能量演化与强度参数间关系适用模型，当能量取值精度为0.01J时模型成立。

(2)棱角型接触颗粒其强度参数取值相较于圆型颗粒大，主要原因为剪切过程能量演化过程愈剧烈，颗粒转动动能等较大，达到应力峰值临界状态外力做功能量值增大。

(3)不同法向应力下，最后一阶段外力做功F(c，φ)随强度参数值c、φ增加而增大，F(c，φ)分别与c、φ呈线性关系。强度参数c、φ值越大，剪切过程中颗粒能量演化越剧烈。

(4)文中提出的能量演化与强度参数模型，可用于分析工程中路基填料受剪情况下使其破坏的最大剪应力与能量。当选取作为路基填料的粗粒土强度参数值持续增加，其剪切破坏临界状态外力增大，无限收敛于一定值，对应能量也逐渐增加。可通过探索这一极限值f(cα，φβ)，选取强度参数值最理想的材料作为路基填料，达到相应工程要求。