Ni-Co-Cr基粉末高温合金动态再结晶的有限元模拟与实验研究

乔世昌，王岩,3，吕良星，谭钢，杨雷，黄钲钦，李慧中

（1.中南大学粉末冶金研究院，湖南长沙，410083；2.中南大学粉末冶金国家重点实验室，湖南长沙，410083；3.哈尔滨工业大学金属精密热加工国家级重点实验室，黑龙江哈尔滨，150001；4.哈尔滨工业大学空间环境与物质科学研究院，黑龙江哈尔滨，150001；5.中南大学材料科学与工程学院，湖南长沙，410083）

镍基粉末高温合金具有较大的单轴强度及较好的抗疲劳性能、抗蠕变性能和抗氧化性能，已广泛应用于航空航天领域[1]。镍基粉末高温合金的制备工艺主要包括粉末制备、热固结、热变形（热挤压或热锻造）以及热处理[2-3]，其中，热变形作为制造粉末高温合金的关键工序，一直是镍基粉末高温合金领域的研究热点[4-8]。许多学者结合热模拟方法对镍基粉末高温合金的热变形行为进行了实验研究，如：WU 等[4]研究了热等静压（HIP）态FGH100高温合金在1 050～1 150 ℃和0.001～1 s-1条件下的热变形行为，建立了本构方程并基于动态材料模型理论构建了热加工图，确定了合适的热加工参数；XU 等[5]研究了HIP 态FGH96 合金的热压缩行为，获得了合金的变形热激活能，并分别给出了合金动态再结晶动力学和动态再结晶平均晶粒粒径公式；刘建涛等[6]研究了HIP态FGH96合金的动态再结晶行为，发现应变速率显著影响合金的动态再结晶晶粒粒径，并建立了动态再结晶平均晶粒粒径与参数Z之间的关系，构建了合金的动态再结晶状态图；KUMAR 等[7]利用等温热压缩实验研究了一种新型HIP态粉末高温合金在热变形过程中的微观组织演变，基于EBSD分析了合金的动态再结晶行为，发现在低变形温度和高应变速率下合金的动态再结晶过程受到抑制；TAN等[8]研究了一种HIP态镍基粉末高温合金在高应变速率下高温压缩的微观组织演变，发现合金在高应变速率下的不连续软化现象明显，这主要源于动态再结晶的作用。综上可见，目前对于镍基粉末高温合金热变形行为的实验研究主要集中于热等静压态，而关于热挤压态合金相关研究很少[9]。合金的初始状态会对其热加工行为产生重要影响，因此，展开对热挤压-退火态Ni-Co-Cr基粉末高温合金动态再结晶行为的研究具有重要意义。有限元（FE）数值模拟是塑性加工成形研究中最为有效的方法之一，对于优化热变形工艺参数、理解热加工过程中的微观组织演变、降低研制成本具有十分重要的意义，已在高温合金热变形研究中得到广泛应用[9-11]，然而，目前结合FE方法研究粉末高温合金热加工行为的报道还很少。刘敏学等[12-13]对热挤压-退火态FGH96的热变形行为展开了研究，建立了本构方程和热加工图，提出了优化的热加工参数范围，同时构建了动态再结晶模型，利用Deform-3D 有限元软件模拟了合金的热压缩过程，通过与实验结果对比验证了模型的准确性。本文选用一种新型热挤压态Ni-Co-Cr 基粉末高温合金作为研究对象，对该合金进行退火处理以消除热挤压过程中形成的残余应力，系统研究热挤压-退火态Ni-Co-Cr 基粉末高温合金的热压缩行为，建立合金的动态再结晶模型，利用FE 方法对合金在不同条件下的热压缩过程进行仿真模拟和实验验证，分析合金的动态再结晶机制，以期为变形组织的控制和热锻工艺参数的优化提供理论依据。

1 实验

实验所用材料为新型挤压态Ni-Co-Cr 基粉末高温合金，热挤压温度为1 140 ℃，挤压比为9∶1，化学成分如表1所示。挤压态合金经900 ℃/2 h 均匀化退火处理后，其显微组织如图1（a）所示。由图1（a）可知退火态合金中的晶粒呈现等轴晶形貌。合金晶粒粒径统计结果如图1（b）所示，可见合金平均晶粒粒径约为10.21 μm。图1（c）所示为退火态合金中γ'相的形貌及分布情况，可见γ'相呈现近球形，分布均匀。

图1 热挤压-退火态Ni-Co-Cr基粉末高温合金的显微组织Fig.1 Microstructures of hot extruded-annealed Ni-Co-Cr-based PM superalloy

表1 实验用Ni-Co-Cr基粉末高温合金的化学成分（质量分数）Table 1 Chemical composition of experimental Ni-Co-Cr-based PM superalloy（mass fraction）%

经退火处理后的合金加工成直径×高为8 mm×12 mm 的圆柱试样，然后在Gleeble-3500D 热模拟机上进行高真空环境的等温热压缩实验，压缩实验装置如图2（a）所示。压缩前，在样品两侧涂抹润滑油并黏附石墨箔，以尽量减小压缩过程中试样与压头之间的摩擦。压缩实验温度分别为1 020，1 050，1 080 和1 110 ℃，应变速率分别为0.001，0.01，0.1 和1 s-1。压缩前以10 ℃/s 的升温速度将试样加热到设定温度后，保持120 s 以确保试样内部温度分布均匀，变形量为50%，真应变为0.693，实验流程如图2（b）所示。在压缩过程中，计算机自动收集真应力、真应变等参数；压缩结束卸载后立即水淬至室温，以保留合金高温变形组织。

将热压缩后的试样沿中心轴向切片，经研磨、机械抛光及腐蚀后分别在光学显微镜和配有电子背散射衍射（EBSD）专用软件（Oxford,Aztec）的场发射扫描电子显微镜SEM（FEI Quanta 650）上进行检测。晶界腐蚀剂成分为100 mL HCl+100 mL C2H5OH+5 g CuCl2，γ'析出相的腐蚀剂成分为33 mL HNO3+33 mL CH3COOH+33 mL H2O+1 mL HF。利用Image-Pro Plus（IPP）图像分析软件分别对不同变形制度下的动态再结晶体积分数和晶粒粒径进行测定，每种状态试样至少选择5张不同位置的照片进行定量测量，取其平均值作为最终结果。将机械抛光后的SEM试样进一步进行6～8 h振动抛光，再进行EBSD表征，步长设定为0.4 μm；采用channel 5软件对EBSD数据进行后续处理与分析。

利用Deform-3D软件对不同变形条件下圆柱试样的热压缩过程进行有限元模拟。由于Deform-3D软件中工件模型存在旋转和轴向对称性（如图2（c）所示），为了节省计算时间，取工件和压头的1/2用于建模，使用软件的镜像功能构建所需的几何图形并可视化，压缩后的模型如图2（d）所示。模具设定为刚性体，圆柱试样工件为塑性体，温度均设定为实验温度。上模具沿圆柱试样中心轴移动，移动速率为v（其中，v=˙×h，˙为应变速率，h为任意时刻下的试样高度）。工件材料的准确流动应力对于准确预测流动应力行为非常重要，数学模型选用（其中，为等效流动应力，为等效应变，˙为等效应变速率，T为变形温度），将实验流动应力导入软件中以定义材料的塑性变形行为。工件与模具间传热系数设置为11 N/（s·mm·℃），工件在热锻过程中不与模具的边界接触，与环境发生对流传热，设置环境温度20 ℃作为对流传热计算参考点，对流系数为0.02 N/（s·mm·℃）。

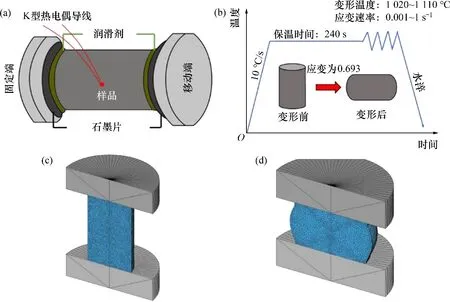
图2 热挤压-退火态Ni-Co-Cr基粉末高温合金热压缩实验及Deform模型Fig.2 Hot compression tests and Deform models of hot extruded-annealed Ni-Co-Cr-based PM superalloy

2 结果与讨论

2.1 流变应力曲线及其摩擦修正

热挤压-退火态Ni-Co-Cr基粉末高温合金在不同热压缩参数下的真应力-真应变曲线如图3所示。从图3可见合金的真应力-真应变曲线可以分为3个阶段：第一阶段为加工硬化阶段，流变应力随变形量的增加呈比例增加；第二阶段为流变软化阶段，流变应力继续增大，达到临界应变时，动态再结晶发生导致其增速减缓，从而达到峰值应力，伴随着动态再结晶的持续发生，流变应力开始逐渐减小；第三阶段为稳态阶段，加工硬化与流变软化达到动态平衡，流变应力趋向于稳态。升高变形温度或者降低应变速率可促进动态再结晶发生，合金的流变应力有所减小；同时，随着变形温度降低和应变速率升高，流变应力稳态出现时间有所延迟。以上分析结果与文献[3，9，14-15]报道的镍基高温合金流变应力演化规律一致。

在热压缩实验过程中，试样与压头间的摩擦影响试样的对称变形，使用润滑剂和石墨箔也无法完全消除摩擦。本文利用EBRAHIMI 等[16]提出的摩擦修正模型修正实验采集的真应力-真应变曲线，如图3所示。从图3可以看出：修正后合金流变应力曲线的形态以及典型的特征位置均未发生改变，其变化趋势与修正前的相同；同时，经过修正后的曲线均位于实测曲线下方，流动应力摩擦修正值与实验值偏差在16%以内，在低温高应变速率下偏差稍大。这主要是由于摩擦力对接触面合金径向流动的限制改变了试样的单向应力状态，增大了变形抗力，在低温高应变速率下变形抗力更大。上述规律与TAN等[17]报道的一致。

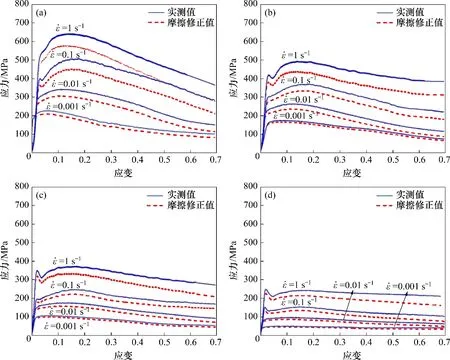
图3 热挤压-退火态Ni-Co-Cr基粉末高温合金摩擦修正前后的真应力-真应变曲线Fig.3 True stress-true strain curves of hot extruded-annealed Ni-Co-Cr-based PM superalloy before and after friction correction

2.2 本构关系方程的建立

SELLARS 等[11]提出的Arrhenius 方程被广泛用于建立合金热压缩变形流变应力σ与变形条件（应变速率˙、变形温度T）之间的关系。Arrhenius方程的3种表达式分别为：

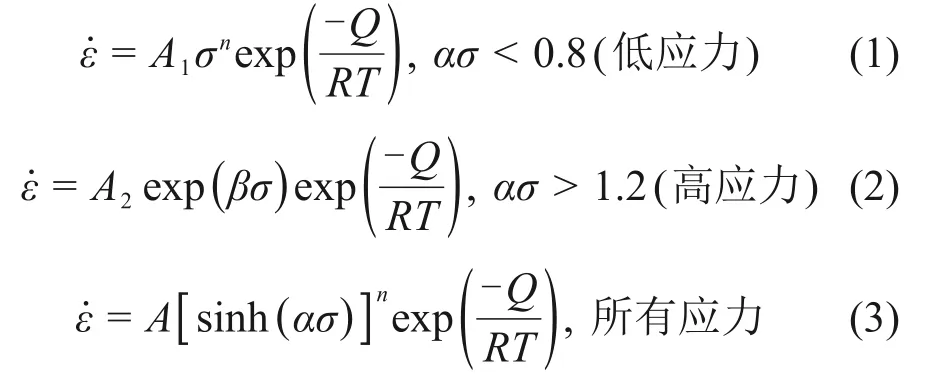
式中：Q为热变形激活能；R为摩尔气体常数；A1，A2，A，α，n和β均为材料常数，其中α=β/n。ZENER等[18]提出用Zener-Hollomon参数Z描述应变速率和变形温度对合金热变形的耦合作用，如下式所示：

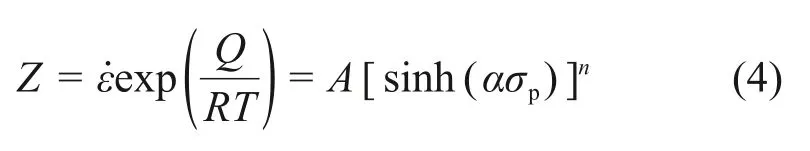
采用双曲正弦型公式（式（3））并结合式（4）构建热挤压-退火态Ni-Co-Cr基粉末高温合金的本构关系方程，对式（1），（2）和（3）两边取对数，将摩擦修正后的峰值应力（σp）代入式中并利用Origin 软件进行线性回归分析，所得各线性回归曲线如图4所示。结合线性回归分析结果和计算机反复迭代，求解得出方程中的各未知参数，对式（3）取对数后并进行微分，可得

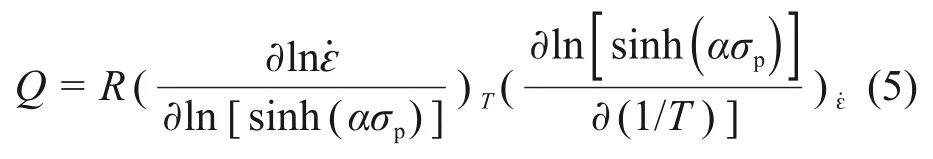
式（5）右边两项分别为一定温度下ln-ln[sinh（ασp）]关系曲线（图4（c））的斜率和特定应变速率下ln[sinh(ασp)-（1/T）曲线（图4（d））的斜率，从而可求出变形激活能Q，则可得以Z参数表示的合金的流变应力本构方程为

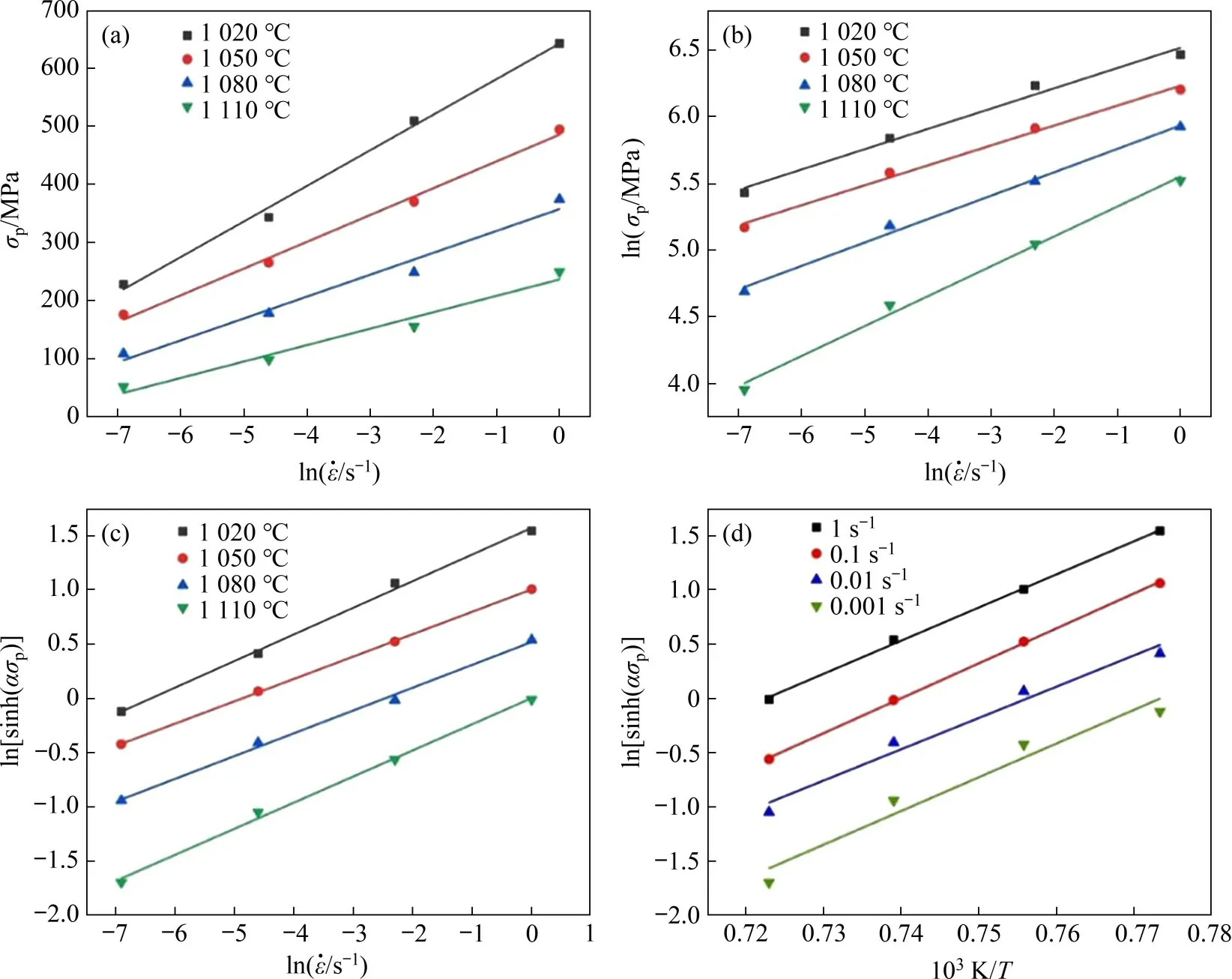
图4 热挤压-退火态Ni-Co-Cr基粉末高温合金热压缩峰值应力与应变速率和变形温度的关系Fig.4 Relationship between peak stress and strain rate or deformation temperature for hot compression of hot extruded-annealed Ni-Co-Cr-based PM superalloy

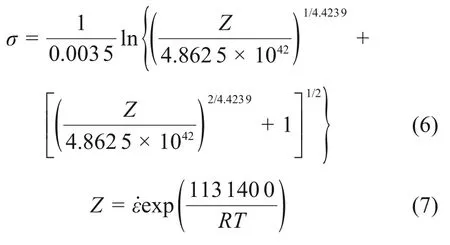
热挤压-退火态合金热挤压-退火态Ni-Co-Cr基粉末高温合金的热变形激活能Q为1 131 400 J/mol。

2.3 不同变形条件下的微观组织演变

热挤压-退火态Ni-Co-Cr基粉末高温合金在不同热压缩条件下试样中心区域的微观组织如图5所示。从图5可见：在低温或高应变速率下，原始晶粒的大角度晶界附近只生成少量动态再结晶晶粒；升高变形温度或者降低应变速率，动态再结晶晶粒的数量明显增加，这是因为温度升高或应变速率降低为合金中的原子扩散、位错滑移以及晶界迁移提供了更有利的条件；当应变速率为0.01 s-1、变形温度为1 020 ℃时，动态再结晶晶粒的质量分数较低；随着变形温度升高，合金中变形带的数量增加，位错滑移增强，动态再结晶程度有所增强；当变形温度达到1 080 ℃时，晶界处的动态再结晶晶粒数量进一步增加；当变形温度升高至1 110 ℃时，已生成的动态再结晶晶粒明显长大，晶粒粒径的不均匀性也显著提高。

图5 热挤压-退火态Ni-Co-Cr基粉末高温合金在不同变形条件下的金相组织Fig.5 Metallographic microstructures of hot extruded-annealed Ni-Co-Cr-based PM superalloy under different deformation conditions

2.4 动态再结晶模型的建立

2.4.1 临界应变模型

由于变形所导致的位错累积，动态再结晶一般在流变应力达到峰值应力前就开始发生。动态再结晶开始发生时所对应的应变称为临界应变（εc）。为了建立热挤压-退火态Ni-Co-Cr基粉末高温合金的动态再结晶模型，需要确定临界应变的表达式。本文利用加工硬化率（θ=dσ/dε）和真应力-真应变曲线，并结合经验公式获得实验合金临界应变公式。首先，对合金热压缩的真应力-真应变曲线进行多项式拟合，只拟合峰值应力前的曲线以提高曲线拟合精度。然后，对拟合曲线求导得到加工硬化率，如图6（a）所示，曲线拐点即为开始发生动态再结晶的临界点。对加工硬化率曲线继续求导从而确定曲线拐点，拐点对应的应力为临界应力，即可得到相对应的临界应变，如图6（b）所示。

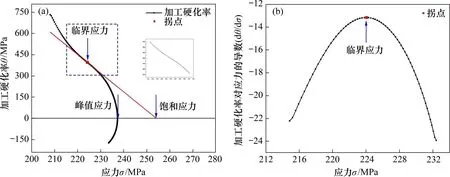
图6 热挤压-退火态Ni-Co-Cr基粉末高温合金热压缩变形θ-σ和dθ/dσ-σ关系曲线Fig.6 Relationships of θ versus σ and dθ/dσ versus σ for hot compression of hot extruded-annealed Ni-Co-Cr based PM superalloy

临界应变可用如下模型描述[19]：

式中：m1和a1均为材料常数。对式（7）两边同时取对数并进行线性拟合，结果如图7所示。据图7可得出m1=0.170 46，a1=3.347×10-6。故热挤压-退火态Ni-Co-Cr 基粉末高温合金热压缩临界应变模型为

图7 热挤压-退火态Ni-Co-Cr基粉末高温合金热压缩变形εc与参数Z的关系曲线Fig.7 Relationship between εc and Z for hot compression of hot extruded-annealed Ni-Co-Cr based PM superalloy

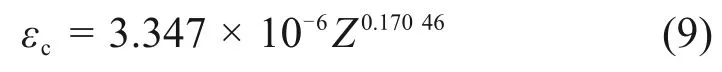
2.4.2 动态再结晶动力学模型

利用Avrami 公式建立Ni-Co-Cr 基粉末高温合金的动态再结晶体积分数（XDRX）模型[20]：

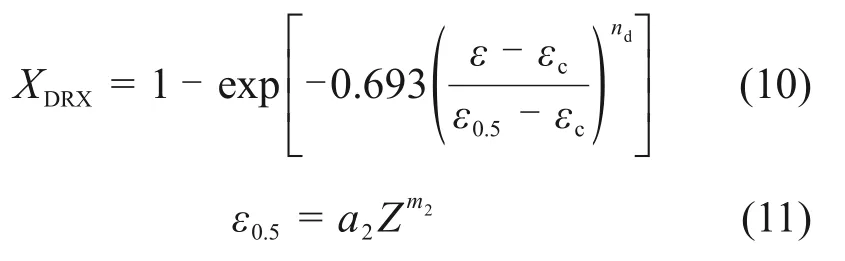
式中：nd为Avrami 常数；ε0.5为发生动态再结晶体积分数为50%时对应的应变[21]；a2和m2均为材料常数。

当ε≥εc时，流变应力σ与动态再结晶体积分数XDRX之间存在如下关系[22]：

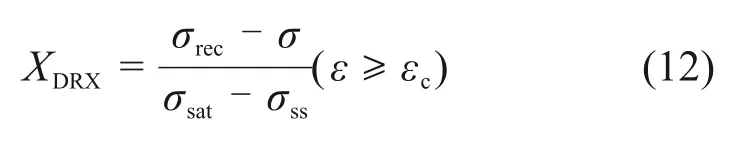
式中：σsat和σss分别为饱和应力和稳态应力；σrec为动态回复是合金主要软化机制时的应力。σsat，σss和σrec均可从真应力-真应变曲线中获得，由此可得到不同变形条件下的XDRX。

分别对式（10）和式（11）两边取对数，可得：

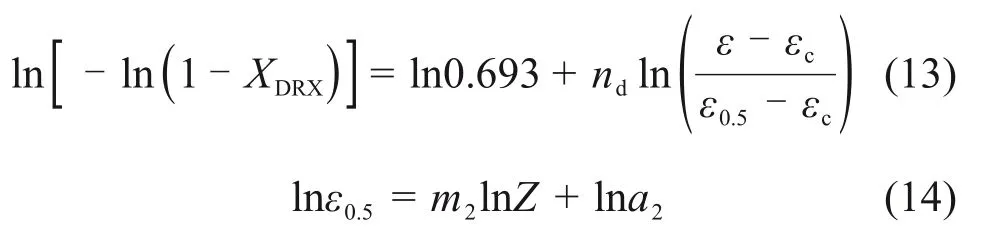
将已知参数分别代入式（12）和（13），经线性回归分析后可求得：a2=3.174×10-2，m2=0.022 53。热挤压-退火态Ni-Co-Cr基粉末高温合金热压缩变形ε0.5与参数Z之间的关系曲线如图8所示，热挤压-退火态Ni-Co-Cr 基粉末高温合金热压缩变形ln[-ln（1-XDRX）]-ln[（ε-εc）/（ε0.5-εc）]关系曲线如图9所示，可得nd=1.84。因此，热挤压-退火态Ni-Co-Cr基粉末高温合金动态再结晶动力学模型可表示为：

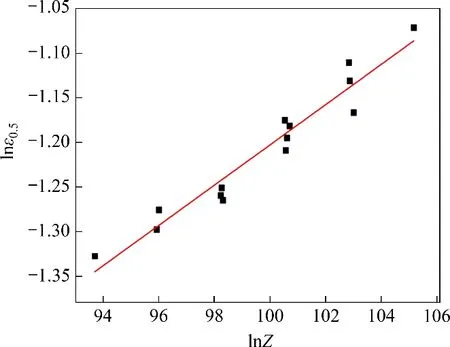
图8 热挤压-退火态Ni-Co-Cr基粉末高温合金热压缩变形ε0.5与参数Z关系曲线Fig.8 Relationship between ε0.5 and Z for hot compression of hot extruded-annealed Ni-Co-Cr based PM superalloy

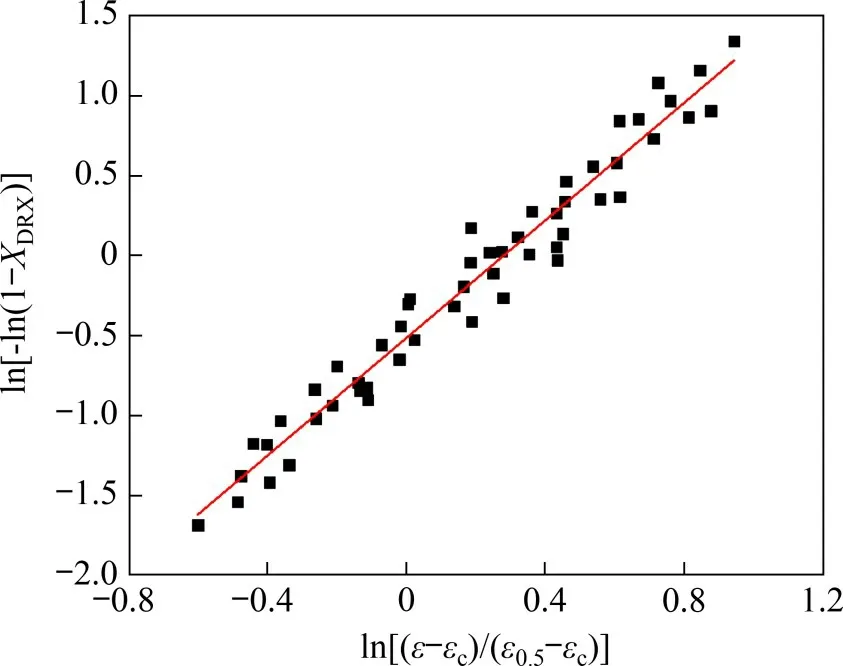
图9 热挤压-退火态Ni-Co-Cr基粉末高温合金热压缩变形ln[-ln（1-XDRX)]-ln[（ε-εc）/（ε0.5-εc）]关系曲线Fig.9 Relationship between ln[-ln（1-XDRX）]and ln[（ε-εc）/（ε0.5-εc）]for hot compression of hot extruded-annealed Ni-Co-Cr based PM superalloy

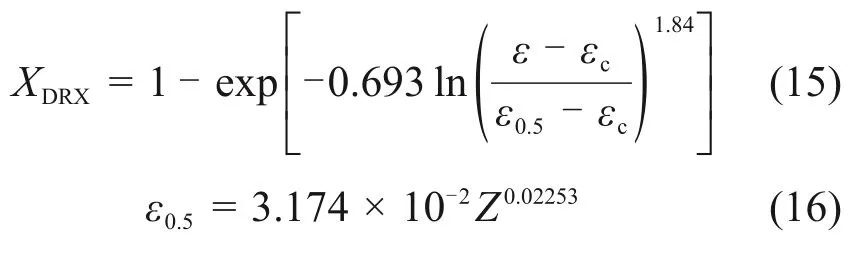
2.4.3 动态再结晶晶粒粒径模型

动态再结晶晶粒粒径模型一般可表示为[23]

式中：a3和m3均为材料常数。对式（16）两边取对数，将实验测得的不同变形条件下的动态再结晶晶粒粒径代入式（17）并进行线性回归分析，所得结果如图10所示。由图10可得动态再结晶晶粒粒径模型表达式为

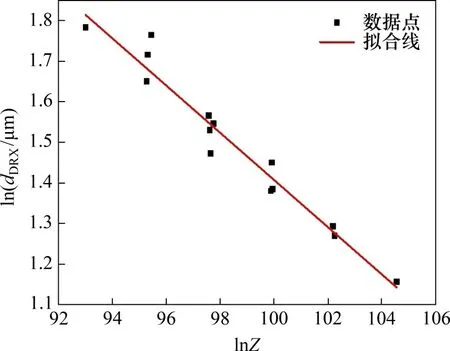
图10 热挤压-退火态Ni-Co-Cr基粉末高温合金热压缩变形参数Z与动态再结晶晶粒粒径dDRX的关系曲线Fig.10 Relationship between Z and dynamic recrystallized grain size dDRXfor hot compression of hot extruded-annealed Ni-Co-Cr based PM superalloy

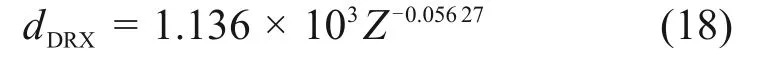
利用动态再结晶晶粒粒径模型（式（16））和动力学模型（式（9）），根据Waspaloy 合金热压缩过程的平均晶粒粒径（dave）模型[24]，得

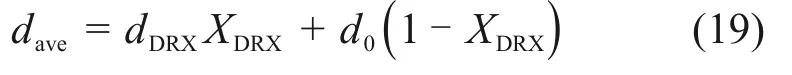
其中：d0为原始晶粒粒径，为10.21 μm。将求得的动态再结晶体积分数（XDRX）和动态再结晶晶粒粒径（dDRX）代入式（19），即可得dave。

2.5 有限元模拟结果及其验证

2.5.1 不同变形条件下的有效应变场分布模拟

热挤压-退火态Ni-Co-Cr 基粉末高温合金1/2圆柱试样在不同变形条件下的有效应变场模拟分布如图11所示。从图11可见：圆柱试样平均有效应变为0.67～0.69，与实验设定值（0.693）之间的相对误差为0.4%～3.0%；同时，不同变形条件下的有效应变分布云图表现出相似的分布不均匀性；有效应变沿试样径向中心线和轴线呈对称分布；试样剖面的最大有效应变位于中心位置，边缘鼓状区的次之，端面与模具接触的区域最小[24-25]。对比图11（a），（b）和（c）可见：在特定变形温度下，降低应变速率，试样剖面中心区域的最大有效应变有所增加。对比图11（c），（d）和（e）可知：在同一应变速率下，升高变形温度，最大有效应变也会增大。

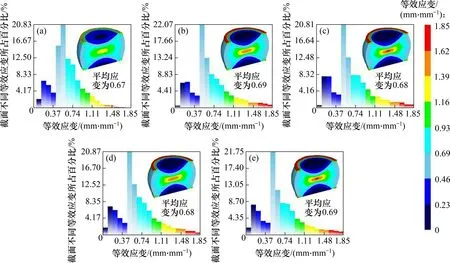
图11 热挤压-退火态Ni-Co-Cr基粉末高温合金1/2圆柱试样在不同变形条件下有效应变分布的模拟与预测Fig.11 Simulation and prediction of effcetive strain distribution on half of the hot extruded-annealed Ni-Co-Cr-based PM superalloy cylindrical specimen under different deformation conditions

2.5.2 不同变形条件下的动态再结晶组织模拟与验证

图12所示为不同变形条件下热挤压-退火态Ni-Co-Cr 基粉末高温合金1/2 圆柱试样动态再结晶体积分数分布云图。从图12可以看出：由于应变、应变速率以及变形温度的非线性耦合作用，动态再结晶体积分数的分布也是不均匀的，大部分区域发生了不完全动态再结晶；在试样剖面，边缘鼓状区和靠近端面的区域动态再结晶程度较低，中心区域由于产生的有效应变更大，故再结晶程度较高。从图12（a），（b）和（c）可见：在特定变形温度下，降低应变速率，试样剖面中心区域的动态再结晶体积分数明显增加。这主要是在高应变速率下，合金热变形时间较短，位错塞积产生应力集中，应力不能及时释放，从而抑制了动态再结晶的发生。从图12（c），（d）和（e）可见：变形温度升高为合金发生动态再结晶提供了更高的能量，故试样剖面中心区的动态再结晶体积分数也随之增大。微观组织演化趋势的的模拟结果与WU 等[4,10]所得模拟结果一致。

不同变形条件下合金1/2圆柱试样的平均晶粒粒径云图如图13所示。由图13可知：由于动态再结晶的发生引起了晶粒细化，而不同变形条件下试样发生动态再结晶的程度有所不同，故平均晶粒粒径分布也有所不同；试样剖面上的最小和最大平均晶粒粒径分别出现在中心区域和靠近端面的难变形区域。结合图12的分析结果可知，动态再结晶发生比例越大的区域，晶粒细化程度越高[24]，平均晶粒粒径越小。

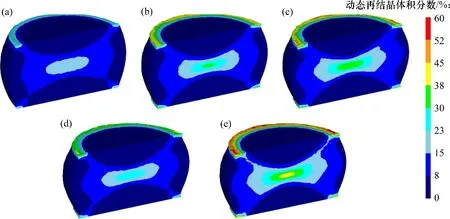
图12 热挤压-退火态Ni-Co-Cr基粉末高温合金1/2圆柱试样在不同变形条件下动态再结晶体积分数分布的模拟与预测Fig.12 Simulation and prediction of DRX volume fraction distribution on half of the hot extruded-annealed Ni-Co-Crbased PM superalloy cylindrical specimen under different deformation conditions

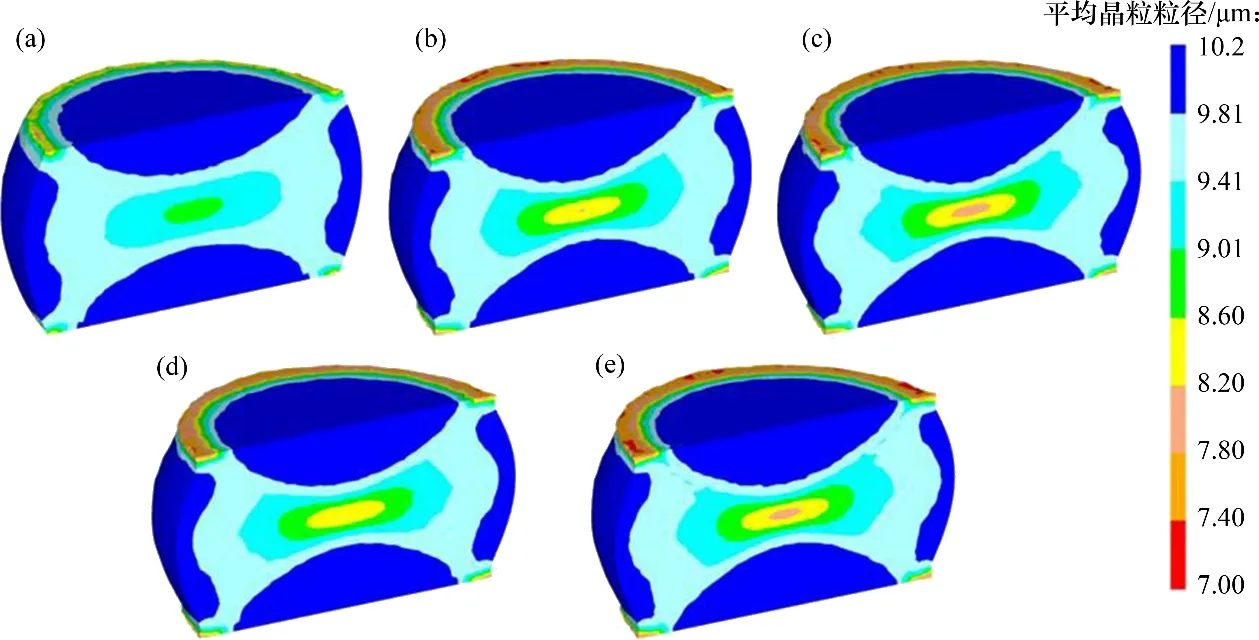
图13 热挤压-退火态Ni-Co-Cr基粉末高温合金1/2圆柱试样在不同变形条件下平均晶粒粒径分布的模拟与预测Fig.13 Simulation and prediction of average grain size distribution on half of the hot extruded-annealed Ni-Co-Cr-based PM superalloy cylindrical specimen under different deformation conditions

热挤压-退火态Ni-Co-Cr基粉末高温合金圆柱试样剖面中心区动态再结晶体积分数和平均晶粒粒径的模拟结果与实验结果对比如图14所示。从图14可见：动态再结晶体积分数和平均晶粒粒径的模拟值与实验值变化规律相似；动态再结晶体积分数的相对误差在4%～7%之间，平均晶粒粒径相对误差为4%左右，均较小，验证了构建的动态再结晶模型的正确性。经分析可知，热挤压-退火态合金中存在大量的γ'析出相（如图1（b）所示），而γ'相在合金的动态再结晶过程中起着不可忽视的作用[26]。然而，目前的Deform-3D软件尚未考虑析出相对动态再结晶过程影响的相关设置，导致模拟结果与实验结果之间仍然存在误差。

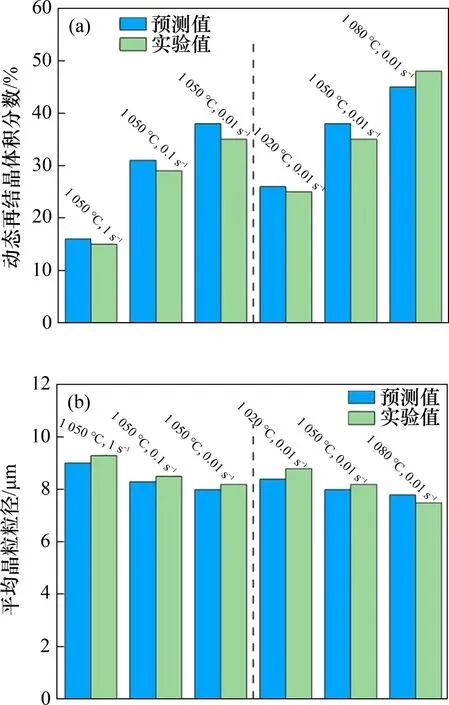
图14 实验结果与模拟结果对比Fig.14 Comparison between experimental results and FE simulated results

2.5.3 不同变形区域的宏观场及微观组织分布

为进一步分析热压缩过程中热挤压-退火态Ni-Co-Cr 基粉末高温合金的微观组织演变规律，以变形条件（温度为1 050 ℃、应变速率为0.1 s-1）的压缩试样为对象，沿其剖面的横向中心轴线选取具有代表性的3个区域进行进一步有限元模拟和微观组织分析，结果如图15所示（其中，P1处于大变形区，P3 位于自由变形区，P2 介于大变形区与自由变形区之间）。

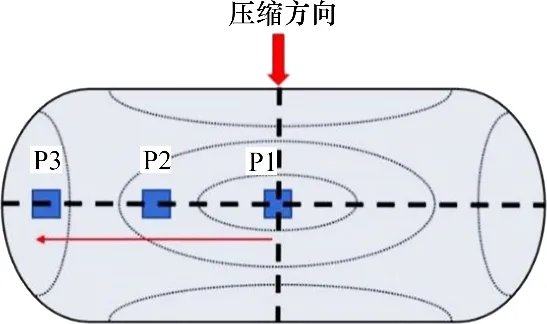
图15 变形试样剖面的典型区域Fig.15 Typical region on the longitudinal section of deformed specimen

图16所示为变形试样的应变、应变速率、应力及温度的分布与演化规律。从图16（a）可见：不同区域的有效应变均随着压缩量增加而增加[24]；P1区的有效应变最大，P2 区的次之，P3 区的最小。从图16（b）可见：沿横向中心线越靠近中心区域，应变速率越大，有效应变增加越快。除难变形区外，试样其他区域的应力分布比较均匀，应力曲线与实验曲线变化趋势相一致（图16（c））。试样内部的温度场分布整体较均匀，波动较小，中心区域温度略高于边缘区域温度，如图16（d）所示。

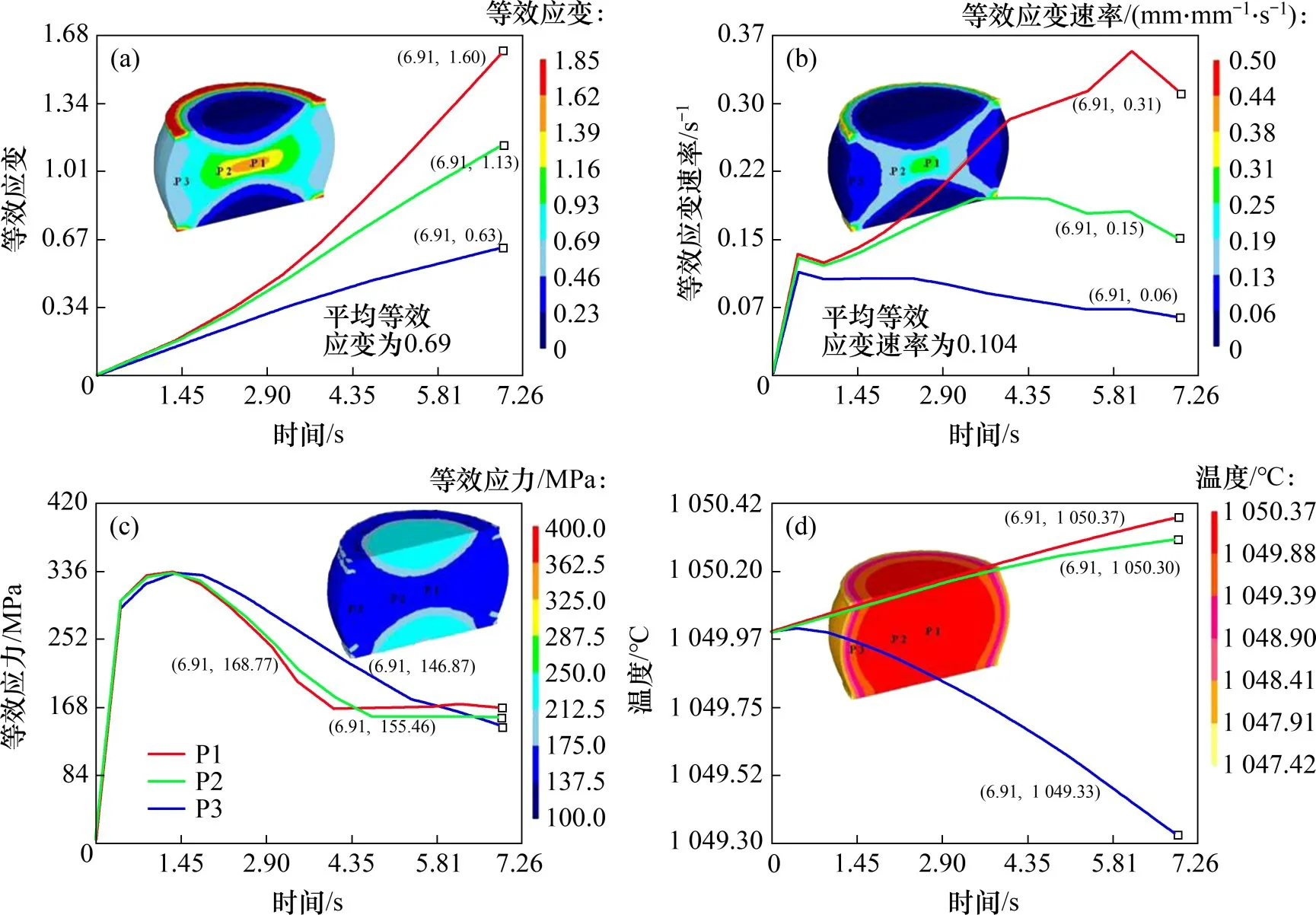
图16 热挤压-退火态Ni-Co-Cr基粉末高温合金1/2圆柱试样温度为在1 050 ℃、应变速率为0.1 s-1的变形条件下宏观场分布模拟预测Fig.16 Predicted distribution of macroscopic field on half of the hot extruded-annealed Ni-Co-Cr-based PM superalloy cylindrical specimen under deformation temperature of 1 050 ℃and strain rate of 0.1 s-1

为了验证在同一试样、不同区域的宏观场分布规律的正确性，对温度为1 050 ℃、应变速率为0.1 s-1条件下试样的3个典型区域进行EBSD表征，图17所示为变形试样不同区域微观组织的EBSD取向图。由图17可知：与原始显微组织（图1（a））相比，试样不同位置的晶粒形貌均发生了明显变化；P3 区由于变形量较小，晶界附近有少量细小的动态再结晶晶粒生成；随着变形量增大（P2区），晶粒的变形加剧，动态再结晶晶粒明显增多；中心区域P3 处由于变形量最大，有大量细小的动态再结晶晶粒生成。上述规律反映了圆柱试样在热变形过程中的不均匀性，验证了不同区域宏观场模拟的准确性；从边缘区域到中心区域，随着有效应变增加，动态再结晶晶粒数量明显增加，中心区域动态再结晶体积分数最高，越靠近中心区域的位置，其晶粒细化越明显。

图18所示为变形试样不同区域的KAM（kernel average misorientation）图，其中深色区域代表低KAM 值区，浅色区域为高KAM 值区。KAM 值越大，表明位错密度和变形储能越高，高的位错密度和变形储能有利于动态再结晶的发生和后续的晶粒生长[27]。在图17中发现不同区域的晶界处均有明显的锯齿状和凸起，从图18发现这些锯齿状晶界都伴有较大的KAM区域，这表明以晶界弓出为特征的不连续动态再结晶（DDRX）在这里可能被激活。在边缘区域（P3），沿着晶界或变形晶粒的内部只能观察到少量具有低KAM值的细晶粒；越靠近中心区域，在晶界周围清晰可见的低KAM值细晶粒越多，形成了典型的“项链”结构[28]。这说明动态再结晶的发生充分地释放了变形储能，新生成的DRX 晶粒内部位错密度较低，能量较小。综合图17和图18还可知，本文所研究的热挤压-退火态Ni-Co-Cr 基粉末高温合金的形核机制为不连续动态再结晶，在变形试样的不同区域均表现出不连续动态再结晶的典型特征。

图17 热挤压-退火态Ni-Co-Cr粉末高温合金圆柱试样剖面不同区域的EBSD取向图（温度为1 050 ℃、应变速率为0.1 s-1）Fig.17 EBSD orientation map in different areas of the longitudinal section of hot extruded-annealed Ni-Co-Cr-based PM superalloy cylindrical specimen under deformation temperature of 1 050 ℃and strain rate of 0.1 s-1

3 结论

1）热挤压-退火态Ni-Co-Cr基粉末高温合金热压缩流变应力曲线具有明显的动态再结晶软化特点；流变应力显示出对变形温度和应变速率的强烈敏感性，随着变形温度升高或应变速率降低，流变应力均有所减小。

2）热挤压-退火态Ni-Co-Cr基粉末高温合金热压缩变形的本构方程表达式为

3）结合热压缩实验数据和微观组织分析，建立的热挤压-退火态Ni-Co-Cr基粉末高温合金动态再结晶模型为

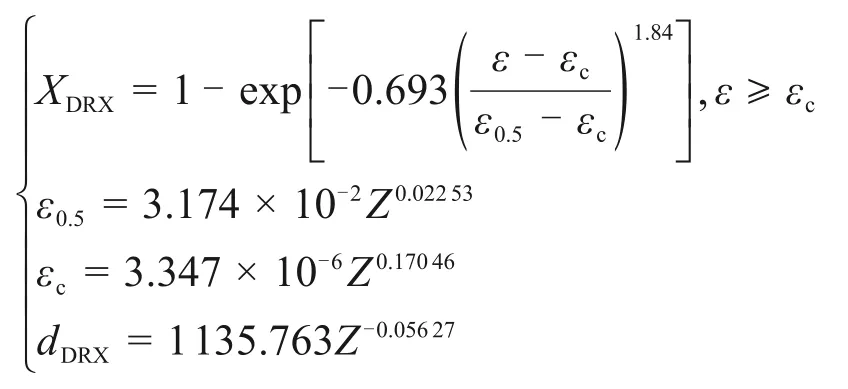
4）热挤压-退火态Ni-Co-Cr基粉末高温合金动态再结晶的主要形核机理是不连续动态再结晶；动态再结晶体积分数分布和平均晶粒粒径分布的有限元模拟结果与实验结果较吻合，证实所构建的动态再结晶模型可以预测热挤压-退火态Ni-Co-Cr 基粉末高温合金热压缩过程中的动态再结晶组织演变。