基于大数据和智能校园的大学生体质研究

罗 明

（江门职业技术学院，广东江门 529000）

大学生本身不愿意参加体育锻炼，而且学校对体育课程重视程度较低，课程设置不一致[1]，进一步加剧大学生体育锻炼不足[2]。因此，对高校大学生体质进行研究并获取适合的评价方法，具有十分重要的意义。

1 大学生体质现状

体质与健康密切相关[3]。身体健康以身体指标反映人体的健康状况。它已成为反映学生群体健康状况的一个特殊术语。目前，我国大学生的身体素质同步提高程度明显不足，学生肥胖和超重检出率继续上升。因为在我国高校体育教学中，仍然使用旧的、统一的成绩来评价和衡量大学生的身体素质，这使得体育课的教学内容十分僵化，教学过程更加单调。因此，它极大地阻碍了学生潜能的开发，也导致学生不重视、不喜欢、不积极参与学校体育课程。

2 建模分析

2.1 数据分类

本文采用SPSS 软件实现数据统计，再采用Logistic 线性回归模型完成拟合运算。同时，还增加了智能校园系统中关于学生骨骼发育、血氧指数和运动功能的数据指标，并发展和扩展为因子组，符号表如表1 所示。

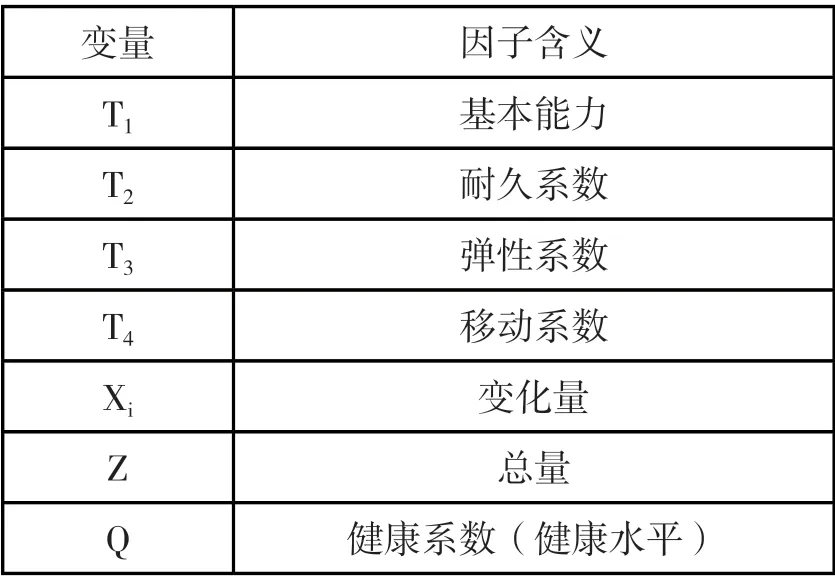
表1 符号表

为消除模型中的不确定性因素，补充测试对总体数据的影响被忽略。

2.2 模型建立

基于上述数据指标，可以开始模型解决方案。为了研究测试者的测试分数与身体状况之间的关系，首先对指标进行统一量化，然后将所有数据输入SPSS 软件。身高、体重得分和肺活量得分相加，如等式（1）所示：

在公式（1）中，XS 和XT 是指身高体重分数和肺活量分数，它们是基本能力因素的值。耐力、柔韧性和柔韧性项目都有很好的分数，可以直接使用。如果该系数包含多个变量，则应使用上述等式将变量分数组合成一个百分比系统。

有必要找出每个因素与学生体质之间的关系，并找出每个因素之间的权重值。输入SPSS 软件后，将T1～T4的KMO球面检验结果与球面检验相结合，得到总因子的方程（2）：

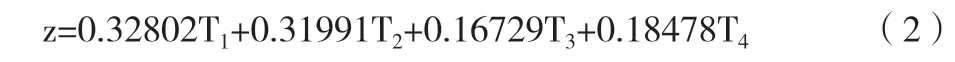
Logistic 线性回归模型中，模型相关变量为y，独立变量为xi。在m 个自变量的作用下，预期结果的条件概率为P=P（y=1 | x1，x2，x3…xn），则逻辑回归模型可表示为：

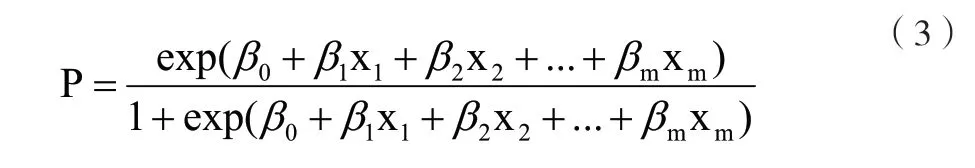
进而Sigmoid 函数可以由下式获得：

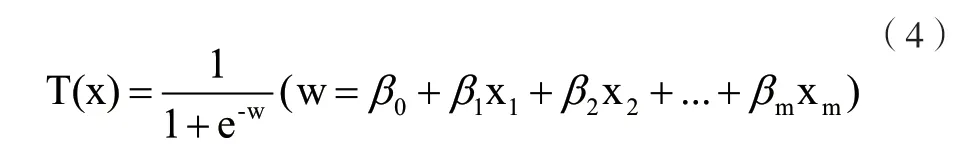
方程（4）的域为（-inf，+inf），取值范围为（0，1）。间接使用Sigmoid 函数，从而扩展了构建模型的内容。在函数中，由于参数范围为（0+∞) 这在函数所需的域中是非负的，通过SPSS 可知，每个数据的综合系数也是非负的。因此，对原始基本方程进行了改进，但由于加权后结果值随原始结果而变化，因此使用比例方程将综合因子z的结果控制在[0,10]，也就是说，方程中的所有子变量都与整体变化呈正相关。

建立逻辑模型，其中自变量T1、T2、T3和T4是每个子系数xij的矩阵。权重用于计算总因子z，公式如下：

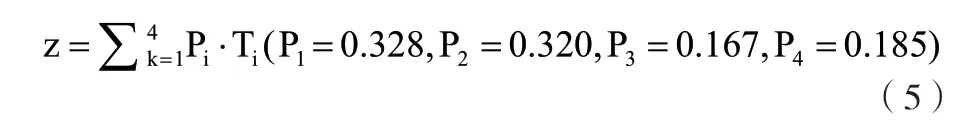
通过对替代模型的计算，得到了Q 和z 方程：

3 数据分析

将学生数据代入大数据进行计算。方程的域是z ∈（0,10），取值范围为Q∈（0,1）。方程采用Logistic 线性回归连续迭代计算，初始迭代次数为0.1。此处迭代系数分别设置为0.3、1.8 和2.5。当被测学生的所有因子均为0 时，学生的健康系数为0。随着自变量的增加，Logistic 模型得到的Q的增长曲线x 迅速上升。使用Matlab 绘制生长曲线图像，如图1 所示；以评价等级为0-5，分数值的分布区间如图2 所示；当评价等级为15-25 时，分数值的分布区间如图3 所示。

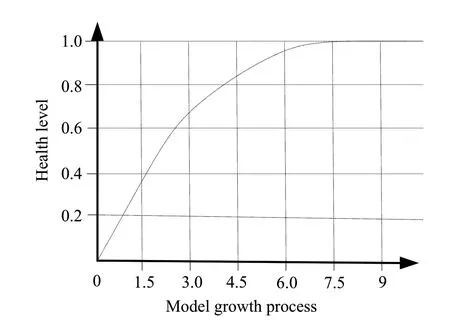
图1 增长曲线

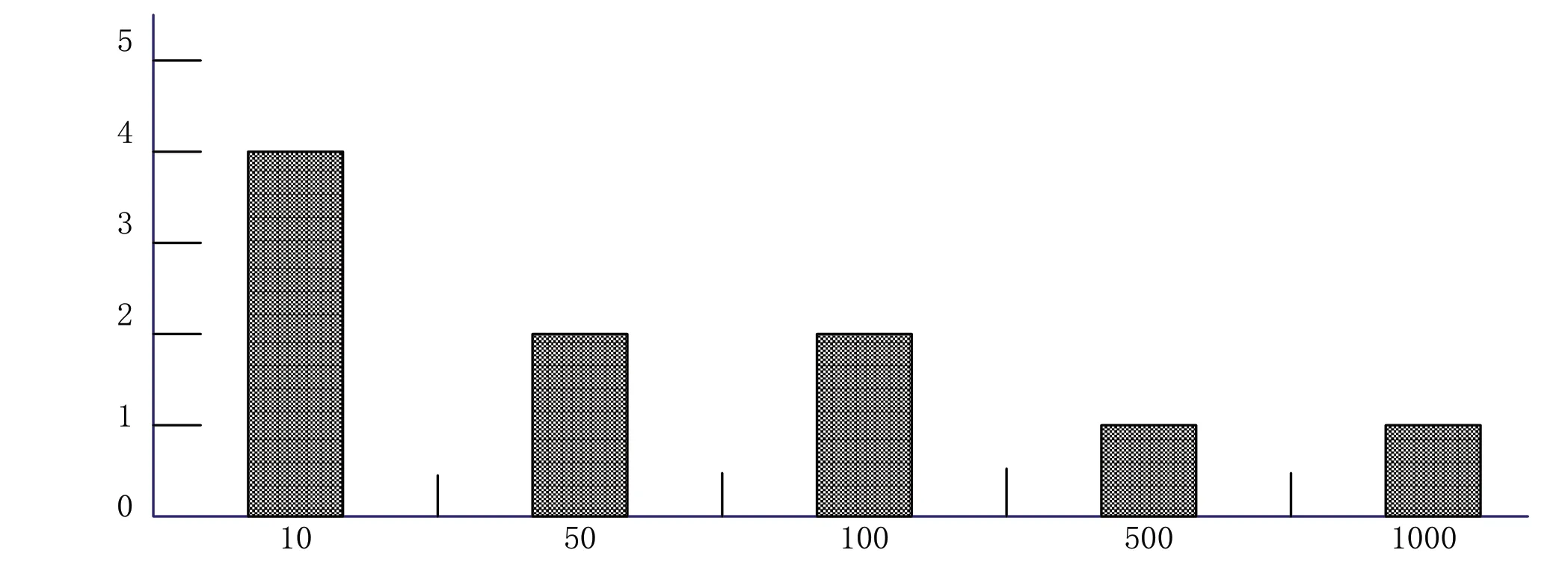
图2 评价等级为0-5 下的分数分布状况

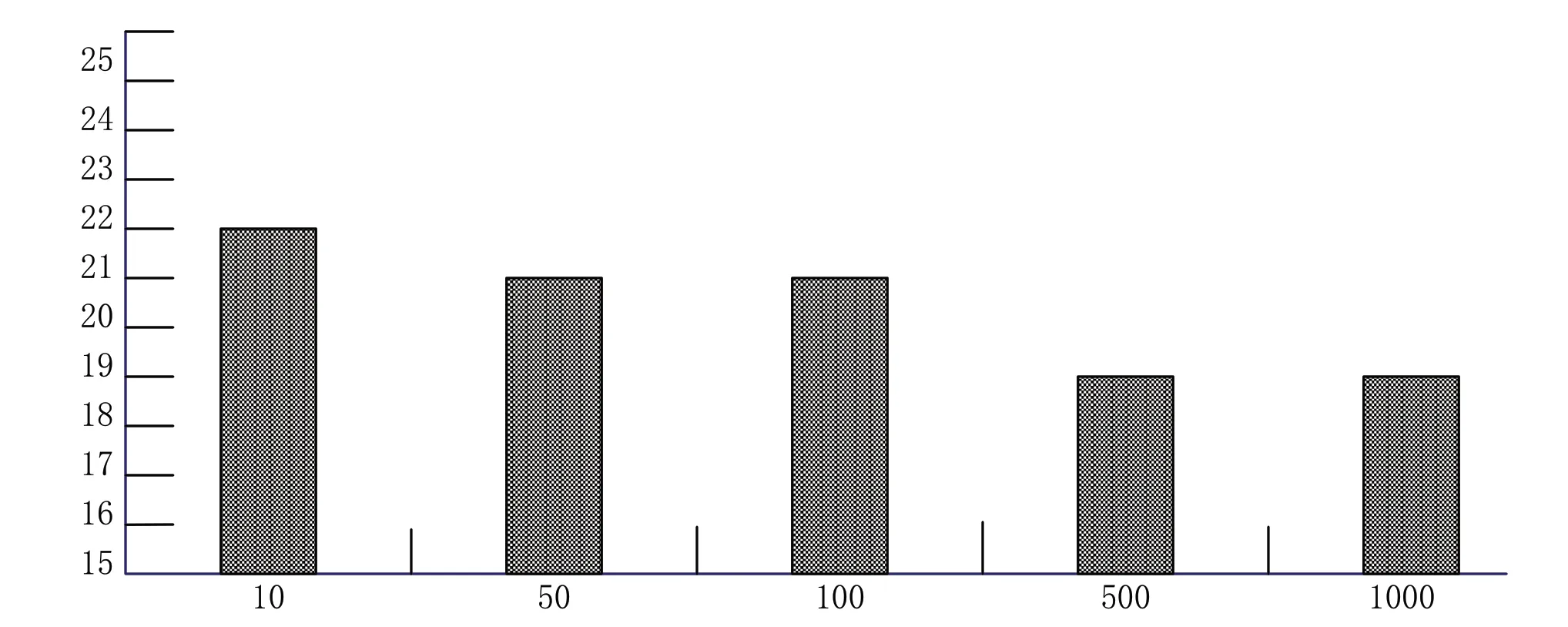
图3 评价等级为15-25 下的分数分布状况

4 结论

基于大数据的学生数据测量模型反映了学生的健康状况。结合智能校园系统的数据指标，可以得出结论，即当分数处于大多数人的水平时，学生的健康状况很可能是正常的。如果综合得分略低于多数，可针对学生得分较低的情况予以强调，导师应促进相应的锻炼，以预防健康风险。当总分远低于大多数学生时，应引起学校的注意。应跟踪学生的健康状况，并提供指导，提升大学生体质健康的整体水平。