基于聚类分类算法的IGBT健康状态分类研究

王志远， 孙鹏菊， 王海波， 杨舒萌

(输配电装备及系统安全与新技术国家重点实验室(重庆大学)， 重庆 400044)

1 引言

近年来，随着新能源技术的发展和进步，功率器件在各个领域得到了广泛的运用，尤其在轨道交通、工业自动化、新能源发电等领域所占比例越来越高[1-3]。绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)具有驱动简单、电压等级高、开关频率高等优点，常被作为功率变流器的核心器件[4]。由于IGBT模块老化过程缓慢[5]，如果不及时监测并评估模块当前的健康状态，会对系统的稳定性造成极大的影响，甚至导致灾难性事故发生[6-8]。因此，IGBT模块的健康状态评估影响到功率装置系统的稳定性，对整个电力系统安全稳定、高效经济地运行具有深远的意义。

日新月异的计算机技术丰富了IGBT模块健康状态评估的手段[9,10]。大量研究表明，IGBT模块老化会对外部电气参数产生影响，所以监测外部电气参数变化是评估模块健康状态的重要手段[11,12]。由于模块电气参数变化不明显，采用合适的算法处理模块老化特征量数据尤为重要。因此，如果选择合适的算法手段，分析IGBT模块老化特征量数据，划分模块健康状态类别，并及时更换疲劳老化的功率器件，将极大地提高系统可靠性。

由于IGBT模块老化过程难以直接观测，因此需要分析老化过程中相关参数的变化情况，评估模块当前的健康水平。文献[13]对IGBT模块进行有限元仿真，分析每次功率循环条件下IGBT模块键合线的裂纹率，从而评估IGBT模块的健康状态。由于IGBT模块键合线健康情况和实际工况有关，因此该方法在实际应用中具有一定的局限性。文献[14]发现在特定门极驱动电压下，结温对短路电流的影响几乎可以忽略，因此可以通过监测短路电流的变化情况来判断当前IGBT模块是否失效。文献[15]分析了饱和压降随功率循环次数增多的变化趋势，从而得到器件失效时饱和压降的阈值。文献[16]通过分析数据手册发现，IGBT饱和压降在不同负载电流下温度特性不同，因此在饱和压降正负温敏系数交叉点的电流下进行测量，排除了温度的影响。文献[17]综合考虑了IGBT芯片结温、模块老化程度、集电极电流与饱和压降的关系，采用剪断键合线模拟老化的方式，发现在集电极电流和芯片结温相同时，IGBT模块的饱和压降随老化程度加深逐渐增加。文献[18，19]研究分析了多芯片IGBT模块的门极电压电流信号反映键合线断裂的情况，发现部分键合线的断裂并不会使门极开通电压信号和电流信号有明显的变化，只有当某个芯片失效后，门极电压和门极电流信号有明显的变化。以上文献通过特征量阈值方法只能判断模块是否失效，当模块正常工作时，无法准确评估当前模块所处的健康水平。文献[20]对IGBT模块所处外部环境条件进行了详细分析，基于蒙特卡洛算法计算寿命模型与环境因素的关系。该方法算法繁琐，实验周期长，且实际工况下环境条件复杂，可能会产生较大误差。文献[21]分析IGBT模块结温和剩余寿命的关系，通过实验数据拟合寿命模型参数，并通过数据驱动算法评估IGBT模块的健康状态。该方法准确度较高，但是对实验设备要求较高，需要采集到精确的结温值。以上文献通过一定的数据处理手段得到了模块寿命模型，但是方法复杂，并且模型的准确度受测量精度的影响较大，因此，分析IGBT模块的特征量变化情况，判断IGBT模块当前所处的健康状态，才能对系统起到有效预警作用，提高系统可靠性。

本文建立了一种基于聚类分类算法的IGBT模块健康状态分类评估模型。首先简述了聚类分类算法原理，并基于算法原理分析了健康状态分类评估模型的搭建过程；然后搭建IGBT模块老化测试平台，通过模拟老化的方式获取特征量数据；最后基于实验数据建立了IGBT模块的健康状态分类评估模型，并验证了评估模型的正确性。

2 聚类分类算法原理

为了减小单一特征量评价模块健康状态的误差，可以结合多个特征量的变化情况来综合判断IGBT的健康状态。根据特征量的变化过程，本文首先基于K-Means聚类算法将模块的健康状态划分为多个区间，然后基于支持向量机(Support Vector Machine,SVM)分类算法计算出划分模块健康状态的曲线方程，实现IGBT模块健康状态分类。

2.1 IGBT健康状态分类

由于IGBT模块老化过程难以直接观测，因此需要分析老化过程中相关参数的变化情况，评估模块当前的健康水平。对于IGBT模块的可靠性评估方法可以总结为基于失效状态判断的可靠性评估、基于可靠性评估手册的可靠性评估、基于寿命模型的可靠性评估三种方法。

基于失效状态判断的可靠性评估是一种直接的可靠性评估方法。该方法通常以某一种特征量为参考对象，分析模块失效时特征量的变化情况，并以此为标准判断IGBT的健康状态；可靠性评估手册是一些国家或者企业根据统计的故障数据和可靠性实验结果而制定的可靠性评估方法，基于已有的可靠性评估手册可以直接计算出器件在稳定运行期的故障率；基于寿命模型的可靠性评估方法从模块的失效机理出发，分析模块老化原理，建立模块的物理模型，并研究物理模型与电气参数的关系，从而建立模块的寿命模型。然后通过实验拟合分析模块寿命模型参数，实现模块的寿命预测，进而对模块可靠性进行评估。

本文为了简洁高效地判断IGBT模块所处的健康状态，在第一种方法的基础上进行改进，通过分析多个特征量的变化过程，基于聚类分类算法对模块当前所处的健康水平进行分析，一方面解决了单一特征量失效判断时无法评测当前模块健康水平的缺陷，另一方面避免了计算寿命模型，简化了计算过程，保证了系统稳定性。

2.2 聚类分类算法原理及实现

在K-Means聚类算法中，对于给定样本集D={x1,x2,…,xm}，基于最小化平方误差[22]原理，可以将样本集划分为C={C1,C2,…,Ck}，其中，xi(i=1,2,…,m)为第i个样本的特征量；Ck为第k个样本簇。样本簇划分原理如下：

(1)

式中，Eijl为经过j次迭代后，第i个样本特征量与第l(l=1,2,…,k)个样本簇中心的距离；μl为簇Cl的均值向量。直观来看，式(1)可以理解为簇中心到样本的距离。因此，基于K-Means聚类算法的思想，当健康状态区间为lmax时，各个健康状态样本与健康状态中心的距离可以写成：

(2)

式中，kmax为特征量的种类数；Mik为第i个健康状态样本对应的第k个特征量的参数值；Nljk为经过j次迭代后，第l个健康状态中心对应的第k个特征量参数值。

对于最小化问题，本文依据贪心策略求解，流程如图1所示。根据图1流程，基于聚类中心不再变化的准则，通过迭代优化的方法，计算出聚类中心，同时标记样本所属类别。在IGBT模块健康状态分类时，可以依据这样的方法计算IGBT模块的健康状态中心，并标记健康状态样本所属的健康状态区间。

图1 聚类算法流程

根据上述分析得到的IGBT模块健康状态类别，本文通过SVM算法进一步计算不同类别之间的分界面方程。由于IGBT器件的健康状态随着老化过程缓慢变化，需要对两两相邻的健康状态区间进行划分，因此本文将多分类SVM问题转化为相邻健康状态区间的二分类SVM问题。

对于相邻健康状态区间的样本集G={(x1,y1),(x2,y2),…,(xm,ym)}，其中，yi∈{-1,+1}为样本标签，表示属于不同的健康状态类别。根据SVM算法原理[23]，线性SVM模型如下：

(3)

式中，ω为分界面方程法向量；b为分界面方程位移项；E为惩罚因子；ξi为松弛变量。为了简化求解模型，引入拉格朗日乘子，将问题转换为二次规划问题后，本文采用了序列最小优化(Sequential Minimal Optimization,SMO)算法[23]进行求解，得到最优解后即可得到分界面函数如下所示：

(4)

式中，αi*、b*为分界面函数系数，由模型计算得出；κ(x,xi)为选取的SVM核函数；x为待测健康状态样本整体特征向量。综合以上步骤，首先根据K-Means聚类算法，对表征IGBT模块的健康状态的特征量进行处理，得到多个健康状态区间；然后基于SVM分类算法，计算相邻健康状态区间的分界函数；最后将待测样本代入分界函数中，评估当前模块的健康状态。

3 实验结果与分析

3.1 IGBT器件的短路电流特性

本文以英飞凌FF75R12RT4型号的IGBT模块为研究对象。图2中，每块IGBT开关的芯片由4根键合线并联连接到铜基板，Rw1、Rw2、Rw3、Rw4、Lw1、Lw2、Lw3、Lw4分别为每根键合线的等效电阻和电感，可以将4根并联键合线上的电阻电感等效为Rw和Lw。因此，可以得到IGBT模块内部等效电路图如图3所示，RG、LG为门极寄生电阻和电感；Re、Le为辅助发射极寄生电阻和电感；RE、LE为发射极寄生电阻和电感；iG为门极驱动电流；ISC为短路电流；VG为门极驱动电压；vge为IGBT模块的芯片级栅极-发射极电压。

图2 IGBT模块内部键合线电阻等效

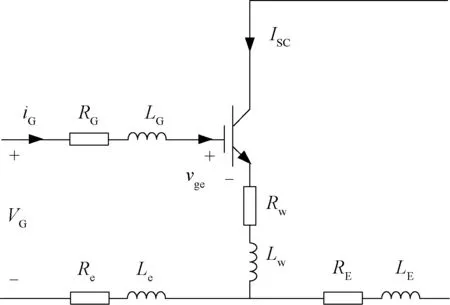
图3 IGBT模块内部等效电路图

当短路情况发生时，在门极所在的回路中建立基尔霍夫电压方程并化简，可以得到短路电流表达式如下：

(5)

式中，COX为氧化层电容；z为沟道宽度；LCH为沟道长度；μni为电子迁移率；αPNP为PNP晶体管的共基极放大倍数；VTH为门极阈值电压。从式(5)可知，IGBT模块稳态情况下的短路电流不仅受芯片自身结构的影响，同时封装结构中键合线的等效电阻也对其有影响作用。IGBT模块在工作过程中会发生性能退化，键合线产生裂纹等老化现象使得寄生参数Rw变化。由此可知，根据IGBT短路电流ISC的变化，可以对IGBT模块的状态进行评估。

图4为该模块的传输特性曲线，给出的是IGBT模块工作在电流饱和状态时(短路情况)驱动电压与集电极电流的关系。根据传输特性曲线可知，IGBT模块在不同门极驱动电压下对应不同的短路电流值。在相同的芯片结温Tj时，IGBT的短路电流随门极驱动电压VG的增加而增大。VGT是不同温度下传输特性曲线的交点，当门极驱动电压VGVGT时，IGBT模块的短路电流随芯片结温Tj的增加而减小。而在门极驱动电压VG约为9.2 V时，温度从25 ℃变化到150 ℃，IGBT模块的短路电流ISC基本不变。由此可知，在此交叉点对应的驱动电压下，短路电流不受芯片结温的影响。因此本文选取该驱动电压下的短路电流ISCT作为本次实验的老化特征量之一，依据老化过程中特征量的变化情况，基于聚类分类算法，划分IGBT器件的健康状态区间并确定分界函数。

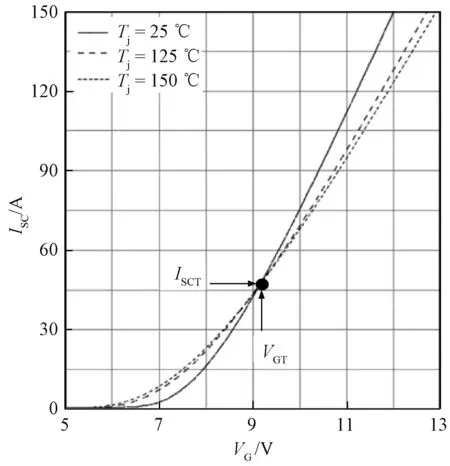
图4 IGBT模块传输特性曲线

3.2 IGBT器件的饱和压降特性

IGBT模块的老化失效形式主要有键合线脱落和焊料层疲劳两种，每一种对集射极饱和压降都有相应的影响，而且在 IGBT 模块正常运行情况下，这两种老化失效互相影响和促进。

图5为IGBT器件截面图。文献[24]对饱和压降进行分析，发现通态情况下的集-射极饱和压降VCE由P-i-N二极管部分的导通压降与MOSFET部分的导通压降共同决定，即:

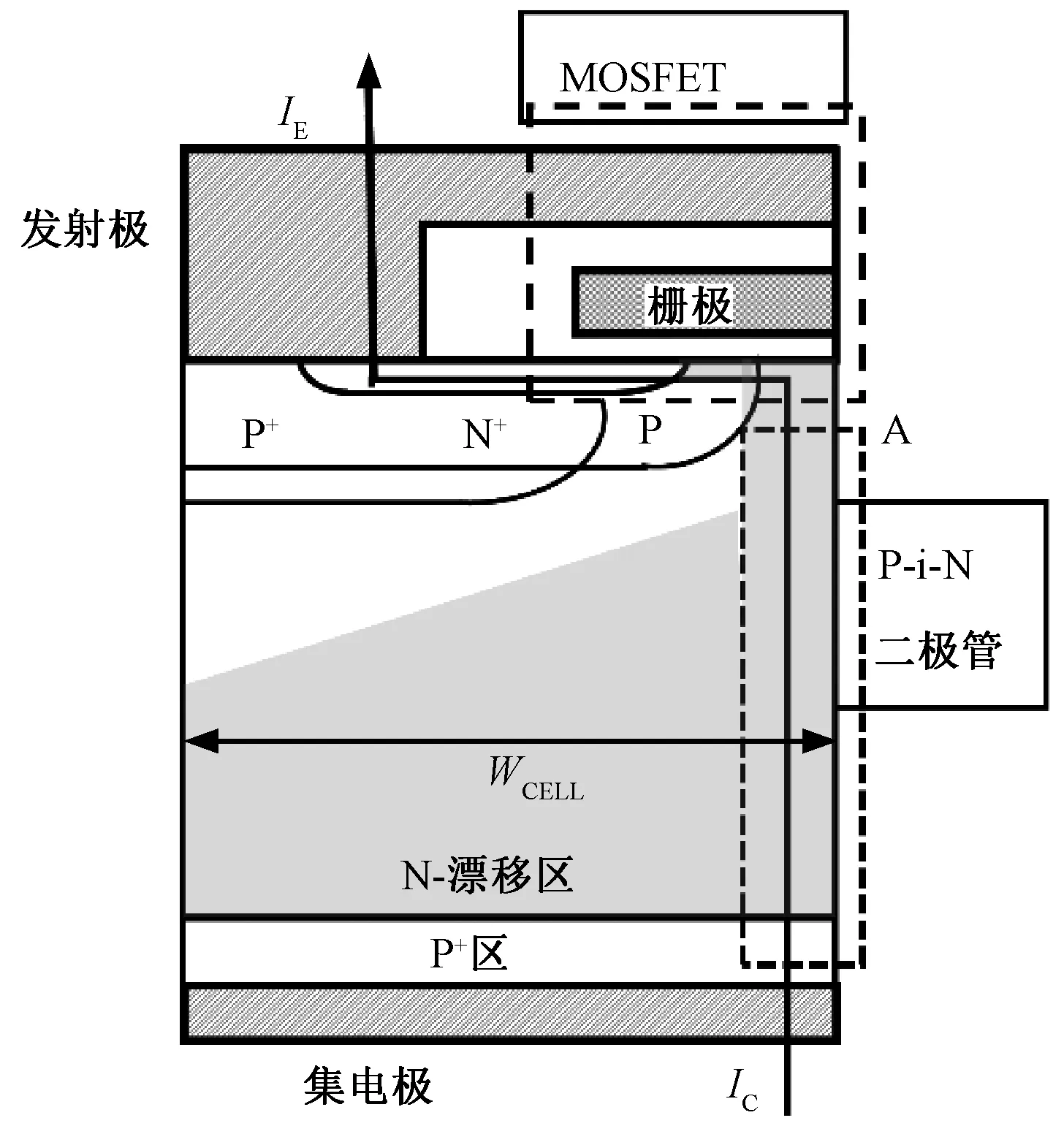
图5 IGBT器件截面图

(6)

式中，kB为玻尔兹曼常数；q为电子电荷；T为绝对温度；JC为电流密度；La为双极扩散长度；p为元胞尺寸；WN为N-基区宽度；F为扩散系数；Da为双极性扩散系数；ni为本征载流子浓度。从式(6)中可以看出，IGBT 模块饱和压降受到集电极电流、芯片结温、栅极驱动电压等因素的影响。文献[25]中发现封装模块的集射极饱和压降可以视为内部芯片的导通压降和连接部分的等效电阻的压降之和。因此，在器件正常工作中，随着器件老化，当键合线脱落时，键合线的等效电阻增加，导致集电极到发射极间的等效电阻增加。饱和压降也会产生相应变化；当焊料层老化时，内部热阻也会相应增大，导致内部结温升高，饱和压降随之增大。因此，饱和压降可以有效反映器件的健康状态。

3.3 实验原理

饱和压降测试电路如图6所示。由于IGBT模块功率等级为75 A，从安全考虑需要降额运行，因此采用50 A恒流源，环境温度20 ℃。实验过程中，设置IGBT导通控制时间5 ms，流过IGBT模块的电流大小约等于恒流源设置的输出电流。

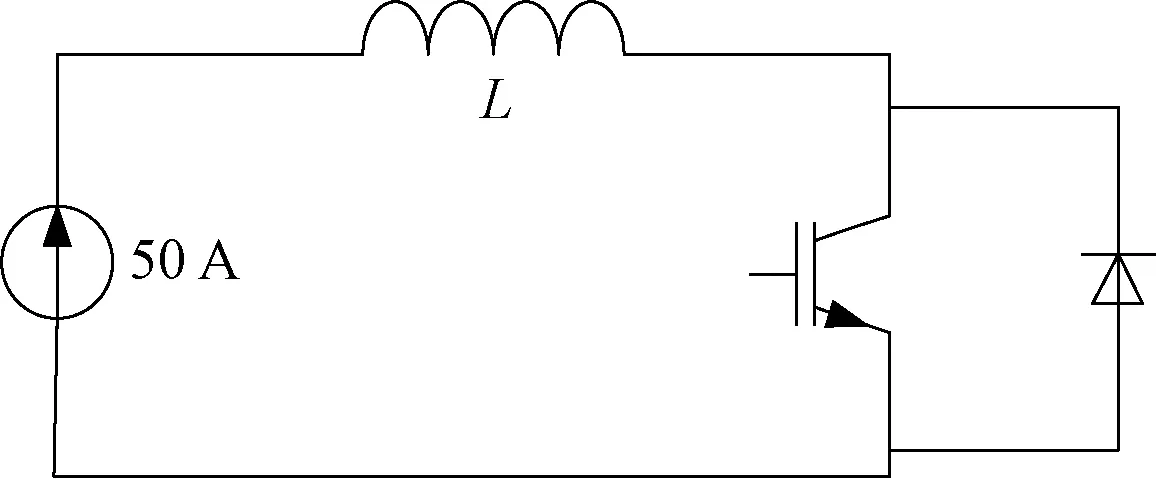
图6 饱和压降测试电路

短路电流测试电路如图7所示。稳压源输出电压100 V，环境温度20 ℃。实验过程中，由于IGBT模块短路安全工作区的限制，设置IGBT短路导通时间4 μs，驱动电压9.2 V。稳压源经过电阻R对储能电容C充电，当控制信号给IGBT模块触发脉冲时，电解电容C、回路电感L和IGBT模块形成闭合回路，使IGBT短路。

图7 短路电流测试电路

为了简化实验过程，本文采用人为剪断键合线的方式模拟器件老化。图8为IGBT模块开封后单个芯片的键合线连接图。图8中，模块栅极位于芯片中央，且通过一根键合线与铜基板相连；发射极有源区通过一层铝基板被均匀分成四个部分，共有8根键合线均匀分布，保证电流垂直流通。

图8 IGBT芯片顶视图

根据文献[26]所建立的发射极等效电阻网络仿真模型，可以发现，随着模块老化程度加深，不同位置键合线受到的电流应力不同，其中随着键合线断开数量的增多，铝基板和铜基板之间的键合线承受的电流应力比铝基板之间的电流应力大。

因此，为了使键合线模拟老化更符合实际情况，需要考虑剪断键合线的位置和次序。首先对每块铝基板和键合线进行了编号如图8所示，其中，a、b、c、d分别表示4块铝基板，铝基板与铜基板连接的左边第一根键合线编号起始为1。考虑到键合线位置的对称性，同时确保样本的充分性，本文设计了多种剪线方式见表1。

表1 模拟老化方式

3.4 实验结果与验证

在模拟老化方式1下，短路电流波形和饱和压降波形如图9和图10所示。图9中，曲线从上到下依次是剪断0到7根键合线的短路电流波形图，图10中，曲线从上到下依次是剪断7到0根键合线的饱和压降波形图。通过多次测试和分析实验波形后，选取t=3 μs时刻的短路电流值作为稳态短路电流；选取t=4.5 ms时刻的饱和压降值作为稳态饱和压降。表2表示随着键合线剪断根数增多，短路电流和饱和压降的变化情况。

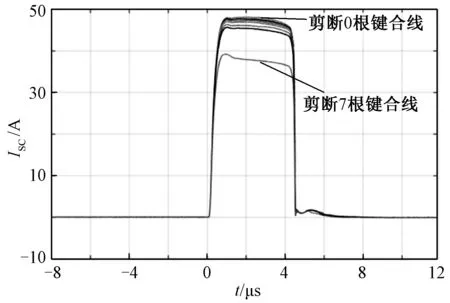
图9 短路电流波形图

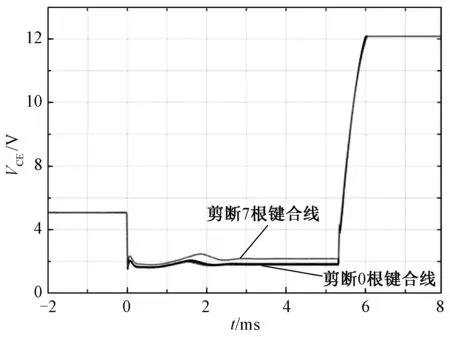
图10 饱和压降波形图

表2 模拟老化方式1下的特征量值

通过表2中数据的情况可以看出，随着老化程度的加深，短路电流和饱和压降均会上升，并且在老化后期变化显著，验证了短路电流和饱和压降作为老化特征量的有效性。同理可以监测其他模拟老化方式下的IGBT模块状态，采集特征量变化数据。

基于聚类分类模型，本文以样本特征量为输入，首先经过K-Means算法计算后，得到每个区间的聚类中心，结果如图11所示。其中为了降低不同模块之间生产工艺差异所造成的误差，本文以短路电流和饱和压降的偏差百分比作为老化特征量进行分析。

图11 聚类结果图

图11中，根据样本点到健康状态中心的距离，IGBT模块的健康状态大致可以划分为3个区间，分别表示模块健康期，故障预警期和模块失效期。图11中可以看出，IGBT模块健康状态样本在健康期较密集，而预警期和失效期的分界面并不明显，因此为了得到更准确的健康状态区间分界面函数，将样本特征量代入到式(4)中，计算分界面函数系数，结果如图12所示。

图12 分类结果图

图12中，IGBT模块的健康水平被准确划分为3个部分。从而得到以短路电流和饱和压降为特征量的聚类分类评估模型。基于该模型对IGBT特征量数据进行分析，即可得到IGBT模块的健康水平。

为了验证评估模型的有效性，本文以模拟老化方式2的特征量数据作为验证集，对健康状态分类评估模型进行了验证。结果如图13所示，并标出了检验样本的分布情况。

图13 检验样本分布图

图13中，根据验证集的样本分布情况可以判断模块所处的健康状态。根据分析结果可以看出，由于剪线次数的不同，IGBT模块的健康状态水平分别处于健康期、预警期和失效期，该评估结果与文献[27]的分析结果一致，验证了本文所提健康状态分类评估模型的正确性。

4 结论

本文以IGBT模块健康状态分类为目标，采用模拟老化的手段，获取IGBT模块的健康状态数据，同时采用聚类分类算法建立了健康状态分类评估模型，实验结果表明所建模型能对IGBT健康状态进行分类评估，为实现功率器件的状态监测提供了技术支撑。主要结论如下：

(1) 选取短路电流和饱和压降为老化特征量，通过人为剪线的方式模拟器件老化，分析了老化特征量的变化趋势。

(2) 基于聚类分类算法，划分模块健康状态区间，计算区间分界面方程，建立了IGBT模块的健康状态分类评估模型，并进行了实验验证，所建模型分类结果与文献中失效判别结果一致，验证了模型的正确性。