数学多选题的基本类型及破解策略
林菊芳
(湖北省黄冈市团风中学 438800)
数学多项选择题是选择题的一种,它具有备选答案不唯一,存在多个正确选项的特点.试题可以从多角度审视某一核心数学概念的全貌,考查更多的数学基本知识点或能力点,对学生有较好的区分度.解答此类型数学多项选择题可以用直接法、特值法、反证法、数形结合法等逐项判断.
一、数学多选题的基本类型
数学多项选择题根据各选择支干扰因素的区分,对应的选项设计大致分为以下六种基本类型,即:
(1)条件疏漏:将一些数学问题中容易疏漏的条件所产生的结果设计为选择支干扰项;
(2)实际背景忽视:细心模拟学生的演算过失和差错,得到迷惑性较强的选择支干扰项,对提高试题的针对性和鉴别力十分有效;
(3)概念混淆:针对学生容易混淆的数学相关概念、性质等设计选择支干扰项;
(4)题意误解:读题不慎,审题不细,误解题意,由此引发的错误结论设计为选择支干扰项;
(5)推理错乱:由不合逻辑的推理而造成的错误结果设计为选择支干扰项;
(6)思维定势:熟悉的内容,相似的形式,常会令人产生类比与联想,可能产生负迁移,由此导致的错误设计为选择支干扰项等.
二、数学多选题的破解策略
1.概念辨析类多选题
例1(2021年高考数学新高考Ⅰ卷第9题)(多选题)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c为非零常数,则( ).
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样本数据的样本极差相同
分析利用统计知识中的基本知识、基本公式等,将统计中的概念、公式等基本知识交汇与融合在一起,通过平均数、中位数、标准差、极差的定义直接判断即可.
解析对于选项A,两组数据的平均数的差为c,故选项A错误;对于选项B,两组样本数据的样本中位数的差是c,故选项B错误;对于选项C,由于标准差D(yi)=D(xi+c)=D(xi),则知两组样本数据的样本标准差相同,故选项C正确;对于选项D,由于yi=xi+c(i=1,2,…,n),c为非零常数,x的极差为xmax-xmin,y的极差为(xmax+c)-(xmin+c)=xmax-xmin,所以两组样本数据的样本极差相同,故选项D正确.故选CD.
2.运算、推理类多选题
例2(2021年高考数学新高考Ⅰ卷第11题)(多选题)已知点P在圆(x-5)2+(y-5)2=16上,点A(4,0),B(0,2),则( ).
A.点P到直线AB的距离小于10
B.点P到直线AB的距离大于2
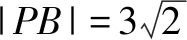
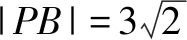
分析求出过AB的直线方程,再求出圆心到直线AB的距离,得到圆上的点P到直线AB的距离范围,判断选项A与B;画出图形,由图可知,当过点B的直线与圆相切时,满足∠PBA最小或最大,求出圆心与点B间的距离,再由勾股定理求得|PB|判断选项C与D.
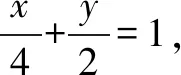
3.位置确定类多选题
例3(2021年高考数学新高考Ⅱ卷第10题)(多选题)如图1,在正方体中,O为底面的中点,P为所在棱的中点,M,N为正方体的顶点,则满足MN⊥OP的是( ).

图1
分析对于选项A,设正方体棱长为2,设MN与OP所成角为θ,求出tanθ的值,从而不满足MN⊥OP;对于选项B,C,D,作出平面直角坐标系,设正方体棱长为2,利用向量法进行判断.


图2
4.信息创新类多选题
例4(2021年高考数学新高考Ⅱ卷第12题)设正整数n=a0·20+a1·21+…+ak-1·2k-1+ak·2k,其中ai∈{0,1},记ω(n)=a0+a1+…+ak,则( ).
A.ω(2n)=ω(n) B.ω(2n+3)=ω(n)+1
C.ω(8n+5)=ω(4n+3) D.ω(2n-1)=n
分析根据创新定义,2n=a0·21+a1·22+…+ak-1·2k+ak·2k+1可判断选项A;取n=2可判断选项B;把8n+5和4n+3都化成n=a0·20+a1·21+…+ak-1·2k-1+ak·2k,可判断选项C;2n-1=1·20+1·21+…+1·2n-1可判断选项D.
解析由于2n=a0·21+a1·22+…+ak-1·2k+ak·2k+1,则有ω(2n)=ω(n)=a0+a1+…+k,故选项A正确;当n=2时,2n+3=7=1·20+1·21+1·22,可得ω(7)=3,又ω(2)=0+1=1,所以ω(7)≠ω(2)+1,故选项B错误;w(8n+5)=w(8n+4+1)=w(8n+4)=1,w(4n+3)=w(4n+2+1)=w(4n+2)+1,由A选项知,w(2n)=w(n),所以w(8n+4)=w(4n+2),即w(8n+5)=w(4n+3),故选项C正确;由于2n-1=1·20+1·21+…+1·2n-1,可得ω(2n-1)=n,故选项D正确.故选ACD.
新高考中数学多项选择题的创新引入与设置,给数学知识的设置与考查提供更多的场所,给不同层次的学生增加了得分机会,也更精准地测试和区分了不同层次学生的数学基础和数学能力水平.同样,数学多项选择题不同基本类型与相应的破解策略不断涌现,特别是基本类型与破解策略之间经常也是交叉与融合的,没有太过明显的类别,实际破解时要合理综合,巧妙应用.

