优化新概念教学提升大学生探究能力——以“数学期望”教学实践为例

罗 原

(西南科技大学理学院，四川绵阳 621000)

0 引言

数学概念(mathematical concepts)是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式，即一种数学的思维形式.在数学中，作为一般的思维形式的判断与推理，以定理、法则、公式的方式表现出来，而数学概念则是构成它们的基础[1].

大学数学中很多基本数学概念高度概括且非常抽象,数学概念是数学技能和思维培养的基础,所以应该高度重视概念教学,让学生真正理解数学概念的本质,并且在理解概念的过程中体会到其中蕴含的数学思想，达到举一反三之目的.

1 循序渐进，由浅入深，引入概念

以“概率论与数理统计”课程中数学期望教学内容为例：

同时，这个概念也是历年研考的热点之一.所以，在随机变量的数字特征的教学实践中，要牢牢地抓住数学期望这个“牛鼻子”，这个矛盾的“主要方面”，进而达到让学生全面、系统、深刻地理解、掌握和运用数字特征来解决问题的教学初衷.

以“掷骰子”的游戏为引子.假设掷骰子10次，得到如下记录：

考虑出现点数的平均值？

随即引导学生思考随机试验的次数为“无穷”的时候，随机变量的“平均值”还存在吗？该如何计算？又有什么应用？

1.1 提出概念

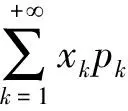
由上述定义可以看出，随机变量的数学期望本质上是一“加权平均值”，是概率意义下的平均值，而概率就是这里的“权重”.同时由于概率是频率的“极限”，所以，这个平均值含有对“未来”进行“展望”的意味.但对初学者而言，准确理解这个概念的内涵并且熟练运用并不是很容易的.同时还要注意，由于数学期望的定义要求“绝对”收敛，所以一个随机变量可以有平均值或中位数，但其期望值却是不一定存在的.

1.2 凸显概念“平均值”之属性，引导学生探究新概念内涵

据笔者追踪观察，多数学生初次接触到数学期望这个概念时，普遍有“抓不住”概念本质的感觉.那么，在教学中，首要任务就是破解其“神秘感”，凸显概念的“平均值”属性.

例1[3]设有某国家盛行“重男轻女”，家庭若第一胎为女孩，则必生第二胎；若第二胎仍为女孩，则必生第三胎；……直到生男孩为止.那么，这个国家人口男女比例如何？

这个结果让不少同学感到意外，也品尝到探究新事物的妙趣.此时，老师可抓住时机，对怎样理解数学期望即是“加权平均值”以及概率即是“权重”这个“内涵”做及时阐述和引导，以期尽快掌握这个新概念的根本特质.

1.3 提升学生课堂主体地位，引导探究问题之良好习惯，提高解决问题能力

美国著名教育家、哲学家、心理学家约翰·杜威说过：“科学教育不仅仅是要让学生学习大量的知识，更重要的是要学习科学研究的过程或方法”.而教育家施瓦布所倡导的探究教学中，他认为学习“不在于占有的信息，而在于拥有的探究能力”[1].

学习新概念的最终目的，在于运用好概念，解决实际问题.在教学实践中，应积极发挥学生的课堂主体地位作用，调动其探究兴趣.

在数学期望的概念里，概率扮着“平均值”的“权重”这个重要角色，同时由于概率又是频率的“极限”，所以，这个平均值含有对“未来”进行“展望”的意义，这是在“平均值”基础上的又一个值得探究的“爆发点”，与“平均值”一起，构成了“数学期望”的“双核”，应着重加以引导[3].

例2[4]设有甲、乙二人各出70元设立奖金，竟猜马路上驶过汽车牌号尾数的“单”与“双”(假设每轮都有胜负).规定先猜中5次者获得全部奖金140元.现游戏因为意外原因临时终止.此时甲已猜中4次，乙已猜中3次.请问应该如何分配该笔奖金？

引导分析：平均分配显然对甲不公平.或者把奖金分成7份，甲4乙3，即甲得80元，乙得60元.这是个貌似“公平”的方案，但这样分配是不是“合理”的？甲、乙应该按什么比例瓜分奖金才算“合理”呢？

可以这样设想，在现有情况下游戏继续进行下去会是什么结果？

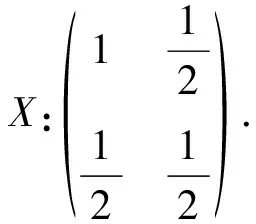
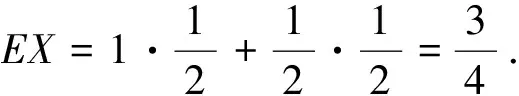
这个分配方案是否“合理”呢？

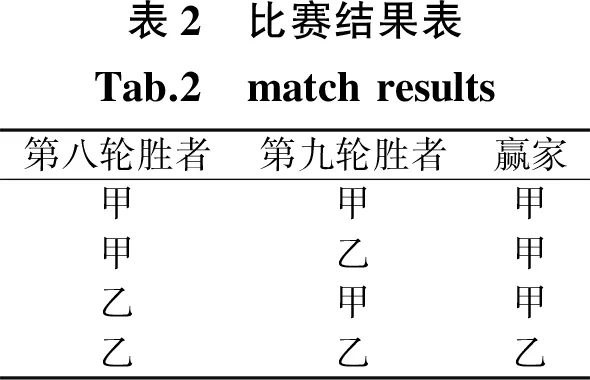
方案二、假设游戏全部完成(即将全部(至多)九次比赛进行完毕)，结果如表2，

例3[5](考研复习)笔者曾在班上引导学生做过的实验:随机地抽取5位同学，请他们报出自己的学号：5,13,30,64,69.由此推算该班学生人数？

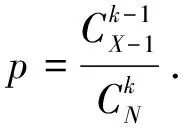
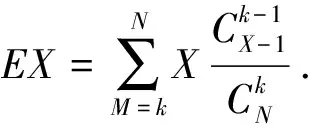
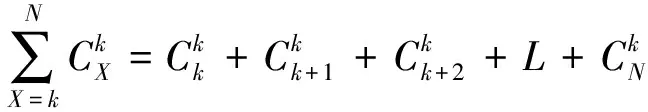
例3同样利用了数学期望“双核”“内涵”，来对随机现象的某种“统计规律性”进行“推断”，在实践中具有一定的应用价值.

教学实践中还可以组织同学举一反三，自我设计一些有趣的实验，比如对聚会人数，马路上汽车流量，电话公司客户数等等做出某种“推断”，进一步达到强化理解和熟练运用的目的.

2 总结

新概念教学是数学教学过程中极其重要的环节，而讲好新概念的关键在于发挥学生课堂主体地位作用，以问题为导向，让其全过程置身其中，充分调动其探究积极性.从课堂效果观察，成效是明显的.当然，实践往往是极其丰富多彩的，并不存在一种适合所有概念教学的“万能模式”.但只要抓住概念本质，凸显概念“内涵”，以生为本，问题导向，那么，实现教学目的是有保证的.此外，要实现这个目标，很大程度上还取决于在实际问题中的观察与思考.这样在客观上就要求老师要时刻关注生活中的“司空见惯”现象及其背后蕴含的科学道理和逻辑关系，并将之予以提炼，让“呆板”的数学概念在丰富的实践中变得栩栩如生，趣味盎然.