两相环境下EPDM绝热层多因素耦合烧蚀预估①
王 乐,冯喜平,陈嘉辉,卢景旭,梁 群,侯 晓
(西北工业大学 航天学院 燃烧、热结构与内流场重点实验室,西安 710072)
符号表
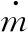

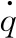
j组分扩散率dc燃烧室直径
ρ密度D组分扩散系数
u、v流速A指前因子
h对流换热系数E活化能
hD传质系数R气体常数
cp燃气定压比容f总气化分数
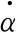
p压强y绝热层厚度
M分子量n质量通量
Mgw燃气平均分子量α颗粒冲刷角度

T温度ε孔隙率
Ck当量热容
hs、hw、hr烧蚀壁焓值、气动壁焓值、恢复焓值
下标
c 碳化层 d 扩散控制机制
vir 基体层 e 附面层外缘
pyr 热解层 g 气体
ch 动力学控制机制 w 壁面
i组分 p 颗粒
0 引言
固体火箭发动机工作过程中,为确保燃烧室结构的完整性,常采用EPDM或改性EPDM绝热层来保护燃烧室[1-3]。而在燃烧室的高温、高压、两相流动燃气环境中,绝热层的设计与其烧蚀预估密切相关。固体发动机燃烧室内的流动多为两相流动,在此环境下绝热层的烧蚀由热化学反应造成的热化学烧蚀、燃气流动造成的气流剥蚀和离散相颗粒撞击造成的颗粒侵蚀共同组成。
目前,国内外针对EPDM绝热层不同因素耦合情况下的烧蚀性能进行了一些理论与实验研究。KOO等[4]研究了有无颗粒侵蚀情况下的烧蚀性能,实验结果表明,颗粒侵蚀条件下的绝热层烧蚀率是无颗粒侵蚀情况下的2~12倍,说明烧蚀研究中不能忽略颗粒侵蚀;YANG等[5]数值模拟了酚醛树脂等炭化类绝热材料在热化学烧蚀及颗粒侵蚀耦合作用下的烧蚀性能,并与实验值进行了比较。研究表明,热化学烧蚀会加剧颗粒侵蚀,反过来颗粒的作用也加剧了热化学烧蚀;DIMITRIENKO[6]将烧蚀分为体积烧蚀和表面烧蚀,其中体烧蚀主要指热解,将会使材料密度下降;面烧蚀指烧蚀表面的质量损失,将会使结构厚度变化。CURRY等[7]建立了更为复杂的双区体烧蚀模型,分为多孔介质区和固体区,在多孔介质区发生了复杂的物理化学过程,其中包含沉积反应。CAUTY等[8]将超声技术应用于绝热材料的数据收集和估计火箭发动机表面的热载荷,并证明了该方法对于热流估计的准确性。
国内对EPDM绝热层的烧蚀问题同样也进行了深入研究。何洪庆等[9]对炭化型热防护材料EPDM进行了研究,采用气动热化学烧蚀机理,扩散和化学动力学双控制机制,其中化学表面反应加入了SiO2的反应模型,并计入气流与粒子的侵蚀,其中粒子侵蚀公式采用经验公式,建立EPDM的烧蚀模型。李江等[10]研究了颗粒浓度和冲刷速率对绝热材料烧蚀的影响。在实验的基础上,建立了冲刷状态与炭层厚度的关系,并采用传统的炭化烧蚀模型进行烧蚀计算。王娟等[11]在颗粒冲刷条件下进行了EPDM烧蚀实验,分析结果表明,认为某一种颗粒速度为临界速度,当临界速度高于冲刷速度时,炭化烧蚀率受粒子浓度、速度和角度影响较小,当临界速度低于冲刷速度时,炭化烧蚀率随速度、角度的增加而急剧增大。王书贤等[12]分析了气相环境下不同燃气速度对EPDM绝热层炭化烧蚀率、炭化层结构特征以及成分分布等的影响。研究发现,燃气速度较低时,烧蚀以热解炭化为主;燃气速度较高时,炭化层的机械破坏显著。对于EPDM绝热层烧蚀预估,综合考虑三因素的研究相对较少,李强等[13]耦合前述三种因素,采用热化学反应在碳化层内部进行的假设,以碳化层的孔隙率为纽带,建立了热化学烧蚀、颗粒侵蚀和气流剥蚀的耦合烧蚀模型,初步确定热解气体沉积是炭化层中致密结构的形成的主要原因,并根据实验结果及沉积理论拟合致密层数值算法。研究表明,建立的模型在烧蚀率预估方面具有较好的精度。刘洋等[4]研究了热解气和燃气在碳化层多孔结构中的化学气相沉积和热化学烧蚀过程。以及气体和颗粒在碳化层上的侵蚀过程,数值计算结果表明,实验结果与数值计算结果的最大误差小于12%,数值结果与实验结果偏差还有待降低。
本文就EPDM在固体发动机工作环境下的流固耦合烧蚀工程预估展开研究。基于绝热层的消耗反应,即炭化层与推进剂燃气之间的反应仅发生在炭化层表面的假设,通过炭化层表面孔隙率实现热化学烧蚀、颗粒侵蚀和气流剥蚀等的烧蚀耦合,采用动边界热传导差分法进行数学模型的求解,实现了固体火箭发动机两相环境下EPDM绝热层炭化烧蚀率的工程预估。
1 物理模型
图1为烧蚀后绝热层材料内部的组成和两相环境下绝热层表面外和绝热层内部发生的物理现象。
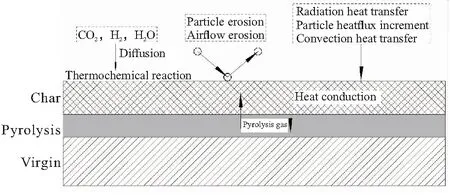
图1 EPDM绝热层多因素烧蚀示意图
发动机工作过程为:发动机工作后(点火并燃烧后),首先,推进剂燃烧产生两相高温高压燃气;然后,高温高压燃气在贴附有绝热层的燃烧室内流动;最后,燃气由喷管喷出产生推力。在这一流动过程中,由于高温高压燃气沿贴附于燃烧内表面的绝热层外表面流动,两相燃气与绝热层外表面之间发生对流和辐射换热,这样使绝热层表面温度升高。同时,由于绝热层内部温度梯度的存在,绝热层内部发生热传导,将表面导入的热量向绝热层内部传递,使得绝热层内部温度升高。由于绝热层为高分子复合材料,当温度升高时,其内部发生化学变化,材料物理性能也会发生变化。
在这一过程中,对流换热和热传导使得绝热层表面温度升高,当绝热层表面温度达到绝热层材料的热解温度时,表面材料发生热解,随着时间的进行热界面加厚形成热解层;随着热交换过程的进一步进行,材料表面温度达到炭化温度时,材料表面发生炭化,这一过程中伴随材料中极大部分高聚物分解成低分子气体溢出表面,留下多孔焦炭残渣,并和原先加入基体的无机添加剂一起形成炭化层。
发动机工作过程中,由于炭化层的多孔性质和气体扩散性,来流燃气中氧化性组分和热解气体中最终裂解产生的氧化性气体同炭化层中的碳发生化学反应,吸收热量的同时使得炭化层表面不断退移。此外,高速燃气对绝热层表面产生冲刷以及燃气中Al2O3颗粒会撞击绝热层表面,引起绝热层表面附近的炭化层表面的进一步退移。
为进行烧蚀机理研究,设计了EPDM绝热层三因素耦合烧蚀的实验器,实验原理如图2所示。
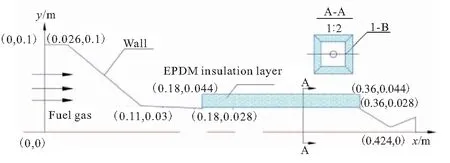
图2 EPDM绝热层实验原理图
由图2可见,4片EPDM绝热层烧蚀试件分别安装于烧蚀实验发动机方形试验段的4个侧面,每片绝热层试件的y方向厚度为0.016 m,x方向长度为0.18 m。燃烧室高温两相燃气通过收敛段加速进入实验段,并流过EPDM绝热层试件表面对试件进行烧蚀的同时,燃气经过试验段后继续加速,最后通过喷管流出。针对该耦合烧蚀模型,粒子撞击角度为0,因此该模型主要受到气流剥蚀影响。
根据设计实验工况,确定计算工况:发动机工作压强7 MPa,工作时间7 s,喷管喉径10.8 mm,EPDM绝热层厚度0.016 m,长度0.18 m。实验采用的推进剂为高能复合推进剂,燃温3536 K,其中铝粉含量16%。实验可得绝热材料烧蚀后平均体孔隙率为0.562。
2 数学模型
2.1 绝热层表面热化学烧蚀模型
基本假设:
(1)绝热层表面燃气流动为二维冻结流;
(2)化学反应仅发生于绝热层表面;
(3)气体流动符合理想状态方程;
(4)绝热材料不发生膨胀或收缩;
(5)表面遵循质量、动量和能量守恒定律。
绝热层表面的质量、动量和能量传递关系如图3所示,根据该传递关系建立守恒方程。
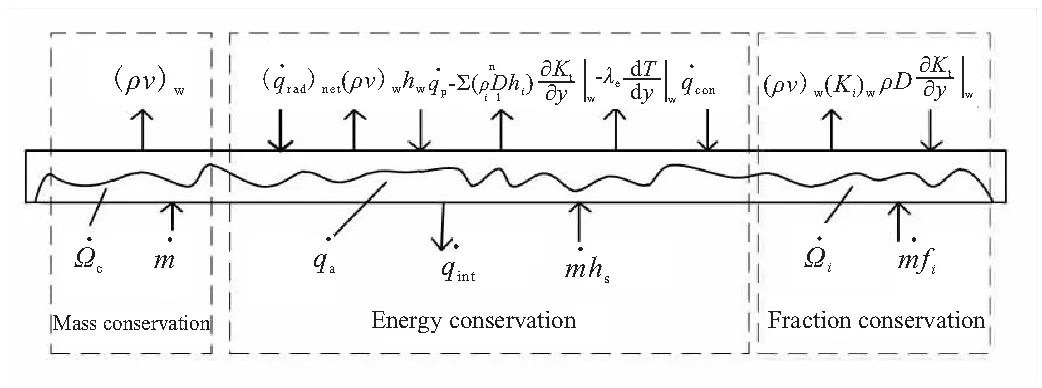
图3 绝热层表面质量、动量和能量守恒关系
(1)质量守恒方程
热解气体流入控制体的质量流率+化学反应产生气体质量流率=绝热层表面流出气体的质量流率,即:
(1)
(2)能量守恒方程
热解气体流入热流+热化学反应热效应+净热辐射热流+颗粒带来的热流+对流换热流入热流=导入绝热层内部热流+流出气体带走的焓+分子运动扩散带走热流+燃气与绝热层热传导热流,即
(2)
(3)组分守恒方程
绝热层表面流出第i种气体的组分质量率=浓度梯度扩散的第i种组分质量率+化学反应产生的第i种组分质量率+热解气体产生的第i种组分质量率,即:
(3)
绝热层表面的三个化学反应为
C(s)+CO2=2CO
C(s)+H2O=CO+H2
2C(s)+H2=C2H2
将不参加壁面化学反应的组分都折合归纳入N2,将组分按次序排列为H2O、CO2、H2、CO、C2H2和N2,并依次对应表示为i=1,2,…,6。化学表面反应方程组缺少热解气体组分数据,取热解气体组分质量分数f1=0.35,f2=0.32,f3=0.18。
绝热层的热化学烧蚀,一方面受化学反应动力学控制;另一方面受燃气组分通过附面层向壁面的扩散速率控制,即上述三个反应为双控制机制[15]。双控制下氧化性组分的质量消耗率为
(i=1,2,3)
(4)
式中Ai为指前因子,A1和A2均取0.011 357 kg/(m2·s·Pa),A3=0.000 711 22 kg/(m2·s·Pa);Ei为反应活化能,E1和E2均取236 500 J/mol,E3=284 600 J/mol;pw,i为i组元在壁面处的分压;R为通用气体常数;Tw为气动壁温度;pw,i为气动壁面不同组分分压;ρe为燃气密度;ue为燃气速度;CH为传热传质系数;Kie为燃气中不同组分浓度[16]。
表面化学反应中组分的质量生成率为
(5)
其中,M为相对分子质量。将式(5)代入到绝热层表面控制方程式(1)和式(3),得绝热层表面单位面积的碳消耗率为
(6)
则绝热层线烧蚀率为
(7)
因为实验后绝热层烧蚀试件的炭化层与基体层之间存在明显间隙,同时炭化层会出现膨胀等现象,如采用线烧蚀率来表征绝热层的烧蚀性能将存在较大误差。因此,本文采用炭化烧蚀率rc表征绝热层的烧蚀性能,其定义为:炭化烧蚀率=(试件初始厚度-实验后试件基体层厚度)/实验发动机工作时间。
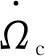
(8)
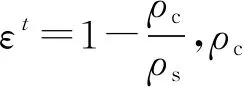
根据热化学烧蚀实验结果[18],炭化层内部孔隙率逐渐增大,与炭化层厚度δ成线性关系,t+Δt时刻炭化层内部各点孔隙率采用经验关系式:
(9)
2.2 颗粒侵蚀计算模型
根据多孔材料强度的概念,孔隙率大小与炭化层强度存在一一对应的关系。由于颗粒侵蚀强度与燃气流速、颗粒撞击角度、炭化层强度等均有关系,作用机制复杂。因此,颗粒侵蚀计算模型也常采用基于实验的经验关系式。
根据现有实验结果,颗粒侵蚀炭化层烧蚀表面的临界孔隙率εc1可表示为[19]
(1)临界速度以下(v<32 m/s)
(10)
(2)临界速度以上(v≥32 m/s)
(11)
式中np为颗粒冲刷质量通量;vp为颗粒撞击速度;α为颗粒撞击角度。
2.3 气流剥蚀模型
影响绝热层气流剥蚀的主要因素有气流速度、环境压强、炭化层高温结构强度、热解气体逸出产生的粘性力和内压等,这些影响气流剥蚀因素的详细作用机制目前还不清楚。因此,气流剥蚀计算模型只能采用经验关系式,即以实验测得的表面孔隙率为气流剥蚀后炭化层表面的临界孔隙率。
在认为气流主要通过剪切力实现剥蚀的前提下,根据实验结果拟合得到炭化层临界孔隙率和炭化层表面剪切力的关系式为[10]
εc2=0.2+0.07×0.896τ
(12)
其中,εc2为气流剥蚀对炭化层表面的临界孔隙率。且剪切力与燃气参数的实验关系式如下:
(13)
2.4 绝热材料传热分析数学模型
由物理模型可知,EPDM绝热材料烧蚀后可分为三层,针对不同层区有不同热传导方程:
(1)炭化层
(14)
(2)热解层
(15)
式中 ΔHp为材料的热解吸热率。
热解层的密度、热导率和比热可近似认为是随温度线性变化的[20]。即:
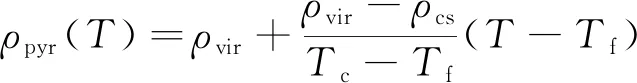
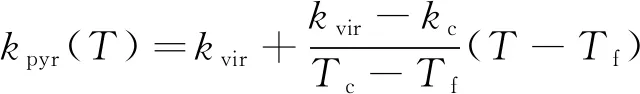
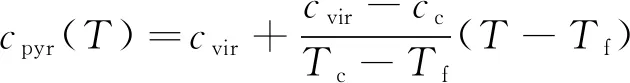
(3)基体层:
(16)
绝热层表面温度不同时,传入内部热流量不同,定义绝热材料开始热解温度为Tf=600 K,绝热材料开始炭化温度为Tc=1200 K。
(4)初始条件
t=0时,T0=Ts。
(5)边界条件
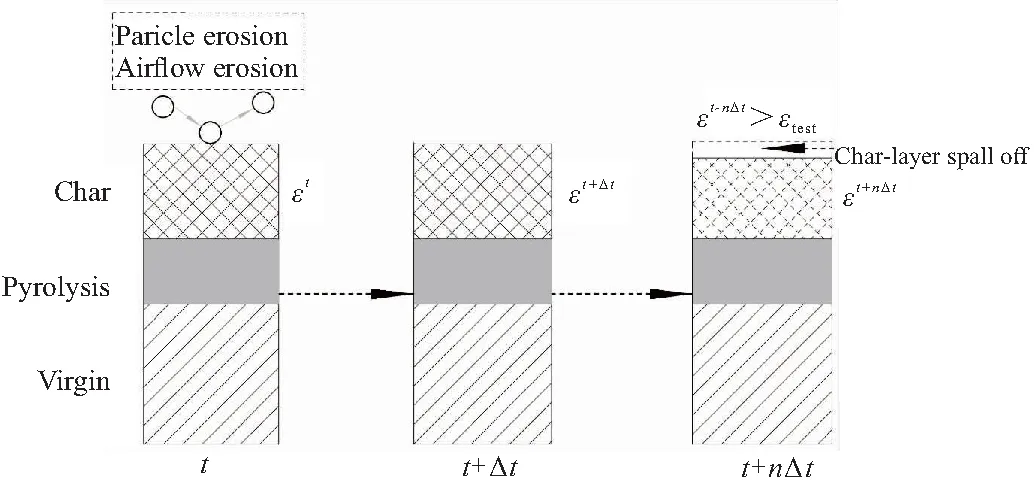
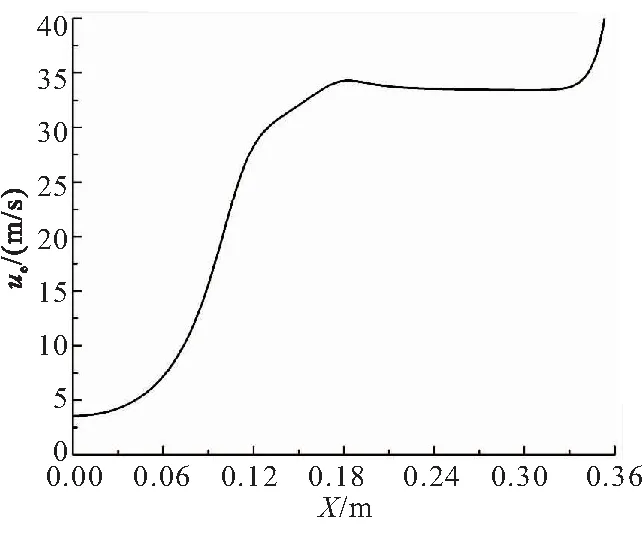
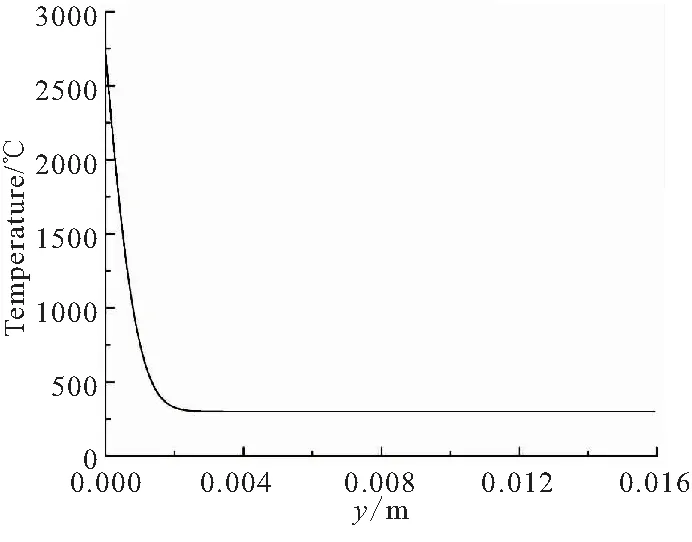
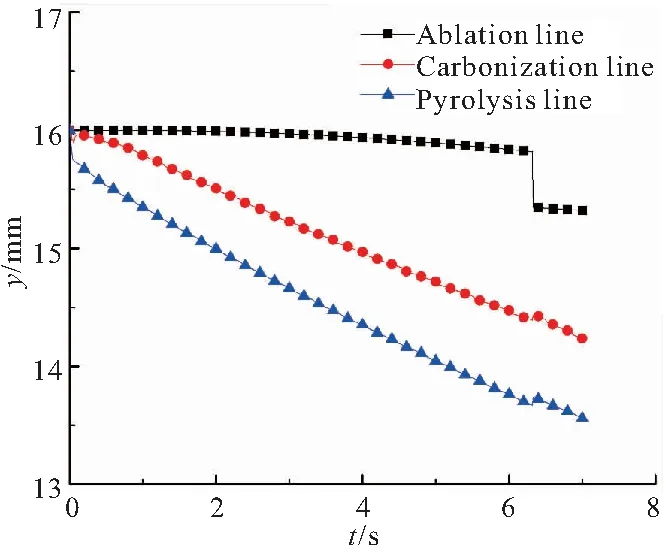
1)T (17) 2)Tf (18) 3)T>Tc时,绝热材料表面开始炭化,绝热材料开始形成三层结构,此时: (19) 在绝热材料背面假设为绝热,则: (20) 2.4.1 壁面温度求解 壁面温度分为气动壁温度和烧蚀壁温度,这是由于化学反应不是在面内进行而是在控制体内进行,控制体上下表面温度不一致。可用气膜分析法找到气动壁温度、烧蚀壁温度和气相附面层外燃气温度的关系如下: (21) 式中a为气膜厚度,实验结束后通过电镜扫描测量获得。 实际上,当表面没有炭化时,气动壁温度等于烧蚀壁温度,但燃烧室温度逐渐升高,开始烧蚀时环境温度没有达到推进剂绝热燃烧温度,若仍采取绝热燃烧温度计算会造成辐射热流量和对流换热量异常大,不符合实际过程。因此,采取上述方法对壁面温度进行初始计算,以符合实际过程。 2.4.2 辐射热流计算 可用黑体辐射定律计算辐射热流量,即 (22) 2.4.3 附面层热传导求解 燃气在绝热层表面流动可为层流流动,也可为湍流流动。认为是层流流动时可用非定温绕流平壁的温度型方程来求解燃气与绝热层之间的热传导热流。 本次计算中采用简化算法,使用对流换热关系式进行求解,表达式如下: (23) 2.4.4 焓值计算 焓值计算包括气动壁处焓值、烧蚀壁处焓值和恢复焓值的计算。 气动壁处焓值: Hw=ceTw (24) 烧蚀壁处焓值: Hs=ceTs (25) 恢复焓值: (26) 式中k为燃气比热比;Me为燃气马赫数。 2.4.5 化学反应热效应计算 化学反应热效应的计算思路:反应热×每种反应碳的消耗量。则计算式为 (27) 该反应下,C与H2O、CO2、H2的化学发应热分别为-4.688、-7.621、-7.428 kJ/mol。 2.4.6 颗粒冲刷热增量模型 颗粒冲刷壁面的热增量计算关系式为 (28) 式中Np为颗粒浓度。 多因素耦合计算模型是以炭化层烧蚀表面的表面孔隙率为耦合参数,对热化学烧蚀、颗粒侵蚀和气流剥蚀等各烧蚀模型进行耦合,建立了多因素耦合计算模型。绝热层多因素耦合计算模型如图4所示。 图4 绝热层多因素耦合计算模型示意图 绝热层非稳态多因素耦合烧蚀性能计算步骤: (3)如此循环计算,即可得到烧蚀表面各点的炭化线位置和炭化烧蚀率。 为了便于将计算结果与实验结果进行比较,以烧蚀实验装置的实验段为物理模型,采用二维可压缩流动假设,设置流动入口边界条件为压力入口,出口边界条件为压力出口,实验器壳体为绝热壁面,两相流采用DPM模型,粒子含量取燃气流量的15%。计算得到烧蚀实验发动机烧蚀气流内流场结果如图5所示。 (a)Distribution of velocity 由图5可知,烧蚀过程中试验段(参见图2,X=0.18~0.36 m)燃气速度为32 m/s,燃气压力为7 MPa,燃气温度为3536 K,且气流的速度、压力、温度沿X方向无明显变化,粒子冲刷质量通量为87 kg/(m2·s),颗粒撞击绝热层表面速度为24 m/s。多因素耦合烧蚀性能计算时,选取绝热层平均炭化烧蚀率作为性能表征,并将其与1-B处的炭化烧蚀率理论计算值rc进行比较,以验证多因素耦合烧蚀模型。 在前一节中给出的两相烧蚀气流作用下,绝热层温度分布如图6所示。绝热试件1的1-B处(图2)典型的烧蚀性能计算结果如图7~图10所示。 图6 EPDM绝热层温度分布 图7 烧蚀线、炭化线和热解线位置随烧蚀时间的变化图 图8 烧蚀表面温度随烧蚀时间的变化 图9 烧蚀两相流各热流率随烧蚀时间的变化 图10 炭化烧蚀率随时间的变化 由图7和图8可知,随着烧蚀时间的增加,绝热层表面温度不断升高、炭化层与热解层厚度逐渐增加、炭化层内部孔隙率不断增大,材料烧蚀6.4 s后,炭化层内部各点孔隙率的平均值≥EPDM绝热层烧蚀实验测得的炭化层平均孔隙率时而发生剥离,导致绝热层表面发生烧蚀剥离,从而使炭化层厚度骤然减小,烧蚀表面温度骤然降低,并随着烧蚀的进行,温度重新升高。热解层和原始层厚度所受影响较小。烧蚀继续进行到7 s时,烧蚀表面退移了0.69 mm。 由图9可知,绝热层表面处不同热流率随时间的变化,其中辐射换热率的量级是106W/m2,对流换热率与颗粒带来的热流率是105W/m2,其余热流率较小,同时由计算结果可见,当烧蚀进行到6.4 s时,绝热层剥离会导致表面温度降低,进而会造成辐射换热率以及对流换热率的增加。 图10为炭化烧蚀率随时间的变化曲线,随着烧蚀的进行,炭化烧蚀率逐渐达到稳态为0.21 mm/s;当烧蚀进行到6.68 s时,绝热层表面发生剥离,由于气流剥蚀、颗粒侵蚀带来的热流率较辐射换热率小一个量级,因此其对炭化烧蚀率影响较小,炭化烧蚀率保持稳定。烧蚀继续进行到7 s时,炭化烧蚀率为0.213 mm/s。 绝热层烧蚀实验的试件表面测点位置如图11所示。 图11 绝热层表面测点位置图(单位:m) 实验后,测得绝热层表面不同位置所对应的烧蚀厚度。之后,对相同X位置的值取平均烧蚀厚度,可得沿X轴不同位置的平均炭化烧蚀率,见图12。 图12 实验后测得炭化烧蚀率 由图12可得绝热层平均炭化烧蚀率0.203 mm/s。与理论计算炭化烧蚀率0.22 mm/s比较,理论计算误差小于10%,误差主要来源于炭化层比热容以及热导率在高温下变化的影响。由此验证了本模型在热化学、气流剥蚀以及颗粒侵蚀下的烧蚀率预测能力。 本文所提的方法可用于不同发动机或同一发动机不同部位的两相环境下EPDM绝热层的烧蚀预估。 根据上述内容,对不同燃气温度、燃气压强、颗粒含量下的耦合烧蚀模型进行了分析计算,计算结果如表1所示。可见,燃气温度对绝热层炭化烧蚀率的影响较大,因为绝热层表面化学反应速率主要受燃气温度影响,燃温越高,化学反应速率越快,加速烧蚀线、炭化线、热解线退移,导致炭化烧蚀率变化幅度较大;燃气压强以及颗粒含量对炭化烧蚀率的影响相对较小,炭化烧蚀率随压强的升高以及颗粒含量的增大呈上升趋势。 表1 不同烧蚀影响因素下的炭化烧蚀率 (1)随着烧蚀的进行,绝热层表面温度不断升高、炭化层与热解层厚度逐渐增加、炭化层内部孔隙率不断增大;当炭化层内部各点孔隙率的平均值 EPDM绝热层烧蚀实验测得的炭化层平均孔隙率时发生剥离,导致绝热层表面发生烧蚀剥离,从而使炭化层厚度骤然减小,烧蚀表面温度骤然降低并随着烧蚀的进行,温度重新升高。热解层和原始层厚度所受影响较小。 (2)绝热层理论计算的炭化烧蚀率为0.22 mm/s,与实验平均炭化烧蚀率0.203 mm/s的误差为8.37%,且误差主要来源于炭化层比热容及热导率在高温下变化的影响。由此验证了本模型在热化学、气流剥蚀及颗粒侵蚀下的烧蚀率预测能力。 (3)燃气温度相对于燃气压强以及颗粒含量对绝热层炭化烧蚀率的影响较大。燃温越高,化学反应速率越快,加速烧蚀线、炭化线、热解线退移,炭化烧蚀率增大;炭化烧蚀率随压强的升高以及颗粒含量的增大呈上升趋势。

2.5 多因素耦合计算模型
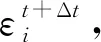

3 结果分析与讨论
3.1 两相烧蚀气流内流场计算结果与分析
3.2 绝热层烧蚀性能计算结果与分析

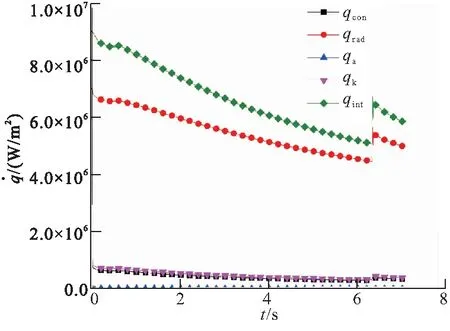
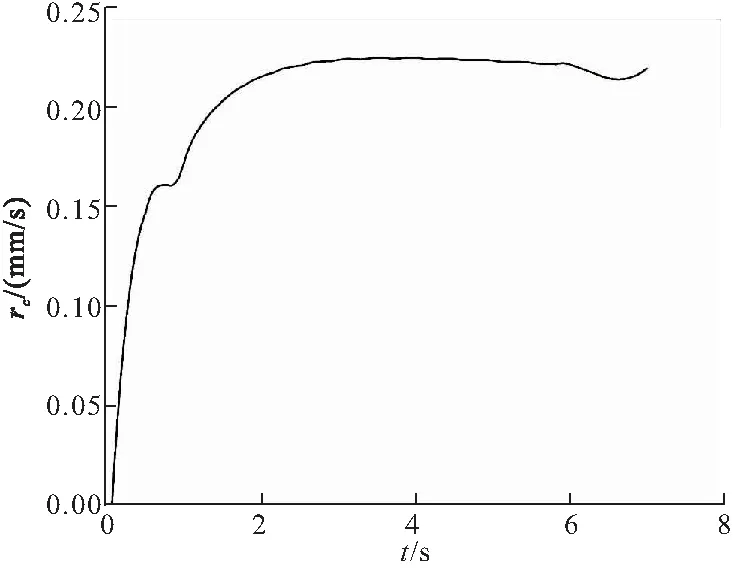
3.3 烧蚀性能数值解与实验值对比分析

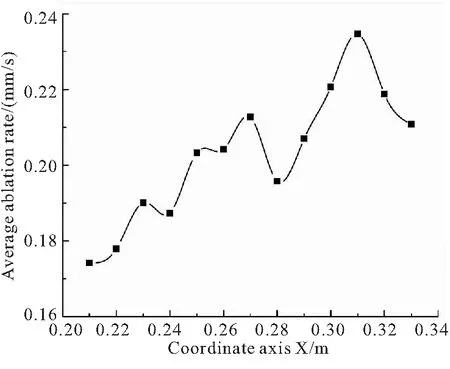
3.4 不同烧蚀影响因素下炭化烧蚀率分析
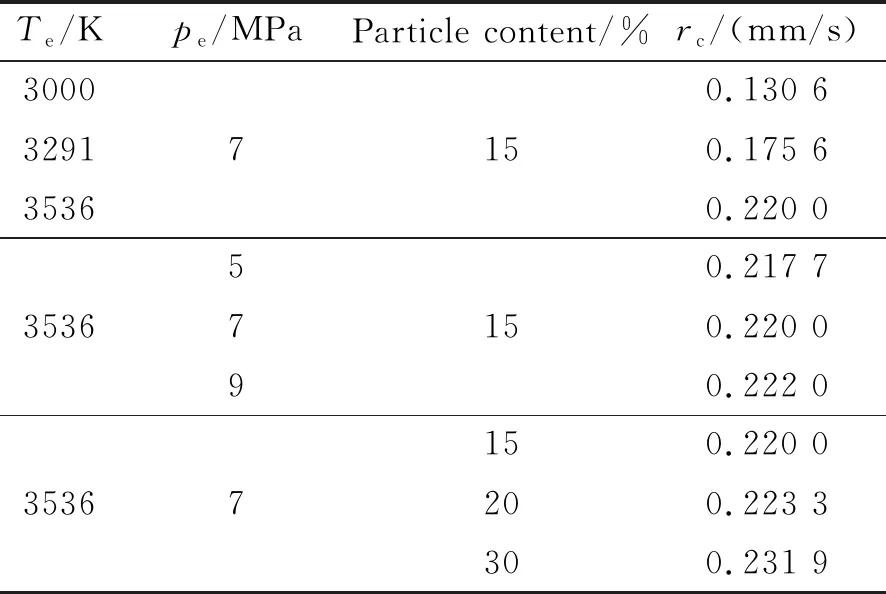
4 结论

