动能定理是否有单方向的“分解式”
孙永茂
(赣州市第三中学 江西 赣州 341000)
1 问题引出
中学阶段有三大观点可以解决力与运动的相关问题,分别是力的观点、动量观点和能量观点,对于牛顿运动定律、动量定理和动量守恒定律,都可以分方向进行运用.对于动能定理,表述的是功与能的关系,功和能都是标量,可以分方向运用动能定理吗?也就是说,动能定理是否有单方向的“分解式”?我们从一道力学题入手进行分析.
【例1】如图1所示,一质量为m,电荷量为q的正电粒子在匀强电场中运动,A和B为其运动轨迹上的两点.已知该粒子在A点的速度大小为v0,方向与电场方向的夹角为60°,它运动到B点时速度方向与电场方向的夹角为30°.不计重力,求A,B两点间的电势差.

图1 例1题图
在教学过程中,发现学生有以下两种解法.
解法1:带电粒子只受电场力,粒子沿电场方向做匀加速直线运动,垂直电场方向做匀速直线运动,有
vBsin 30°=v0sin 60°
(1)
粒子从A到B点,由动能定理
(2)
联立式(1)、(2)得
解法2:带电粒子只受电场力,所以粒子速度的改变是由电场力决定的,电场力仅改变粒子沿电场方向的速度大小,在沿电场方向使用动能定理
(3)
物体在垂直电场方向做匀速直线运动,有
vBsin 30°=v0sin 60°
(4)
联立式(3)、(4)得
【分析】对比两种解法,计算结果相同,对于解法1,教师和学生都非常认同.但对于解法2,咨询多位教学经验丰富的物理老师,发现此解法存在非常大的争议,教师之间存在两种不同的观点:
观点1:解法2错误,因为动能定理是标量式,不能进行矢量分解,故不可以单方向运用动能定理,解法2的计算结果与解法1相同只是计算的巧合,不能当做规律进行推广.
观点2:解法2正确,动能定理是标量式是毋庸置疑的,但标量也可以分解,如总功就可以分解为各个力做功之代数和.同理,对于动能的总变化量可以为各方向的动能变化量的代数和[1,2].本题中,在沿电场方向和垂直电场方向建立直角坐标系,再分别求解各方向的动能的变化量,则有
F合s=ΔEkx+ΔEky
又因物体仅受水平方向的电场力,则ΔEky=0,所以有F合s=ΔEkx,即解法2是正确的.
以上两种观点哪个是正确的?此带电粒子的合力为水平方向,即解法2在水平方向使用了动能定理,而持观点1 的教师不认同此解法.两种观点的争论点围绕于是否存在单方向的动能定理“分解式”.接下来进行理论分析,论证是否存在动能定理的单方向“分解式”.
2 理论分析
动能的大小和速度有关,而速度是矢量,故建立三维直角坐标系O-xyz,如图2所示,各方向的单位分矢量为i,j和k,合力为F,位移为s,初速度为v1,末速度为v2,由矢量的标积,可以计算以下物理量.

图2 三维直角坐标系
合力做的功为
W=F·s=
(Fxi+Fyj+Fzk)·(sxi+syj+szk)=
Fxi·sxi+Fxi·syj+Fxi·szk+Fyj·
sxi+Fyj·syj+Fyj·szk+Fzk·
sxi+Fzk·syj+Fzk·szk=
Fxsx+Fysy+Fzsz
动能的变化量
由动能定理:W=ΔEk,即
据力和运动的独立性,在x方向上
得
即ΔWx=ΔEkx
在y和z方向,同理可得
即
ΔWy=ΔEkyΔWz=ΔEkz;
将3方向关系式累加也可得
Fxsx+Fysy+Fzsz=
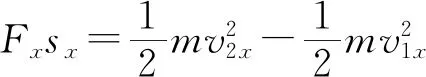
3 适用条件
通过理论分析,证明了动能定理存在类似于“分量形式”的单方向“分解式”,那此规律存在条件吗?我们以一道例题入手进行分析.
【例2】质量为m的物体静止于地面上,现有两个大小相等且互成60°的力F同时作用于物体,经时间t后,物体的速度为v,求其中一个力做的功.
常规解法:物体做初速度为零的匀加速直线运动,由动能定理

(5)
两个力大小和沿力方向上的分位移大小相同(s1=s2),如图3所示,故两力所做功相同,则每个力做的功

图3 位移分解
(6)
由式(5)和(6)得
错解:将v沿两分力方向分解为v1和v2,由图4所示,可知

图4 速度分解
由动能定理的“分解式”,一个力做的功为
分析:在错解中,似乎运用了动能定理单方向的“分解式”,但发现计算结果是错误的,说明动能定理单方向的“分解式”在运用的时候存在条件.到底是什么条件?不难发现,之前推导单方向的动能定理“分解式”是建立在直角坐标系的基础上的,如果不是直角坐标系下的分解,而是斜角坐标系下的分解,是否还有相同的结果?我们运用向量的相关知识进行分析.
情境创设:物体在合外力为恒力F的作用下以初速度v0开始做匀加速直线运动,经时间t后,位移为s,末速度为v.
分析:建立斜角坐标系xOy,如图5所示,其中x轴和y轴的夹角为θ,之后将力F和位移s和速度v0,v按平行四边形定则分解到x轴和y轴.

图5 力、位移和速度分解
对于总功,运用向量求解总功为
W=F·s=(F1+F2)·(x+y)=
F1·x+F1·y+F2·x+F2·y=
F1x+F1ycosθ+F2xcosθ+F2y
由此可见,“总功”和“分力的功”也不是简单的标量相加.
对于动能,与速度有关,速度又是矢量,先对速度进行矢量分解,再用向量求解,有

由此可见,“合动能”和类似于分解式的“分动能”并不是简单的标量相加,其运算规则更加的复杂.综上所述,功和动能的分解规则不是简单的标量合成,且两者的运算规则相同.
由动能定理

当时θ=90°时,有
此时单方向动能定理的“分解式”才能使用,即需建立直角坐标系,将力和速度分解到坐标轴上.

再回顾例题2,以其中一个力F的所在方向为x轴建立直角坐标系,如图6所示,其中F1,s1,v1分别是力F,位移s,速度v在x轴上的分量,在x轴上运用动量定理的“分解式”,有

图6 力、位移和速度分解
又
F1=Fcos 60°s1=scos 30°v1=vcos 30°
4 案例运用
利用动能定理单方向的“分解式”可以快速解决一些相对复杂的问题,接下来看到以下例题.
【例3】在水平向右的匀强电场中,如图7所示,场强为3 V/m,一电荷量为2 C的小球从A点竖直向上抛出.如图7所示,运动轨迹中的A,B两点在同一水平线上,M为轨迹的最高点.小球抛出时的动能为8 J,在M点的动能为6 J,不计空气的阻力.求:

图7 例3题图
(1)小球水平位移x1与x2的比值;
(2)小球落到B点时的动能EkB;
(3)小球从A点运动到B点的过程中最小动能Ekmin.
解:(1)沿水平和竖直方向建立直角坐标系,如图8所示.在竖直方向,小球受重力,做竖直上抛运动,又A,B两点等高,所以A→M和M→B所用时间相同.在水平方向上,小球仅受电场力,做初速度为零的匀加速直线运动,由初速度为零的匀变速直线运动规律,得x1∶x2=1∶3.

图8 运动分解
(2)小球从A→M,M点为最高点,则M点的速度水平,在水平方向上运用动能定理的“分解式”为
WAM电=EkMx-EkAx
其中
EkMx=6 JEkAx=0 J
得WAM电=6 J.
又x1∶x2=1∶3,则
A→B,WAB电=4WAM电=24 J
小球从A→B,由动能定理,得
WAB电=EkB-EkA
又EkA=8 J,得EkB=32 J.
(3)物体从A→M,设小球所受的电场力为F,在水平和竖直方向分别运用动能定理的“分解式”,有
Fx1=EkMx-EkAx
(7)
-Gh=EkMy-EkAy
(8)
其中EkAx=0,EkMy=0,得
Fx1=6 JGh=8 J
又
(9)
(10)
由式(7)~(10)得
由图9可知
设电场力和重力的合力为
F合=mg′=G′
式中G′为等效重力,以G′所在方向为轴建立直角坐标系,如图9所示.

图9 等效重力场
在小球从A到B的过程中,将速度分解至坐标轴上,当小球在沿G′方向的分速度减为零时,具最小速度为
vmin=v0sinθ
又
且
得

