基于Phyphox软件定量探究圆周运动各量间的关系
郭家丰 唐兴华
(厦门实验中学 福建 厦门 361026)
1 引言
在高中物理必修二探究影响向心力大小的因素时,我们使用了控制变量法,借助向心力演示仪(图1)探究出向心力与质量成正比,与角速度的平方成正比,与半径成正比.在国际制单位下,我们和学生说明关系式F∝mω2r中,比例系数为1,得到F=mω2r.但在验证的过程当中缺少了定量推导,让学生直观看到向心力的确是等于三者的乘积.我们可以由牛顿第二定律得到:F=ma,那么向心力与物体的质量和向心加速度成正比,我们只要得到向心加速度和角速度以及半径的定量关系就可以验证向心力与三者之间的定量关系.

图1 向心力演示
为了利用Phyphox软件实现定量分析,教师可以带领同学们自制实验仪器,培养学生们的科学核心素养.
2 实验原理和实验仪器的制作
本文通过牛顿第二定律得到,向心力与物体质量和向心加速度成正比,那么我们可以通过探究向心加速度与角速度、半径的定量关系得到向心力与质量、角速度、半径三者之间的定量关系.
Phyphox软件是利用手机上内置的传感器进行物理数据测量的一款APP(图2),该软件可以准确地测量出手机实时的向心加速度和手机转动的角速度,并作出a-t图和ω-t图,并将a和ω的关系拟合在同一个坐标系中.最后我们可以通过软件导出数据进行定量分析.
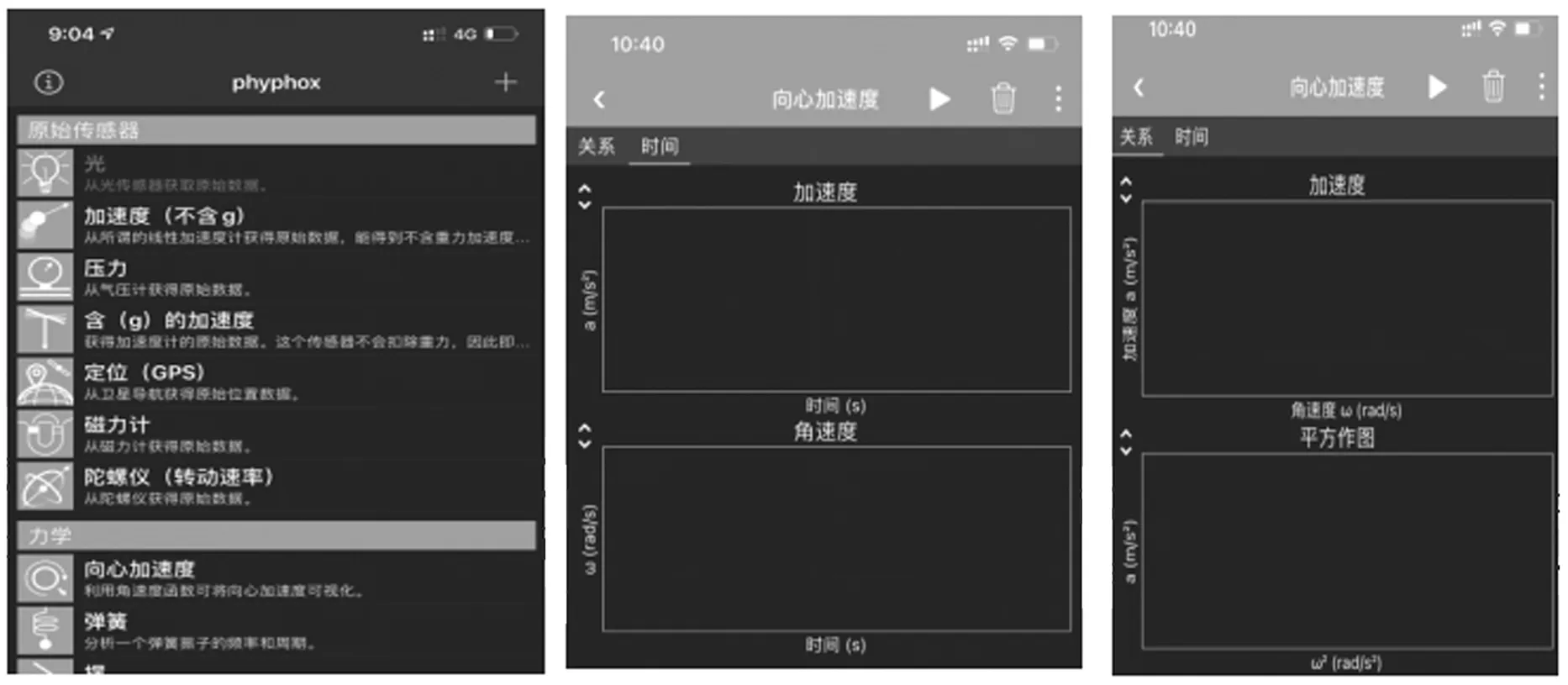
图2 Phyphox软件
实验道具需满足带动手机做圆周运动的本领,同学们想到了用硬塑料做一个圆盘,并在圆盘上面做卡槽,可以将手机放在上面.将圆盘固定到电机上,电机(图3左)带动圆盘做匀速圆周运动.我们可以利用调速器(图3右)控制圆盘转动的角速度大小,利用自制的手机支架(图4)尺寸在圆盘上制作的卡槽(图5)来改变手机做圆周运动的半径.由于电机带动圆盘会产生一定的晃动,我们将电机嵌入到一个泡沫箱里,防止它因转动产生的震动(图6).

图3 调速器

图4 手机支架

图5 圆盘(卡槽)

图6 泡沫箱
3 向心加速度的定性探究
3.1 探究一:向心加速度与角速度的关系——控制半径不变
将手机支架插在半径15 cm卡槽处保持不变,并利用希沃投屏软件将手机屏幕投放在多媒体上,实时观测实验数据变化.调速器调至第1挡,打开开关;我们可以从屏幕中实时监测向心加速度和角速度随时间的变化情况(图7).当转速稳定后20 s左右时间,继续调速,将调速器分别调至第2挡至第6挡.实验结束后关闭调速器开关.

图7 探究向心加速度与角速度的关系
从图中我们可以观察到实验结果,随着角速度的不断增大,向心加速度也在随之不断地增大,并且在对应的角速度下保持稳定不变.那么利用软件将向心加速度和角速度进行拟合,如图8所示,可以看到加速度随角速度变化是非线性关系.由于图像很象一条抛物线,所以我们将角速度平方,来探究a和ω2的关系.得到图8.可以很明显地看到图像是一条经过原点的正比例图线.
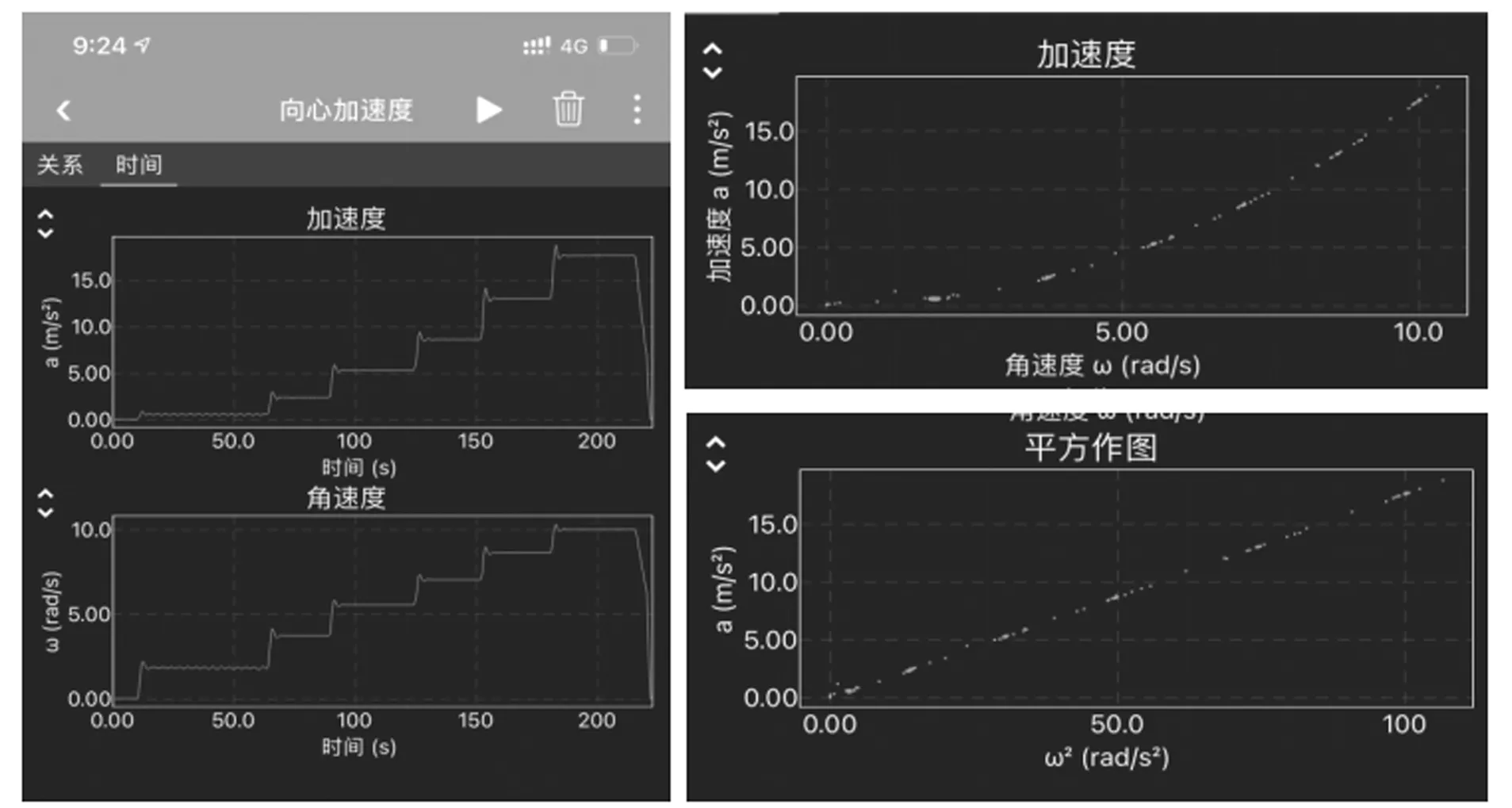
图8 向心加速度与角速度
结论一:向心加速度与角速度的平方成正比,即a∝ω2
3.2 探究二:向心加速度与半径的关系——控制角速度不变
将调速器固定到4挡的位置并在整个实验过程中不可触碰挡位.手机支架先插在半径10 cm卡槽处,并利用希沃投屏软件将手机屏幕投放在多媒体上,实时观测实验数据变化.打开开关,我们可以从屏幕中实时监测向心加速度和角速度随时间的变化情况(图9).

图9 探究向心加速度与半径的关系
当转速稳定后一段时间,我们关闭开关,将半径增大(从刚才的10 cm分别增大至15 cm,20 cm,25 cm)后,待稳定一段时间后直接断开开关.
我们可以从APP中的ω-t图[图10(a)]发现在每次改变半径的过程当中,由于调速器挡位固定,圆盘稳定后角速度一直都是一个定值.但随着每次半径的增大,向心加速度也在随之增大,我们将数据导出,将半径作为横坐标,向心加速度作为纵坐标,利用excel建立直角坐标系并可以从图像中看到4个清晰的点(半径在变大的时候,由于圆盘晃动导致向心加速度的数值变化范围较大,数据点有点细长),将4个点拟合后发现他们处于经过坐标原点的同一条直线上[图10(b)],非常完美地验证了向心加速度与半径成正比.

(a)ω-t的关系
结论二:向心加速度与角速度的平方成正比,即a∝ω2
我们可以得到:向心加速度与角速度平方和半径成正比,即,a∝ω2r.那么他们之间的比例关系如何呢?接下来,我们通过APP导出实验数据,验证他们之间的比例关系.
4 向心加速度的定量探究
4.1 定量探究——向心加速度与角速度的关系
我们将探究一中的实验数据从手机软件当中导出,phyphox软件平均0.5s时间记录一次数据,我们将每个挡位下的数据进行平均值,得到6个挡位下的6组数据.如表1所示.
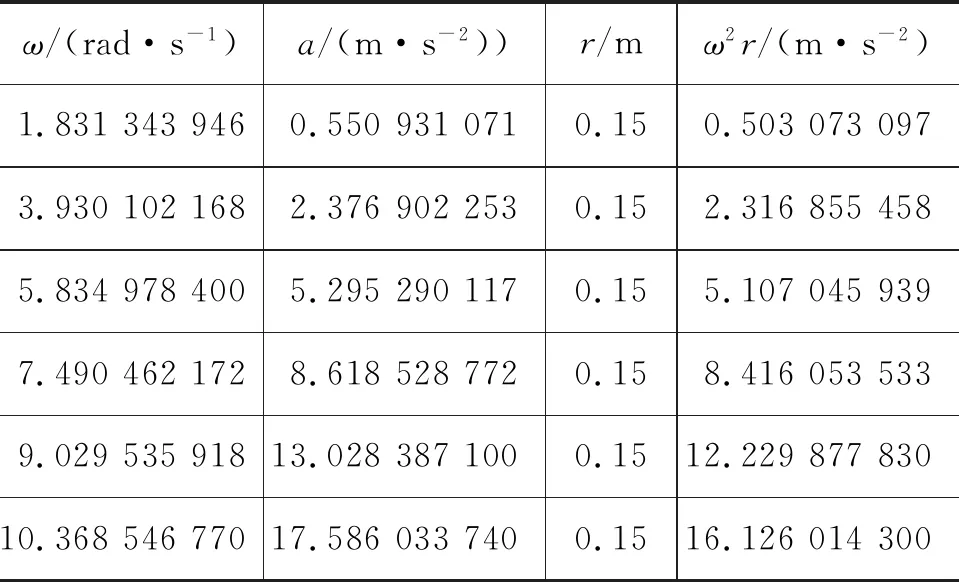
表1 半径不变,向心加速度与角速度的定量关系
第一列表示角速度,第二列表示向心加速度,第三列表示圆周运动半径,最后一列是ω2r的值.我们可以从图中看到误差允许范围内,实际测得的加速度与ω2r的值是相等的.
4.2 定量探究——向心加速度与半径的关系
我们将探究二中的实验数据从手机软件当中导出,如表2所示.
从表2我们可以看到当保持角速度不变的时候,向心加速度大小随着半径的增大而增大,我们通过计算 发现,在误差允许的范围内, 的数值和手机直接测得的向心加速度大小保持一致.

表2 角速度不变,向心加速度与半径的关系
以上两组探究实验的数据说明,在国际制单位下,向心加速度等于角速度的平方乘以半径,即
a=ω2r
5 误差分析
(1)由于实验器材是由教师和学生独立制作完成,电机固定在泡沫纸箱里并不能保证电机完全稳定,会轻微晃动.
(2)圆盘选用硬塑料在淘宝定制,在后期实验中,由于手机的压力作用,圆盘不是很平整,导致角速度和半径不变的基础上,手机测得的向心加速度不是一个定值,但在一个很小的范围内波动.
(3)圆盘上的卡槽是根据盛放手机的支架决定的,半径是人工测量并在制作时打孔,可能会出现一定误差.
(4)当保持半径不变时,我们可以通过比较实验测得的向心加速度数据和通过计算得到的ω2r的数值,计算发现误差仅为2%~8%之间;当保持角速度不变时,比较通过实验测得的向心加速度数据和通过计算得到的ω2r的数值,计算发现误差仅为2%~7%之间.
6 总结
本文是笔者在开一节区级公开课前翻阅文献,看到文献[2]“向心力演示装置的设计与制作”,内心产生的一个实验想法.并且也看到了文献[3]设计的教具.和学生一起探讨后,大致确定了整个实验需要的一些器材,就带着他们一起去学校旁边的建材市场购买了.在购买的过程当中,和比较专业的师傅探讨了很多问题,在后续制作实验装置过程中也遇到了很多问题,并且在大家一起努力下,最终克服困难制作好了这一实验装置,并且实验结果相对比较精准.
本文没有直接探究向心力与质量、角速度和半径三者之间的关系,而是先利用牛顿第二定律告诉大家,每一个力都可以产生一个加速度,并且所需外力与质量和加速度分别成正比,即m一定时,F∝a,而a一定时,则有F∝m,这就是三者的关系.在实验前引出了向心加速度的概念,接下来就开始猜想并通过本文的实验来定性和定量地验证向心力公式.Seewo软件是近几年非常流行的一个教学软件,投屏功能非常稳定,这也为我们的整个实验提供了非常好的辅助措施.手机在做圆周运动的过程中,我们无法观看手机屏幕,来实时监测实验数据,但是Seewo投屏功能为我们解决了这一难题,我们可以在教室的多媒体上很清楚地看到向心加速度、角速度随时间的变化情况.
最后,该实验装置的整体原理较为简单,在如今高速发展的工业时代,想要实现一些设想非常容易.本文在探究向心加速度与哪些因素有关的同时,也引导学生主动设计、猜想并通过自己的努力实现探究的目标.很好地培养了学生的科学核心素养.同时,也在激励着笔者不断地学习与进步,更好地成就学生和自我.

