一种串/并混合的多输入多输出信号检测算法
赵壮志, 侯 嘉,2*
(1.苏州大学电子信息学院, 苏州 215000; 2.电子科技大学长三角研究院(衢州), 衢州 324000)
近几十年来,无线通信领域在飞速变化发展,无线通信数据量的激增导致频谱资源的短缺[1]。为了合理有效地利用频谱资源,多输入多输出(multiple-input multiple-output, MIMO)技术应运而生[2]。MIMO技术在收发两端同时使用多根天线,在不增加带宽和发射功率的条件下成倍地提高了系统容量和频谱效率[3]。MIMO技术带来增益的同时,也带来了新的问题。随着天线数量的增加,检测算法的复杂度也在呈指数级的增加。在实际应用中高复杂度的检测算法需要消耗更多的硬件和能量资源,因此研究低复杂度高性能检测算法就显得十分必要了。
在MIMO系统中,最优信号检测算法是最大似然(maximum likelihood, ML)算法[4-5],但其复杂度随天线数目的增加呈指数形式增长。次优检测算法则包括线性检测算法、并行干扰消除(parallel interference cancellation, PIC)和串行干扰消除(successive interference cancellation, SIC)等。其中线性检测算法,如迫零(zero forcing, ZF)检测算法复杂度较低[6-9],但检测性能较ML算法相差甚远。与线性检测算法相比,PIC和SIC是在结合线性检测结果的同时,引入了迭代消除思想来进一步优化线性检测的结果,其复杂度较高[10-14],但相对的性能也较好。在PIC和SIC检测算法的基础上进行融合研究,希望在降低算法复杂度的同时提高算法的检测性能。
1 系统模型
假设单用户MIMO系统模型如图1所示,其中发射端天线数量为Nt,接收端天线数量为Nr,且有Nt=Nr=N,N为天线数目。

图1 MIMO系统模型Fig.1 MIMO system model

信道矩阵H为N×N方阵,是零均值单位方差的平坦瑞利衰落信道。
(1)


y=Hs+n=h1s1+h2s2+…+hNsN+n
(2)
2 基于PIC的计算优化
2.1 并行干扰消除检测算法
PIC检测算法首先由前置检测器获得相对不太精准的信号估计,如果前置检测器为ZF,则为ZF-PIC,其前置检测的输出估计信号可表示为
(3)
式(3)中:DEQM(·)表示对(·)信号根据M阶QAM星座图进行硬判决后的输出估计结果。
PIC算法则是以并行计算每一个符号减去前置估计结果的方式进行迭代更新计算,可表示为

(4)
(5)
式(4)和式(5)可以并行执行,因而检测速度有所提高。算法复杂度方面,PIC检测主要集中在式(4)中信道矩阵和前置检测估计结果相乘部分。
2.2 基于PIC检测的优化计算
由式(4)可知,PIC的并行计算还可表示为
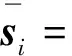
(6)
2.3 混合干扰消除检测算法
考虑融合SIC的思想,将某一路或几路PIC计算的估计结果应用到其他PIC计算估计中,使得PIC与SIC相结合,这就形成了混合干扰消除(hybrid interference cancellation, HIC)检测模型。以4×4 MIMO系统为例,介绍两种类型的HIC检测模型,其中Ⅰ型为在并行中串行,其检测模型如图3所示;Ⅱ型为先并行再串行,其检测模型如图4所示。


图2 基于PIC检测的优化计算模型Fig.2 Optimized calculation model based on PIC detection
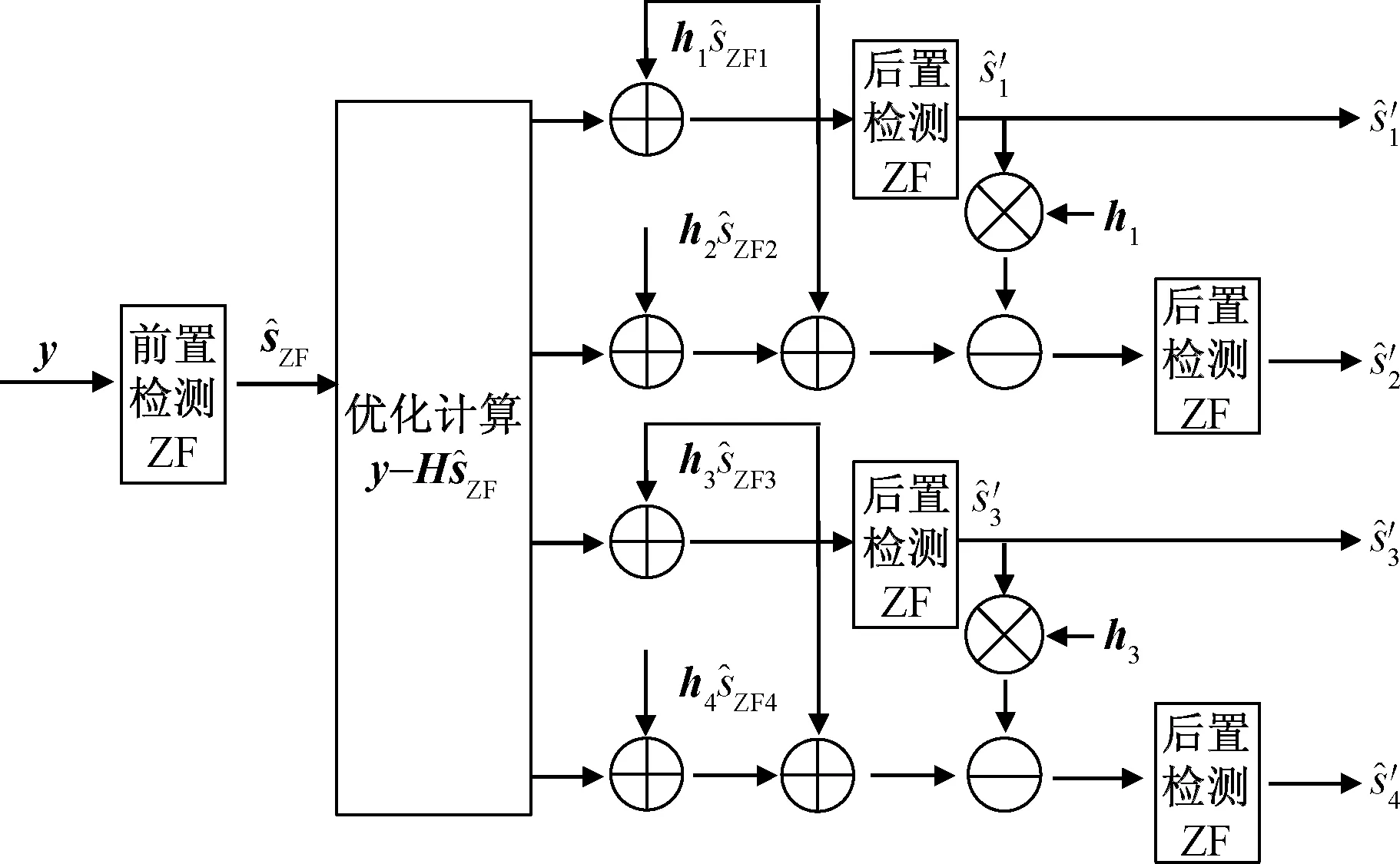
图3 Ⅰ型HIC检测模型Fig.3 Type Ⅰ HIC detection model

图4 Ⅱ型HIC检测模型Fig.4 Type Ⅱ HIC detection model

(7)
(8)
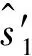
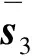
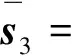
(9)

(10)
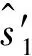
3 仿真结果与分析
3.1 算法复杂度分析
首先,表1给出了传统PIC算法与优化计算后的PIC算法的复数乘法数目的对比结果,很明显通过提出PIC计算中的相同部分进行优化可以很好地降低计算复杂度,且随着天线数目N的增加,复杂度的降低更为明显。而4N2+2N的复数乘法复杂度,使得所提的优化计算PIC算法也有了应用在大规模MIMO系统的可能。
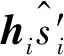
以ZF-HIC算法为例,在16×16MIMO系统下不同串/并组合选择下的复数乘法复杂度对比结果如表2所示。可以看出,两种HIC检测模型在相同串/并组合选择下的复数乘法复杂度相同。
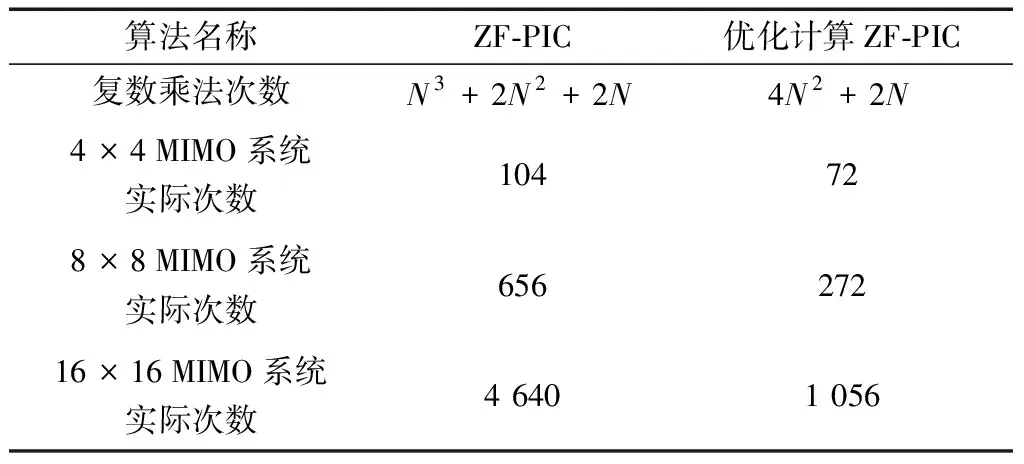
表1 PIC与优化计算PIC的复杂度Table 1 The complexity of PIC and optimized calculation PIC
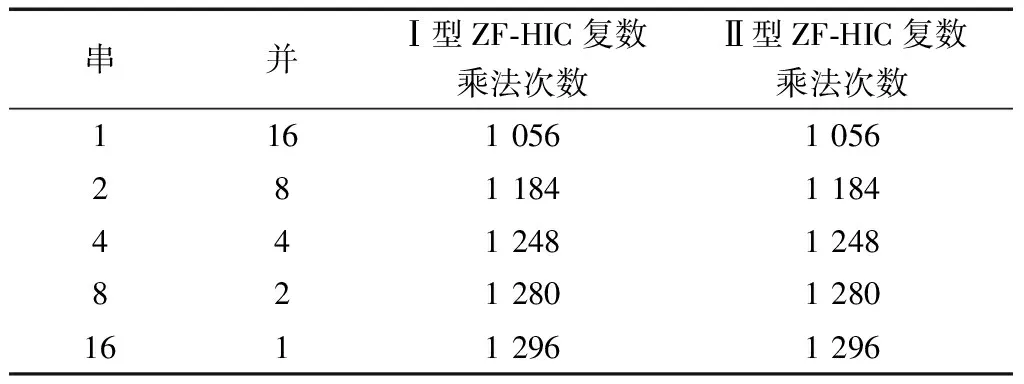
表2 16×16系统HIC不同串/并选择下的复杂度Table 2 The complexity of HIC under different serial and parallel choices in 16×16 system
特别指出的是当HIC算法采用1串N并时,其实就是优化计算PIC算法,其复数乘法复杂度和性能与其相同。HIC算法的复数乘法复杂度和性能都会随着串行数目的增加而增加。然而即使HIC算法采用N串1并时,其复杂度较传统PIC算法依然有量级的提升。
3.2 仿真结果
实验验证所提出的优化检测算法的可靠性主要通过传输误比特率性能来进行描述,误比特率越低则传输可靠性越高。在相同的平坦瑞利信道仿真条件下,2.3节提到的两种HIC检测模型在4-QAM调制的4×4 MIMO系统中,都采用2串2并选择的传输误比特率性能对比结果如图5(a)所示。可以看出,在同为2串2并的情况下,误比特率为10-5时Ⅱ型HIC检测模型较Ⅰ型HIC检测模型大约有0.1 dB的性能优势。这是因为在相同串并选择的情况下,Ⅱ型HIC检测模型对信号估计的利用率更高,误差传播的概率小。
如果提高天线数目,两种HIC检测模型在4-QAM调制的16×16 MIMO系统下,都采用4串4并选择的传输误比特率性能对比结果如图5(b)所示。可以看出,在同为4串4并的情况下,误比特率为10-5时Ⅱ型HIC检测模型较Ⅰ型HIC检测模型大约有0.6 dB的性能优势。图5(a)和图5(b)对比可知,随着系统规模和天线数目的提升,两种HIC检测模型的差异也会变明显,Ⅱ型HIC检测模型的传输误比特率性能会更好,虽然复数乘法数目不变,但是串行时延会增加。
以性能较好的Ⅱ型HIC检测模型为例来与传统的ZF-PIC算法进行比较分析。在相同的信道仿真条件下,采用4-QAM调制的4×4、8×8、16×16MIMO系统的传输误比特率性能仿真结果如图6所示,其中HIC算法采用的串并选择都是N串1并。从图6(a)可以看出,4-QAM调制的4×4MIMO系统中 ZF-HIC算法在误比特率为10-5时较ZF-PIC算法有大约0.3 dB的性能提升;从图6(b)可以看出,4-QAM调制的8×8MIMO系统中ZF-HIC算法在误比特率为10-5时较ZF-PIC算法有大约0.8 dB的性能提升;图6(c)可以看出,4-QAM调制的16×16MIMO系统中ZF-HIC算法在误比特率为10-5时较ZF-PIC算法有约1.2 dB的性能提升。对比图6(a)、图6(b)、图6(c)可知,对于规模越大的系统,所提的HIC算法较PIC算法性能优势越明显。这是因为系统规模越大,所提HIC算法每个子检测平均使用的新估计数量越多因而误差传播的概率越小。

图6 HIC误比特率仿真结果Fig.6 Simulation results of bit error rate of HIC
4 结论
(1)主要介绍了一种基于PIC算法的串/并混合MIMO系统检测算法。所提算法能有效地在降低计算复杂度的同时提高检测性能。
(2)主要的改进思路为提取出PIC计算过程中的共同部分来优化计算过程,降低了整体检测系统的复数乘法数目的量级,因而后续可以将其应用到大规模MIMO的检测算法中;融入SIC思想提出了HIC检测模型架构,在低计算复杂度的前提下,提高了检测性能,而且HIC 对比传统PIC算法的性能优势会随着系统规模和天线数目的提升变得更加明显。

