高维中介分析方法及其在组学研究中的应用*
魏梦珂 周广帅 范冰冰 吕嘉丽 张 涛△
中介分析在生物医学、行为和社会科学研究中扮演着重要的角色,主要用来研究自变量和因变量之间的内部作用机制。经典的中介分析是针对单个中介变量的研究,近年来,对于多元中介模型的研究也有一定的发展。随着高通量检测仪器和技术的发展,高维数据在许多科学领域变得越来越普遍,由于高维数据的特点(n 中介分析的基本模型见图1(a),用Ai表示个体的暴露,其中,Ai=a(Ai=a′)表示个体暴露(未暴露)于某一研究因素,Mi表示中介变量,Yi为结果变量。传统的中介分析要求研究变量为连续变量,且自变量和中介变量之间无交互作用,而实际研究数据往往难以满足,限制了中介分析的应用。Jo[1]和Sobel[2]提出了基于反事实理论的因果中介分析方法,该方法对研究变量的类型没有限制,在一定程度上丰富了中介分析的应用。 图1 中介分析的路径模型 同时,在A和M无交互作用的情况下,按照效应分解的原理可以将暴露A由a变为a′时对结果的总效应(total effect,TE)分解为自然间接效应(natural indirect effect,NIE)和自然直接效应(natural direct effect,NDE),表示为:TE=NDE+NIE。利用潜在结果符号,可以将三种效应定义为[4]: NIE≡E[Yi(a,Mi(a))-Yi(a,Mi(a′))] NDE≡E[Yi(a,Mi(a))-Yi(a′,Mi(a))] TE≡E[Yi(a,Mi(a))-Yi(a′,Mi(a′))] 根据图1(a)对中介变量和结果变量建模: (1) (2) 模型(1)中,αC为协变量C对M的效应系数,αA为暴露A对M的效应系数,εM为残差项;模型(2)中,βC为协变量C对Y的效应系数,βA为暴露A对Y的直接效应系数,βM为M对Y的效应系数,εY为残差项。暴露通过中介变量对结果的间接效应可以表示为αAβM,暴露对结果的直接效应可以表示为βA,结合反事实理论可以将NIE和NDE定义为: NIE=(a-a′)αAβM NDE=(a-a′)βA 高维中介分析方法主要有两种:一种是基于线性结构方程模型(linear structural equation model,LSEM)惩罚的方法;另一种是基于主成分分析(principal components analysis,PCA)进行降维的方法。此两种方法都需要对中介变量和结果变量分别拟合模型。图2为高维中介的一般模型,Ai表示个体的暴露;p维可能的中介变量Mij={Mi1,Mi2,…,Mip}(j=1,…,p),也可以表示为Mi(a)={Mi1(a),Mi2(a),…,Mip(a)},均为连续变量;Yi为结果变量,也为连续变量。εMij和εYi分别是中介变量Mij和结果变量Yi的残差项。需要注意的是实际研究中还应该考虑中介变量之间的关联。 图2 高维中介分析模型 因果中介分析的SUTVA、正值假设和各项混杂假设同样适用于高维中介分析,且假设④在多元中介模型中较易实现[5]。用C表示q个观测到的混杂变量,则可对每个研究对象拟合因变量模型(若因变量为二分类变量,则建立logistic回归模型): (3) 其中,βC=(βC1,…,βCq)T为协变量C对Y的效应系数;βM=(βM1,…,βMp)T为p个M对Y的效应系数;βAM=(βAM1,…,βAMp)T为暴露与中介变量之间的交互项系数集合。大多数研究中假设暴露与中介变量之间没有交互作用,因此为后续的描述方便,本文假设该项不存在。一般认为残差项εYi服从均数为0,方差为σ2的正态分布。可以看出该结果模型纳入了所有的候选中介变量,这相对于建立多个单中介模型有如下优点:只建立一个模型,提高了检验效率;同时校正了其他的中介变量,考虑了中介变量之间的相关性,减少偏倚;可以评价特定间接效应的大小。 (4) Mi=(αAi⊕hiCi1⊕…⊕hqCiq)⊕εMi hi对应于协变量Ci,βM1k=0,1k为k个1的向量。 NDE:E[Yi(a,Mi(a′))-Yi(a′,Mi(a′))|Ci]=βA(a-a′) 这时候,他们的头顶上已经传来鲲鼓翼的声音。他们抬头去看,宇晴师父坐在鹏背上,向他们俯冲过来,李离、上官星雨、袁安三人双足往山路上一点,衣袂飘飘,身形如箭,向鲲鹏的翅背间跳丸飞弹般射来。正是宇晴指点他们练成的“点墨山河”击水兮万里,纵翼兮排云,轻功之俊赏,与当日宇晴在黄梁驿见到时,已经是天差地别,宇晴不由得心里一暖。 Zhao[16]和Chen[7]在利用近似弹性网和岭回归的基础上也加入了增广拉格朗日函数来增强约束条件: 值得注意的是,以上方法多是对回归系数进行惩罚估计,而Zhao[16]的研究中同时对间接效应αAjβMj进行了惩罚。 目前文献对高维中介效应的检验主要分为两种:一种是分别检验回归系数αA和βM;另一种是对乘积项αAβM的直接检验。对于成分数据的中介效应检验和基于PCA分析的方法,都包括整体中介效应(overall mediation effect,OME)检验和单组分中介效应(component-wise mediation effect,CME)检验两部分,其检验方法基本是相同的,都是对乘积项αAβM的直接检验。 1.回归系数检验法 (1)逐步法检验(Baron and Kenny):多用于对单中介模型的回归系数进行检验,即首先检验A对Y的总效应,若有统计学意义,再进行后续检验;然后回归系数αAj和βMj,二者均有统计学意义则认为中介效应存在;最后检验回归系数βAj,判断中介效应是完全中介还是部分中介。这种方法由于其为大众熟知的对总效应的限制及要求数据满足正态分布的局限性,导致其检验效能较低。而且对于高维数据来说计算量很大,且未考虑中介变量之间的共线性,并不适用。 2.乘积项检验法: (4)贝叶斯后验概率法:首先用马尔科夫链蒙特卡罗(MCMC)中的Hastings-within-Gibbs算法获得联合log后验分布的样本;然后对每一个中介变量估计在有较大方差的正态分量中βM和αA的后验概率P(rmj=1,raj=1|Data),作为后验包含概率(the posterior inclusion probability),来评估贝叶斯变量选择方法的中介效应。rmj和raj是引入的指示βM和αA来源的变量。 ① 将自变量和因变量打乱,随机抽取置换检验的样本:A(b)和Y(b),b=1,…,B; ④ 得到P值: 该方法对总体分布的要求较自由,应用较为广泛。 近年来,随着高通量检测技术和统计学方法的发展,医学研究中的高维组学大数据(如基因组学、转录组学、表观遗传学、代谢组学、微生物学等)呈海量增长。中介分析在疾病的病因推断中有重要作用,可以打开系统流行病学的黑盒子,为疾病的机制研究、防治干预提供依据。然而由于高维组学数据具有变量多、稀疏、共线性等特点,基于单变量的中介分析方法已经不适用于这类数据,故多位研究者对高维数据的中介分析方法进行了探索。综合各项研究可以发现今后对于高维中介分析的研究趋势有以下几点: 1.模型发展方面,将所有的中介变量纳入因变量模型是大家的共识,然后对其建立LSEM,然而对于成分数据,还需要发展更合适的模型;而且大多数研究假设暴露和中介变量之间无交互,因此模型中是否纳入交互项也需要进一步探索。 2.效应估计方面,目前对于效应系数的估计主要是基于Lasso正则化及扩展的方法,但由于Lasso估计有偏、不满足Oracle性质的缺点,还需要发展更加合适的方法来筛选中介变量。 3.中介效应的检验方法,目前bootstrap和蒙特卡罗的检验方法应用较多,随机森林和贝叶斯网络的方法可能是未来的发展方向。 4.中介变量的解释问题,对于成分数据和利用PCA进行降维的中介分析,多是发现一组有中介效应的变量,这对于成分数据较为合适,但是对于为了发现特定中介路径的研究来说,解释较为困难。 5.敏感性分析,高维中介分析是在SUTVA和四项混杂假设的基础上进行的,由于真实数据多无法满足这些假设,故需要进行敏感性分析,而目前只有Sohn[11]进行了敏感性分析,故对于敏感性分析方法的探索也可能是未来的研究方向。 6.高维数据中协变量的选择方法研究还不够深入,对于潜变量的高维中介分析方法同样需要进一步研究[23],而且随着高维纵向数据的增多,也对高维中介分析提出了新的挑战。因果中介分析模型
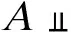
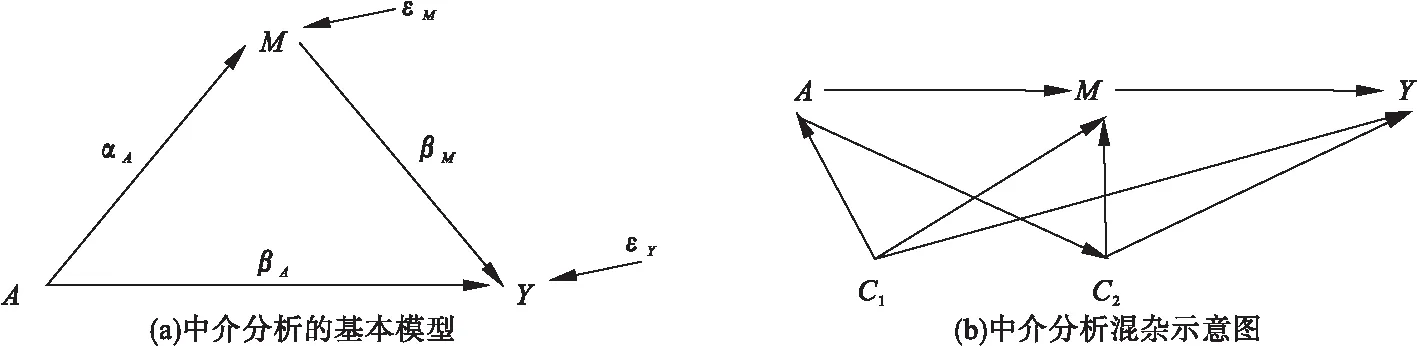
高维中介分析模型
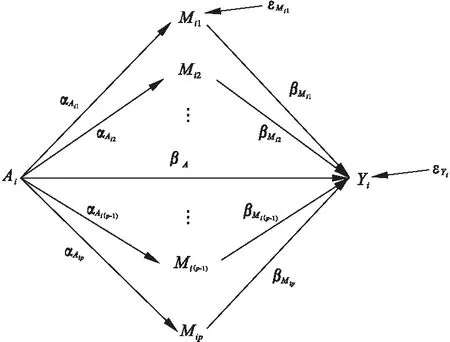

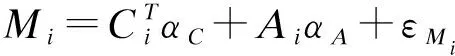


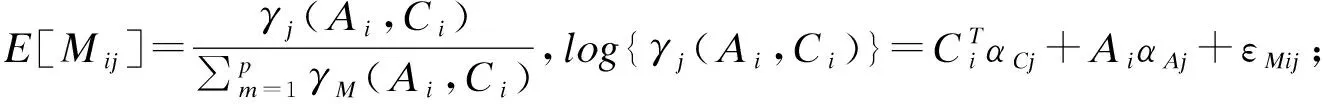
高维中介分析效应估计
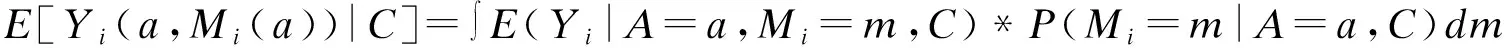
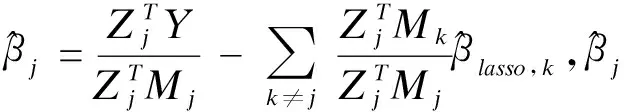

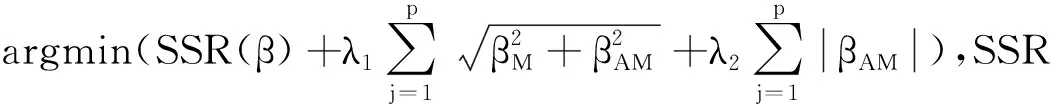


高维中介分析效应检验
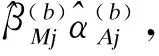
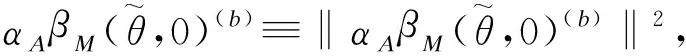
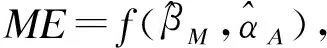

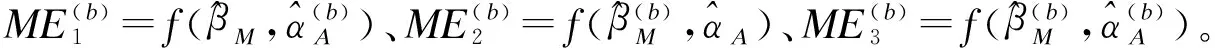
小结与展望

