基于贝叶斯方法研究DNA甲基化在儿童经历虐待与成年罹患抑郁障碍间的中介效应

黄 煜 孙翔飞

【提 要】 目的 识别介导儿童期经历中等至极端虐待与抑郁障碍相关的DNA甲基化位点，有助于在分子水平阐明抑郁障碍的发病机制，同时也可为改善临床治疗手段提供参考依据。方法 采用基于贝叶斯压缩估计的高维中介效应模型识别具有中介效应的DNA甲基化位点，数据来源于gene expression omnibus(GEO)数据库，分析采用基于R4.0的hdbm包进行分析。结果 采用贝叶斯高维中介效应模型进行分析，研究识别出具有潜在中介效应的2个DNA甲基化位点，分别为cg08522473与cg13224723，且分别位于基因TAGLN3与PAOX。结论 采用该模型识别出的甲基化位点分别位于基因TAGLN3与PAOX，且该基因都在人脑中有表达，且都与人类精神疾病相关，故这些DNA甲基化位点很可能介导了儿童期经历中等至极端虐待后导致成年抑郁障碍的发生。

抑郁障碍是最常见的精神障碍之一，是指各种原因引起的以显著而持久的心境低落为主要临床特征的一类心境障碍。据WHO报告的数据显示，全球有超过3.5亿人受到抑郁症的困扰，且在近十年来罹患该疾病的人数增长了约18%，故阐明抑郁障碍的发病机制具有重要的意义。目前普遍认为抑郁障碍发病是遗传、心理、社会环境等多种因素共同作用的结果。近年来越来越多的研究者在表观遗传学领域对该疾病的发病机制进行了研究，且有研究表明DNA甲基化与抑郁障碍的发病存在关联[1]。DNA甲基化是基因表观遗传修饰机制的一种，它虽不会改变DNA序列，但却能影响DNA序列的活性，从而产生一些未知的生物学效应。

目前有研究支持儿童期遭受虐待会增加成年后罹患抑郁障碍的风险[2-3]。但是在分子水平上对该疾病的发病机制却未完全阐明，有研究表明DNA甲基化可能参与了该疾病发病。目前的研究可知，儿童期经历过虐待可导致DNA甲基化[4]，此外，也有研究支持DNA甲基化与成年罹患抑郁障碍有关[1，5]，识别DNA甲基化位点对于在分子水平层面阐明抑郁障碍征具有重要的意义。

DNA甲基化在抑郁障碍的发病过程中起的作用相当于“黑盒”效应，即儿童期经历虐待导致DNA甲基化的改变，DNA甲基化的改变又导致罹患抑郁障碍。DNA甲基化发挥着介导的作用，且可以建立起抑郁障碍的发病过程。

中介效应分析是研究中介变量如何解释暴露变量影响结局的机制。中介效应分析可将暴露变量对结局的作用分为两部分：通过中介变量发挥的作用称为中介效应；中介变量无法解释的效应则称为直接效应。在我国医学研究领域涉及中介效应的研究中多为中介模型的应用[6-8]。较少涉及中介模型的方法学研究。目前的中介分析方法由单中介模型，进阶为多中介模型，以及高维中介模型[9-10]，此外，这些模型适用于连续和二分类结局，同时也有研究考虑暴露与中介变量间的相互作用的研究[11]。但是，这些研究基本都忽略了中介变量间的关系，由于DNA甲基化数据存在高维的特性，以及测序技术的原因，不可避免地在位点间存在一定的相关性。

基于以上的考虑，本研究采用高维情况下的贝叶斯中介分析方法[12]。贝叶斯中介模型是在分层框架中提出的，在该理论框架中，暴露因素对结局的影响是基于单个中介变量定义的。为了估计模型中的直接和中介效应，我们做了中介效应稀疏性的假设，即认为在只存在少部分的中介变量具有中介效应。在该先验下，认为一小部分的DNA甲基化位点介导了儿童期经历中等至极端虐待对成年后罹患抑郁障碍的效应。该方法将DNA甲基化位点识别的问题转变为DNA甲基化位点的选择问题，并应用贝叶斯方法对连续收缩率的影响进行预测。该方法不仅可以同时分析多个中介变量，而且也无需对中介变量做出任何路径特定或因果顺序的假设。

资料与方法

1.数据来源

研究数据来自于美国格雷迪创伤项目研究，该研究在获得埃默里大学医学院和格雷迪纪念医院机构审查委员会批准后，将亚特兰大市中心居民中招募的非裔美国人作为研究对象。该数据集包含基线信息、细胞组成资料和DNA甲基化数据(DNAm)。研究采用改良的贝克抑郁量表(BDI)对研究对象进行测量[13]，且筛选出BDI评分≥10的观察单位。在观察结果中，排除了接受过抑郁障碍治疗的研究对象，因为接受的治疗可能会影响DNAm的改变，从而使中介效应分析的结果变得更为复杂与不确定。同时，研究也剔除了儿童期经历中度至极端虐待缺失的观察单位，最后纳入中介效应分析的研究对象有128例。关于该研究项目的详细信息，读者可以在网站http：//gradytraumaproject.com/进行参阅。研究采用的原始数据(DNAm数据、临床数据和细胞数据)可以在以下网址进行下载获取 https：//www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE72680。

2.方法

本研究采用R4.0软件的hdbm包进行分析，利用实际数据构建两个条件回归模型，在利用Yi|Ai，Mi，Ci模型时，要确保暴露因素Ai与Yi之间有关联。首先构建Yi|Ai，Ci模型：

(1)

继而再构建Yi|Ai，Mi，Ci模型：

(2)

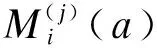
其次，构建Mi|Ai，Ci模型，即

Mi=Aiαa+αcCi+εMi

(3)

DE=E[Yi(a，Mi(a*))-Yi(a*，Mi(a*))|Ci]=βa(a-a*)

中介效应可表示为：

ME=E[Yi(a，Mi(a))-Yi(a，Mi(a*))|Ci]=

(1)贝叶斯方法先验的指定

本研究对于第j个中介因素，假定了两个正态分布的先验，即

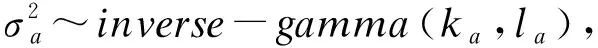
(2)后验抽样算法

结 果

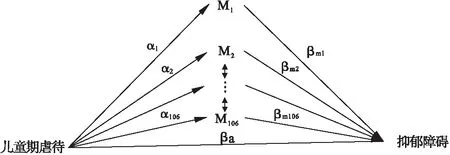
图1 具有最大效应的106个DNA甲基化位点介导的儿童期经历虐待导致成年罹患抑郁障碍

(4)

表1 贝叶斯高维中介模型识别出具有中介效应的甲基化位点

讨 论

本研究采用贝叶斯高维中介模型识别出了介导抑郁障碍发病的潜在中介效应基因TAGLN3与PAOX。图2反映出基因TAGLN3在人脑中高表达，在人体的其他组织中则为呈低表达状态，且Aguzzi等在2008研究发现该基因编码蛋白hNP25，且该蛋白能够上调与增强调节克罗伊茨费尔特-雅各布病与维持细胞骨架功能间的关系，该疾病是由朊病毒引起的中枢神经系统变性疾病[19]。则说明该基因参与了某些神经系统疾病的发病。虽然未发现直接的研究支持该基因与抑郁障碍有关，但是认为该基因很可能与抑郁障碍的发病过程有关。对于基因PAOX，图3反映出该基因在人脑中并非呈高表达状态，但是目前的研究发现，基因PAOX与某些精神疾病相关，比如，Moore K等研究发现基因PAOX对于焦虑的发病能起到保护作用；Cabrera-Mendoza B等对人脑基因甲基化与自杀身亡进行了研究，提出基因PAOX是在以后的自杀研究中值得研究的基因[20]，同样未找到直接的研究支持基因PAOX与抑郁障碍的发病有关，但是抑郁障碍与自杀存在很高的相关性，故该基因有很大可能性介导了儿童期经历中等至极端虐待导致成年后抑郁障碍的发病。研究结果可为分子水平上阐明抑郁障碍的发病机制提供参考，但要得出确定性的结论，则需要进行生物学实验才能验证。

图2 基因TAGLN3在不同人体组织中的表达量，该图来自于(https：//www.ncbi.nlm.nih.gov/gene/29114)

图3 基因PAOX在不同人体组织中的表达量，该图来自于(https：//www.ncbi.nlm.nih.gov/gene/196743)

本研究虽采用了Song等研究提出的模型，同时也进行了数值模拟研究佐证了该方法的优越性。但是，利用该模型进行分析时，未对甲基化位点的性质进行考量，位于不同基因的DNAm位点，由于基因间可能存在着上位效应，即DNAm位点在发挥效应时，可能处于不同的水平。而该模型将所有的DNAm位点都视为在同一水平发挥效应；该研究基于DNAm位点进行研究，但基因才是遗传的基本功能单位，对甲基化位点的生物学解释具有一定的局限性；其次，研究识别出与抑郁障碍相关的DNAm位点在不同人群或地区中可能具有一定的差异性，因为甲基化位点较基因的稳定性差，故结果的外推性小；同时，模型在计算中介效应时采用了平方的形式来避免不同方向中介效应的相互抵消，但是位点在模型拟合的过程中，无法控制方向不同的中介效应的相互抵消，致使可能无法识别出具有潜在中介效应但存在相互抵消的位点。同时，识别出具有潜在中介效应的位点的意义要远大于计算出中介效应大小的意义，计算中介效应的大小的目的是要了解在抑郁障碍发病过程中中介效应所占的比例，但是，在模型估计过程中尚无法兼顾正负中介效应抵消的问题，所能识别出的都是中介效应非常显著的位点，而且本模型采用了平方的形式来避免结果中中介效应的相互抵消，但是采用这样的方法将导致无法直观地计算出中介效应在致病过程中所占的比例，故本研究的结果部分没有呈现中介效应大小的结果。

最后，从生物学的角度，可知基因分为主效应基因与微效基因，对于主效应基因，可能单个位点即具有显著的生物学效应，但是对于微效基因，则单个位点的生物学效应较小，只有将这些微效效应累加起来才能发挥显著的生物学效应，该模型对于微效基因甲基化位点的识别可能不显著。故以后将构建更加吻合生物学意义的中介效应模型。