三点抗折下纤维混凝土加载过程的体应变研究

张健超，翁建武，匡 川，彭少成，董必钦，洪舒贤，邢 锋

1)中国地震局工程力学研究所，地震工程与工程振动重点实验室，黑龙江哈尔滨 150080；2)深圳大学土木与交通工程学院，广东省滨海土木工程耐久性重点实验室，广东深圳518060

随着建筑工业的发展，工程结构的安全性要求越来越高．混凝土作为主要的建筑材料，对强度的要求也越来越高. 但随着混凝土强度的增加，脆性也增加．在混凝土基体中添加纤维可以减小脆性，提高材料的拉伸性能、抗裂性能和韧性[1-2]．与普通混凝土相比，随着纤维质量分数的增加，峰值强度略有增加[3]，纤维的主要作用是改善应力-应变曲线的峰后行为[4-5]．现有很多研究都是基于宏观尺寸的力学特征[6]或者利用数字图像相关(digital image correlation, DIC)分析试样表面的断裂行为[7-8]，而对材料内部在加载过程中的变化则研究较少，只停留在对表面裂缝的观察，缺乏对内部的体应变进行相应分析和断裂过程的定量研究[9]．混凝土的断裂在很大程度上削弱了结构的耐久性，影响结构使用寿命．纤维混凝土因良好的抗裂性能得到了广泛应用，有必要对其内部的断裂形貌及加载过程中的应变场演化进行深入研究．

X射线断层扫描(X-ray computed tomography, XCT)是一种无损检测试样内部微观形貌的方法，能够根据试样内部的密度和原子序数的不同，对试样进行连续扫描，然后通过对图像重构得到试样的三维形貌演化，这有助于更好地理解各种材料内部的力学性能．目前，XCT技术已被广泛用于研究混凝土的微观结构及其在变形过程中的演化[9-11]．数字体积相关(digital volume correlation, DVC)可以对XCT获得的变形前后两组数据进行分析，将子集作为匹配对象进行相关运算，计算出子集在变形前后的位移向量，并通过位移向量计算其体应变[12]．XCT与DVC相结合可以测量不同加载阶段材料内部变形后的位移和体应变．目前，它们的应用已经从骨骼扩展到复合材料的微观力学研究[13-14]．但是，该技术在纤维混凝土领域还没有足够的应用．

本研究采用XCT和DVC对三点抗折下纤维混凝土加载过程的体应变演化进行研究，通过原位加载实验跟踪其加载过程，对纤维混凝土的断裂形貌进行XCT的提取和分析，并用DVC研究不同纤维质量分数试样在不同加载阶段的体应变演化．

1 材料与实验方法

1.1 原材料

本研究制备的试样原材料包括水泥、砂、纤维和水.水泥采用普通硅酸盐水泥(P.O.42.5)．对标准砂进行筛分，得到粒径小于300 μm的砂子，堆积密度为1 610 kg/m3．纤维为聚乙烯醇纤维，纤维断裂强度为1.4 GPa, 断裂伸长率为6.0%～8.0%，杨氏模量为35 GPa，长度为(3±0.5) mm．水为去离子水．砂子、水泥和水的质量比为4∶2∶1．在砂子、水泥和水的混合物中分别添加不同质量分数的纤维(0和0.5%)．在10 mm×10 mm×10 mm的立方体模具中制备试件，然后在标准养护室中养护24 h，拆模后在相同的养护条件下养护28 d．在XCT扫描前，用砂纸磨平试样表面，使试样在加载时受力均匀．

1.2 三点抗折试验

本研究采用的XCT设备为Xradia Micro XCT-400.试样前对设备的相关参数设置如下：X射线激发电压为80 kV，功率为8 W，放大倍数为0.4倍，曝光时间为10 s．当对图像进行重构后，得到矩阵体积为1 024×1 024×1 000像素的图像．每个体素代表的实物体积为38.249 4 μm×38.249 4 μm×38.249 4 μm．在正式实验前分别对纤维质量分数为0和0.5%的试样随机抽取6个试样测定极限荷载，结果如表1．由表1可见，纤维质量分数为0和5%的试样，平均极限荷载分别为215 N和262.5 N．第1次扫描未加载状态的试样；对分别增加到50%和90%极限载荷的试样，进行第2、3次扫描；将试样加载到破坏状态，停止加载并进行第4次扫描．4次扫描时的荷载如表2．

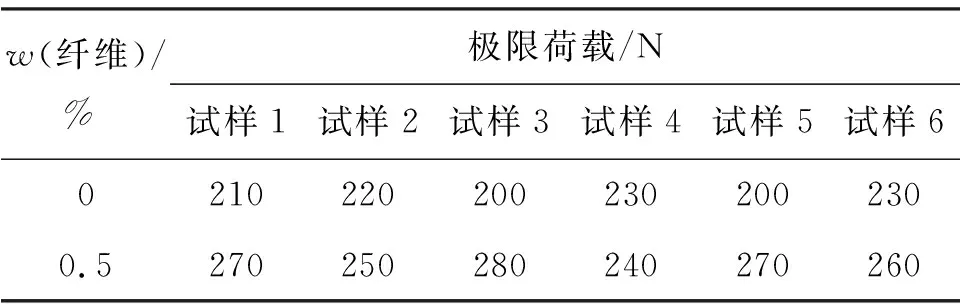
表1 不同纤维质量分数的极限荷载

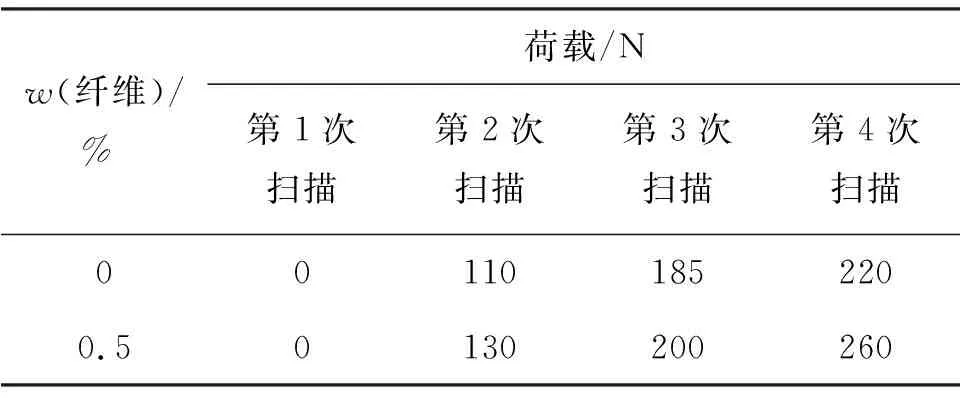
表2 四次扫描下不同纤维质量分数试样的荷载

1.3 数字体积相关技术

DVC是一种基于图像处理技术的位移和体应变分析方法．通过跟踪两幅三维图像中灰度值的变化得到位移矢量场，并计算体应变．在跟踪过程中，需要散斑材料用于图像匹配[15]．本研究采用复合材料内部的孔隙作为散斑．当对两个三维图像执行匹配计算时，需要先选取基本计算单元(子集)的尺寸和子集中心点的间距(步长)．子集尺寸影响匹配和计算结果的精度，步长则影响计算点的数量和计算时间[16]．

DVC通常将未变形的图像对象作为参考对象．其他对象被认为是变形对象．DVC进行图像匹配的相关函数是差的平方体积和(volumetric sum of squared differences, VSSD)[15]，

I(xijk,yijk,zijk)]2

(1)

其中，I(xijk,yijk,zijk)为参考图像中整数位置(xijk,yijk,zijk)处的灰度值；I′ (xijk,yijk,zijk)为变形图像中整数位置(xijk,yijk,zijk)处的灰度值，下标i、j和k分别为体图像中x、y和z方向上的体素编号．

实体对象的变形会导致图像中每个子集的平移和变形，变形图像中子体积的形状会变得更加复杂．图1显示了匹配过程中变形后子集中心点的估计位置Q． 参考图像中子集中心点P的坐标位置记为(xp,yp,zp)， 则任意点Q(x,y,z)的子集坐标为

x=xp+γ,y=yp+η,z=zp+ξ

既然是求E点的坐标，理所当然想到过点E作ES⊥x轴，垂足为S，则问题转化为求ES与AS的长，易知△ASE为等腰直角三角形，即ES=AS，所以问题转化为求FS的值．由正方形的特征想到延长SE交CD于点R，易证△ESF≌△DRE且△REC也为等腰直角三角形，则FS=ER=CR=BS=1，所以点E的坐标为(3，3)．依此类推，求M坐标自然要过点M作MK⊥x轴，垂足为K，则需求FK与MK的值．由△ESF≌△DRE想到ED=EF，即△DEF为等腰直角三角形，所以∠DFM=

(2)

其中，γ、η和ξ分别为P点到Q点位移矢量在x、y和z方向的分量．子集中单个点的位移矢量场记为f(γ,η,ξ)． 因此，变形图像中任意点的特征函数的值可表示为

I′(x,y,z)=I[xp+γ+f1(γ,η,ξ),yp+η+

f2(γ,η,ξ),zp+ξ+f3(γ,η,ξ)]

(3)

如式(3)所示，可以使用泰勒级数近似表示点P和Q的灰度值．假设子集内的位移呈线性变化，则任何点的位移矢量场可表示为

f(γ,η,ξ)=[f1,f2,f3]≈

[u(γ,η,ξ),v(γ,η,ξ),w(γ,η,ξ)]=

(4)

其中，u(γ,η,ξ)、v(γ,η,ξ)和w(γ,η,ξ)分别是变形后任意点Q的位移矢量场在x、y和z方向一阶近似下的分量．ai、bi、ci和di(i=1,2,3)是多项式系数．体应变分量εxx、εyy、εzz、εxy、εxz和εyz[17]分别为

(5)

I(xi+γ,yi+η,zi+ξ)=

(6)

其中，Hi(i=0,1,2,3)为三次Hermite多项式；Aijk是插值系数．

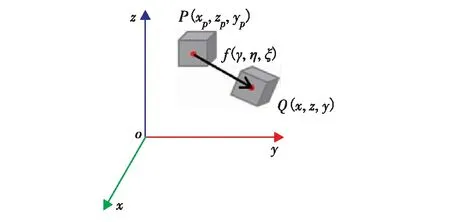
图1 子集的未变形和变形位置示意Fig.1 Schematic diagram of undeformed and deformed locations of subset

2 结果与讨论

2.1 XCT结果

在XCT扫描后将获得一系列2D投影图像，将这些图像进行重构后得到三维的体图像．图2显示了纤维质量分数为0的试样在极限载荷下的XCT重构结果，通过图2可得到试样裂缝的空间位置及走向等信息．试样中间高度处的2D切片图见图3．由图3可以明显看到裂缝、孔隙、水泥和砂子的分布情况，由于它们具有不同的X射线吸收系数，在图像上呈现出的灰度值不同．这几种材料的孔隙灰度值最具区分性，因此可以作为DVC分析的散斑材料．通过阈值分割，可以从重构图像直接提取裂缝和孔隙(图4)．提取的裂缝形貌图可以用来计算试样在三点抗折实验下最大的裂缝长度(竖向)、最大裂缝宽度和裂缝的总体积，结果如表3．从表3可见，在试样中加入纤维能有效提高抗弯强度．纤维对试样的增强作用主要体现在两个方面：一方面，纤维在试样中的三维随机分布提高了材料的抗收缩性能，进而提高了试样的强度；此外，在纤维增韧的情况下，裂纹开展需要克服纤维与基体界面处的摩擦剪应力，这也会增大试样破坏的极限荷载[17]．另一方面，纤维桥接作用引起的应力重分布使样品出现裂缝后纤维仍能提供力的传递[17]．在试样中加入纤维后，极限荷载下的裂缝长度、宽度和总体积显著减小，尤其是最大裂缝处宽度和裂缝总体积，是不掺纤维时的1/3左右．这说明在试样中加入纤维不仅能提高其抗弯强度，还能抑制裂缝的开展，降低裂缝长度和宽度．

图2 w(纤维)=0试样在极限荷载作用下的三维重构图Fig.2 3D reconstruction of the sample without fiber under ultimate load

图3 w(纤维)=0试样在极限荷载下中间高度处的切片Fig.3 Slice of the sample without fiber at middle height under ultimate load

图4 w(纤维)=0试样在极限荷载下提取的孔隙裂缝Fig.4 The pores and crack extracted from the sample without fiber under ultimate load

表3 不同纤维质量分数的XCT结果获得的极限荷载下的裂纹参数Table 3 Crack parameters obtained from XCT results with different fiber contents at ultimate load

2.2 DVC结果

通过DVC计算x、y和z方向的位移分量后，可得到试样内部各个方向的体应变分量．因为三点抗折试验中试样的体应变主要由x方向的应变分量控制，所以主要分析了不同纤维质量分数试样的x方向应变结果．图5给出了纤维质量分数为0的试样在不同加载阶段的x方向应变分量．通过对不同纤维质量分数的试件在不同加载阶段的原位检测，可以直观地观察加载过程的体应变演化．试样在50%极限载荷下，试样基本处于弹性应变状态，应变相对较小．当载荷达到极限值的90%时，应变值在部分区域逐渐增大，开始出现应变不均匀现象．当荷载达到极限值时，试样内部突然出现损伤，产生破坏裂缝，且荷载开始下降．开裂后裂缝处应变明显增大，超出极限拉应变．断裂面外区域的弹性应变流入断裂带，不过仍有部分残余应变．

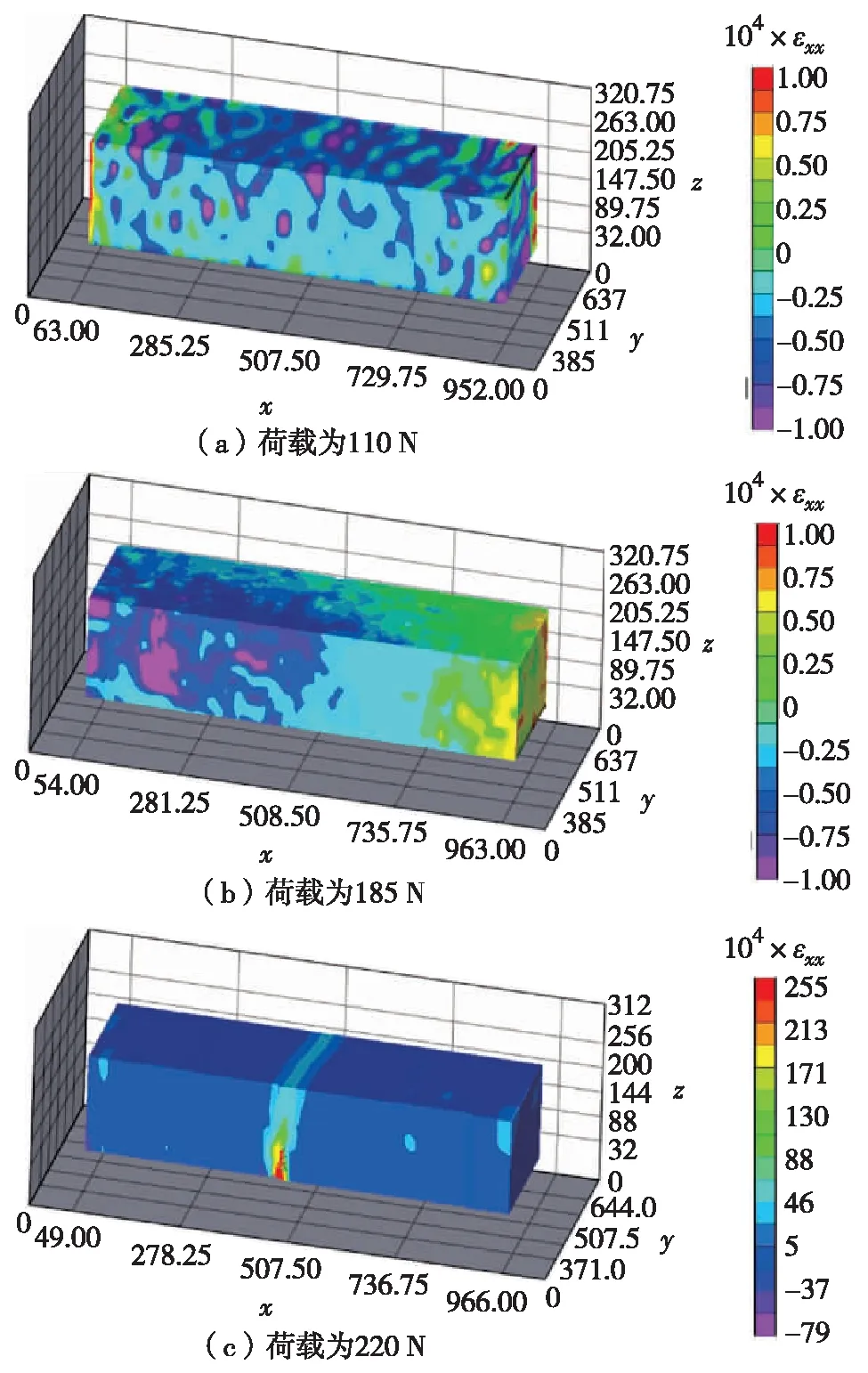
图5 w(纤维)=0试样在不同加载阶段的x方向应变分量Fig.5 εxx without fiber content at different loading stages

图6给出了纤维质量分数为0.5%的试样在不同加载阶段的x方向应变分量．可以看出体应变演化过程与纤维质量分数为0的试样呈现相同的趋势．通过对比图5和图6可以发现，破坏时，纤维质量分数为0.5%的试样具有更大的拉伸应变，最大拉伸应变是纤维质量分数为0的试样的1.5倍左右．而且，90%极限荷载时，两组试样均出现应变不均匀现象．但是纤维质量分数为0的试样应变集中程度更高，这是因为纤维的掺入减弱了试样的脆性，增大了变形能力，使试样在受载后的应变分布更加均匀．

图6 0.5%纤维质量分数试样在不同加载阶段的x方向应变分量Fig.6 εxx with 0.5% fiber content at different loading stages

另外，两组试样断裂后断裂面外均存在残留的应变，且纤维质量分数为0.5%的试样的残余应变更大些．这说明即使试样破坏时断裂面外仍然存在着变形能．这与PLANAS等[18]的研究一致，他们认为开裂过程区外试样基体的变形能会影响断裂能的确定．因此，变形能是不可忽略的(特别是在变形能力较大的试样中)，在研究断裂能时应予以考虑．

3 结 论

采用XCT和DVC进行不同纤维质量分数的纤维混凝土在三点抗折实验下不同加载阶段的体应变进行研究，可知：

1)纤维的掺入会导致试样承受的极限荷载更高．另外，开裂后裂缝的长度、宽度和体积都明显减少．

2)通过对纤维混凝土加载过程的跟踪和不同加载阶段体应变的计算，可以用XCT和DVC方法分析纤维混凝土在加载过程中的体应变演化．

3)试样破坏时断裂面外仍然存在着不可忽略的变形能(特别是在变形能力较大的试样中)，在研究断裂能时应予以考虑．