基于模糊神经网络的码头结构健康监测研究

陈 静

(交通运输部天津水运工程科学研究所 水工构造物检测、诊断与加固技术交通行业重点实验室，天津 300456)

结构健康监测技术是利用现场的无损传感与结构系统特性分析(包括结构反应)、探测结构的性态变化揭示结构损伤与结构性能劣化。也就是通过对结构的物理力学性能进行无损监测，实时监控结构的整体行为，对结构的损伤位置和程度进行诊断，对结构的服役情况、可靠性、耐久性和承载能力进行智能评估，为结构在突发事件下或结构使用状况严重异常时触发预警信号，为结构的维修、养护与管理决策提供依据和指导[1-2]。

近年来，我国港口基础设施的规模、港口吞吐能力、港口服务水平、港口结构布局得到了不断提升，但同时也存在着很多码头已经服役数十年的状况，老旧码头的加固与改造问题亟待解决。

随着数据处理和数值分析技术、实时结构监测系统和安全性的高速发展，传感器技术和物联网技术向智能化发展。结构健康监测系统已广泛应用于各个领域。区别于传统的无损检测技术是根据结构在同一位置上不同时间的测量结果的变化来识别结构的状态，码头结构健康监测技术运用直接测量确定结构的物理状态,无需历史记录数据,诊断结果很大程度上取决于测量设备的分辨率和精度[3]。

码头结构的监测参数主要包括应力应变、整体沉降、相对位移等，监测数据的获取仍然依赖于各种传感器。然而，由于码头长度的差异、传感器的安装和维护成本昂贵以及传感器信号不稳定等因素导致所获取的数据不准确，导致难以有效地对码头结构的健康状况进行准确判定[4-5]。

为提高结构监测数据的准确性，本文提出了一种基于模糊神经网络的数据融合技术，即通过无线传感器网络，利用模糊神经网络的无线映射能力、较强的环境自适应学习能力和稳定性，搭建模糊神经网络模型实现数据融合。

1 无线传感器网络扩展结构

无线传感器网络技术不断向低功耗和低成本发展，在码头结构监测的无线传感器网络中具有明显的优势。

无线传感器网络由三部分组成，分别是传感器层、数据收集和传输层以及数据应用层，如图1所示[6]。在传感器层、各种传感器分布在码头结构的关键点(即监控点)。第二层是从传感器收集数据并进行远程传输到数据中心。通常数据中心是服务器或云存储。数据应用层对数据进行显示和进一步分析。在研究中模糊神经网络被嵌入到无线传感器网络中。

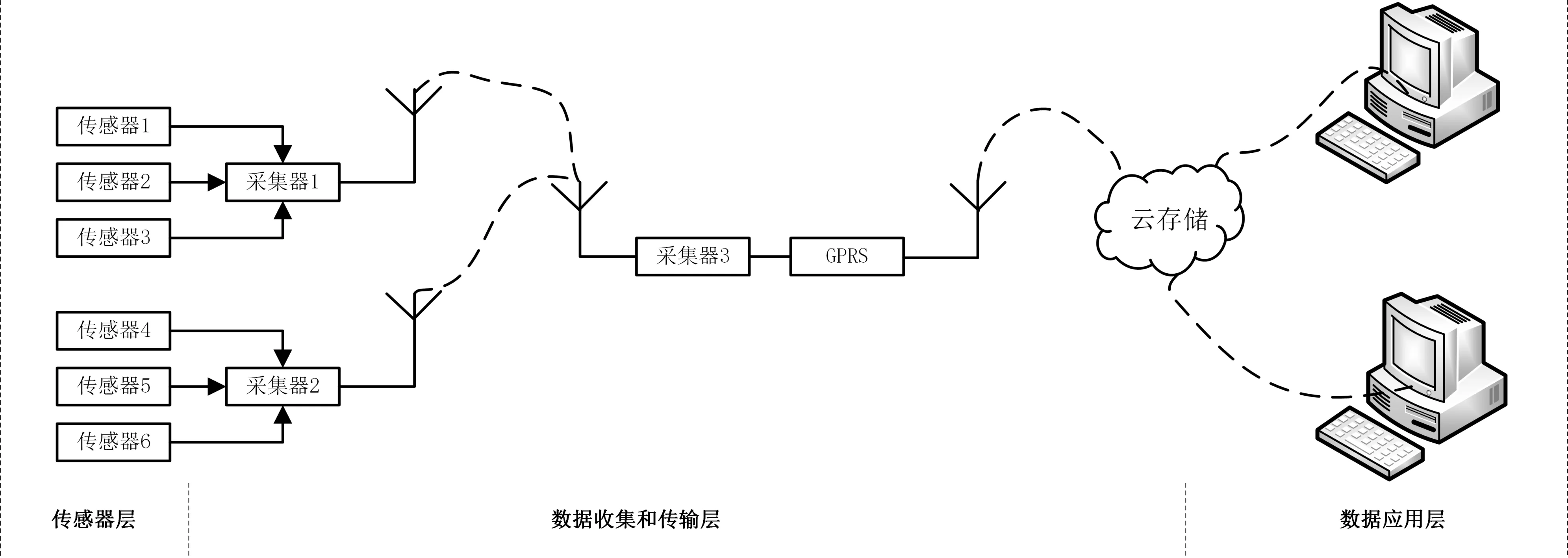
图1 网络体系结构Fig.1 Network architecture

2 模糊神经网络

2.1 数据预处理和特征参数提取

模糊神经网络具有无线映射能力、较强的环境自适应学习能力和鲁棒性。因此健康监测有可能将目前广泛采用的离线、静态、被动的损伤检测，转变为在线、动态、实时的监测与控制，这将导致工程结构安全监控、减灾防灾领域的一场革命[7-8]。然而，仅使用模糊神经网络来检测结构的损坏具有易于误诊和漏诊的缺点。

为了充分利用从监控系统中收集到的大量数据，本文提出了一种基于数据融合技术的数据处理方法，该方法可以利用冗余和补充信息来评估结构的健康状况，如图2所示。

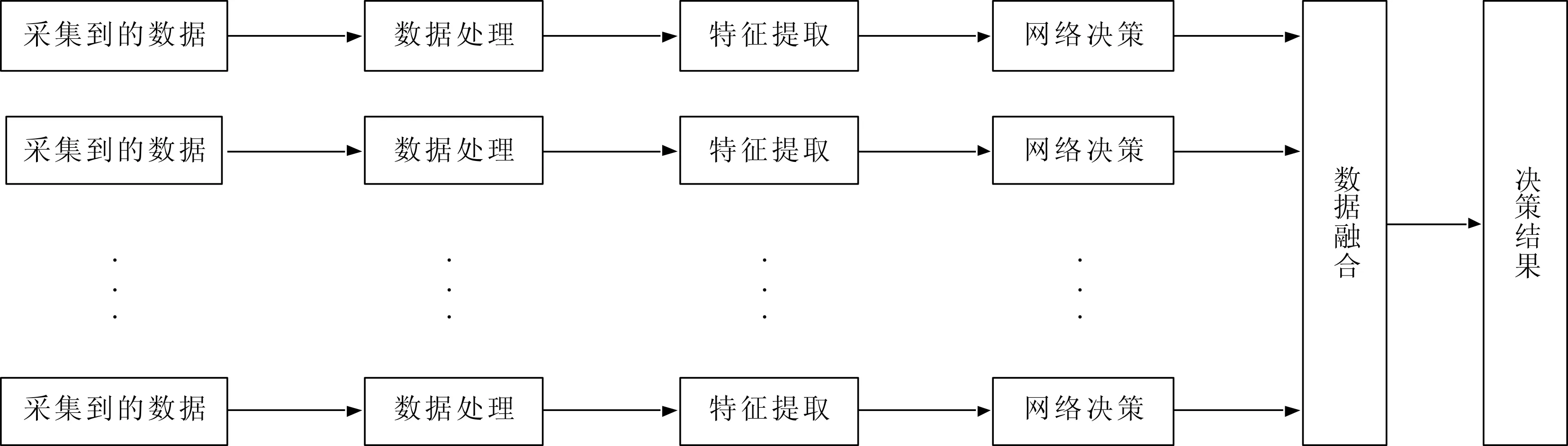
图2 损伤检测Fig.2 Damage detection

结构监测系统的响应参数可以分为三种，分别是频率信号、模拟信号和数字信号[9]。同时，在环境和监测仪器的影响下，实际测量参数中包含噪声和误差，在数据预处理中，首先将数据转换为数字信号形式，然后使用平均值法和阈值法等处理原始信息去除噪音。

结构振动参数是重要的监测指标。振动传感器输出的信号为模拟信号，转换为数字信号后，特征提取过程采用傅立叶变换使数据在频域中表示[10]。经典傅立叶转换公式可将模拟信号转换为数字信号，如式(1)所示。

(1)

在实际应用中，需使用离散傅立叶级数对信号进行分析，如式(2)所示。

(2)

在数据预处理和特征提取后，数据信息全部变为数字信号，并通过傅立叶变换将振动信号以频域的形式表达。这种数据预处理将对后续的处理带来便利。

2.2 模糊神经网络模型

模糊神经网络通常由模糊化功能、神经网络结构和去模糊化功能组成[11]，如图3所示。

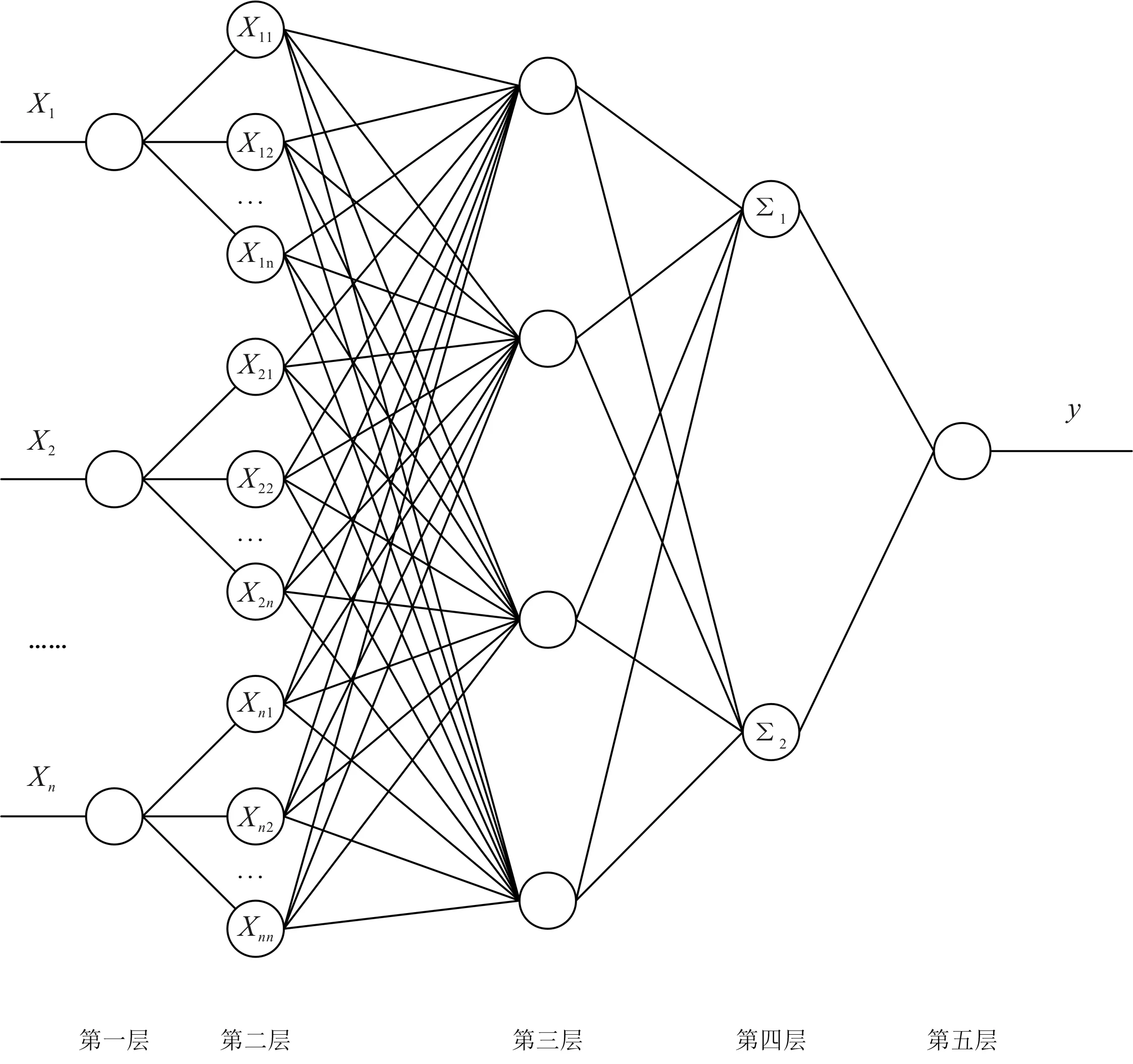
图3 模糊神经网络结构Fig.3 Fuzzy neural network structure

在图3中，模糊神经网络是五层结构，第一层是传感器输入层。其中每个神经元对应于代表传感器输入数据的输入变量，每个神经元将数据直接传递到第二层神经元，层的权重为1。

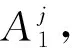
y=Bj∈(j=1，2，…，R；i=1，2，…，n)

(3)

式(3)中的Bj是一种隶属函数，它可以转变为式(4)

y=yj(j=1,2,…,R)

(4)

假设j为y的隶属函数，则模糊系统可以用式(5)表示

(5)

其中μj可以表示为式(6)

(6)

第三层是隐藏层。该层的功能是实现输入变量的模糊化值与输出变量的模糊化值之间的映射。输出的适应度值如式(6)所示。

神经网络的第四层是输出层。输出的值是式(5)的分子和分母。该值对应于结构的损坏模式，同时第四层和第五层共同完成去模糊功能。

模糊神经网络的实现需要两个步骤。首先，初始化每个节点的值，主要是设置参数。其次，通过系统学习输入和输出样本，建立逼近模糊非线性函数的映射关系。

2.3 神经网络学习算法

BP神经网络算法是一种制导算法，它包括正向和反向计算步骤。假设学习样本的数量n，输入向量是x=(x1,x2,…,xn)T，期望的输出是Y=(Y1，Y2，…，Yn)T，Opi是单位i的输出，Wij是网络的权重值，δ是误差信号，θi是阈值，学习步骤如下所示。

第一步是初始化网络权重值Wij(0)和阈值θi，它们将被定义为区间[-1,1]内的随机数。

第二步是输入学习样本集{Xk，Yk}，k=1,2,…,n。

第三步，传递函数是S形函数，表达式如式(7)所示。

(7)

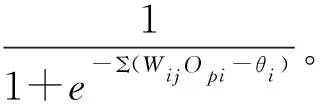
因此可以获得网络的输出误差

(8)

(9)

假设平均系统误差容限为Es，单个样本误差容限为Eps。第四步是如果E≤Es或Ep≤Eps或达到指定的迭代步骤数，则学习过程将结束。否则，误差将继续向后传播，然后转到第五步。

第五步是反向计算每个网络单元的误差。其中输出层误差如式(10)所示，隐藏层误差如式(11)所示

δpj=Opj(1-Opj)(Tpj-Opj)

(10)

δpj=Opj(1-Opj)Σδpl-Wpl

(11)

第六步是计算权重和阈值的正确参数，如式(12)和式(13)所示

△Wij(n+1)=ηδpjOpj+∂△Wij(n)

(12)

△θj(n+1)=ηδpj+∂△θj(n)

(13)

第七步是校正权重和阈值，如式(14)和式(15)所示

Wij(n+1)=Wij(n)+△Wij(n+1)

(14)

θj(n+1)=θj(n)+△θj(n+1)

(15)

整个神经网络的流程如图4所示。

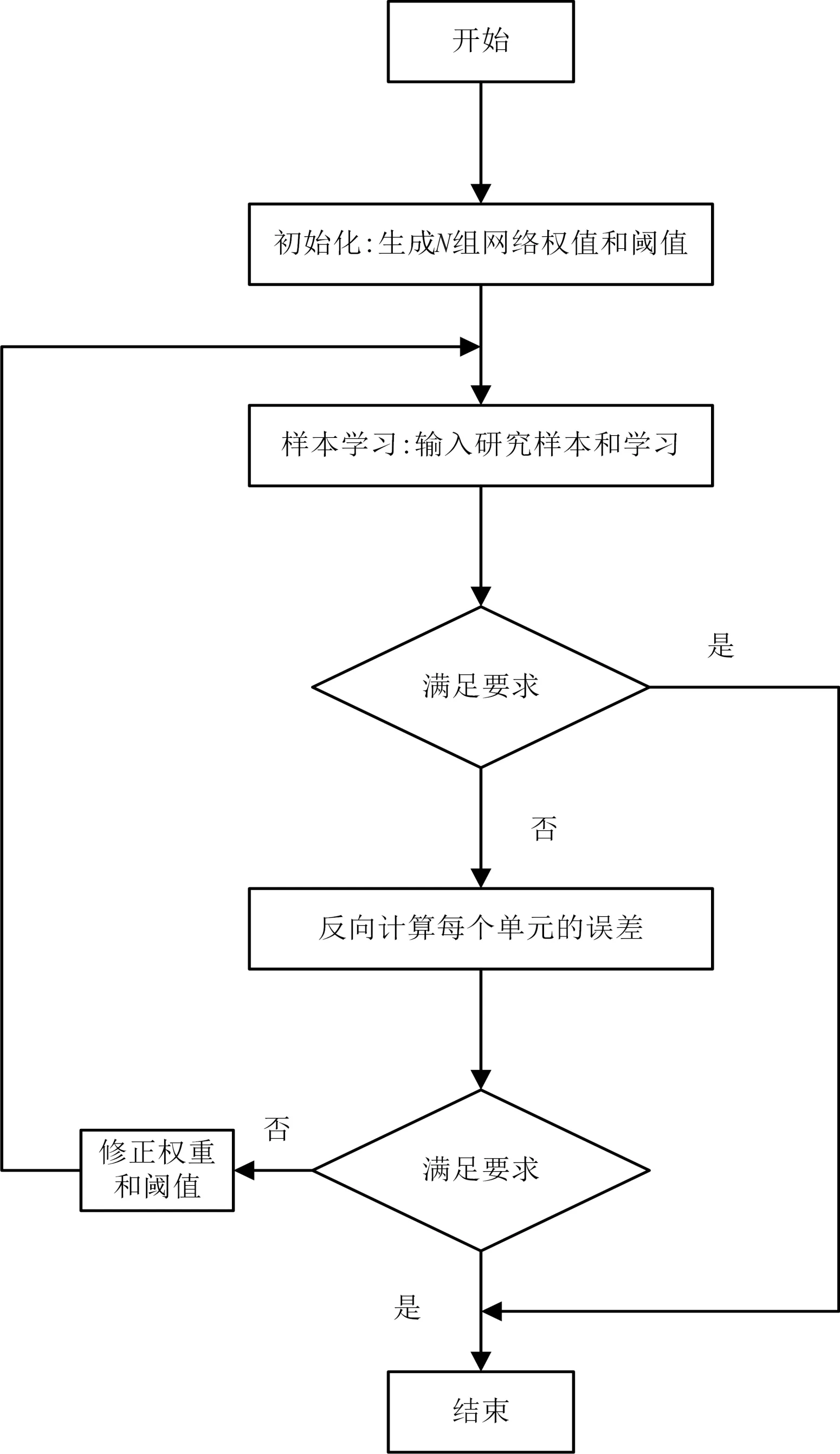
图4 神经网络流程图Fig.4 Flow chart of neural network

2.4 模糊神经网络训练样本

为了使监控系统有效运行，建立准确的训练样本非常关键。通过研究样本，系统将在输入和输出数据之间建立一个映射关系。通过精确的有限元方法可以获得样品。本文选择天津某高桩码头前承台典型结构，重点针对码头应力应变和桩体位移两项数据进行讨论。选择有限元分析软件并将接触元件类型设置为target170和contac173。使用经典的Peter Drucker-prager模型选择地面。

本文计算了模拟载荷并获得了载荷-应变关系，部分结果如表1所示。

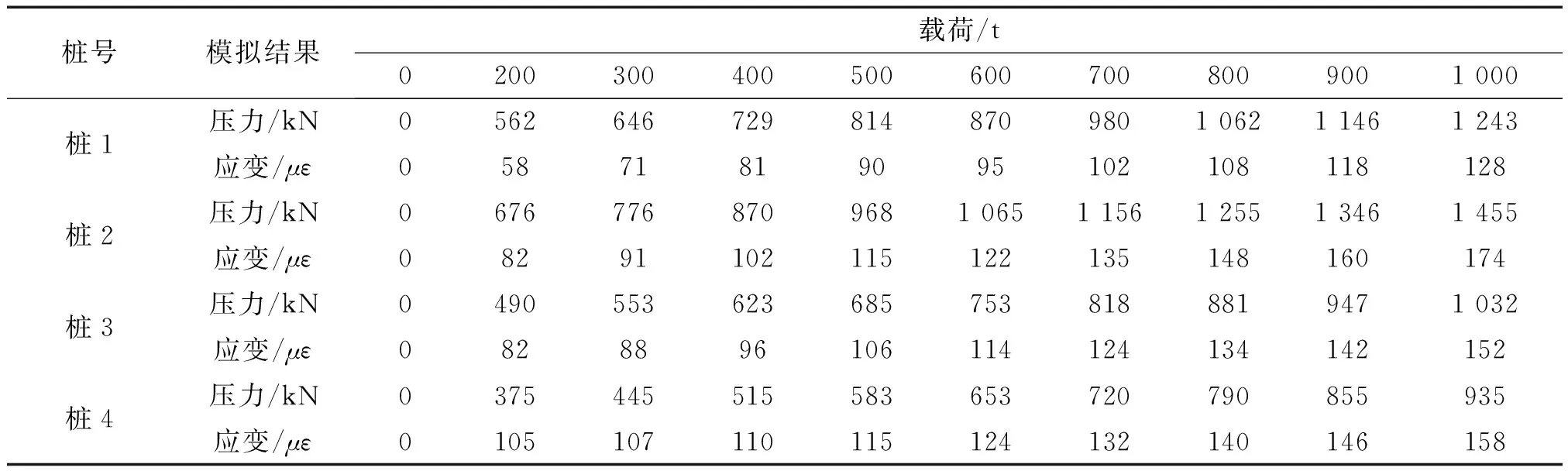
表1 软件模拟应变结果Tab.1 Software strain simulation results

在负载测试阶段，本文采用了单点位移计测量方法。监测点的载荷-应变关系如表2所示。为了保证一致性，在有限元分析时监测点与观测点是一致的。

表2 应变计测量结果Tab.2 Results of strain displacement meter measurement με

码头的桩仅看作承受轴向压力，根据有关材料力学公式可知，压力和应变是线性关系的，见式(16)

σ=Egε，F=σgA

(16)

式中：σ为应力，MPa；ε为应变，με；F为压力，kN；E为构件材料弹性模量，MPa；A为构件断面积。该码头混凝土桩构件的材料弹性模量E=3.35×104MPa，A=0.3 m2。

本文将模糊神经网络引入到结构监测系统中，最终的数据从智能算法得到，结果如表3所示。

表3 模糊神经网络计算结果Tab.3 Calculation results of fuzzy neural network με

为了验证计算数据的可行性，位移计测量数据与模糊神经网络产生的数据如图5所示，将实际数据与模糊神经网络产生数据、有限元计算数据相比较，可知模糊神经网络产生数据更倾向于计算数据。另外，模糊神经网络可以更好地消除系统的噪声和误差。

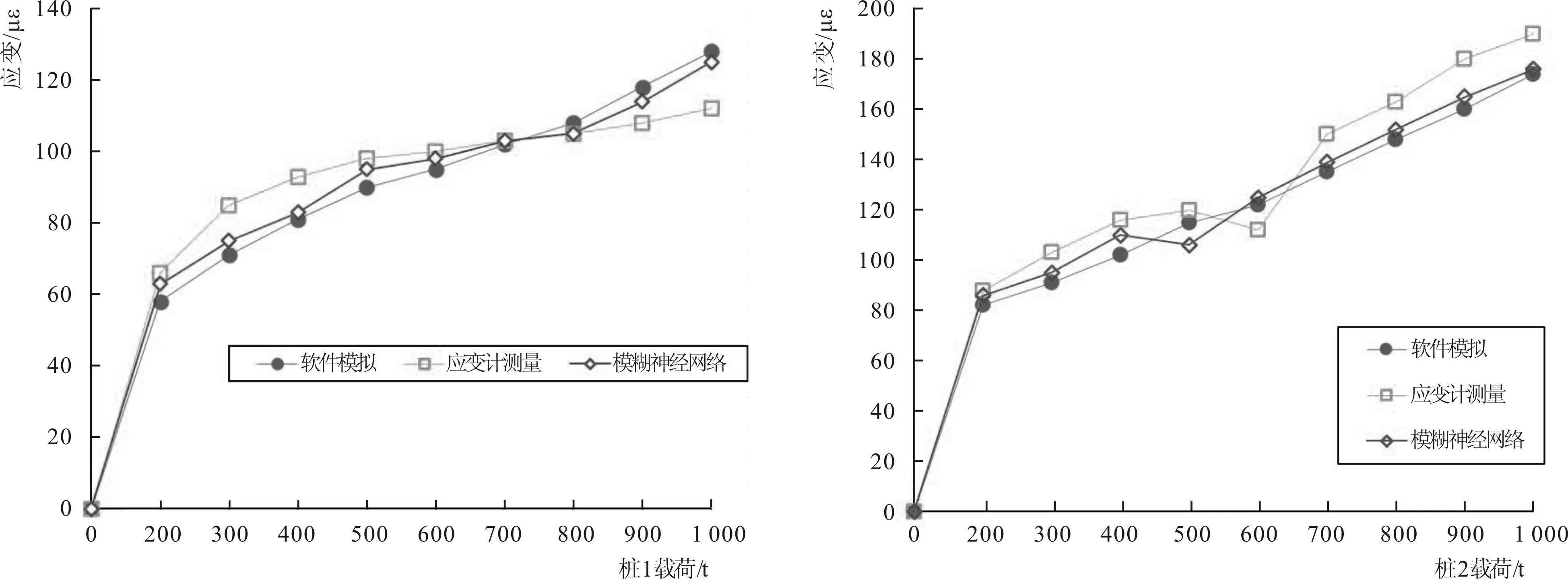
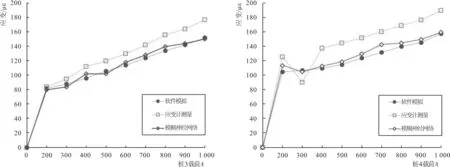
图5 不同方法下的数据处理结果Fig.5 Data processing results of different methods

3 结论

为解决结构监测系统数据的准确性问题，本文采用无线传感器网络，利用模糊神经网络实现数据融合。提出了一种基于数据融合技术的五阶段数据处理方法，由于模糊神经网络具有神经网络的无线映射能力、较强的环境自适应学习能力和鲁棒性，可以利用冗余和互补数据消除来自环境的噪声和误差。通过有限元分析方法获得神经网络的训练样本，并将该系统应用于无线传感器网络，结果表明模糊神经网络在码头结构监测系统中具有优势和可行性，在实际应用中可以获得更准确的数据。