Morison公式在悬浮隧道波浪荷载计算中的运用研究

杨艺平, 朱 峰, 陈良志, 钱原铭

(中交第四航务工程勘察设计院有限公司，广州 510230)

水下悬浮隧道是一种建设悬浮在水中的大型跨海交通工程，主要解决的是人类未来实现深水、宽水域的跨越问题。因其巨大的跨越能力、优良的环境适应性和低建造成本等优点，今后有望成为海洋开发的关键技术[1-2]。作为一种全新的工程结构，悬浮隧道工程在规划、设计、施工、维护管理等各阶段仍有众多待研究的技术课题。尤其在复杂的海洋环境中，波浪对悬浮隧道产生的荷载是结构强度分析中的重点之一，因此研究悬浮隧道工程中波浪荷载的计算方法具有非常重要的意义[3-4]。

对于常规的悬浮隧道工程，由于交通车道数的需要，所拟定的悬浮隧道结构物的等效直径D一般为10～25 m，设计波浪的周期T一般在10 s左右，波长L约为160 m，故D/L为0.06～0.16。在海岸工程结构流体载荷的计算中，一般认为当结构物的等效直径D与波浪波长L之比小于0.2时，可以忽略波浪绕射的影响，采用只考虑水的黏性和惯性作用的Morison方程[5-8]。因此，许多学者都对此展开了研究。其中，Kunisu[9]对Morison公式法和绕射理论进行了详细的对比，并讨论了Morison公式的适用性；麦继婷等[5]利用 Morison方程和线性波浪理论，计算分析了隧道放置深度、海流速度、流向与波向间的夹角、波浪周期等诸多因素对水平波浪荷载的影响；项贻强和张科乾[6]结合Morison方程，提出了沿悬浮隧道表面进行分层积分的方法来计算悬浮隧道水平波浪荷载和竖向波浪荷载。但以上的研究均假定公式计算所涉及的各参数为已知且精确的，而实际工程运用中，各个参数的获取往往是困难或者需要投入巨大人力物力；同时，以上研究默认结构物各点同时受到了最大波峰力作用，而实际工程中悬浮隧道跨度极大，结构各点所受的波浪荷载存在相位差。因此有必要研究各计算因素对计算结果的影响，进而指导工程运用，对不同敏感度的影响因素给予不同程度的关注度。

基于此，本文以松恩海峡方案设计中的悬浮隧道工程为例，通过公式计算和流体数值模拟的结果对比，验证了Morison公式在本工程的适用性；并对公式中某些因素，包括公式中流体系数(CD和Cm)取值、海洋生物生长厚度、是否考虑结构不同位置的波浪相位差等，进行敏感性分析。

1 悬浮隧道波浪荷载计算方法简介

1.1 结构计算模型简化

对如图1所示受流体波浪力作用的悬浮隧道结构，假设[5]：

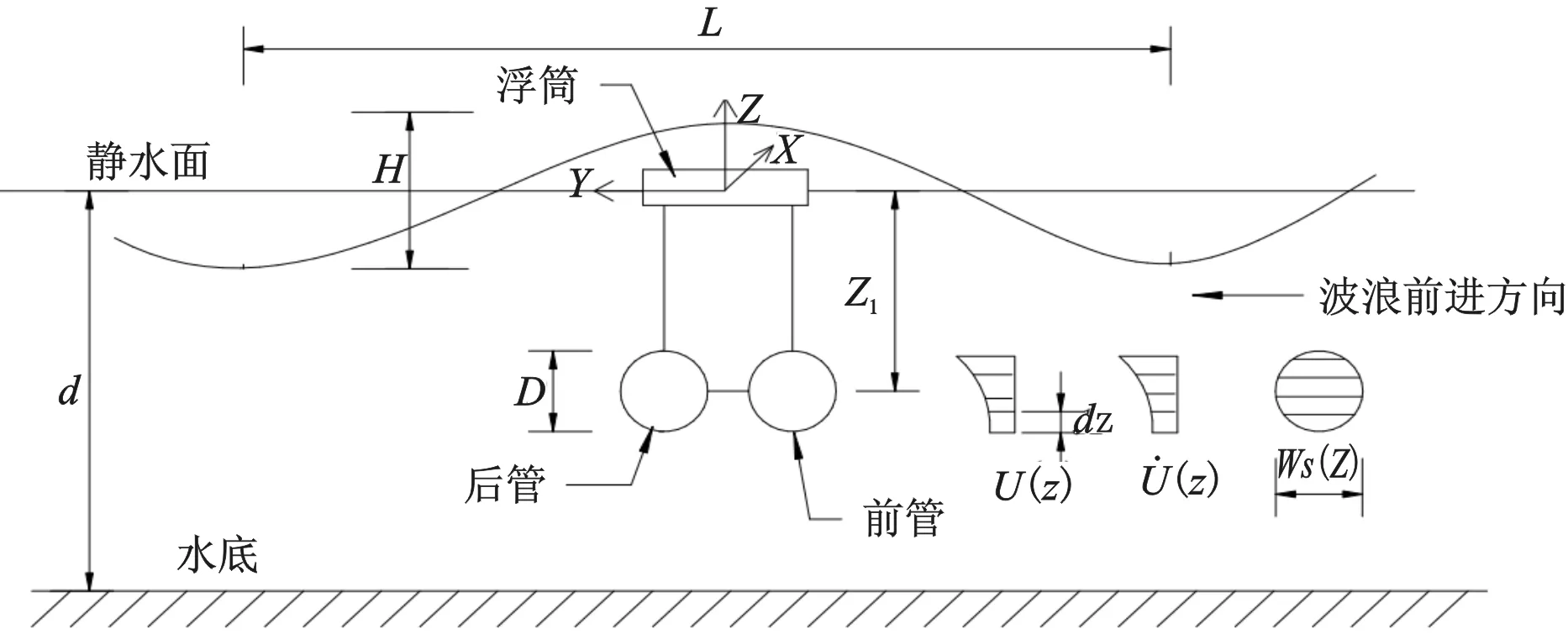
图1 简化模型图示Fig.1 Sketch of calculated model

(1)悬浮隧道淹没在水下一定深度处，由桩基、锚索或者浮筒固定，忽略结构在荷载作用下的变形和位移，假定结构是绝对静止不动的刚体。

(2)为了推求方便，坐标系建立如图1所示：z轴竖直向上，x轴与悬浮隧道轴线平行，y轴为波动方向，坐标原点位于静水面处。

(3)流体是理想的、不可压缩的，运动是无旋的。

(4)考虑到结构断面尺寸较大，波浪在各高程处作用力不同，采用沿结构表面分层积分的方式计算波浪荷载[5]。

图1中，d为设计水深；L为设计波长；D为悬浮隧道的等效直径；H为设计波高；Z1为静水面与隧道沉管中心的距离。

1.2 Morison公式理论简介

Morison公式是Morison、O′Brien和Johnson在1950年前后提出的一个半经验半理论公式，该公式假定总波浪荷载由波浪速度力和惯性分力两部分组成，其表达如式(1)～(3)所示[10-12]

FW=FD+FI

(1)

(2)

(3)

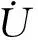
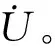
2 工程实例计算

2.1 工程概况

本次研究以方案设计阶段的挪威松恩海峡浮筒悬浮隧道工程为案例，拟建的隧道在江面上的跨度约3 700 m，中轴线为一个半径2 682 m、弦长740 m的弧线。该悬浮隧道主要由两个直径D为12.6 m的沉管、主沉管间的连管、漂浮在水面的浮筒，以及浮筒与沉管连接的拉管等部分组成。两个沉管的间距为40 m,其轴线到静水面距离Z1约为26.80 m，为双向4车道。其结构平面图和典型的剖面图如图2、图3所示。

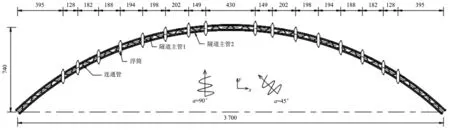
图2 结构平面图(单位：m)Fig.2 General layout of the submerged floating tunnel scheme

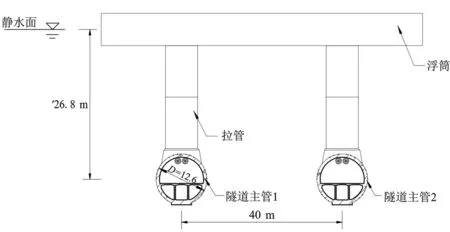
图3 结构典型剖面图(单位：m)Fig.3 Typical section of structure

2.2 波浪条件

设计最大波高Hmax=4.54 m，设计波周期为T=7.0 s，设计水深取h=100.00 m，隧道长度考虑单位长度l=1.00 m；静水面标高为1.20 m；海水密度为1 025 kg/m3。

2.3 Morison公式计算法

首先采用Morison公式计算作用在悬浮隧道主沉管上的波浪荷载，其速度力系数CD和惯性力系数Cm按圆形截面的构件，依据英国规范《Maritime Structures-Part1: Code of Practice for General Criteria》(BS6349-1:2 000)进行取值：取CD=1.2，Cm=2.0[13]。并假定隧道表面光滑，无海洋生物附着，忽略海流速度的影响;不考前后两管间波浪反射对波浪作用的影响，只计算前管受到的波浪荷载。由此计算得到的波浪荷载，包括水平向和竖直向波浪荷载，随时间变化的历程曲线如图4所示。

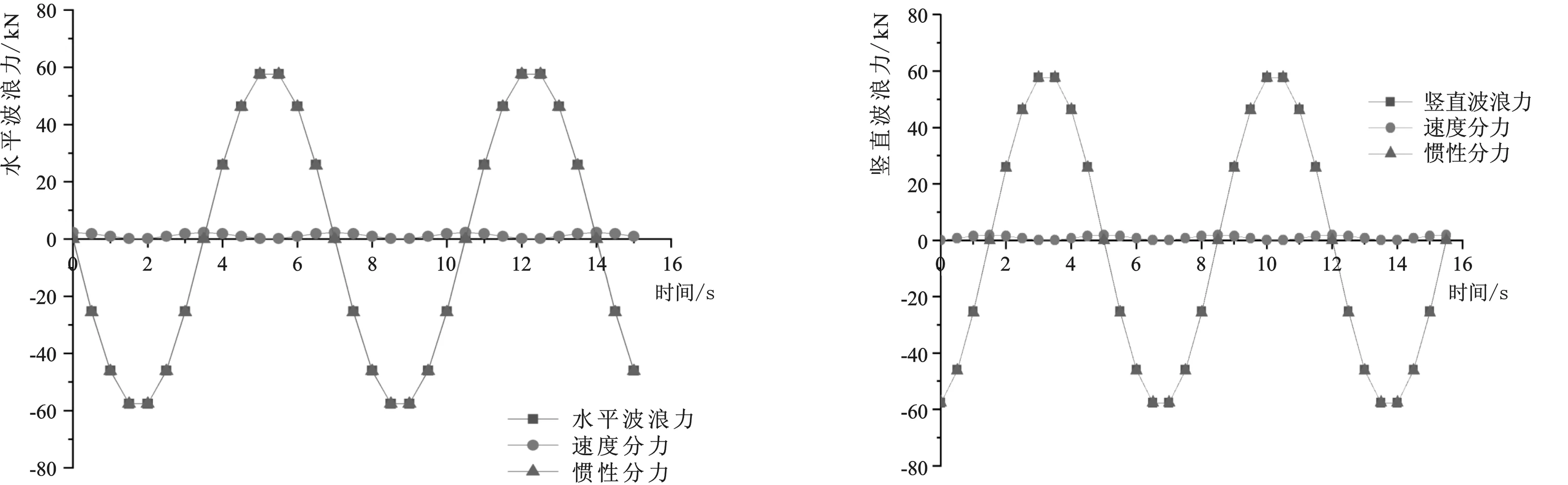
4-a 水平分力4-b 竖向分力图4 波浪荷载时间历程曲线Fig.4 Time course curves of wave load

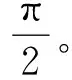
2.4 CFD 数值模拟

为了验证上述解析解的正确性，基于有限体积法的流固耦合理论建立了悬浮隧道二维水流数学模型，计算模拟了波浪荷载对悬浮隧道的作用过程。

2.4.1 数值模拟计算理论

有限体积法开展流体动力学计算需要基于三大控制方程：质量守恒方程、动量守恒方程和能量守恒方程，其中能量守恒方程不是必须的[3,14]。

(1)质量守恒方程。

根据控制体中水体质量保持不变的原则，质量守恒方程如式(4)所示

(4)

式中：VF是流动介质的体积分数；ρ是流体介质密度；RSOR为质量源；ξ是坐标系数(直角坐标取0，柱坐标取1)；Ax,Ay,Az为三个方向流体运动的面积分数；u,v,w对应三个方向的速度分量。

(2)动量守恒方程。

根据控制体中水体运动的动量与外力冲量的平衡关系，动量守恒方程如式(5)所示

(5)

式中：Gx，Gy，Gz为流体在三个方向所受体力；fx，fy，fz为流体在三个方向所受面力；bx,by,bz为多孔介质中的水头损失。

(3)RNG紊流模型。

RNG模型在低速流动(<10 m/s)环境下与紊流粘性耗散的实验结果吻合度较高，对波浪运动的各种形态模拟精度较高且计算时间增加较少，因此广泛应用于水流与波浪模拟中。

紊流模型区别于层流模型的一个特点就是在控制方程中添加了紊流动能输运项，紊流动能输运方程如式(6)所示

(6)

式中：PT表示由于速度梯度而产生的紊流动能源；GT表示由于浮力而产生的紊流动能源(不可压缩流体该项为0)；εT表示紊流动能耗散项。

2.4.2 数值模拟计算模型

(1)为了获得相对均匀的来流条件，保证进出口边界远离隧道影响的流体范围，本文设置数值模型在水流方向的长度为1 000 m。

(2)在流体数值模拟中，计算网格尺寸是控制计算结果的一个关键问题，尤其是在以流体剪切拖曳力占主导作用的条件下。本文经过各类综合试算对比，在计算成本和计算精度之间取平衡，采用的网格尺寸为500 mm。

(3)为了获得稳定的波浪，计算时间取为1 000 s。

(4)各波浪参数取值与2.2节相同，按规则波工况进行考虑。

2.4.3 计算结果

采用软件对上述模型进行建模计算，典型的波浪作用过程如图5所示，计算得隧道前管的流体作用力计算结果如图6所示。

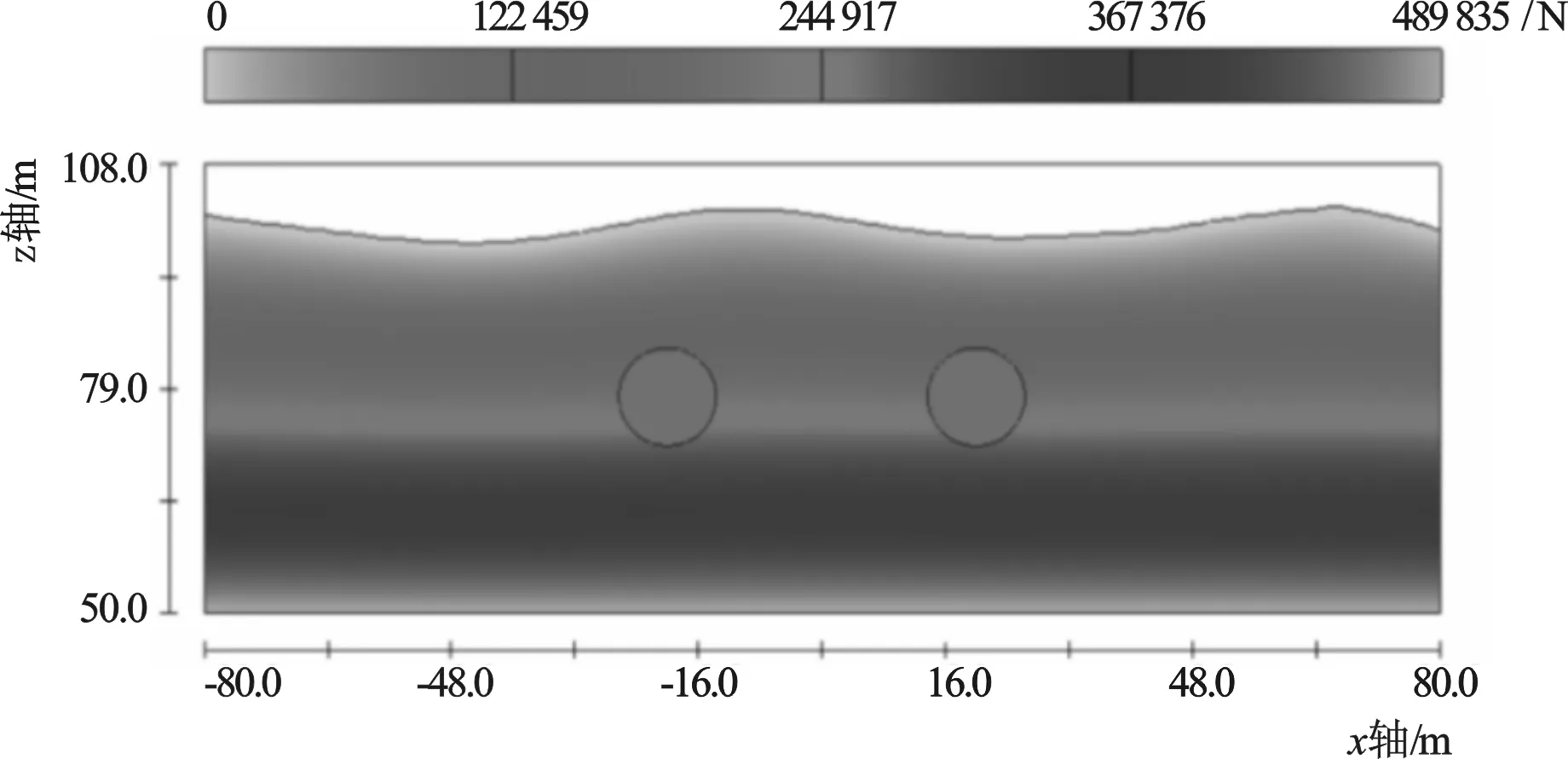
图5 隧道管体所受到波浪荷载云图Fig.5 Typical process of wave force acting on tunnel pipe

从图6中可以看到：在波浪稳定传播期，前管的水平力为60 kN，竖向流体力极差±40 kN。考虑本计算模型中竖向流体力包含浮力和波浪荷载，浮力值恒定，因此竖向流体力的极差即为波浪竖向力。

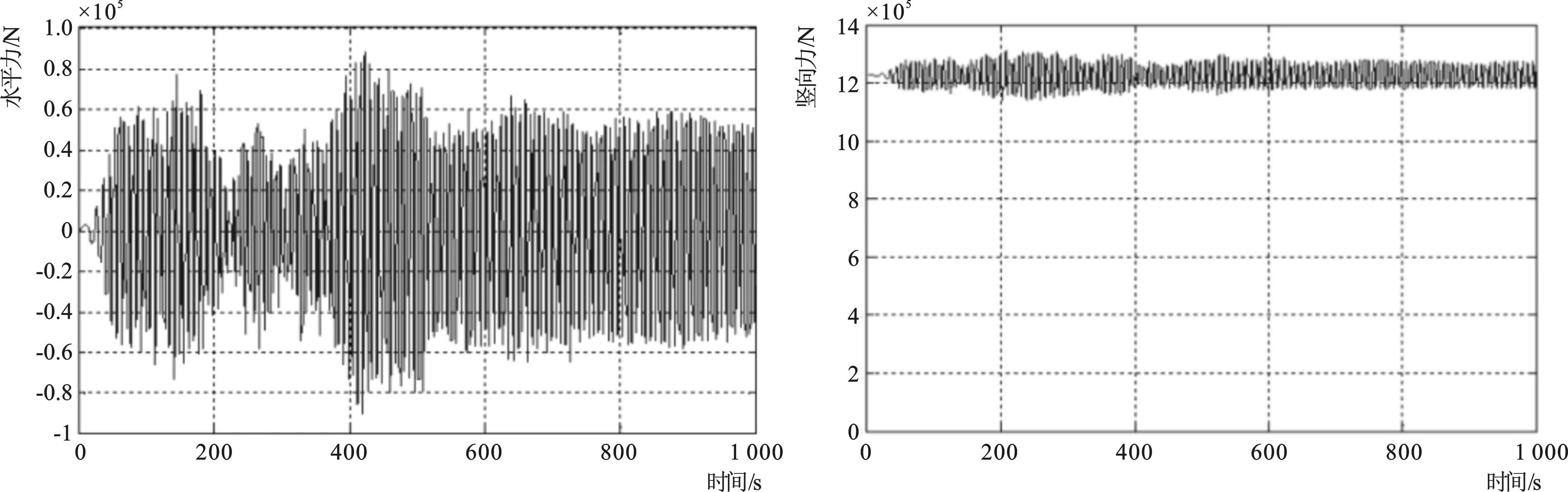
6-a 水平向6-b 竖直向图6 规则波作用下波浪荷载时间历程曲线Fig.6 Time series of wave load under regular wave action

2.5 Morison公式和数值模拟的结果对比

由以上的计算结果可以看出：

(1)Morison公式与数值模拟的计算结果较为吻合。尤其是最大水平波浪荷载，由Morison 公式计算结果为57.6 kN/m,与数值模拟的60 kN/m，两者相差小于4%。采用Morison公式计算作用在悬浮隧道的波浪荷载，在工程设计中是可行的。相比数值模拟，采用公式进行计算更加简单、方便。

(2)采用Morison公式计算得到的波浪荷载中，波浪荷载的惯性分力远大于其速度力分力，本例中速度力约为惯性力的1%。这是由于一般悬浮隧道的结构尺寸较大，单位长度对应的体积在数值上远大于其面积。

(3)由于悬浮隧道工程相当于一根水平放置的细长结构物，用Morison公式和线性波理论计算得到的水平波浪荷载和竖向波浪荷载大小相等，历时曲线形态一致；并且总波浪荷载由惯性分力主导，其历时曲线基本成正弦分布。

3 计算影响因素敏感性分析

由于海况的复杂性和实验条件的限制等，在实际的工程中为了得到准确的参数往往花费巨大的人力物力，甚至大部分情况下难于得到精确的值。因此有必要根据悬浮隧道工程的特点，分析各计算要素对计算结果的影响程度，根据其对计算结果的重要性给以不同程度的关注度。

3.1 水流系数的敏感性分析

采用Morison 公式计算波浪荷载只是一种工程上的近似，计算结果是否反应实际情况，需要通过公式中速度力系数CD和惯性力系数Cm进行调整。关于该系数的取值，一般认为对于圆柱体构件，速度力系数CD为0.7～1.2，惯性力系数Cm为1.6～2.0[15]。据此，在其它参数取值不变的情况下依次调整不同的CD和Cm值，得到其对波浪荷载(峰值)计算结果的影响如图7所示。

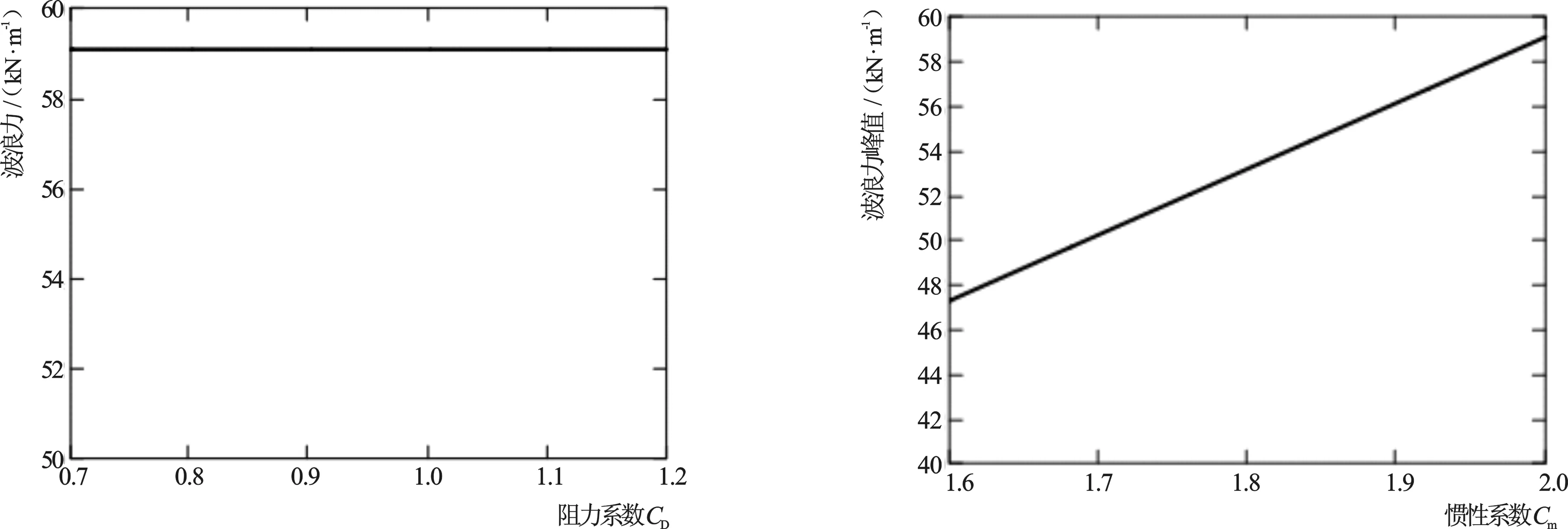
图7 CD 、Cm系数对波浪荷载峰值的影响Fig.7 Influence of CD and Cm coefficient on wave load peak value

由图7可以看出，速度力系数CD对波浪荷载几乎没有影响，而惯性力系数Cm与计算结果基本成线性关系。这是因为在悬浮隧道工程中，波浪荷载中惯性力起主导作用，因此与惯性力直接相关的惯性力系数Cm对计算结果的影响成线性，而速度力系数几乎不构成影响。在实际工程运用中，应对惯性力系数Cm的取值进行重点关注。

3.2 海洋生物生长厚度的敏感性分析

附着在结构表面的海洋生物一方面会增加截面的有效面积，其变化值可以通过简单的几何计算得出；另一方面会影响结构的粗糙度，进而影响水流系数，这难于定量分析。其中，由3.1节的分析可知，在悬浮隧道工程中，速度力系数CD对计算结果影响不大，因此本节计算中忽略CD值的变化。而根据相关的研究，惯性力系数Cm与相对粗糙度k/D(k是结构物上硬海洋生物组织最点到最低点的平均厚度)的关系如图8 所示[13，15]。

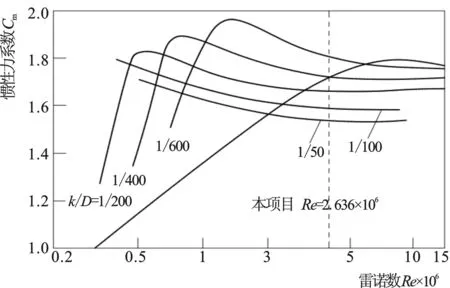
图8 粗糙度与Cm的关系曲线Fig.8 Relationship curve between the roughness and Cm coefficient

表1 本项目中不同粗糙度对应的Cm值Tab.1 The Cm values for different roughness in this project

由图8可知，相对粗糙度与Cm值的关系性较差，在一定水体雷诺数范围内，两者成负相关，随着水体雷诺数的继续增加，相对粗糙度对Cm的影响逐渐减弱。具体在本工程的条件下(雷诺数Re=2.636×106)，其Cm值在1.49～1.91区间变化，如表1所示。

因此在第3节的条件基础上，假定附着隧道表面海洋生物的厚度由0 m增加到0.25 m(相对粗糙度k=1/600～1/50)。同时考虑几何尺寸和流体系数的变化，其计算得到的波浪峰值如图9所示。

由计算结果可得，波浪荷载随海洋生物厚度的增长而变小，变化幅度约为13%，变化曲线基本与相对粗糙度和Cm的关系曲线一致。说明海洋生物对计算结果的影响主要是由惯性力系数Cm变化引起的。这是因为悬浮隧道的有效管径一般较大，相比之下海洋生物厚度较小，其附加厚度导致截面面积或者体积的增加量可以忽略不计。鉴于此，在实际工程中获取惯性力系数Cm值时应该充分考虑海洋生物的影响。

3.3 波峰线及波向角度对结构的影响

在以上的计算中，只考虑单位长度的结构受荷，均忽略了隧道沉管不同位置的波浪相位差。而实际的工程中，由于悬浮隧道的跨度极大，在同一时刻结构中沿线各点与波峰距离各不相同，所受的波浪荷载存在相位差。

为了研究这种影响，本节进一步考虑在同一时刻隧道沿线不同位置的相位差。并假定波峰线为直线，分别考虑波浪入射角为a=90°和a=45°两种工况，如图2所示。计算得若干个典型时刻的波浪水平力沿着隧道轴线方向(X轴)的分布如图10所示。

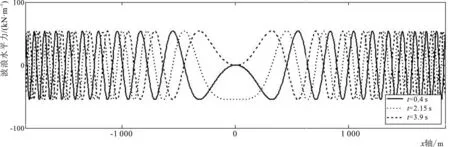
10-a a=90°

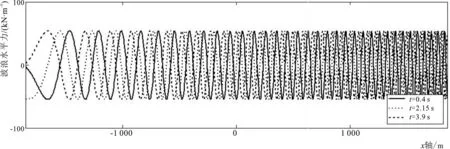
10-b a=45°图10 波浪水平力随着隧道x轴方向的分布Fig.10 Distribution of wave horizontal force along x-axis direction of tunnel

相应结构的内力最大值如表2所示。

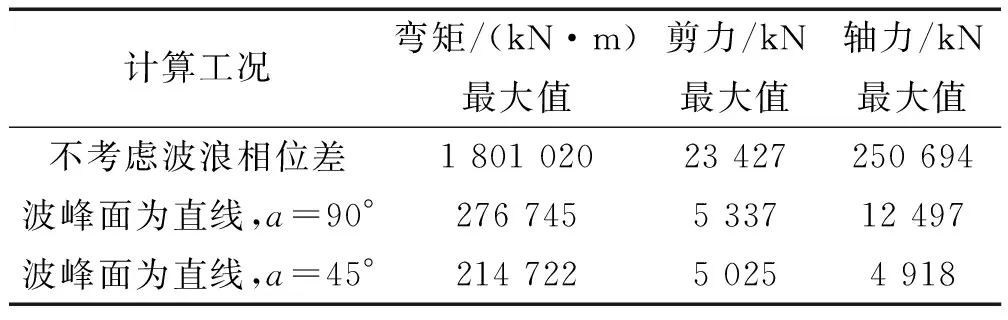
表2 不同波浪工况下结构内力计算结果Tab.2 Structural internal force in different wave conditions

由图10和表2可得，由于悬浮隧道跨度极大，同一时刻结构各点的波浪存在较大相位差，波浪荷载随结构位置的变化而不断变化，进一步影响了结构内力分布。在松恩海峡悬浮隧道工程中，这种影响甚至达到一个量级。因此，将最大的波浪荷载峰值直接施加在结构各点中的常规算法过于保守，计算结果偏大。

本次研究假设波峰线为直线，而现实工程中海况更加复杂、多变、随机，波峰线的形态更加多样。因此实际项目过程中，应充分调查波群的分布规律，考虑结构不同位置的波浪相位差，使结果更为准确。

4 结语

(1)悬浮隧道主沉管波浪荷载计算中，用Morison公式解析法与数值模拟的计算结果误差较小，采用Morison公式计算较为简单，适合在工程项目中推广使用。

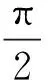
(3)在一般的工程条件下，速度力系数CD的取值、海洋生物生长厚度等因素对Morison公式计算结果影响不大；而惯性力系数Cm的取值和波浪相位差对计算结果影响较大，实际工程运用中应予重点关注。