感潮河段整治线宽度确定方法
肖烈兵,阮 伟
(1.中交上海航道勘察设计研究院有限公司,上海 200120;2.浙江大学,杭州 300058)
整治线宽度的概念来自于具有涨淤落冲规律的径流河道浅滩段航道整治,是指对应于整治水位的河宽缩窄度。相关研究已有半个多世纪,就其途径而言,大致可分为经验分析方法、水力学方法和河流动力学方法三大类。
1 问题的提出
经验分析方法是根据河道实测资料,找出优良河段河宽水深之间的关系,得到经验公式或确定方法,包括河相关系公式法、优良河段与浅滩段之间的河宽、水深比值关系法,以及优良河段河宽与断面平均水深函数关系法等三种,三种方法均是建立河道宽度与水深之间的经验公式,并且利用河道自身的资料确定公式中的系数,最终得到需要的航道水深与整治流量(或水深)相应的河宽。
水力学方法的基本出发点是以河道水力学为基础,联解有关水力学方程得到整治线宽度公式,如最普遍的方法就是联解明渠恒定均匀流的连续方程和阻力方程,并且基于整治后浅滩可重塑优良河段的断面形态的认识,引入河相关系式共同联解,或是假定浅滩整治前后通过的整治流量相等或相对平衡的(VJ)相等,同样将其与连续方程和曼宁公式联解,即可得到整治前后与整治流量相对应的河宽-水深关系式。
河流动力学方法在水力学方法的基础上,进一步考虑水流与河床之间的相互作用与变化,根据泥沙运动理论及河床演变的某些规律推求整治线宽度公式。其中还包含了根据河床变形计算法推求整治线宽度的方法,基于河道沿程输沙平衡或浅滩整治前后输沙能力平衡的方法,其中最有代表性和影响最大的是最后一种方法,其基本观点是:浅滩整治前后通过的流量不变,河道输沙能力不变,水位达到设计水位后水流停止造床。通过引入推移质泥沙或悬移质泥沙输沙率方程,与水流连续方程和阻力方程及河相关系式联立求解,最终同样得到整治前后与整治流量相对应的河宽-水深关系式。
显然,河流动力学方法无疑是理论上最为完整的,不仅考虑了浅滩整治前后通过的水流变化,而且也考虑了泥沙运动及其引起的河床变化,并在许多工程实践中得到应用和检验。虽然各种方法出发角度和基本点不完全相同,但最终都得出了如下的公式形式
其中系数A与指数y受来水来沙条件和河道水沙运动特性等多种因素的影响,并随着浅滩整治前后河床形态变化、主槽流量增减、床面粗化等因素而变化。
对于感潮河段,由于水沙动力因素与径流河道不同,上述方法的出发点和基本点虽不能完全符合实际情况,但仍具有参考借鉴的意义。国内外学者对此进行了研究,得到一系列经验或半经验的公式。窦国仁[1]假定“浅滩整治前后河道输沙能力不变”,推导出了整治线宽度的公式。张幸农[2]、张玮[3]从泥沙运动和河床演变角度,提出了冲积河流浅滩相应的整治线宽度公式。解中柱[4]采用多种方法相结合,结合浅滩的具体情况综合确定了宜宾至重庆段浅滩的整治水位和整治线宽度。乐培九、李旺生[5]引入沿程河床相对可动性为常数的假定,从沿程床沙动或不动的几率相同的观点出发,获得了冲积河流航道整治线宽度的理论公式。王秀英等[6]提出了适应不同类型浅滩整治的局部输沙模式及平衡系数确定公式,建立了能够适用于束窄河宽和调整断面水沙分配等不同形式建筑物整治线宽度确定的统一公式。国外A.Vanoni[7]、I.Jansen也提出了相关的河道整治原则。整治线宽度的计算还有许多公式可循[8-13],然而这些公式多是在某些特定条件下或引入假定求得,在应用时常使人难以取舍判断,且考虑潮汐因素的公式甚少,因此很有必要进一步加以研究。
2 潮汐河段整治线宽度确定方法
涨落潮流对于航道整治工程的作用往往呈现不同的有时甚至相反的作用。一般来讲,在径流较大、落潮流占优势的河口汊道,当在浅段布置整治建筑物后,航道范围内落潮流的单宽流量和输沙率增大,有利于浅滩冲刷和航道维护。因此,落潮水流经过整治工程后对航道有利,这一点与目前对径流较大的感潮河段和河口区采用落潮流进行整治相符。对于涨潮流,在整治初期,浅滩被冲刷,其部分泥沙将被携带至整治范围内的边滩区域,造成边滩上游地段的淤积。随着时间推移,上游航道和边滩淤积以及工程所带来的河道阻力的增大,将使得河道纳潮量减小,抵消了落潮流的整治效果。因此,在径流较大的感潮河段和河口区,增加河段的落潮动力往往是整治感潮河段的主要思路,而增加涨潮流对整治工程效果往往起着不利的影响。
整治感潮河段和河口所依据的是束水攻沙的原理,即通过增大整治线范围内的输沙能力,以达到冲深浅滩并维持航道断面。整治建筑物顶高程取最优整治水位时,累计的整治效果将达到最大值,即断面输沙能力达到最大值,此即为最大输沙能力法的原理[14]。此时,与最优整治水位相对应的水深即为此整治方案下的最大整治水深。由于整治前后输沙能力的变化和水深变化是相辅相成的[15],因此最大输沙能力可通过最大水深来反映,而最大输沙能力又需要在最高整治水位和相应整治线宽度前提下进行计算,因此可将最大输沙能力作为最大水深和整治水位、整治线宽度之间相互联系的桥梁。由此通过对最大水深的计算,即可得出最优整治水位和相应整治线宽度之间的关系。最后,在河道断面整治水位已知的前提下,即可得出此处相应的整治线宽度。
下面通过最大输沙能力法具体分析最优整治水位与整治线宽度之间的关系。
在图1中,对于无潮河流,整治水位z越高(不超过最高洪水位),整治建筑物(b区域)所拦截的输沙量越多,整治线内(B区域)累积增加的输沙能力也越大,整治效果也就越好。
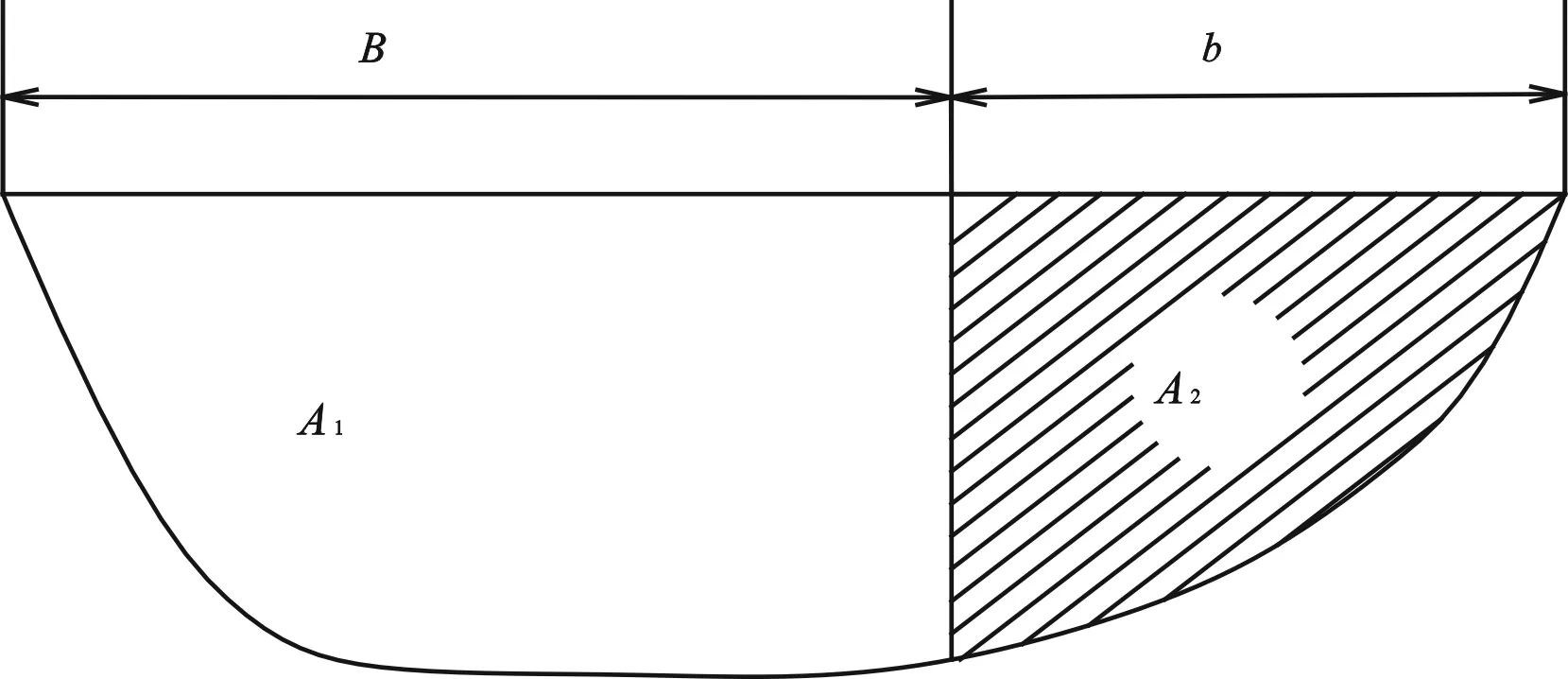
图1 整治断面示意图Fig.1 Section of waterway regulation engineering
在感潮河段和河口处,水流为径流和潮流的相互作用,潮流呈周期性变化,相应的输沙能力也在不断的变化,整治建筑物虽然增加了落潮输沙率,但也在一定程度上增加了涨潮输沙率。在感潮河段和河口处,整治所利用的是落潮流的作用,因此须将由涨潮流引起的不利因素在落潮流因素中进行抵消。
由于泥沙等介质在输运时会占用到该水位以下的过流断面,因此在研究某一水位的输沙能力时,根据断面地形资料及足够长的水位、流速(或流量)、含沙量等资料,计算不同水位下河道断面在一个潮周期内累积通过的输沙量。根据整治河道断面的水位、垂线含沙量及流量的实测资料,分别描绘出整治断面的涨、落潮输沙量随水位变化的实测点,进一步拟合出涨、落潮输沙量随水位变化的累积函数Wu(z)、Wd(z),其分别为全断面的涨、落潮输沙量函数。
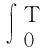
H=c1W1/2
(1)
式中:H为水深,c1为系数,W为输沙量。
整治工程进行后,相应增加的水深Hz为
Hz=c1[W1d(z)+△W(z)]1/2-c1W1d(z)1/2
(2)
式中:W1d(z)为整治线范围内整治前的过输沙量函数,△W(z)为边滩b区域内的综合过水量函数,即假定涨潮流的不利影响在落潮流中扣除。
若要使整治效果最优,即要获得最大的整治水深,则dHz/dz=0,可得
(3)
在潮汐河口浅滩或海港进口航道浅段,河道断面基本为宽浅型,断面深槽与边滩之间无明显分界。假定流量、含沙量沿断面分布较均匀。在边滩范围b区,由于总的过潮量较小,因此涨潮流的不利因素不能忽略。而在整治线范围B区,由于断面总流量较大,因此涨潮流因素可近似忽略,基于此可假设扣除涨潮流不利因素之后的潮量与扣除前的潮量比值为C(C可通过断面实测资料获得)。基于以上分析,即有
(4)
将式(4)代入到式(3)中整理得
(5)
设λ=(B+b)/B为缩窄系数,将其代入式(5)中可得
(6)
则式(6)即为根据输沙量与水位曲线确定出的整治水位和整治线宽度的关系式。
3 典型潮汐河段整治工程案例
本文选取长江下游福姜沙河段双涧沙北侧航道SJS1#断面作为较详细的计算案例,并以长江南京以下12.5 m深水航道一期工程白茆沙河段整治工程和长江口深水航道治理工程这两项成功的航道整治工程作为核算案例。
SJS1#断面位于双涧沙北侧航道,宽度约1 900 m,受上游径流和涨落潮流的影响。该处设有青龙港上游水文站,因此该断面有水位、流量和含沙量等较丰富的水文资料。根据2012年11月29日11时~11月30日15时一个潮周期内的水位、流量和含沙量沿垂线分布实测资料,分别拟合全断面的涨、落潮输沙量与潮位的相关关系,拟合图见图2、图3,拟合函数Wu(z)、Wd(z)为
Wu(z)=-10 303z3+72 472z2-170 727z+133 843
(7)
Wd(z)=3 673.2z3-20 739z2+39 444z-6 072.4
(8)
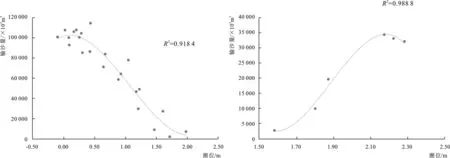
图2 落潮输沙量与潮位的关系拟合图 图3 涨潮输沙量与潮位的关系拟合图Fig.2 Relationship between ebb tide sediment transport and tidal level Fig.3 Relationship between flood sediment transport and tidal level
将式(7)、(8)代入式(6)中进行整理。根据感潮河段整治水位计算公式求得该断面处整治水位为1.3 m,因此z值相应取为1.3。根据涨落潮资料分析,此处C值取0.92。将z值和C值代入到整理后的公式中,即可求得λ=1.33。由SJS1#断面处河宽约为1 900 m,可最终求得整治线宽度B=1 429 m。
进一步对白茆沙河段、长江口北槽进行实例验证。分别取白茆沙河段荡茜口位置、长江口北槽S1丁坝位置和双导堤出口作为计算断面,位置见图4、图5。
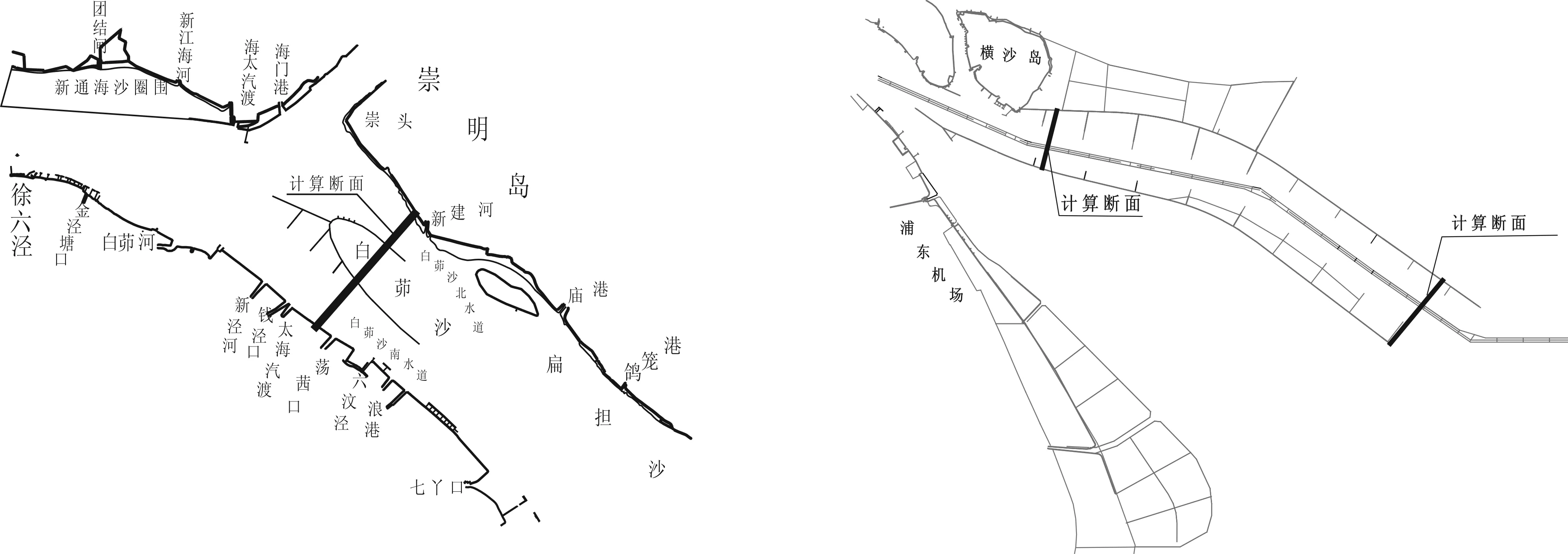
图4 白茆沙河段计算断面示意图 图5 长江口北槽计算断面示意图Fig.4 Calculation section of Baimaosha river Fig.5 Calculation section of north channel of Changjiang estuary
根据实测水位、流量和含沙量资料,整治水位取建筑物实际高程,按最大输沙能力法计算得北槽和白茆沙整治线宽度,结果见表1。由表1可见,计算值与实测值非常接近,证明本文所提出的感潮河段整治线宽度计算方法是可行的。

表1 整治线宽度计算值与整治工程高程对比Tab.1 Comparison between the calculated width of regulation line and the elevation of regulation project m
4 几点讨论
4.1 方法的适用性
本文中整治线宽度计算方法是对于感潮河段来建立的,对于单向径流河道不适用。由于公式中必须考虑落潮和涨潮水流分别对河床的作用,当无涨潮流时公式无法建立。
4.2 整治线宽度和整治水位相互关联
整治水位与整治线宽度是一个组合,当整治水位取值较高,整治线宽度也相应较大,反之则较小。显然,对满足某一航道整治目标而言,可以有多种不同的整治水位和整治线宽度组合。在工程实践中,由于整治参数取值不合理,整治工程难以发挥作用,航道整治目标难以实现。有时航道尺度虽然可达到要求,但整治水位取值较大引起局部过度冲刷,危及整治建筑物安全或导致流态恶化。有的工程造价过高,造成工程浪费。
为此,整治线参数的确定一般先行确定整治水位,然后根据整治水位计算整治线宽度。对于天然河流整治水位的含义一般是此水位对应的流量造床作用最大,因而当退水期水位降落到整治水位附近时,整治建筑物开始起到束导水流冲刷河床的作用,冲刷作用的时间主要集中在整治水位降至设计水位的时段。因而,在实际工程中考虑局部冲刷、工程影响、工程造价等多方面因素,整治建筑物高程一般略低于实际计算的整治水位。在其值确定以后代入前述公式计算出整治线宽度,一般情况下结合数物模型研究反复调整不同的整治水位和整治线宽度组合,以求达到最优的整治建筑物布置。
4.3 守护工程不存在整治参数的计算
感潮河段整治水位是对应于造床流量的水位,有一个较大的变动范围,尤其是在受潮流影响明显的河段。鉴于感潮河段航道整治通常是采用以控制河势变化或稳定洲滩格局为主的守护工程措施,一般是以低矮的护滩、护底潜堤、软体排为主,辅以护岸工程措施,以避免对河道防洪和建筑物局部冲刷造成不利影响。因此,感潮河段守护工程的高程与整治水位脱离了直接的相关关系,整治参数的计算基本没有实际意义。
5 结论
本文基于感潮河段水沙运动分析,从增加落潮输沙量的角度出发提出整治线宽度计算方法,该方法充分考虑到潮汐因素的影响,在感潮河段或者河口具有较好的适用性。提出的最大净输沙能力法计算整治线宽度的方法在一定程度上丰富了航道整治理论。工程设计中可以此潮汐河段整治参数计算方法为基础,利用数学模型和物理模型等试验手段进行深入研究,顺应河势、因势利导,合理布置整治建筑物,从而达到维持或改善航道航行条件的目的。

