基于Monte Carlo方法计算积分的研究

汪 楠

（江西医学高等专科学校，江西 上饶 334000）

引 言

上世纪40年代美国在研制原子弹的“曼哈顿工程”时，由乌拉姆和冯•诺伊曼首先提出蒙特卡罗方法。数学家冯•诺伊曼用赌城Monte Carlo—来命名这种方法，为它蒙上了一层神秘色彩[1]。1777年，法国数学家布丰用投针实验的方法求圆周率π，这被认为是蒙特卡罗方法的起源。蒙特•卡罗方法（Monte Carlo method），也称统计模拟方法，使用随机数（或伪随机数）来解决计算问题的方法。

可以利用蒙特卡罗方法预测误差统计量，解决扩展卡尔曼滤波器中近似误差协方差方程，可消除由于误差协方差方程中过于简化的闭合，而导致的在扩展卡尔曼滤波器中发现的无穷大误差增长[2]。在生物遗传方面，在蒙特卡罗模拟中引入理想组织等效正比计数器，并结合微剂量动力学模型精确计算重离子生物有效剂量[3]。在数学方面，根据蒙特卡罗方法可用来计算反常积分[4]。在与计算机结合方面，通过建立改进提升决策树的近似模型，运用算法合成新样本点信息，然后采用蒙特卡罗方法预测，进行可靠性分析，可以得出利用蒙特卡罗方法改进梯度提升决策树进行可靠性分析[5-7]；在生物学方面通过构建薄膜的三维生长动力学模型[8]，实现了薄膜生长的数值模拟,可以得到了沉积速率、基底温度和原子覆盖度等因素对薄膜表面粗糙度的影响。在天气气象方面利用蒙特卡罗方法推求降水分布[9]，采用K-S检验对模型进行显著性检验，采用基于欧氏距离的层次聚类方法进行状态划分，可以确定了原州区的降水分布[10]，建立了适用于原州区的滑动平均加权马尔可夫预测模型。蒙特•卡罗方法在金融工程学[11-12]，宏观经济学，计算物理学（如粒子输运计算、量子热力学计算、空气动力学计算）等领域应用广泛。

1 蒙特卡罗方法方法原理

蒙特卡罗方法又称随机抽样方法或者随机数法，蒙特卡罗方法是一种非常重要的数值计算方法，它是建立在以概率统计理论为基础的一种方法。蒙特卡罗方法通过计算机随机数模拟仿真来解决问题，同时可以通过模拟来检验模型的正确性。

1.1 基本原理

一个事件的概率可以通过大量实验中的事件频率来估计，事件的概率可以通过事件的频率来表示，这个已经通过大数定理进行了证明，蒙特卡罗分析就是基于该理论。对影响事件可靠性的随机变量进行大量随机抽样，然后将抽样结果代入已知的功能函数式，分析结果是否有效，最后得到结果的有效概率。

有一组独立的随机变量为Qi(i= 1,2,3…)，而这组随机变量对应的概率密度函数分别为Yq1,Yq1,Yq1…，对应的功能函数式为F=g(q1，q2，q3…)。根据随机变量的分布，产生一组随机数q1，q2，q3，q4…，每个随机数对应的功能函数的函数值为Fi=g(q1,q2，q3，q4…)(i= 1,2,3…)，并将Fi记录下来产生一个新的数组，那么n趋于无穷大时时，根据伯努利大数定理及正态随机变量的特性得出所需要的结果即结构失效概率和可靠指标。

1.2 蒙特卡罗方法的步骤

1) 构造概率过程；一些事件的本身就是具有随机性质的问题，比如分子的运动、原子的碰撞和粒子的运输问题等，对这类微观方面的问题，主要工作是描述和模拟分子运输和运动的概率过程。对于一些确定性非随机性质问题，例如数学中的定积分的计算，需要构造一个的概率过程，它的某些参数就是所求问题的解。将无随机性问题转化为随机性问题。

2) 将已知概率进行分布抽样；建立概率模型后开始试验，因为概率模型是可以看作是由概率分布构成的，所以会产生的概率分布的随机变量，这个随机变量就是实现蒙特卡罗方法的过程。

3) 建立恰当的估计量。构造概率模型，根据模型进行抽样，即进行模拟实验，所求随机变量的值是解的无偏估计。建立各种估计量，就是对模型模拟实验的结果和数据进行观察和记录，从数据中找出所需要的结果。

2 蒙特卡罗方法在积分的应用

蒙特卡罗解决微积分的核心问题就是求解这个随机变量的期望值，无论这个积分函数是连续分布还是离散分布。按所需要的概率分布进行采样，采样次数为N，当N→+∞时，所求的这个期望值为E(X)，随机变量连续性和离散型的期望值分别为

2.1 定积分的计算

假设f(x)是在(x1,x2)上连续有界可积的函数，且0≤f(x)≤p，求定积分

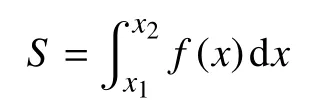
因为f(x)是非初等函数，无法推导出其原函数，即无法用常规的方法求解。在此处，将其按麦克劳林公式展开：

可以求出：

用蒙特卡罗方法通过计算机进行计算该积分。开始向该矩形区域随机投点，投点的总数量为N，落在曲线下方X轴上方的点的数量为n。该矩形区域的面积为Q=3×1=3。很容易理解，随机投掷的点落在函数下方发生的概率为定积分的值除以区域总面积，则S=nQ/N。

如图1所示，当投点数N= 100时，处于曲线下方的点的数量为n= 43，则，数据偏差为3.594%。

图1 N = 100时试验图

如图2所示，当投点数N= 1000时，处于曲线下方的点的数量为n= 438，则，，数据偏差为1.80%。

图2 N = 1000时试验图

如图3所示，当投点数N= 10 000时，处于曲线下方的点的数量为n= 4428，则1.3284，数据偏差为0.724%；从实验结果可以看出，投的点数N越大，得到的数据更接近真实值，那么可以得出结论：当N→∞时，实验得出的结果就等于真实值，数据的偏差趋于0。

图3 N = 10 000时试验图

在（3，5）之间，取n个随机数，计算出这n个数的平均值。平均值可以近似等于g(x)在(3，5)之间的数学期望E[g(x)]。即有

编写程序代码，由计算机随机生成n个随机数，当n取1000时，多次运行程序得到运行结果近似等于40.5。

2.2 计算二重积分

在(1,4)范围内取n个x的随机数，在(2,5)范围内取n个y的随机数，g(x,y) 为(x,y)所对应的函数值，求出所有g(x,y)的平均值，可以近似于g(x,y)在x∈(1,4),y∈(2,5)之间的数学期望E[g(xy)]，代入公式，可得：

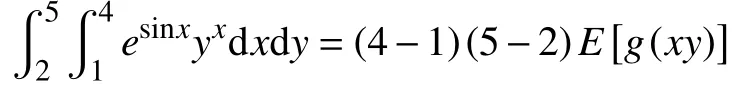
采用蒙特卡罗法编程计算，当n取1000时，该二重积分的值约为217.6。

3 结 论

随着计算机技术的快速发展，蒙特卡罗方法被广泛应用于各个行业中。由于现代计算机的软硬件计算成本降低，在使用蒙特卡罗方法时，可以增大实验模拟次数，从而减少计算误差，得到更精确的值。