主动电磁轴承飞轮转子系统自适应偏置控制

刘宇轩，吴国辉，陈亮亮

（南昌航空大学 信息工程学院，南昌 330063）

引 言

高速飞轮储能系统具有使用寿命长、储能密度高、高效率、无污染等优点，是一种具有广泛发展前景的电能储存方式[1-3]。主动电磁轴承具有动力特性可控、无机械接触、寿命长、损耗低、无需润滑等优点，是高速飞轮储能系统中最常用的转子支承结构[4-6]。主动电磁轴承常采用差动控制方式，即在同一个自由度上有两个对置的磁铁在同时工作，这两个电磁铁具有相同的恒定偏置电流，偏置电流与控制电流进行差分运算后再分别驱动两个电磁线圈。这种差动布局使得正向力和负向力都能产生，有利于改善电磁轴承系统的动态性能。由于恒定偏置电流的存在，即便是控制电流为零时电磁轴承也存在一定电能损耗。为减小偏置电流产生的电能损耗，国内外学者做了一些研究工作。Brown等[7]和Ishida等[8]分别研究了电磁轴承零偏置控制方式，并通过试验验证了算法的有效性。Johnson[9]在博士论文中也研究了零偏置和低偏置控制方式。Hu等[10]提出了一种最优电流分配的低偏置控制方法。Sahinkaya等[11]研究了节能最优的变偏置电流控制方法。这些算法能够通过较低的偏置电流实现电磁轴承转子系统的稳定悬浮，节约了电能，但算法较为复杂，实现困难。

本文研究了一种自适应偏置差分控制方法，首先介绍了算法的基本原理，然后利用控制理论分析了该方法的稳定性，最后通过仿真验证了该算法的控制性能，详细分析了电磁轴承飞轮转子系统在阶跃信号及正弦信号扰动下转子的运动轨迹和电磁轴承线圈的电流特性。

1 电磁轴承飞轮转子系统模型

图1为简化后的立式四自由度电磁轴承刚性飞轮转子系统结构，主要由飞轮转子、一体化电动机/发电机、电磁轴承、保护轴承以及位移传感器等部分组成。整个系统轴向采用永磁支撑，2个电磁轴承用于径向悬浮，4个电涡流传感器测量分别测量飞轮转子在四个自由度上的位置信号。

图1 主动电磁轴承飞轮转子系统原理图

图1中，oxyz坐标系的坐标原点位于飞轮转子的质心c点，z轴在两径向轴承中心连线上，x、y与z构成右手坐标系。lsA和lsB分别为传感器A和B的中心到质心c的垂直距离；lbA和lbB分别为径向电磁轴承A和B的中心到飞轮转子质心c点的垂直距离[12]。

在工程实际中，对飞轮转子系统的四个自由度常采用单独控制方式，其原理如图2所示。图2中，控制器实时读取位置传感器测量的位置信息，经过控制算法处理后输出控制信号，功率放大器对控制信号进行放大，驱动电磁轴承线圈，产生控制飞轮转子位置的电磁力。

图2 单自由度电磁轴承控制系统

功率放大器和位置传感器的传递函数可近似为一个比例系数k。单自由度电磁轴承飞轮转子系统的运动方程可表示为[13]：

式中，m为转子质量，y为转子的位移，fy为电磁轴承产生的控制电磁力，电磁力的表达式为：

ks和ki分别为力−位移系数(位移负刚度系数)及力−电流系数，根据式(1)和式(2)，可得到电磁轴承飞轮转子系统的传递函数为：

式中，Y(s)和I(s)分别为转子位移y和控制电流ic的拉普拉斯变换式。由式(3)可知，电磁轴承飞轮转子系统传递函数包含一个位于右半平面的极点，系统不稳定，因此需要施加外部的主动控制力。

2 差动控制方式电磁力模型

单自由度电磁轴承飞轮转子系统差动控制方式原理如图3所示。对置的两块电磁铁产生的电磁吸力共同作用于转子，使转子在某个方向上保持受力平衡。对置的两电磁铁线圈具有相同的偏置电流，在同一时刻，当一个线圈的驱动电流为偏置电流与控制电流之和时，另一个线圈的驱动电流则为偏置电流与控制电流之差，即，

图3 电磁轴承差动工作方式

式中：i1和i2分别为对置电磁线圈的驱动电流，I0为偏置电流，ic为控制电流。

在图3所示的差动工作方式下，电磁轴承产生的电磁力为：

式中，µ0为真空中磁导率，Aa为磁极面积，N为线圈匝数。

当转子在平衡位置(y= 0，ic= 0)作小位移扰动时，若将式(2)在平衡点附近用泰勒级数展开并省略二阶无穷小以上的量，即：

式中：fy(y=0,ic=0)=0，，。

故有：

式中,ks=分别称为力−位移系数(位移负刚度系数)及力−电流系数。

在传统的差动控制方式中，偏置电流I0是恒定值，且远大于控制电流ic，由于恒定偏置电流的存在，即便控制电流很小，轴承线圈也会产生一定的损耗。

3 自适应偏置差动控制

3.1 自适应偏置差动控制基本原理

自适应偏置差动控制方式的基本思想为：偏置电流随控制电流的变化而变化，且偏置电流的大小为控制电流的绝对值，即：

在自适应偏置差动控制方式中，同一时刻对置的两个电磁线圈中只有一个线圈有电流，其值为控制电流的两倍，而控制电流往往远小于传统差分控制方式下的恒定偏置电流，因此自适应偏置差分控制方式下线圈的驱动电流较小，可以降低轴承的电能损耗。

3.2 稳定性分析

电磁轴承飞轮转子系统常采用分散PD控制器，对飞轮转子系统的各个自由度进行单独控制，则问题可简化为对4个单自由度磁悬浮系统进行控制。单自由度电磁轴承转子系统的传递函数如式(3)所示。

PD控制器的传递函数为：

式中，d为微分系数，p为比例系数。PD控制的系统框图如图4所示。

图4 PD控制原理图

电磁轴承PD控制的闭环传递函数为:

式中，pki+ks称为电磁轴承系统净刚度。由控制理论可知，控制系统稳定的条件是净刚度大于零。

自适应偏置差分控制方式中位移负刚度系数ks和力−电流系数ki分别为：

由式(10)、式(11)可知，当p>|ic|/C0时净刚度pki+ks大于零，系统就是稳定的，因此可以通过调节比例系数p使主动电磁轴承飞轮转子系统保持稳定。调节d使系统获得足够的阻尼，从而使闭环控制系统保持稳定并达到期望的控制性能。

4 仿真分析

本节将对比传统差动控制方式和本文的自适应偏置差动控制方式的控制性能。分别将传统的差分控制方式和自适应偏置差分控制方式应用于如图1所示四自由度主动电磁轴承飞轮转子系统中，飞轮转子的参数如表1所示。

表1中，m为飞轮转子的质量，Jx及Jy分别为转子绕x及y轴的转动惯量，Jz为转子绕z轴的转动惯量。kiA和kiB分别为径向电磁轴承A和径向电磁轴承B的力−电流系数；ksA和ksB分别为径向电磁轴承A和径向电磁轴承B的力−位移系数。

表1 飞轮转子参数

电磁轴承分别采用传统的差分控制方式和自适应偏置差分控制方式对主动电磁轴承飞轮转子系统进行仿真研究，控制方法为分散PD控制。在传统差分控制方式中，偏置电流为1 A。系统仿真过程中，飞轮转子静态稳定悬浮，在0.2 s时上端Y方向的参考位置由0变为30 μm，图5为传统差动控制方式和自适应差动控制方式响应曲线图。图中红色曲线为自适应偏置差分方式的阶跃响应曲线，绿色曲线为传统差分控制方式的阶跃响应曲线。可以看出，传统差分控制方式的上升时间和调节时间要略短于自适应偏置差分算法，但自适应差分控制方式具有更小的超调量。总的来说，传统差分控制方式的控制性能要略好于自适应差分控制方式。

图5 两种控制方式下的阶跃响应曲线

图6为系统阶跃响应过程中传统差分控制方式Y方向2个线圈中的电流。图7为自适应偏置差分控制方式Y方向2个线圈中的电流。

图6 传统差分控制方式Y方向对置线圈中的电流

图7 自适应偏置差分控制方式Y方向对置线圈中的电流

可见，在整个阶跃响应过程中传统差分控制方式的正反两个线圈都有驱动电流，两线圈的电流值都以偏置电流为中心波动；而自适应偏置差分控制方式下的正反2个线圈在同一时刻只有一个线圈有驱动电流，且驱动电流为控制电流的两倍。在传统差分控制方式中，偏置电流为1 A，阶跃响应稳定后的控制电流不到0.1 A，偏置电流要远大于控制电流。在自适应偏置差分控制方式中，同一时刻只有一个线圈有驱动电流，且驱动电流的值很小，阶跃响应稳定后的线圈驱动电流还不到0.004 A。磁轴承线圈中损耗的功率为：

式中，P为每个轴承线圈损耗的有功功率，i为线圈电流，R为线圈电阻。式（10）表明，磁轴承线圈中的电能损耗与电流的平方成正比，由于自适应偏置差分控制方式本的线圈电流远小于传统差分控制方式，因此自适应偏置差分控制方式能够有效节约电能。

为进一步研究自适应偏置控制方式的控制性能，当飞轮转子静态悬浮时在上磁轴承X方向的控制电流中注入一个余弦扰动，Y方向的控制电流中注入一个正弦扰动，扰动电流的频率为10 Hz，幅值为0.05 A。图8、图9为存在正弦电流扰动时传统差分控制方式下飞轮转子上端和下端的轨迹图，图10、图11则为自适应偏置差分控制方式下飞轮转子上下端的轨迹图。

图8 正弦扰动下传统差分控制方式飞轮转子上端轨迹图

图9 正弦扰动下传统差分控制方式飞轮转子下端轨迹图

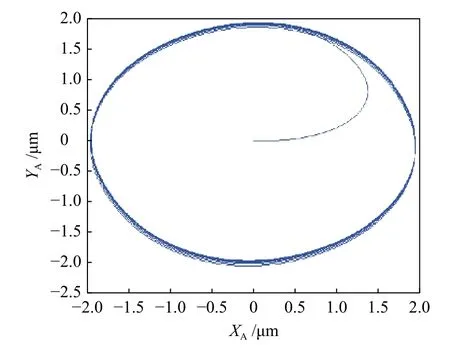
图10 正弦扰动下自适应差分控制方式飞轮转子上端轨迹图

由图8~图11可以看出：在外界正弦扰动下，传统差分控制方式和自适应偏置控制方式都能使飞轮转子系统保持稳定，扰动电流引起的振动幅值小于2微米。在相同的正弦扰动下，传统差分控制方式的转子振幅要略小于自适应偏置控制方式，但相差不大。在正弦扰动下，传统控制方式和自适应偏置控制方式Y方向两对置轴承线圈的电流曲线分别如图12、图13所示。

图11 正弦扰动下自适应差分控制方式飞轮转子下端轨迹图

由图12、图13可以看出，与阶跃响应时的电流曲线类似，传统差分控制方式的轴承线圈电流依旧远大于自适应差分控制方式的线圈电流。因此，自适应差分控制方式的轴承线圈损耗较传统差分控制方式要小得多。

图12 传统差分控制方式Y方向对置线圈中的电流

图13 自适应差分控制方式Y方向对置线圈中的电流

5 结 论

通过本文的理论分析及仿真研究，可以得出以下几点结论：

1) 本文提出的自适应偏置差分控制方式能使主动电磁轴承飞轮转子系统保持稳定，具有结构简单，易于实现的特点。

2）本文提出的自适应偏置差分控制方式能够有效减少电磁轴承线圈中的电流，节约电能，且具有与传统差分控制方式相近的控制性能。

3）自适应控制算法的部分动态控制性能较传统的差分控制方式略差，其阶跃响应的上升时间和调节时间要略长于传统差分控制方式，抗外界扰动能力也略差。