浅谈中心极限定理

夏文文 河南财经政法大学

一、引言

中心极限定理在概率论中有着极其广泛的应用背景。提到中心极限定理，要先介绍一位叫棣莫佛的数学家，虽然出生在法国，但他却在32岁时成为英国皇家学会会员。他在1718年首次出版的《机遇论》被称为概率论史上有三部里程碑性质的著作之一。1712年，一位叫亚历山大的人向他提出了一个关于赌博的问题，最终他给出了二项分布下每局获胜概率p=0.5的证明。但是当局数n很大时，计算就变得非常困难。因此棣莫佛就找到了一个近似的算法，它就是后面我们所熟知的“二项分布的正态近似”。因此可以说棣莫佛的工作在数理统计的发展史上有着里程碑式的意义。

在实际生活中，有些现象会受到很多相互独立的因素的综合影响，如果每个独立因素的影响都非常小，单独来看的话并不好研究，但如果放在一起的综合影响近似服从正态分布。在研究中经常需要考虑研究对象受许多相互独立的随机因素的综合影响。比如在射击时，子弹命中的位置偏离目标位置的程度，就受到很多随机因素（如空气阻力、风向、射击所用枪支的结构等）的综合影响。同时，许多研究结果表明，受到这些许多综合影响的随机变量近似服从正态分布。

二、什么是中心极限定理

在统计学中，想要研究某个总体的某种指标，如果这个总体很大，通常都是通过从该总体中用某种方法抽取一定的样本，然后根据抽样得到的样本结果来估计该总体的情况。但样本毕竟是样本，它和总体之间还是有一定差别的。所以我们通常还要根据抽样结果，计算出相应的置信区间，这样会更具有说服力。除此之外，我们往往还会进行假设检验，将样本值和假设值进行比较，以此来判断我们所作的假设是否正确。

但是，想要获得置信区间或者进行假设检验，都必须知道样本的分布属于哪一种类型。如果我们连样本的分布类型都不知道，相应的统计量我们也就不可能知道，更不可能求出置信区间或者进行假设检验。但还好我们有伟大的数学家，他们发现的中心极限定理帮我们解决了这一难题。

在实际中，许多问题的研究都需要求n个独立同分布随机变量和的分布函数Fn（y），当n很大时，大多数情况下寻求准确的Fn（y）是很难的。而中心极限定理的思想对求解Fn（y）提供了很大的帮助，我们可以用极限的方法求Fn（y）的近似分布。我们习惯上把概率论中有关论证大量独立随机变量的和近似服从正态分布的这一类定理统称为中心极限定理。

三、两个常用的中心极限定理

下面给出了在概率论中两种常用的中心极限定理的主要内容和它们之间的关系。

（一）林德贝格——列维中心极限定理

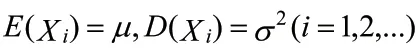
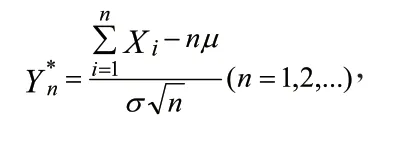
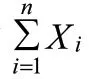
从这个定理我们可以看出，独立同分布随机变量的共同分布不管是什么分布，只要共同分布的方差存在，且不为0，那么大量该随机变量和的分布就近似为正态分布。

（二）拉普拉斯中心极限定理

设随机变量Xn服从于二项分布B（n，p），n=1，2，…，则

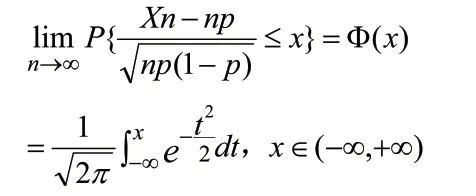
通过该定理可以知道，当n充分大（n 30）时，服从二项分布的随机变量Xn近似服从于正态分布，期望为np，方差为np（1-p）。

这个定理是最早的中心极限定理，它是用正态分布近似计算二项分布的一种方法，因此被称为“二项分布的正态近似”。当n很大时，二项分布随机变量的计算结果就会非常大，利用“二项分布的正态近似”的思想使问题变得简单化。除此之外，我们还常用到“二项分布的泊松近似”，它们之间还是有一定的区别。比如，当p很小，而np又不太大时，我们常用泊松近似；当np和np（1-p）都比较大，一般认为np＞=5和np（1-p）＞=5时，就可以用正态近似。

当使用“二项分布的正态近似”时，往往需要修正，合理的修正可以提高精确度。设Xn～B（n，p），如果满足np＞=5和np（1-p）＞=5，那么二项分布的正态近似的公式为：

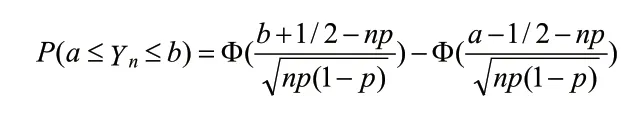
（三）两个中心极限定理的关系

拉普拉斯中心极限定理其实就是随机变量序列独立同二项分布情形下的林德伯格中心极限定理。前者要求随机变量序列服从于二项分布，而后者则是要求独立同分布即可。

四、中心极限定理的重要性质

1.当样本容量或实验次数n很大时（一般n＞=30），随机变量和的分布近似服从正态分布。随机变量和的均值为nμ，随机变量和的方差为nσ2，σ为总体标准差。

2.当样本容量或实验次数n很大时，独立同分布随机变量的算术平均值 的分布近似为正态分布。其中样本均值的期望与总体均值相等，而方差等于总体方差除以样本容量。

五、中心极限定理的在生活中的应用

中心极限定理在实际中的应用也是十分的广泛。保险这个行业对我们来说并不陌生，它是降低因意外事故造成损失的保障。保险的赔付一般都是比较大额的，那么就会有人好奇保险公司什么情况下会发生赔本呢？它赔本的概率有多大呢？

实例：某家保险公司年初有5000个同龄同阶层的人投保，并且已知该类人在两年内会出现重大意外事故的概率为0.005。该保险公司规定每个投保人都要在第一年的年初缴纳2000元作为保险费，而在意外事故死亡后其所填受益人可以从保险公司得到20万元。问在该保险公司的投保活动中，该公司将有多大的概率会赔本？

在投保中记第k个人在两年内意外身亡为“Yk=1”，否则为“Yk=0”，那么该随机变量服从二点分布B（1，0.005）。该保险公司在第一年年初可以收到保险费5000*2000=10000000元，所以当两年内死亡人数超过50人时保险公司才会赔本。各Yk为独立同分布的随机变量，E（Yk）= 0.005，D（Yk）=0.005*（1-0.005）=0.004975，由修正后的“二项分布的正态近似”公式可得：

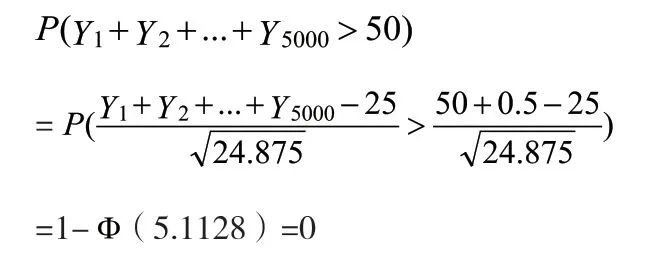
由此可见，该保险公司赔本的概率近似为0。这也就解释了保险市场新的公司不断萌发的原因。尽管如此，一份保险对我们来说还是十分必要的，在你生活困难时，它于你是雪中送炭；在生活美满时，它于你便是锦上添花。

六、中心极限定理的作用

中心极限定理的主要作用可以总结为以下三个方面：

（一）用样本来估计总体

当我们在没有办法知道总体所有数据的情况下，总体的分布显然也就无法得知。我们可以用样本的值来估计总体相应的值。在收集到了随机抽取的样本数据之后，我们可以计算出样本的平均值和标准差，由中心极限定理的性质，我们也就可以计算出总体的平均值和标准差。

（二）根据总体的平均值和标准差，判断样本是否来自于该总体

如果我们知道了某个总体的具体信息，并且知道某个样本的数据，我们就可以利用中心极限定理的性质，计算出样本来自于该总体的概率。如果所得的概率非常低，我们就可以确定样本不属于该总体。

（三）求未知非正态分布的置信区间

在大样本的情况下，要想求得未知分布的置信区间，就需要用到中心极限定理的内容。即可以利用正态分布的性质来求解出该未知分布的置信区间。

七、中心极限定理的意义

正态分布在概率论中占有着举足轻重的地位，它是许多概率和分布的理论基础。很多随机变量的分布都与正态分布有关系，比如我们所熟知的t分布、卡方分布、F分布等等。除此之外，在一些相关性检验中我们也能发现正态分布的身影，比如Pearson相关系数检验的前提条件就是该检验只能在正态分布的假定下进行，而Spearman秩相关检验和Kendall τ相关检验都用到了大样本下的正态近似。而中心极限定理则可以将大量随机变量和的分布最终归到正态分布的阵营之中，由此可见它在概率论和数理统计中有着非常重要的作用。

其次，中心极限定理还为概率论和数理统计在统计学的应用奠定了理论基础。在统计学的研究中，由于直接研究总体的特征比较困难，我们常常用抽样的方式进行研究，用某种方法和规则从总体中抽选一定的样本，并根据样本的某些指标来估计总体。但这个关键是要知道样本的分布，然而很多时候样本的分布都是未知的。中心极限定理指出只要样本容量n足够大时，未知总体的样本分布就近似为正态分布。因此，只要得到足够多的样本统计数据，就可以用正态分布的性质来处理。因此就可以利用中心极限定理把数理统计中的一些方法应用到统计学中。