深层高压页岩气藏吸附气含量评价新方法

赵玉龙 刘香禺 张烈辉 张 鉴 常 程 赵圣贤 张 帆

1. “油气藏地质及开发工程”国家重点实验室 西南石油大学 2. 中国石油西南油气田公司页岩气研究院

0 引言

页岩气赋存方式特别，包括游离气、吸附气和溶解气3种形式[1-3]，其中吸附气含量最高可达85%[4-5]，是页岩气的重要组成部分。广阔的勘探开发前景鼓励了页岩中吸附气含量的研究，相关工作对页岩气藏储量评估和开发方案制定等至关重要，是实现页岩气藏经济高效开发的基础和前提[6-8]。

页岩中吸附气含量的测定手段主要包括测井解释、现场解吸测试、分子动力学模拟以及等温吸附实验等。其中，测井解释需要用温度、压力等参数对吸附气含量经验关系式修正从而导致其精度不高[9]；现场解吸测试在岩心取出过程中损失气量难以准确计算[10]；分子动力学模拟结果的准确性还有待于检验[11]。因此，等温吸附实验便成为测定页岩中吸附气含量的主要手段。通过等温吸附实验可以获得特定温度、压力下甲烷在页岩中的吸附气含量，结合等温吸附模型拟合离散实验数据点可以获得页岩中吸附气含量随温度、压力变化关系式[12]。需要注意的是，学者们发现实验直接获得的吸附数据为过剩吸附量，不能代表页岩真实吸附情况，需要将其校正为绝对吸附量[13]。

学者们基于室内等温吸附实验开展了大量研究工作，大体上可分为以下4类：①设计对比实验研究页岩中吸附气含量影响因素，如温度、压力、有机质含量（TOC）、热成熟度（Ro）、黏土矿物含量等；②结合室内等温吸附实验评估目标区块页岩储层吸附能力及热力学特征等；③围绕等温吸附模型优选及改进开展相关研究工作；④针对实验测得的过剩吸附量开展校正研究工作。其中，关于等温吸附模型改进和过剩吸附量校正的研究尤为普遍。等温吸附模型可分为单分子层或多分子层模型、基于吸附势理论的微孔充填模型、简化局部密度理论吸附模型、Ono-Kondo吸附模型以及上述各种模型的组合模型等[14-16]。目前，当以Langmuir等温吸附模型应用最为广泛，究其原因可大体概括为两点：①Langmuir等温吸附模型形式简单，仅用双参数即可较好地拟合吸附实验数据；②早期等温吸附实验压力较低，所得实验数据点呈现很好的Ⅰ型吸附曲线特征[17]，尤其是煤和活性炭等吸附气含量较大的样品在低压段难以观测到吸附气含量最大值，此时Langmuir等温吸附模型拟合精度很高。随着实验设备的升级，研究者们在高压下观察到了吸附气含量随压力升高而下降的现象[18-26]，显然单调递增的Langmuir等温吸附模型不适应高压下降段的描述任务。此外，值得注意的是Langmuir等温吸附模型假设气体为单分子层吸附且吸附位均匀分布，吸附气体分子间无相互作用力[17]，过于理想化的假设从理论上限制了其在强非均质性页岩中的应用。

近年来，基于吸附势理论的微孔充填模型在页岩气及煤层气等温吸附研究中得到越来越广泛的应用[27-33]，其具有清晰的物理背景，结合虚拟饱和蒸气压可用于超临界气体在固体表面的吸附表征[34]。早前，研究者们采用微孔充填吸附模型时直接利用实验数据进行拟合，以拟合精度评价模型适用性。熊健等[31]研究发现，同一样品在不同温度下通过上述处理方式得到的吸附特征曲线并不唯一，这与吸附势理论基本假设相悖。为此，熊健等将吸附特征曲线和吸附模型相结合提出改进算法。然而，上述研究中等温吸附实验压力均不超过15 MPa，并且过剩吸附量数据均未出现下降段。由于地层压力随深度递增，深层页岩储层压力远超中浅层页岩储层[35]，上述文献中方法对深层高压页岩中甲烷吸附数据适用性情况不明，亟待开展相应的研究工作。此外，部分研究者在选取吸附相密度时或将其视为定值，或将其视为温度的函数，未考虑样品的差异对吸附相密度的影响。

为此笔者在前人研究的基础上，基于广泛使用的微孔充填Dubinin-Astakhov吸附模型，结合不同温度下的超临界甲烷吸附实验数据，研究了高压（大于等于20 MPa）下甲烷在页岩中的吸附特征，探讨了常用吸附相密度计算方法在高压吸附下的适用性，基于循环迭代和最优化思路提出了结合吸附特征曲线优化高压下Dubinin-Astakhov吸附模型参数的新方法，以期为深层高压页岩气藏储量评估和开发方案制定提供依据。

1 超临界Dubinin-Astakhov吸附模型

根据吸附势理论，页岩样品中吸附势与吸附相体积的关系曲线是唯一的，该曲线称为吸附特征曲线[17,29,31]。研究表明，甲烷在页岩中的等量吸附热小于40 kJ/mol，属于典型的物理吸附[24,36-40]。对于物理吸附，其吸附作用力主要为色散力，而色散力与温度无关，使得吸附特征曲线不受环境温度影响[31]。因此，吸附特征曲线唯一性是基于吸附势理论推导的微孔充填吸附模型所必须遵循的基本准则。

吸附势理论认为，孔壁对气体存在吸附势场，并且吸附势大小与孔径相关，孔径越小其曲率越大，吸附势发生重叠导致孔壁对气体分子吸附作用也更强[17]。吸附势表示1 mol气体分子被孔道壁面吸附过程中发生的自由能变化，根据Polanyi[41]吸附势理论，其计算式为：

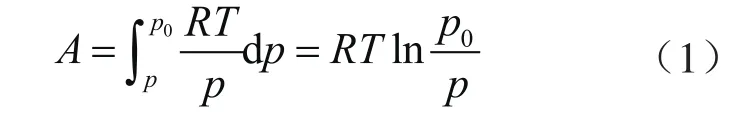
式中A表示吸附势，J/mol；R表示通用气体常数，取值8.314 J/(mol K)；T表示吸附测试温度，K；p0表示饱和蒸气压，MPa；p表示吸附平衡压力，MPa。

甲烷临界温度Tc为－82.6 ℃，因此不论是在室内等温吸附实验环境还是储层条件下甲烷均处于超临界状态，而超临界气体一大特性是无法液化。在吸附势的求取中，饱和蒸气压计算至关重要，显然对于甲烷在页岩中的吸附而言饱和蒸气压是没有物理意义的。为此，研究者们提出了虚拟饱和蒸气压概念。1960年，Dubinin[42]提出了著名的虚拟饱和蒸气压，其计算式为：

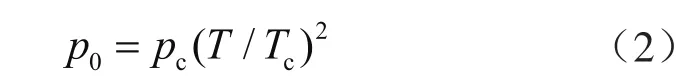
式中pc表示临界压力，对于甲烷气体取值4.599 2 MPa。

上述虚拟饱和蒸气压计算式在气—固吸附中得到广泛应用，但与此同时研究者们也发现了其不足：公式忽略了吸附体系的差异，导致模型拟合效果不够理想[33]。随后，Amankwah等[43]于1995年提出了改进计算，即

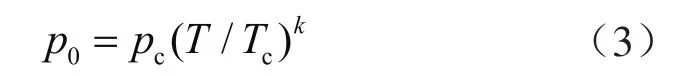
式中k值是与吸附体系相关的参数。

k值的引入使得虚拟饱和蒸气压计算式能够反映出不同吸附体系的差异，并获得了不错的效果[33]。此外，Reich等[44]、Sakurovs等[45]也提出了虚拟饱和蒸气压计算式。

在吸附特征曲线中另一个重要参数是吸附相体积，根据甲烷在页岩中真实吸附气含量及吸附相密度可获得吸附相体积如下：

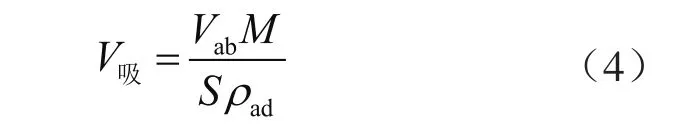
式中V吸表示微孔中吸附相体积，cm3/g；Vab表示甲烷在页岩中真实吸附气含量对应的地面标况下气体体积，cm3/g；S表示地面标况下单位摩尔气体体积，取值22 400 cm3/mol；M表示甲烷气体摩尔分子质量，取值16.042 8 g/mol；ρad表示吸附相甲烷密度，g/cm3。

根据吸附势理论，Dubinin和Astakhov于1971年提出了著名的Dubinin-Astakhov吸附模型，其计算式为[31,46]：

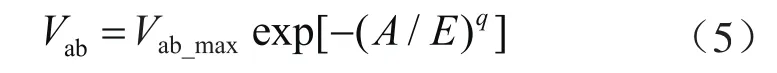
式中Vab_max表示页岩最大吸附气含量对应的地面标况下气体体积，cm3/g；E表示吸附特征能，与温度无关，只随吸附体系变化而变化，J/mol；q表示与吸附剂表面非均匀性相关的常数，只由吸附剂决定。

当q=2时，上述表达式退化为Dubinin-Radushkevich吸附模型。显然，增加参数q会使得模型具备更好的适应性。

联立式（4）、（5）可推得：

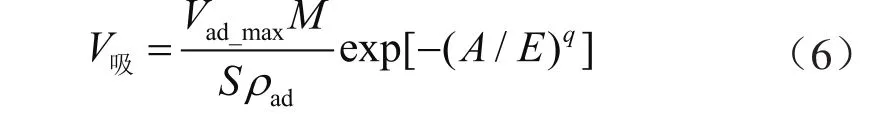
可知，式（6）等价于：

式中V微孔表示微孔充填最大吸附气含量时对应的吸附相甲烷体积，cm3/g。对于给定的页岩样品，q为定值，吸附特征能（E）由吸附体系决定并为定值。根据吸附势理论，吸附相体积（V吸）和吸附势（A）在同一关系曲线上，由式（7）不难看出V微孔应为与温度无关的定值。值得注意的是，这里的V微孔并不等同于页岩微孔体积。

联立式（1）、（4）、（7）可得 ：

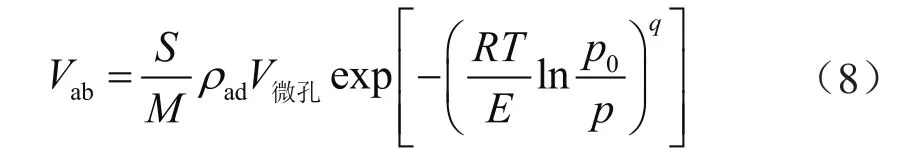
上述关系式（8）可称之为Dubinin-Astakhov吸附模型的变形式，其实质还是Dubinin-Astakhov吸附模型。结合式（7）可知，采用式（8）变形后的Dubinin-Astakhov吸附模型对同一样品在不同温度下的吸附数据进行拟合时，必须保证拟合参数V微孔、E和q是相同的，否则无法满足吸附特征曲线的唯一性。

2 超临界等温吸附实验数据

本文实验数据来自前人研究成果[19,25]，所选用页岩样品均来自四川盆地志留系龙马溪组，分别记为样品1和样品2。样品1取样深度为2 400.8 m，TOC含量为4.52%，Ro介于2.2%～2.5%；样品2取样深度介于3 174.49～3 177.41 m，TOC含量为3.71%，Ro为2.4%。

样品1等温吸附实验采用重量法开展，所用仪器为德国Rubotherm高温高压吸附仪，分别在30 ℃、45 ℃、60 ℃和80 ℃条件下进行吸附测试，所得实验数据最高压力为27 MPa。样品2等温吸附实验采用容积法开展，所用仪器为美国Core Lab公司的GAI-100型油浴高温高压吸附仪，分别在40.6 ℃、60.6 ℃、75.6 ℃和95.6 ℃条件下进行吸附测试，所得实验数据最高压力超过50 MPa。两块页岩样品所获实测过剩吸附量数据如图1所示。

图1可知，随着压力增加样品1、2的过剩吸附量均先增加后下降，出现了极大值，这与其他文献中报道的高压下甲烷在页岩中的吸附现象是一致的[18,20-24,26]。当温度为30 ℃时，样品1在压力为8 MPa附近时出现过剩吸附量极大值，而温度为80 ℃时出现过剩吸附量极大值时的压力约为12 MPa。在温度为40.6 ℃时，样品2在压力为13 MPa附近时出现过剩吸附量极大值，而温度为95.6 ℃时出现过剩吸附量极大值时的压力约为19 MPa。此外，样品1、2在60 ℃左右时出现过剩吸附量极大值的压力约为12 MPa和17 MPa，存在较大差异。总的来看，随着温度的增加过剩吸附量极大值随之减小，过剩吸附量极大值对应拐点压力随之增加，并且不同样品间出现过剩吸附量极大值的压力点存在差异。

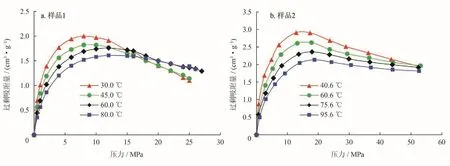
图 1 页岩样品实测过剩吸附量数据分布图

3 实验结果处理及探讨

3.1 过剩吸附量和绝对吸附量的转换

如前所述，实验直接测得的吸附气含量为过剩吸附量，该测试结果不能反映页岩样品的真实吸附能力，究其原因在于其忽略了吸附相体积的影响，从而低估了页岩吸附甲烷的能力。过剩吸附量和绝对吸附量满足如下关系[13]：

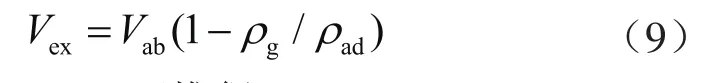
联立式（4）、（9）可推得：

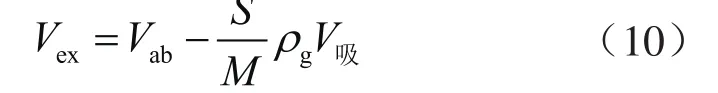
式中Vex表示过剩吸附量，即实验直接测得的吸附气含量对应的地面标况下气体体积，cm3/g；ρg表示自由相甲烷密度，g/cm3。

绝对吸附量（Vab）、吸附相体积（V吸）以及自由相甲烷密度（ρg）均随压力增加而增加，当压力较低时自由相甲烷密度较低，此时相同压差下绝对吸附量的增量高于(S/M)ρgV吸项的增量，过剩吸附量表现为随压力增加而增加；当压力增加到一定程度后，绝对吸附量和吸附相体积增速放缓，但自由相甲烷密度仍然保持较大增速，因此测得的过剩吸附量会出现极大值。早期等温吸附研究中，很多实验未出现过剩吸附量极大值，主要原因是实验压力过低，或所选吸附剂为煤、活性炭等具有较强吸附能力的物质，这些物质出现过剩吸附量极大值的压力会相应的后延。结合式（8）、（9），可推导过剩吸附量表达式为：

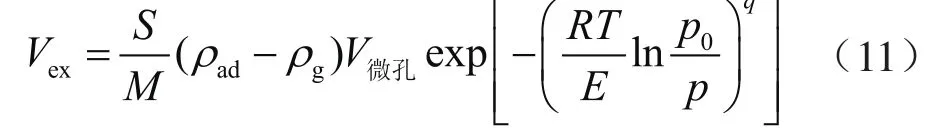
值得注意的是，从推导过程来看上述表达式仍然是基于Dubinin-Astakhov吸附模型的变形式。

3.2 吸附相和自由相甲烷密度的选取

目前，学者们基于式（9）开展过剩吸附量的校正工作，因此自由相甲烷密度和吸附相甲烷密度的准确性及合理性至关重要。本文通过美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）化学数据库直接查询获取任意给定温度压力下的自由相甲烷密度[47]。文献中关于吸附相甲烷密度的确定方法较多，大体可归纳为4类，如表1所示。

表1 不同吸附相甲烷密度取值方法总结表

为了对比分析上述吸附相甲烷密度计算方法在高温高压条件下的适用性，采用式（9）对实测等温吸附实验数据进行过剩吸附量校正。如图2-a、b所示，对于样品1，当吸附相甲烷密度取值为0.373 g/cm3、0.425 g/cm3时，明显可见在温度为30 ℃、45℃时校正得到的绝对吸附量在压力超过15 MPa后随压力增加反而下降，周尚文等[18]在研究中也发现类似现象。虽图2-e、f中样品2所获得的校正绝对吸附量趋势较好，但上述结果仍可说明Arri等[48]和Yee等[49]提出的吸附相甲烷密度取值方法在高压下并不一定适用。

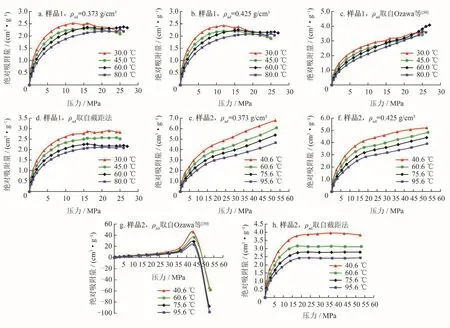
图2 不同方法校正后所得绝对吸附量图

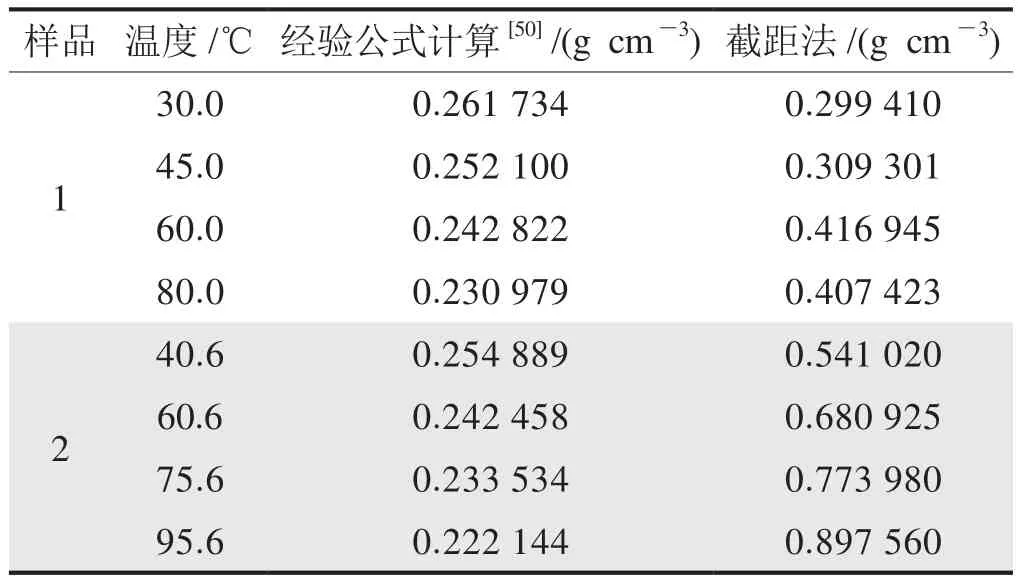
表2 不同方法下吸附相甲烷密度取值表

图3是针对两个页岩样品在高压下做出的过剩吸附量与自由相甲烷密度关系图，基于截距法可利用拟合直线关系式计算出样品1、2在不同温度下的吸附相甲烷密度，计算结果见表2。研究认为，吸附相甲烷密度合理取值介于0.162～0.425 g/cm3。图2-d、h可知，采用截距法计算的吸附相甲烷密度对过剩吸附量数据校正后能够获得不错的结果，但很明显对于样品2采用该方法计算所得吸附相甲烷密度过高（表2），并且在高压段该方法校正的绝对吸附量表现出饱和吸附特征，即吸附气含量随压力变化不大，但在该压力范围内样品是否一定达到饱和吸附状态尚未有定论。综上分析，截距法的适用性和正确性也存疑。

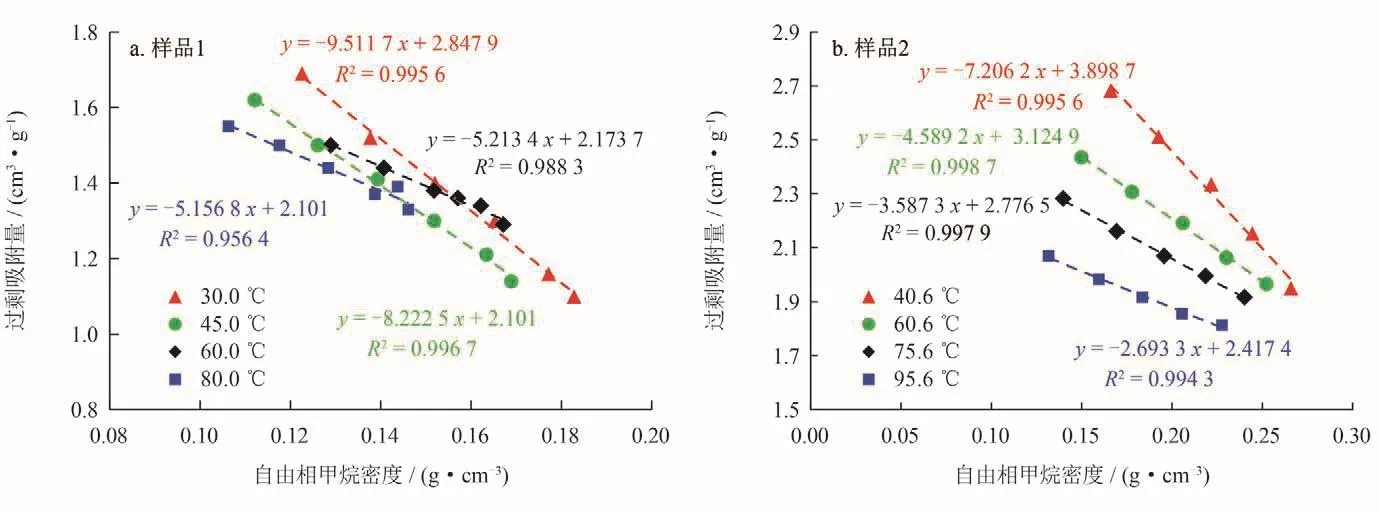
图3 高压下过剩吸附量与自由相甲烷密度关系图

进一步将吸附相甲烷密度视为待拟合参数，采用Dubinin-Astakhov吸附模型拟合实验数据。为体现吸附体系差异，本文采用Amankwah等[43]提出的虚拟饱和蒸气压计算式，式（11）可变换为：

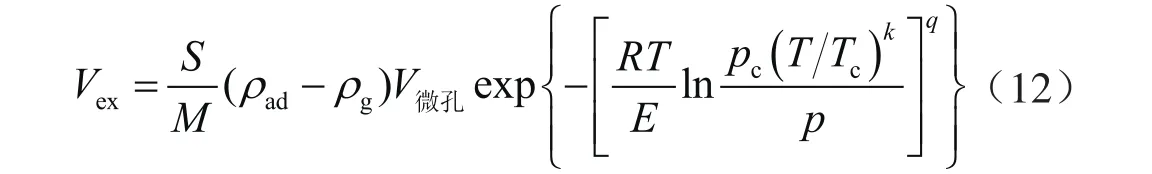
通常，学者们直接采用等温吸附模型对实验数据进行拟合，并以拟合系数（R2）作为拟合效果好坏的评判标准。采用式（12）对样品1、2在不同温度下的实测过剩吸附量数据拟合，拟合模型参数见表3。样品1模型R2在0.99以上，样品2的模型R2在0.98以上（表3），从拟合效果来看Dubinin-Astakhov吸附模型的适用性较好。

在不同温度下，采用表3中拟合模型参数计算得到吸附相体积和吸附势并在笛卡尔坐标系中描点作图（图4）。虽然模型拟合过剩吸附量与实测过剩吸附量吻合程度很高，但不同温度下的吸附特征曲线并不统一。由表3知，不同温度下模型拟合参数V微孔、E和q不一致，由式（7）可知，此时的吸附特征曲线必然不唯一。因此，如果直接采用Dubinin-Astakhov吸附模型对不同温度下的实验数据进行拟合，虽然能保证得到最佳的拟合效果，但是其结果实际上是违背吸附势理论的。此外，当温度为95.6 ℃时样品2拟合获得的吸附相密度超过了其上限值0.425 g/cm3。

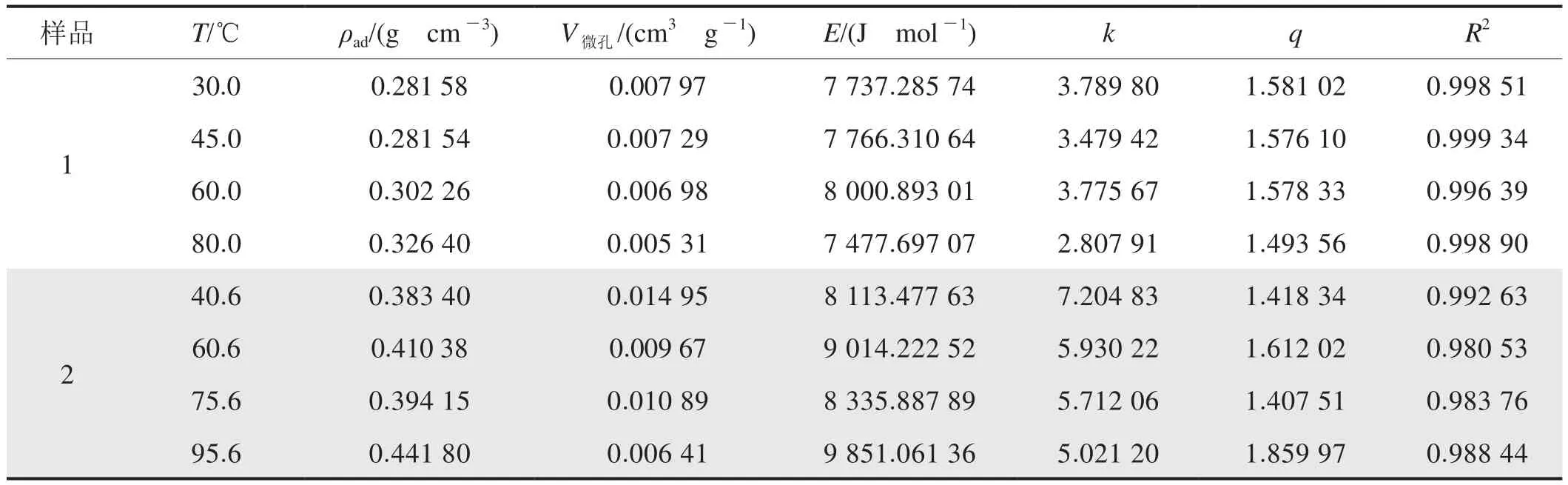
表3 直接采用Dubinin-Astakhov吸附模型拟合获得参数表

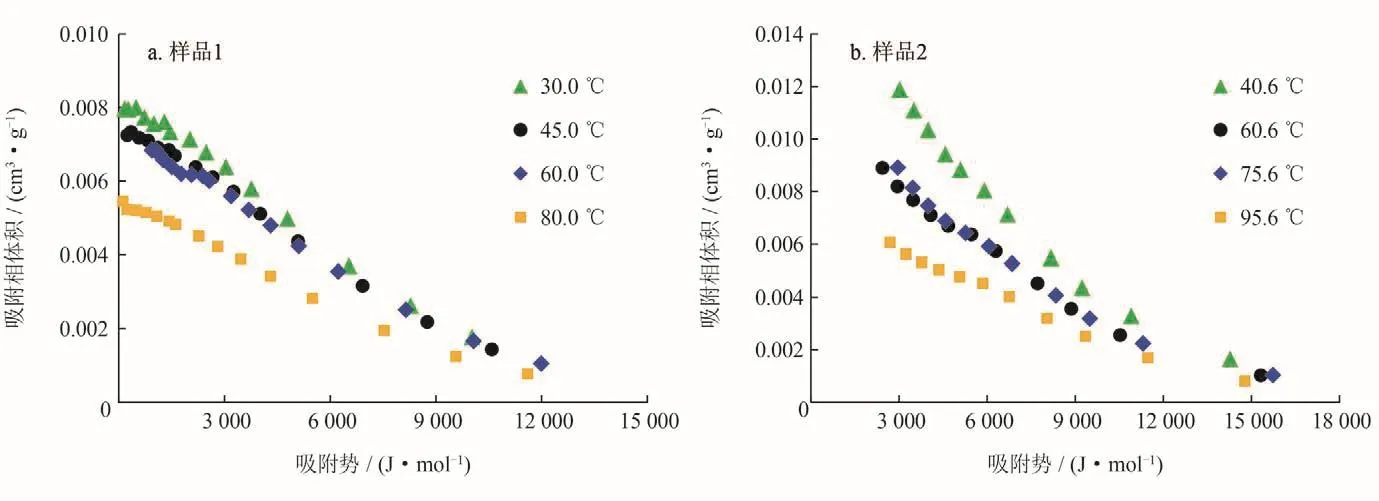
图4 直接采用Dubinin-Astakhov吸附模型拟合获得吸附特征曲线图

3.3 Dubinin-Astakhov模型参数优化新方法

采用Amankwah等[43]提出的虚拟饱和蒸气压计算式时，由式（7）可知吸附相体积表示为：

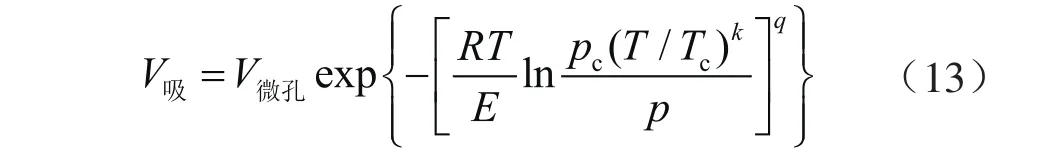
此外，联立式（4）、（9）可知：

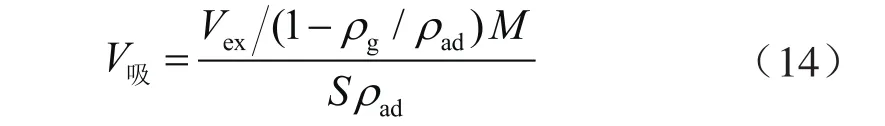
当吸附相甲烷密度为定值时，式（14）计算的吸附相体积也是定值。通过调整式（13）中的k值可以使得吸附势改变，此时可以将不同温度下吸附势和吸附相体积的关系曲线往同一位置调整，以满足吸附特征曲线的唯一性。学者们采用上述方法取得了不错的效果，但是在他们的实施方案中，采用的是经验公式计算吸附相甲烷密度，并且所用实验数据压力均未超过15 MPa[29,31]。此外，前人在求取最佳k值时是通过求取一系列离散k值下的吸附特征曲线拟合系数（R2），进而找到最大R2对应的k值为最优k值，这样的求取方式不仅费时费力且精度没有保障。

实际上，对于同一页岩样品而言，V微孔、E、k和q应该是统一的[31]，因此可以直接采用公式（13）对不同温度下计算出的所有吸附相体积数据进行拟合，从而获得最优的模型参数。采用表3中直接拟合Dubinin-Astakhov吸附模型获得的不同温度下吸附相甲烷密度，结合式（14）计算出不同温度和压力下页岩样品中的吸附相体积，然后采用式（13）对同一页岩样品的所有吸附相体积数据进行拟合获得统一的模型参数，拟合结果如图5、6。为与后文内容衔接，称此处理为一次优化。由图6可知通过统一调整模型参数V微孔、E、k和q，样品1、2在不同温度下的吸附相体积和吸附势关系曲线更加趋于重合，较图4有了显著的提升。需要注意的是，虽然吸附特征曲线得到改善，但由图5可知采用统一的模型参数后在高压段计算出的过剩吸附量与实测过剩吸附量存在较大偏差。因此，直接采用上述优化处理方式会牺牲高压段过剩吸附量计算精度，导致得到的绝对吸附量不准确。

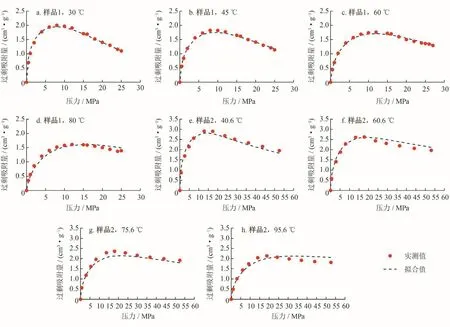
图5 采用一次优化后模型参数计算的过剩吸附量与实测过剩吸附量对比图

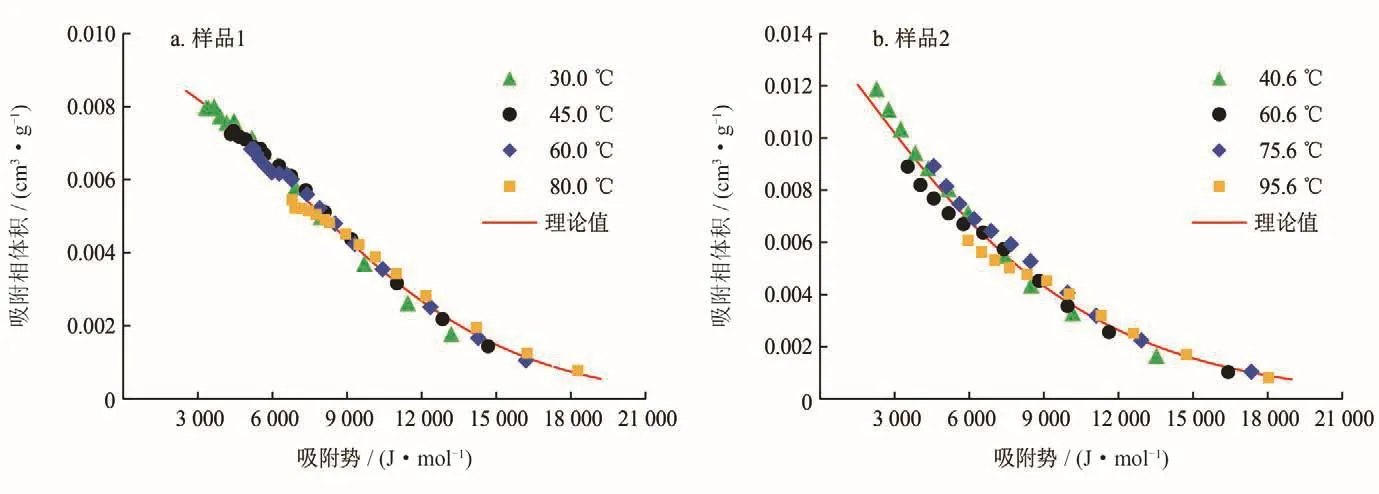
图6 采用一次优化后模型参数计算的吸附特征曲线图

实际上，上述吸附相甲烷密度是通过拟合获得的，进一步调整吸附相甲烷密度可以使得计算出的过剩吸附量与实测过剩吸附量吻合程度更高。受此启发，本文基于循环迭代和最优化思路提出优化Dubinin-Astakhov吸附模型参数并计算页岩中绝对吸附量的新方法，具体步骤如下：

大部分物流企业在成本核算时不能对所有的费用进行归集。对有些物流人员消极怠工或者工作效率低而增加时间成本也没有重视起来。

1）分别在不同温度下利用式（12）变形的Dubinin-Astakhov吸附模型拟合实验测得的过剩吸附量数据，获得不同温度下的吸附相甲烷密度（ρad）、样品微孔体积（V微孔）、吸附特征能（E）以及参数k和q，利用式（14）计算出不同温度、压力测点下的吸附相体积（V吸），记参数优化次数n = 0。

2）采用式（13）对获得的所有不同温度、压力下的吸附相体积数据进行拟合，在拟合R2最大时获得统一的样品微孔体积（V微孔）、吸附特征能（E）以及参数k和q，并记此时的拟合系数（R2）为Rmax，记参数优化次数为n = n + 1。

3）分别在不同温度下，将步骤2）中获得的统一样品微孔体积（V微孔）、吸附特征能（E）以及参数k和q带入式（12）变形的Dubinin-Astakhov吸附模型，利用实测过剩吸附量数据获得不同温度下模型拟合系数（R2）最大时的吸附相甲烷密度（ρad），并利用式（14）更新计算不同温度、压力测点下的吸附相体积（V吸）。

4）循环重复步骤2）、3），直到相邻两次Rmax变化在0.001%以内，此时步骤2）中获得的样品微孔体积（V微孔）、吸附特征能（E）以及参数k和q即为模型最优参数，步骤3）获得不同温度下页岩样品中最优吸附相甲烷密度值。

5）将上述步骤中获得的最优吸附模型参数和吸附相甲烷密度带入式（8）计算页岩样品中绝对吸附量。

采用上述新方法对样品1、2的实测过剩吸附量数据进行模型优化求解，直至达到收敛，并计算出新方法实施步骤2）中吸附相体积关系式[公式（13）]拟合Rmax随优化次数变化结果。对样品1的实测过剩吸附量数据进行一次优化拟合时Rmax为0.974 49，经过24次循环迭代优化后达到收敛，拟合Rmax上升至0.995 79，提升2.13个百分点；对样品2的实测过剩吸附量数据进行一次优化时Rmax为0.940 13，经过12次循环迭代优化后达到收敛，拟合Rmax上升至0.983 34，提升4.32个百分点。定义样品1、2在不同温度下预测的过剩吸附量与实测过剩吸附量之间的吻合系数（β）：

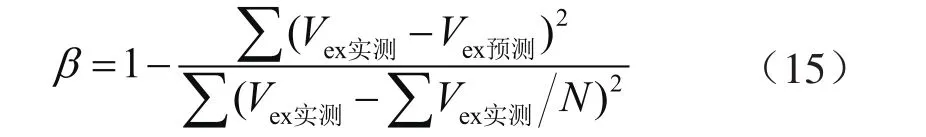
式中N表示等温吸附实验测试点数。

β越接近1，说明预测的过剩吸附量越准确。随着迭代优化的次数增加，整体上β逐渐增加并最终达到稳定（图7）。

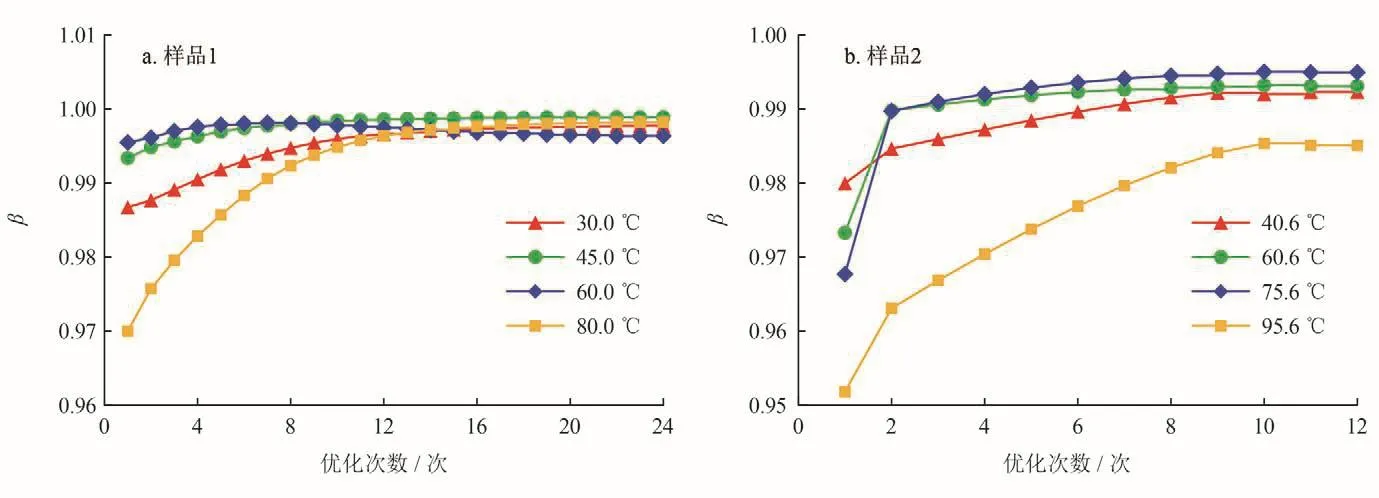
图7 不同样品预测过剩吸附量吻合系数与优化次数关系图

表4中给出了样品1、2在不同温度下的优化拟合参数，可以看到经过迭代优化后两个样品在不同温度下得到的吸附相甲烷密度都非常接近，样品1得到的吸附相甲烷密度均值为0.290 285 g/cm3，样品2得到的吸附相甲烷密度均值为0.399 078 g/cm3。为说明同一样品在不同温度下计算得到的吸附相甲烷密度之间离散程度，定义均值偏差，其计算式为：

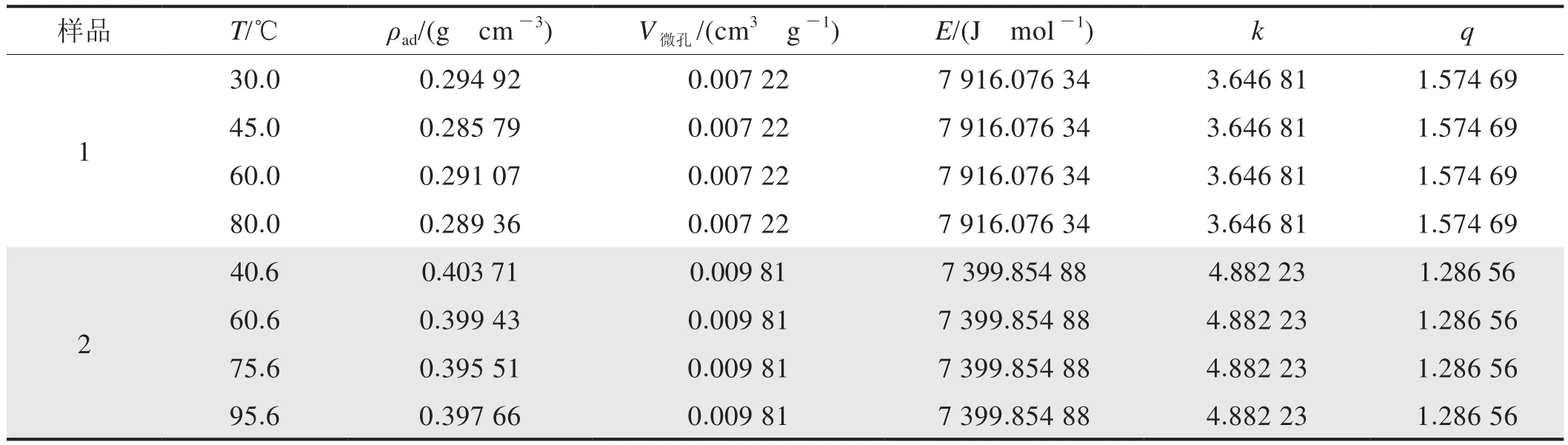
表4 优化收敛后获得模型参数表

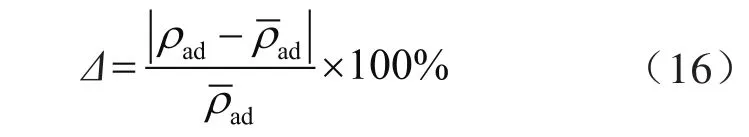
计算出两个样品在不同温度下的吸附相甲烷密度均值偏差，分析发现虽然同一样品在不同温度下获得的吸附相甲烷密度在数值上有微小差异，但是均值偏差非常小，均不超过1.6%，说明同一样品在不同温度下的吸附相甲烷密度值离散程度极低。考虑实验数据存在合理微小误差，上述结果表明温度对给定页岩样品中吸附相甲烷密度影响很小。此外，可以看到不同样品中获得的吸附相甲烷密度存在明显差异，由于文中所用两块页岩样品来自不同取心井及地层深度，其地化参数也存在显著差异，这表明吸附相甲烷密度与页岩样品自身属性密切相关，这可能与不同样品中甲烷分子受到孔隙壁面的吸附力有关。

采用优化后模型参数计算作图（图8），预测的过剩吸附量与实测过剩吸附量吻合度高，相比于一次优化时（图5）有了显著改善。图9可知，采用新方法进行循环迭代优化后，样品1、2在不同温度下的吸附特征曲线均更加趋于统一。

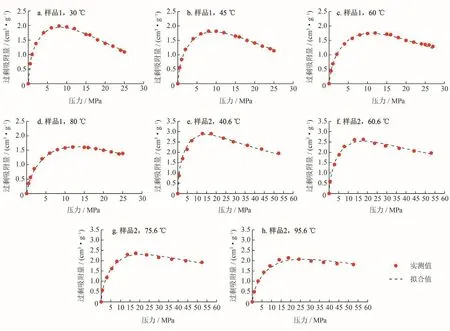
图8 优化收敛后过剩吸附量与实测过剩吸附量对比图

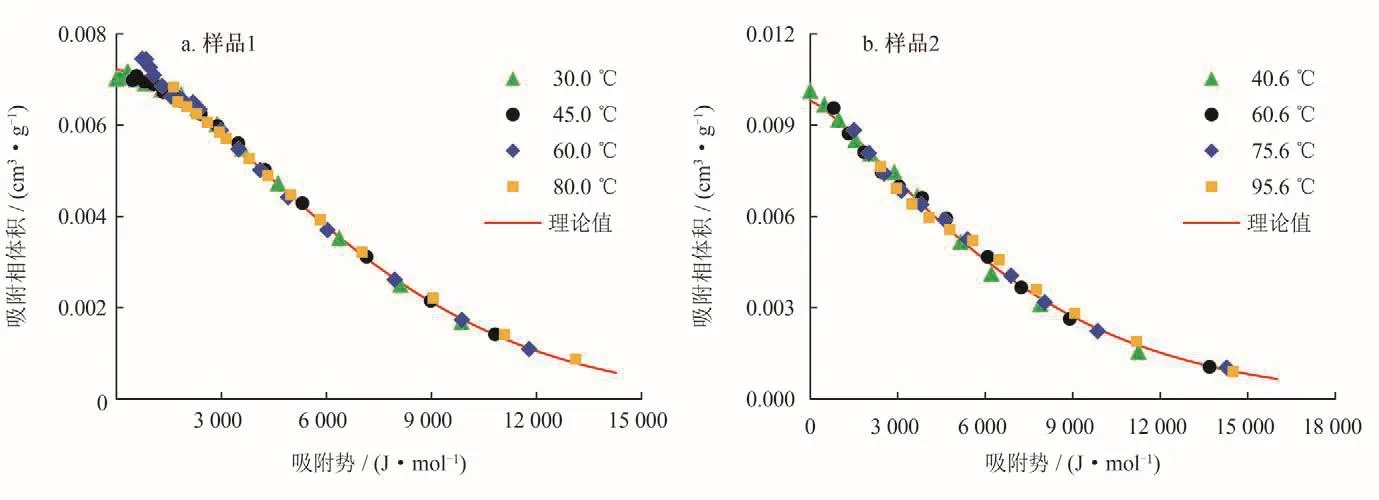
图9 优化收敛后模型参数计算的吸附特征曲线图

当采用Amankwah等[43]提出的虚拟饱和蒸气压计算式时，其表达示为：

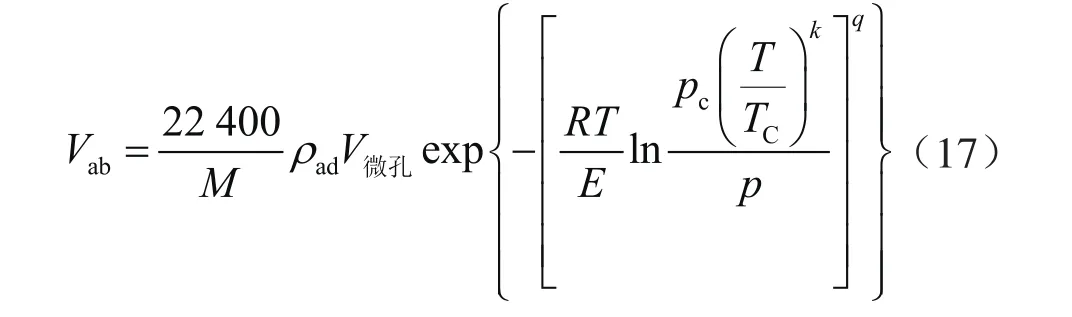
将优化收敛后获得的模型参数带入上式可计算出不同温度下甲烷的绝对吸附量，如图10所示。

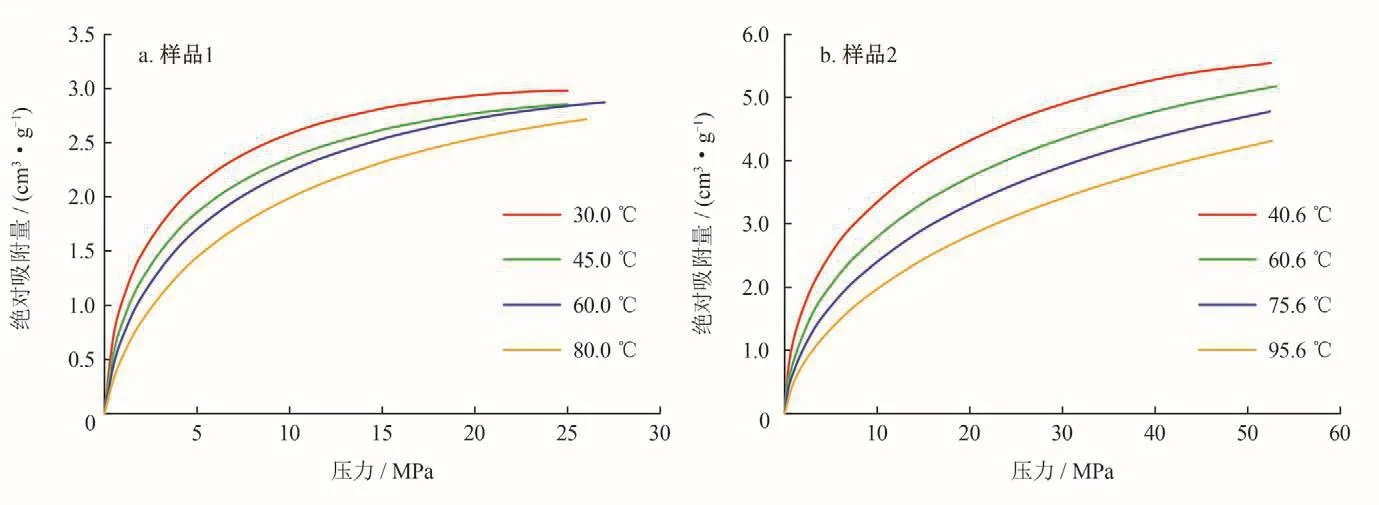
图10 Dubinin-Astakhov模型参数优化页岩中甲烷绝对吸附量图

4 结论

1）采用定值吸附相甲烷密度（如0.373 g/cm3、0.425 g/cm3）、经验公式或截距法求取吸附相甲烷密度的过剩吸附量校正方法对于计算高压条件下甲烷在页岩中的绝对吸附量并不适用，主要误差出现在高压段。

2）采用Dubinin-Astakhov吸附模型开展不同温度实测过剩吸附量数据拟合，既要保证不同温度下的过剩吸附量数据拟合准确，又要兼顾吸附特征曲线的唯一性；仅仅对单一温度下的吸附数据进行拟合时，获得的结果准确性没有保证。

3）温度对给定页岩样品中的吸附相甲烷密度影响很小，且吸附相甲烷密度与吸附体系相关，不同井区和层位页岩中吸附相甲烷密度可能存在较大差异，不能一概而论。

4）提出对Dubinin-Astakhov模型参数优化的新方法，使得计算结果满足吸附势理论，并可获得唯一的吸附特征曲线，使计算出的过剩吸附量与实测过剩吸附量具有很好的一致性，可为深层高压页岩气藏储量评估提供理论依据，支撑深层页岩气藏经济高效开发。