受干扰机器人网络控制系统事件驱动控制研究
陈帝翰,刘 霞
(西华大学电气与电子信息学院,四川 成都 610039)
网络控制系统(networked control system)是由传感器、控制器和执行器等组成的闭环系统,各组件通过网络相互连接,与传统的现场总线型控制系统相比,拥有安装简单、维护方便、兼容性高等优越性,已广泛应用于多个领域,如车辆、飞机和航天器等[1-2]。但网络中往往存在时延、丢包、数据包乱序、网络阻塞等影响,这不可避免会降低系统的控制性能,甚至破坏其稳定性[3-5]。
近年来,一些学者针对网络控制系统的时延、丢包等问题进行了大量研究[6-10]。文献[6]将网络中的时延分为前馈时延和反馈时延2 部分,采用滑模预测控制方法对一类线性系统进行控制;但是由于其控制器采用时间驱动的模式工作,若频率过大,频繁的控制动作会导致抖振的加剧,而频率过小又无法达到有效的控制。文献[7]讨论了一类非线性网络系统的稳定性问题,考虑网络的时变、时延,将闭环网络控制系统重构为具有多个开关信号的线性切换系统,设计了一种基于切换系统理论的合成控制方法,将复杂的非线性系统问题分解为多个线性子系统的问题,但是实际中很难实现这样的分解。文献[8]针对一类线性连续系统的时变、时延问题,提出了一种结合模式相关状态反馈控制器的切换系统方法,这种模式相关控制器根据不同的时延切换不同的控制增益;但是实际中准确的时延是很难估计的,如果时延的估计不准确将会导致控制器的增益调节效果不理想,最终影响系统的控制性能。文献[9]将线性的Hammerstein 模型作为研究对象,考虑网络诱导时延,结合状态观测器设计了一种基于实时预测的补偿策略,通过实时的状态信息来计算最优控制序列。上述网络控制系统多采用时间驱动的方式,即:通过时间戳来保证系统时钟统一,系统中各部件按照固定的周期动作。对于这类时间驱动的网络控制系统,当出现时延估计不准确或丢包率过大的情况时,可能会导致系统不稳定,大大降低系统的控制性能。
为了避免时间驱动网络控制系统存在的上述问题,学者们提出了事件驱动的控制方法[10~11]。事件驱动控制方法的目标仅聚焦于被控对象的期望目标是否达成,而不是控制量作用于被控对象上的时间。即事件驱动只要控制目标没有达到,就继续操作,而不会像时间驱动一样定时操作,因而大大降低了时延对系统的影响。文献[11]针对一类线性多智能体系统的一致性问题,结合状态观测器设计了一种采用事件驱动机制的输出反馈控制器。文献[12]针对非线性网络控制系统,设计了一种基于数据的事件驱动控制方法,降低了系统中时延对控制性能的影响。但是在实际情况中,网络控制系统除了存在时延外,往往还存在外部干扰的影响[13-17]。文献[13]考虑网络控制系统的时变、时延,提出了一种基于通信干扰观测器的二阶线性过程时延补偿控制结构,并且设计了降阶干扰观测器和干扰补偿器来处理外部干扰。文献[14]针对一类受外部干扰影响的线性系统,提出了一种事件驱动的触发机制,该触发机制需要获取系统状态信息,在实际中实现较困难。文献[15]针对一类具有外部扰动的不确定连续系统,考虑系统运行中存在网络阻塞问题,提出了一种基于模型的自适应事件驱动控制方法,使系统能够在控制网络中在线调节状态。文献[16]针对一类具有随机扰动的非线性系统,考虑信息传输过程中存在数据包丢失,提出了一种模型预测控制方法来补偿传输信道中丢包对系统稳定性的影响。然而,文献[15—16]对于模型精确度的要求较高,在实际中很多时候无法获取精确的系统模型。文献[17]针对一类具有外部干扰的非线性系统,考虑网络诱导时延,提出了一种基于增广状态观测器的网络化预测量化控制方法,采用2 个任意区域量化器对信号进行合理取值,但是该量化器只是减少了数据包的大小,而没有减少数据包的数量,对于信息传输的优化效果有限。
本文针对非线性机器人网络控制系统受到的外部干扰,同时考虑网络本身存在的随机时延,结合干扰观测器设计了一种事件驱动控制方法:控制器在判定被控机器人的输出误差是否满足预设事件的同时,接收来自干扰观测器的干扰观测值,当控制器判定系统输出误差不满足预设事件时,控制器利用系统输出误差和干扰观测值计算出新的控制输入来替换原来的控制输入信号,否则控制器保持上一时刻的控制输入。这样既减少了控制器的无效动作,也使整个系统更加稳定。
1 问题描述
网络控制器(Netcon)是网络控制系统的核心。本文将网络控制器分为远端网络控制器和本地端网络控制器。对于受外部干扰影响的非线性机器人网络控制系统,其系统由远端网络控制器、PC 端、本地端网络控制器、被控机器人和干扰观测器组成,如图1 所示。其中远端网络控制器与PC 端进行有线连接,本地端网络控制器与被控机器人、干扰观测器进行有线连接,远端网络控制器与本地端网络控制器通过网络连接。当系统运行时,本地端网络控制器在接收到来自远端网络控制器的理想控制信号(t)的同时,利用来自干扰观测器的干扰观测值(t)计算出实际控制输入 τ(t),并发送给被控机器人。其中Y(t)为机器人输出序列,d(t)为外部干扰。

图1 受干扰机器人网络控制系统
实际网络往往存在时延与丢包等影响。本文假设网络随机时延为ξ,系统最大连续丢包数ζl已知。
令n关节机器人数学模型为
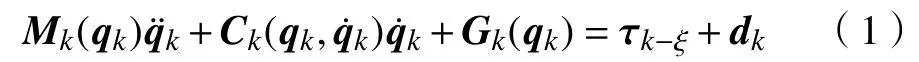
假设1网络中随机时延ξ的上限不大于采样周期T的 ρk倍(ρk为正整数),即≤ρkT。例如,假设k时刻的网络时延为0.2 s,采样周期T为0.02 s,则ρk的值为10。
假设2系统的最大连续丢包数 ζl小于采样周期的倍数,即ζl<ρk。例如,假设k时刻 ρk的值为10,则ζl<10。
2 干扰观测器的设计
在实际的机器人网络控制系统中,外部干扰的影响不可避免,且无法直接获取准确的干扰值。本文针对这一问题,设计了一种周期性的干扰观测器来观测系统受到的外部干扰,并在每一个采样时刻将干扰观测值发送给控制器。
针对机器人模型式(1),得

现设计干扰观测器,为
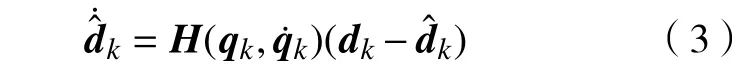
式中:H(qk,)为k时刻干扰观测器正定增益矩阵,记为Hk;为k时刻的干扰估计值。
将式(2)代入式(3),得

假设干扰的变化是缓慢的[18],即

定义k时刻的观测误差 σk,为

由式(3)、(5)和(6)可以得到观测误差函数,为

再定义辅助向量zk,为

通过设计辅助矩阵Ak使得观测器稳定。
增益矩阵Hk=diag{c,c}由方程式(9)给出,其中常数c>0。

则干扰观测器为

接下来设计Ak。
双关节机器人的正定惯性矩阵由式(11)给出。

式中:m1,m2为关节连杆质量;l1,l2为关节的连杆长度;r1,r2为连杆关节点和连杆质心的距离;qk(1)为k时刻机器人关节1 位置;qk(2)为k时刻机器人关节2 位置;g为重力加速度;i1,i2是与m1,m2,l1,l2,r1,r2有关的机器人系统参数。
定理 1对于机器人式(1),设计观测器式(10)中的Ak,为

且满足

则观测器式(10)全局渐近稳定。其中:qmax(2)为关节2 的最大位置;(2)为关节2 的最大角速度。
证明由式(12)知

根据式(12)与式(9),可得
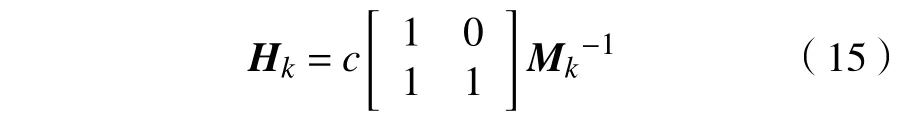
由于Mk正定,则有

代入式(15),得

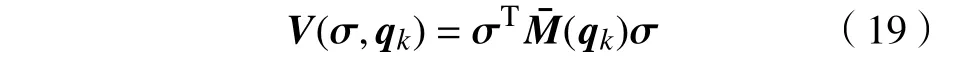
对式(19)求导,并将误差函数式(7)代入,可得

根据式(13)中常数c的定义,有2c>0且有

3 事件驱动控制的设计
一般的时间驱动控制系统在一定的时间间隔时会定时对被控对象进行控制输入,于是往往会发生很多不必要的控制动作,迫使系统对网络的通信信道带宽要求较高,成本也相对较高。例如:当系统中的控制效果已经达到期望时,控制器依然不断地输入控制量,会造成不必要的网络信道带宽的浪费;当系统中出现来自外部或自身的干扰时,系统的控制能力会受到影响,在这种情况下,可能这些不必要的控制动作会使控制效果降低,甚至使系统不稳定。为了减少系统中不必要的控制动作,本文设计了一种事件驱动控制方法,在考虑随机时延的同时,对干扰进行补偿。机器人网络控制事件驱动控制方法是只有当系统误差满足条件时进行控制动作,从而避免了传统控制方法的无效动作,以节约网络带宽。机器人网络控制事件驱动系统运行步骤如下。
1)在k-ξ时刻,本地端网络控制器接收到机器人的输出Yk-ξ后,通过计算机器人关节误差,与预设的最大允许误差 ε比较。设定预设事件Ψ,当本地端控制器判定机器人的位置跟踪误差ek-ξ不满足预设事件Ψ 时,向远端控制器发送触发信号。
2)假设在k时刻远端网络控制器接收到触发信号,计算出k+ξ时刻的理想控制输入,并发送给本地端网络控制器。
3)本地端网络控制器在k+ξ时刻接收到理想控制输入量的同时,利用干扰估计值计算出补偿干扰后最终的控制输入τk+ξ并发送给被控机器人。
在上述整个过程中,干扰观测器将一直处于工作状态。下面进行控制律的设计。
(2)改写为

式中:φk表示k时刻的矩阵φ(Xk);Xk(i)表示k时刻X的第i个元素;μ为常数并满足0<μ<1。
将式(21)改写为

令被控机器人期望输出序列为Yd,k时刻输出误差为ek,有
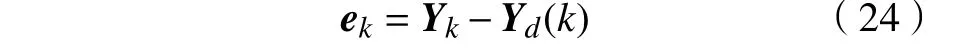
式中Yd(k)为被控机器人期望输出序列Yd的第k个值,表示被控机器人k时刻的期望输出值。
构造被控机器人关节误差函数,为

其中τd(k)为k时刻与期望输出序列对应的期望输入序列。
预先设计事件条件Ψ,为

本文假设采样间隔为T,在每一个采样时刻γT,本地端控制器将确认事件条件Ψ 是否满足,若不满足事件条件 Ψ,则触发控制动作。其中γ ∈Z+。
设计事件触发机制,为

式中kβ+1表示第β+1次触发控制器动作的时刻。
将式(25)改写为

其中T∈Z+,0 ≤l≤T-1,γ=0,1,2,···,n。采样时刻间隔示意如图2 所示,其中γT+l+1表示非采样的一般时刻。

图2 采样时刻间隔
利用式(10)得到k时刻的干扰估计值,设计控制律,为

其中L为控制器正定增益矩阵。
定理 2对于第 γ个采样时刻(γ ≥0),常数l满足条件0 ≤l≤T-1时(T为采样周期),若控制器增益矩阵L满足|||ΦγT+l-F(X)L||<1,且干扰估计值满足时,机器人位置跟踪误差eγT随时间收敛至零,即有

证明将控制律式(29)代入误差函数式(28),得
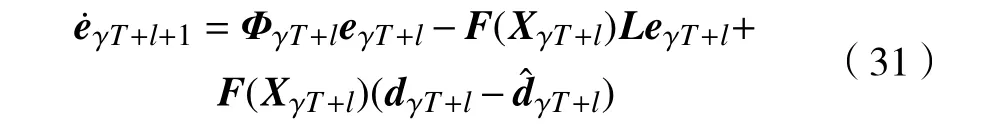
整理式(31)可得
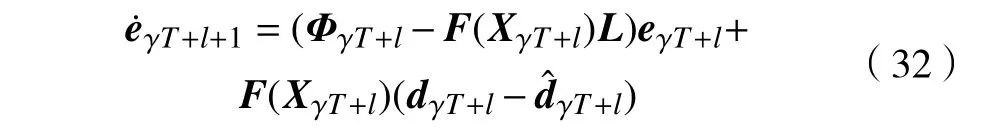
由式(31)和式(32)可以得到:若||ΦγT+l-F(XγT+l)L||<1且 ||dγT+l-γT+l||→0,则对于γ ≥0,0 ≤l≤T-1,有

从上述结论可知,当干扰估计误差 σ趋于零时,调整控制器增益L,可以使系统误差ek随时间k的增大而减小,直到小于最大允许误差ε,即
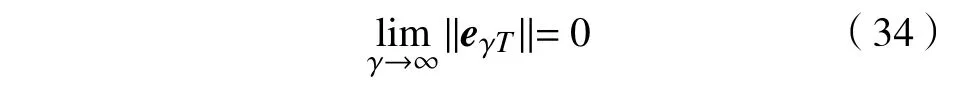
4 仿真
为了验证本文方法对机器人网络控制系统的有效性,选择式(35)机器人作为被控机器人。

式中:机器人2 个关节连杆质量分别为m1=10 kg,m2=5 kg;2 个关节的连杆长度分别为l1=1 m,l2=0.5 m;连杆关节点和连杆质心的距离为r1=0.5 m,r2=0.5 m;重力加速度为g=9.8 N/kg。i1=0.83+。
被控机器人关节1 的期望轨迹为q1=0.1+0.5sin(t),关节2的期望轨迹为q2=0.1+0.5cos(t)。设被控机器人关节初始位置为,式(22)中的 μ取为0.5。
假设系统中存在的网络随机时延,如图3 所示,外部干扰d为图4 所示的方波。

图3 网络随机时延
由图4 可知,在0.3 s 时被控机器人关节1 和关节2 的干扰观测值收敛到稳定状态,干扰观测器能够良好地观测关节1 和关节2 的外部干扰。需要说明的是,在3 s 和6 s 左右时观测效果有瞬间的误差,这是由于方波类型的干扰瞬时突变引起的,但是观测误差很快随干扰突变的消失而减小,又能够继续保持良好的观测效果。

图4 关节1 和关节2 外部干扰观测值
针对存在上述外部干扰以及网络随机时延的机器人网络控制系统,本文采用事件驱动控制方法,在考虑如图3 所示的网络随机时延的同时,对如图4 所示的外部干扰进行补偿,并且与文献[12]中无干扰补偿的事件驱动控制方法进行对比。被控机器人关节1 和关节2 的位置跟踪结果如图5 和图6 所示。
由图5 和图6 可知:对于被控机器人关节1,有干扰补偿的事件驱动控制方法在1.5 s 时取得较好的位置跟踪效果,文献[12]无干扰补偿的事件驱动控制方法在2.3 s 时才能取得位置跟踪;对于被控机器人关节2,在1.1 s 时,有干扰补偿的事件驱动控制可以取得较好的位置跟踪效果,文献[12]则在1.6 s 时才能取得位置跟踪。因此,采用本文有干扰补偿的事件驱动控制方法相较于无干扰补偿的事件驱动控制方法收敛速度更快,能够很好地跟踪期望轨迹。

图5 有干扰补偿事件驱动控制的跟踪轨迹

图6 无干扰补偿事件驱动控制的跟踪轨迹
从图7 和图8 也可以看出,有干扰补偿的事件驱动控制方法使关节1 位置跟踪误差在0.8 s 后收敛到稳定状态,使关节2 位置跟踪误差在0.5 s 后收敛至稳定状态,相较于文献[12]的无干扰补偿事件驱动控制方法,其收敛更快,并且在控制过程中机器人关节位置跟踪稳态误差更小。综上所述,本文控制方法的关节误差更小,且能够更快地收敛到零,并稳定保持在零的附近。

图7 有扰补偿事件驱动控制关节1 和关节2 跟踪误差

图8 无扰补偿事件驱动控制关节1 和关节2 跟踪误差
为了更精确地对比2 种方法的关节位置跟踪效果,计算了关节1 和关节2 的实际轨迹与期望轨迹的误差以及标准方差,其结果如表1 所示。

表1 关节位置跟踪性能定量比较
由表1 可知,当采用有干扰补偿事件驱动控制方法时,机器人关节1 和关节2 的位置跟踪标准方差相较于采用无干扰补偿事件驱动控制方法时分别降低了53.032%和53.034%。
综上所述,在机器人网络控制系统受到外部干扰的情况下,采用事件驱动控制方法,在考虑网络随机时延的同时对干扰进行补偿,具有更好的位置跟踪效果。
5 结束语
考虑外部干扰及网络随机时延的影响下,本文提出了一种基于干扰补偿的事件驱动控制方法,在考虑随机时延的同时,对干扰进行补偿。首先设计了干扰观测器对外部干扰进行估计,然后在控制器中设置一个最大容许误差,并且在每一个采样时刻将被控机器人的实际关节位置跟踪误差与最大容许误差相比较,一旦不满足预设的事件条件,则控制器将计算出新的控制输入来替换原来的控制输入信号,否则控制器保持上一时刻的控制输入。结果表明,所设计的基于干扰补偿的事件驱动控制方法可以使机器人网络控制系统在受到网络随机时延和外部干扰的影响下,仍具有良好的关节轨迹跟踪性能。
然而在实际应用中,网络不仅存在时延、丢包问题,也可能存在各种网络攻击,如篡改消息、伪造、拒绝服务等。因此,对受到网络攻击的机器人网络控制系统的控制问题有待进一步研究。

