考虑随机影响因素的电网饱和负荷概率预测方法

荆林国 荆仲毅 张韶晶 张韶颖

(1. 国网山东省电力公司滨州供电公司 滨州 256610；2. 山东科技大学电气与自动化工程学院 青岛 266590)

1 引言

电网饱和负荷概率预测是电力系统中远景规划最为核心的环节，其中包含最大负荷和电量的预测。研究区域电网电量的饱和时间及规模，既能为规划部门实现智能电网有序发展及区域能源平衡提供决策意见，又能为用户参与电力市场中长期交易提供数据分析支持[1]。在最大负荷预测过程中非常容易受到极端天气的影响，导致难以把握负荷发展规律，电网饱和负荷概率预测过程中的影响因素众多，需要深入研究[2-3]。

张明理等[4]将饱和负荷密度引入至电力系统远景空间负荷的预测中，利用粗糙集与元胞自动机对城市不同种类用地整体变化过程进行模拟，基于不同用地种类土地转换基本规则对规划区范围内未来土地使用种类与面积变化进行预测；根据Logistic饱和负荷概率预测模型对不同用地种类饱和负荷的密度进行预测；最后基于不同用地种类饱和负荷密度与面积对远景负荷分布情况进行预测。方陈等[5]将BP 神经网络和分位数回归模型相融合，设计并构建电网负荷概率预测模型；根据核密度估计法对最大净负荷概率进行计算；最后以上海某区域电网当作实例对所提方法进行验证。陆继翔等[6]将卷积神经网络与长短期记忆相结合对电网负荷进行预测，将大规模历史负荷信息、气象、日期、峰谷电价等数据依据时间滑动窗口设计连续的特征图作为输入，利用卷积神经网络将特征向量提取出来，利用时序序列的方式构建特征向量，同时当作长短期记忆网络(Long short-term memory，LSTM)的输入，接着根据LSTM 网络实现电网短期负荷预测。

当前，国内外对于预测电网饱和负荷概率影响因素的研究只是简单提及到影响因素，没有将这些因素结合到预测过程中。为了使预测结果更加符合电网实际情况，更具精确性，同时增强预测弹性，结合随机影响因素，提出基于粒子群算法的电网饱和负荷概率预测方法，分析直接影响因素和间接影响因素的权重，然后基于印象因素权重完成供电可靠性需求差异性研究，引入粒子群算法将供电需求按照一级元胞进行划分，分成大用户聚集区域、一般负荷区域和旅游供电区域三个类别，实现预测电网饱和负荷概率分区预测。

2 电网饱和负荷概率预测

2.1 电网饱和负荷影响因素分析

在此深入分析饱和负荷的各种随机影响因素，为电网饱和负荷概率预测提供可靠支撑。经综合分析，得到的电网饱和负荷影响因素如图1 所示。

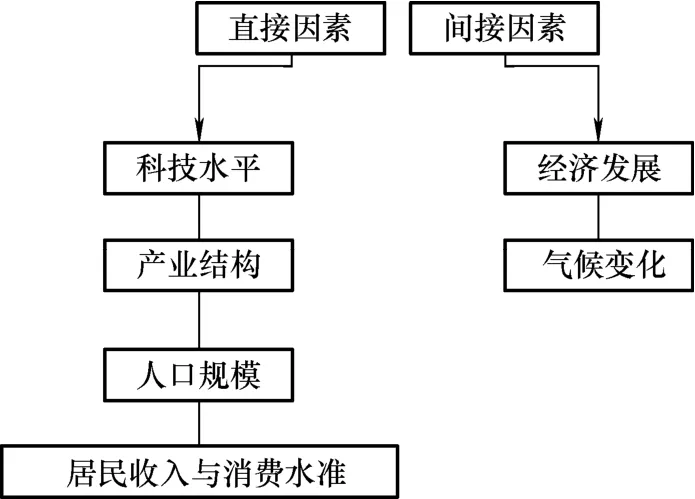
图1 电网饱和负荷影响因素

2.1.1 直接影响因素

(1) 人口规模

人口和经济之间存在紧密关联性，两者之间相互约束且相互影响。根据发达国家与城市电力负荷在饱和阶段的人口规模特征相关研究可知，在某个地区的社会经济处于饱和情况下，电力负荷也会随之进入较为稳定且缓慢的阶段，当人口规模保持较为稳定的状态之前，负荷与人口总量均经历了一个快速发展的阶段。

经济发展相对饱和时，在人均用电量比较接近的状况下，经济整体发展水准与国家或者地区相接近，且产业结构较为相似，人口总规模相对多的地区用电量也相对较大。在同一个国家或地区，电网负荷饱和过程中，人均用电量会处于一个稳定的阶段甚至会降低，随着人口的增多，社会用电总量会持续性增加。

(2) 产业结构

在电网饱和负荷概率预测的各种随机影响因素中，经济结构的调节对于社会电力的整体消费水准与消费结构变化有着很重要的影响，由此该因素对电网饱和负荷有着全局性与基础性的影响。

(3) 科技水平

在科技水平和节能技术不断发展与应用的今天，经济总量持续上升，然而产值单耗不断下降，国民生产的整个过程中设备的总能耗在不断降低。

在科技水平不断发展与国家节能减排绿色发展政策的指引下，生产效率得到了进一步提升，节能技术受到了广泛关注与应用，产值单耗有希望得到进一步减少。科技水平的提升会有效降低产值单耗，且相同产值电量消耗也会变得越来越低。

(4) 居民收入与消费水准

经相关调研结果可知，居民可支配收入越低，则相应居民生活中的用电量也会变低，这反映了居民收入和用电量有着显著的正相关关系，居民的收入高低对人均用电量有直接影响。

2.1.2 间接影响因素

(1) 经济发展

影响电网饱和负荷的因素很多，其中，经济发展水准与经济结构调节很大程度上影响了电力消费水平及电力负荷结构的整体变化。

(2) 气候变化

气温等气候变化对于社会各方面的影响也是不可忽视的，气候变化对于电网饱和负荷影响重大且深远。气候影响因素主要包含气温、湿度、日照等。在工业生产过程中，不受气候影响的通常为不间断的生产模式，由此气候对于工业负荷产生的影响比较小；居民的用电负荷在整个电网系统中占据的比例逐渐增加，且对系统峰值负荷在季节方面的变动具有十分显著的影响；农业负荷会随着气候的不断变化而变化，其中灌溉和干旱阶段的负荷比较大。

2.2 依据不同需求划分供电区域

为了得到更为精准的预测结果，利用改进的聚类算法划分供电区块。聚类算法基本运行原理为依据数据对象的属性，将数据划分成若干个类别，同时使类间差异度尽量大，类内的差异程度尽量小[7-8]。聚类算法运行中，初始聚类中心的选择一般会对聚类结构优良产生直接影响，在传统的聚类算法中通常使用的是随机方式选择聚类中心，致使聚类最终结果不是十分稳定。

在K-均值聚类算法运行过程中，随机选取出k个初始聚类中心，对剩余点和初始点之间的距离进行计算，并将剩余点赋给距离最近的初始点，进而构成k类。使用多级聚类法，基于变电站所处位置将待测区域分解成若干个一级的元胞；以方便供电区域划分为目的，将变电站近似为点，并提出改进K-均值聚类法实现供电区域划分。

设计选择的K-均值聚类算法通过误差平方参数量和误差准则函数作为当前聚类性能的评价方法。对于当前现有的γ维数据集X，每一维都分别代表其现有的描述属性，不包含其独有的类别属性。假设X包含k个数据聚类子集为：X1,X2,…,Xk，则设n1,n2, … ,nk表示各子集中包含的样本数据个数，各个聚类子集的中心点，即为均值代表点，分别设置为m1,m2,…,mk。此时误差平方准则的函数公式为

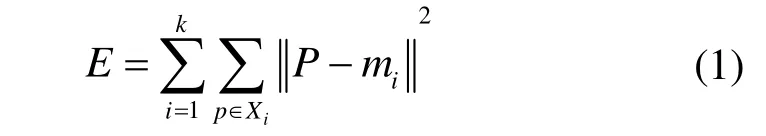
式中，E表示当前数据集下所有数据对象的均值方差总和，p表示当前数据空间下对应数据点，im表示聚类子集下的数据聚类子集X1的数据中心点。

综上，需要先确定下列参数。

(2) 相关参数2：某个变电站r域。将该变电站当作圆心，内部不含有其他变电站的一个最大圆形区，该区域半径为r。将所有变电站r域半径均值记作r。

(3) 相关参数3：密度阈值Zh。对某个区域隶属变电站高密度区域参考值与否进行判断，当以r为半径的圆形范围内含有的变电站数量大于Zh时，将该区域判断为变电站的高密度区。

除上述内容之外，设定两个集合D、M。D、M分别代表处在高密度区域初始聚类中心的各个变电站组成的集合。详细步骤如下所示。

步骤1：信息数据初始化。将各个变电站地理坐标和密度阈值Zh以及初始聚类中心的数量k作为输入，并将D、M设置成空集。

步骤2：对待预测的区域范围内所有变电站两两间的空间距离d(i,j)进行计算。

步骤3：对各个变电站r域和半径均值r进行计算。针对各变电站，将自身当作圆心，将r当作半径构建圆形区域，对圆形区范围内中含有的变电站数量进行统计，假设大于阈值Zh，那么将该变电站放到高密度集合D。将密度最高，也就是圆形区域中含有变电站数量最多的区域记作k1。

步骤4：将k1由集合D迁移至初始聚类中心集合M。

步骤5：对比变电站k1与D中所有变电站间距离。将距离k1最远的变电站筛选出来，将其记作k2，并将k2从D迁移至M。

步骤6：由集合D中找到与k1、k2相差最远的变电站k3，也就是k3和k1、k2距离相加值最大，把k3从D迁移至M。

步骤7：依据上述方式从D中找出与所有初始聚类点距离最远的变电站，同时将其迁移至M，直到M中变电站的数量为k。综上，即可得到k个初始的聚类中心。

步骤8：将获取的k个初始聚类中心当作出发点，通过K-均值聚类法实现供电区域划分，各供电区域块分别与一个一级元胞相对应。

基于供电可靠性需求存在的差异性，将各一级元胞进行划分，分成大用户聚集区域、一般负荷区域和旅游供电区域三个类别。在该过程中，一般负荷区域需要基于功能进行分区，并依据产业结构进一步精细划分，进而生成二级元胞为构建预测模型奠定基础。

2.3 预测模型构建与参数求解

为了适应多随机影响因素变化，引入高斯过程回归模型(Gaussian process regression，GPR)，可以由正态假设的贝叶斯线性回归导出，贝叶斯线性回归假设残差服从独立同分布，由此可得贝叶斯线性回归的似然

将电量及其影响因素的部分历史数据作为训练样本，剩余历史数据作为测试样本，二者共同输入至高斯过程回归模型中，将该模型应用在电网饱和负荷概率预测中的大体思路如图2 所示。

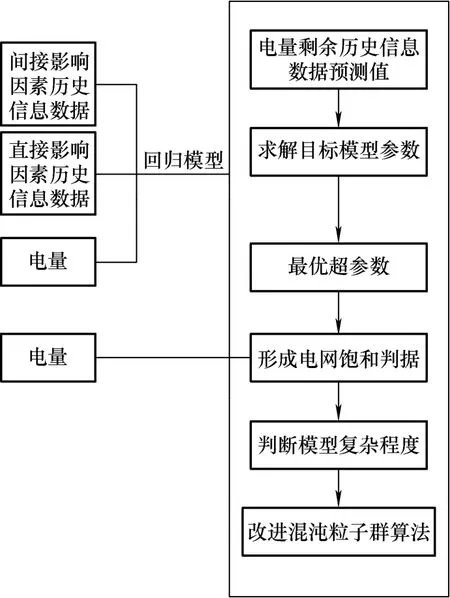
图2 电网饱和负荷概率预测方法设计流程图

将电量及其直接影响因素的部分历史信息数据当作训练样本，将其中间接影响因素历史信息数据当成测试样本，两者一起输入到回归模型中，利用滚动预测的方式获取电量剩余历史信息数据预测值，同时对不同供电区域的影响因素参数进行求解，获得这个供电局域内最大程度随机影响因素的最优超参数；利用电网饱和判据与饱和负荷的随机影响因素规划数值相结合，构建电网饱和负荷概率预测模型。模型如式(4)所示

在模型求解过程中一般用到的方法为共轭梯度法，但是上述模型比较复杂，为此引入改进的混沌粒子群算法对目标模型进行求解，以实现电网饱和负荷概率的预测过程。详细求解过程如下所示。

(1) 混沌粒子群算法基本运行原理

算法运行的基本原理主要是将混沌的特性引入粒子运动整个过程中，通过混沌动力系统具备的遍历与轨迹规律特性实行搜索，进而实现粒子搜索范围与收敛速度的优化，然而因混沌序列存在初值敏感的特性，寻优结果不是十分理想[9-10]。每个粒子可视为N维搜索空间中的一个搜索个体，粒子的当前位置即为对应优化问题的一个候选解，粒子的飞行过程即为该个体的搜索过程。粒子的飞行速度可根据粒子历史最优位置和种群历史最优位置进行动态调整。粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向[11]。每个粒子单独搜寻的最优解为个体极值，粒子群中最优的个体极值作为当前全局最优解。经过不断迭代，更新速度和位置，最终得到满足终止条件的最优解。为解决上述问题，引入带有极值变异的粒子群法，改进过程如下所示。

结合极值变异因子，促进粒子在个体和群体最佳位置进行长时间的停滞并产生变异，防止粒子早熟，使粒子跳出最佳解性能得以优化。

设计并构建混沌控制机制，优化混沌对于初值敏感性和拓宽粒子整体搜索范围[12]。带有极值变异的算法动力学模型可表示为

(2) 混沌控制

按照上述运行思想，在迭代初期阶段，依据基本粒子群算法收敛速度快的特性，暂时不结合混沌变量[13]，优化粒子位置初始值，在迭代中后期阶段，当粒子进入稳定状态时，结合混沌变量，防止粒子早熟，在粒子运动过程中将混沌变量撤走，并让粒子处在个体历史最佳的位置引入极值变异因子，提高收敛速度。

以判断粒子稳定情况为目的，利用式(10)进行判断

(3) 超参数求解

利用改进的混沌粒子群算法对回归模型超参数进行求解，详细过程如下所示。

将和方差作为适应度[14]，基于超参数的约束条件，对粒子群进行初始化。将超参数速度与位置数据与训练样本和影响因素样本当作输入信息输入到回归模型中，并利用式(11)和式(12)滚动预测负荷值测试样本。

对粒子个体位置与群体位置的最佳值进行更新，同时对群体的最佳适应度值满足要求与否进行判断[15]。假设满足条件，则算法运行结束，反之转至下列步骤。

利用式(4)～(7)对粒子速度和位置进行更新，并转至适应度值计算步骤。

在确定超参数之后，出于对电网饱和负荷随机影响因素的考虑，融合饱和判据，设计并构建基于粒子群的电网饱和负荷概率预测模型。

3 试验结果与分析

为验证基于粒子群算法的电网饱和负荷概率预测方法整体有效性，进行一次相关性测试。试验选择某市电网实行饱和负荷概率预测，市规划总面积约2 000 km2，管辖街镇28 个，村居1 223 个，当前常住人口约190 万人。在大区域划分中，一共有30 座110 kV 变电站，27 座35 kV 变电站。小区域划分中，规划总面积与城市建设面积分别为46.65 km2与35.54 km2。将采集的数据输入至Matlab 中，验证所提方法的预测效果。根据非规范拟合指数NNFI与相对拟合指数CFI 两种拟合指标判断模型与数据的拟合程度，反映模型的简易程度与自由度。其中，非规范拟合指数NNFI 作为一种非规范性指标，其规范值在0～1 之间，相对拟合指数CFI 的最优临界值则是0.9，也就是说，其拟合指数越接近1 表示其数据拟合程度越高，简易程度越符合时间电网需求，利用不同文献研究的相关对比结果验证所提方法的预测精确性，验证结果如图3 所示。

图3 不同研究成果NNFI 对比

由图3 可知，本文方法的NNFI 指数高于其他文献研究指数且最接近于1，表明其简易程度符合模型要求，模型更加符合电网实际情况，可增强预测弹性。

以下利用相对拟合指数CFI 检验回归模型返回电量剩余历史信息数据预测值的自由度，测试对比结果如图4 所示。

图4 不同研究成果CFI 对比

图4 从不同研究成果预测结果与实际情况比较拟合指数中可以看出，文献[6]的拟合程度较高，文献[4]的拟合程度最低但在一定程度上高于文献[5]，但本文方法预测值的拟合程度一直高于其他文献，表示其电量剩余历史信息数据预测值有较高的自由度，考虑到随机影响因素的大范围变化，说明基于粒子群算法的电网饱和负荷概率预测方法在返回电量剩余历史信息数据预测值时的精确性要优于其他文献研究成果。主要原因为所提方法有效结合了电网饱和负荷影响因素和供电区域划分，为实际预测提供了可靠支撑，且为了适应多随机影响因素变化，引入高斯过程回归模型构建电网负荷预测模型，并通过混沌粒子群法对模型参数进行了求解，准确实现了电网饱和负荷滚动预测。

为了验证结合本文模型结合随机影响因素的程度与效果，综合考量电网饱和判据与饱和负荷的随机影响因素规划数值，在考虑随机影响因素规划数值的最大影响程度后，以最终饱和规划数值与饱和期望值的比值，验证不同方法的鲁棒性，对比验证结果如表1 所示。

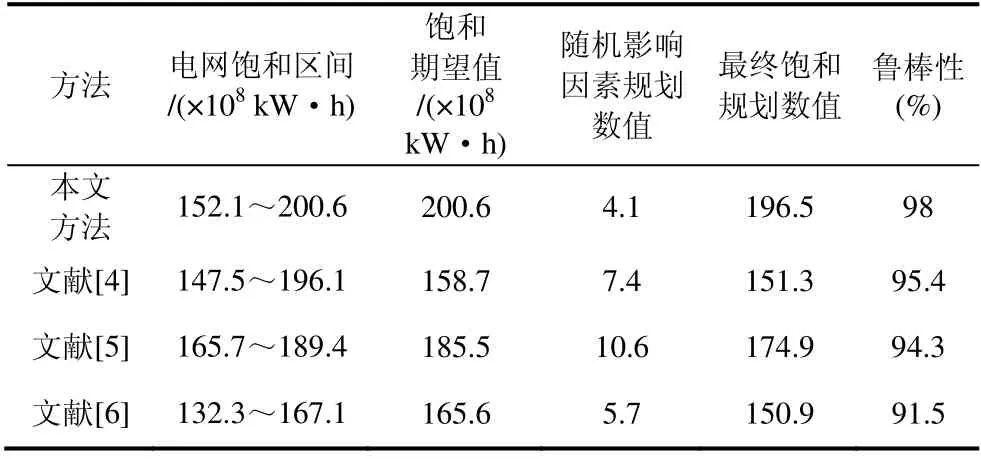
表1 鲁棒性对比验证结果

由表1 可知，本文研究模型的最终饱和规划数值鲁棒性皆强于其他文献研究方法，主要原因在于该方法非标准拟合指数和比较拟合指数均较高，融合饱和判据程度强，预测电网饱和负荷概率可靠性高，可满足电力系统实际需要。

4 结论

电网运行的优良对人们日常工作和生活而言均有着十分重要的意义，因此，提出基于粒子群算法的电网饱和负荷概率预测方法。依据影响因素分析与供电区域聚类划分，引入高斯过程回归模型与粒子群法实现电网饱和负荷概率的预测。试验表明，所提方法预测精度较高，可实践性比较强。下一步可针对预测方法的适用性方面做进一步研究，以更好地满足电力系统实际需要。