储能参与电网辅助调频的协调控制策略研究*
彭 鹏 胡振恺 李毓烜 刘泽健 范紫微
(1. 南方电网调峰调频发电有限公司 广州 511400;2. 深圳华工能源技术有限公司 深圳 518000)
1 引言①
随着传统化石能源的持续消耗和环境问题的日益加剧,以光伏、风电等为代表的清洁新能源迅速得到广泛关注[1-3]。然而光伏、风电这类新能源并不具备传统发电机所具有的惯量和阻尼特性[4-5],其出力具有随机性和不确定性,当其大规模并入电网时势必会冲击电网,加剧电网的调频压力[6]。当前阶段,电网调频主要依赖传统的火电机组和水电机组,二者在参与频率调节时都存在一定不足[7-8],因此引入一种新的调频辅助手段显得尤为必要。
近年来储能技术迅速发展,其快速的响应特性和精确的功率跟踪能力使其在参与电网辅助调频方面具有显著优势[9-11]。目前,针对储能参与电网辅助调频,国内外相关学者在这方面做了大量研究,主要集中在储能参与电网辅助调频的协调控制策略、储能电池的容量配置以及经济性评估等方面,并取得了一些成果。
储能辅助电网调频的协调控制策略主要包括下垂控制和虚拟惯性控制[12],前者能够有效减小系统稳态时的频率偏差,后者能够有效抑制系统频率变化率。为充分利用这两种控制的优势,文献[13]提出一种储能参与电网一次调频的自适应控制策略,实现了两种控制策略的平滑切换;文献[14]将储能参与二次调频的两种常见控制方式优缺点进行分析,并择其二者优点,进而提出了一种综合的控制方式,确定了储能的最佳出力时机与动作深度;针对储能参与电网一次调频时,文献[15]提出通过给储能设置恰当的调频死区,减少了传统调频机组在一次调频死区附近的频率波动。
在储能参与电网辅助调频容量配置和经济性评估方面,文献[16]采用在储能出力上实时叠加一个额外充放电功率的方法,提出了一种储能调频容量配置的最优化策略;文献[17]将风电机组等效为负荷,研究储能对频率偏差的影响,并以频率偏差的均方根值和绝对最大值两项指标为依据来配置储能容量;针对储能参与二次调频的容量配置问题,文献[18]利用定时间常数滤波法将从调度中心获得的调频信号划分为高频和低频部分,通过利用储能承担其中的高频分量来对储能的调频容量需求进行分析;文献[19]以含水、火电厂以及风电的电网为背景,以电池储能产生的年效益最大为目标,建立经济评估模型,并提出一种容量和运行方式优化方案,用净现值法评估储能配置方案的经济性。
综观上述研究成果,对储能参与电网辅助调频具有一定的指导价值,但是以上研究并未从储能层面去考虑储能在参与电网辅助调频时的荷电状态(State of charge,SOC),也未对储能SOC 进行明确分区来避免深度充放电对储能的寿命影响。因此本文针对以上问题,在充分考虑储能的SOC 状态管理基础上,对储能的SOC 及电网频率偏差进行分区,提出了一种储能与传统调频机组联合参与电网频率的协调控制策略,并通过仿真算例验证了所提控制策略的有效性。
2 电池储能参与电网辅助调频系统建模
2.1 储能系统建模
电池储能系统(Battery energy storage system,BESS)一般由电池模块、能量转换装置(Power conversion system,PCS)、电池管理系统(Battery management system,BMS)、监控保护系统等几部分组成,如图1 所示。
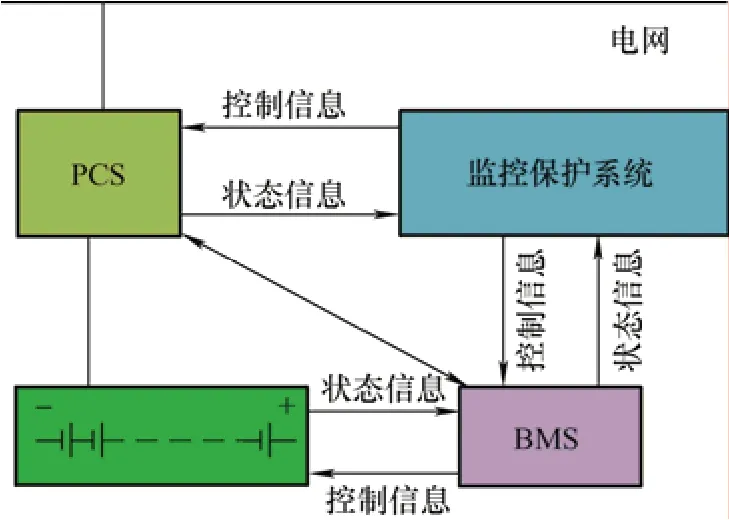
图1 电池储能系统的结构示意图
在BESS 参与电网辅助调频时,常常用一阶惯性环节和比例环节相乘来模拟BESS,其输入输出的传递函数如图2 所示。其中,Δf为频率偏差,作为BESS 的输入, ΔPb(s)为输出信号,作为其参与电网调频时的有功出力。Kb为储能电池的频率调节效应系数,Tb为一阶惯性环节中的时间常数。

图2 电池储能系统的传递函数
2.2 含储能系统的电网调频模型
一个区域电网系统主要由发电机组及其附带的控制系统、配电网、负荷等部分构成。将BESS 引入到电网调频模型中,能够有效改善电网的频率特性。典型的含BESS 的区域电网调频模型如图3 所示。主要包括发电机组调速器模型、汽轮机模型、储能系统模型以及系统惯性和负荷频率特性模型。其中,ΔPC(s)为电网二次频率调节时所输入的功率,ΔPL(s)为负荷功率扰动量,Δf(s)为电网频率波动量,kg为发电机组的单位调节功率,M和D分别对应系统惯性时间常数和负荷频率特性系数。Ggov(s)、Gen(s)和GB(s)分别为发电机组调速器模型、汽轮机模型以及BESS 模型。
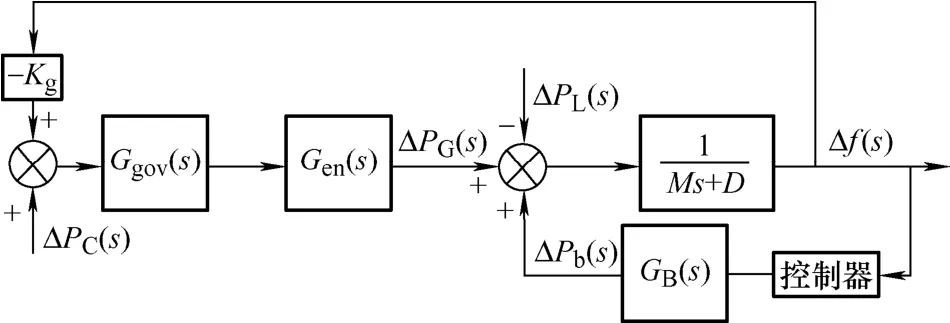
图3 含电池储能系统的电网调频模型
3 储能参与电网调频的协调控制策略
3.1 协调原则
BESS 在参与电网频率调节时,为充分发挥储能的优势和最大限度减小系统频率偏差,关键在于BESS 与传统调频机组的协调控制。其协调具体原则如下所示。
(1) 当系统频率偏差在小范围内变化时,为了减小传统调频机组频繁动作参与调频对机组的磨损,常常需要设置一个调频死区。在调频死区范围内时,考虑到频繁充放电对BESS 使用寿命的影响,此情况下BESS 不参与频率调节。
(2) 频率死区范围内,考虑BESS 在下一个调频周期具有充足的可调容量,需要观察SOC 状态,对BESS 进行充放电操作,使得SOC 向基准值靠拢,SOC 基准值一般取为0.5。
(3) 当频率偏移到死区范围外,且未超过电网所允许的最大频率偏差范围时,利用BESS 的快速功率吞吐能力特性,BESS 参与频率调节,同时也考虑SOC 状态。
(4) 当频率偏移到电网所允许的最大偏差范围外时,BESS 以最大功率进行充放电,优先保证调频需求。在传统调频机组响应调频需求逐渐增加出力时,BESS 在慢慢减小充放电功率,直至电网达到新的平衡态时BESS 退出运行,以确保BESS 的SOC 运行在合理范围。
3.2 储能参与电网调频的控制策略
为实现BESS 与传统调频机组的协调控制,对系统频率偏差范围进行分区,如图4 所示。其中,f0表示系统额定频率,Δf1表示系统频率死区,Δf2表示电网频率允许偏差的最大范围。
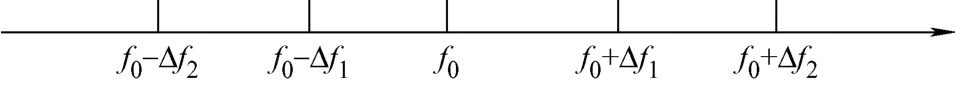
图4 频率偏差分区
针对BESS 的充放电特性,也对其SOC 进行分区,并对其赋值,如表1 所示。其中,SOChigh、SOClow、SOCmax、SOCmin分别表示BESS 充放电时的较高值、较低值、运行上限和运行下限。

表1 BESS 的SOC 分区取值
基于以上分区可得到BESS 与传统调频机组参与调频的具体协调控制策略如下。
(1) 当f∈ [f0-Δf1,f0+Δf1]时,传统调频机组与BESS 都不参与系统频率响应。若SOC 偏离基准值,则对BESS 进行充放电操作,使其SOC恢复到基准值附近。BESS 充放电的功率如式(1)所示

式中,Pbess为BESS 的充放电功率;Prated为BESS的额定充放电功率;Ke为BESS 的充放电系数,取值范围为0~1。

2) 当 SOC 处在区间[SOClow,SOC1]和[SOC2,SOChigh]时,利用BESS 快速的响应特性优先承担频率调节任务,其出力可按式(3)和式(4)选取
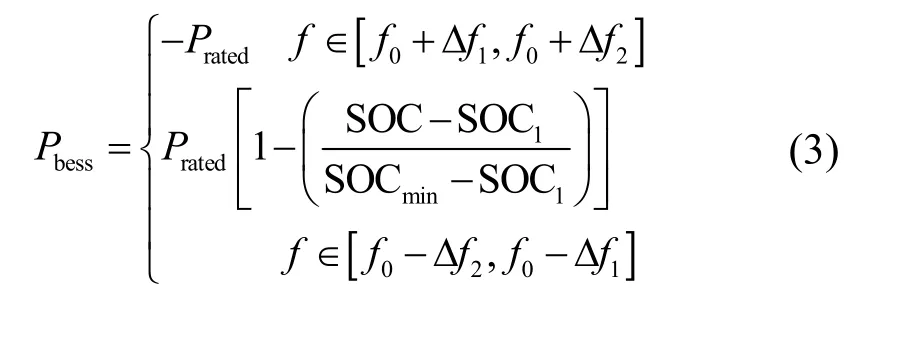

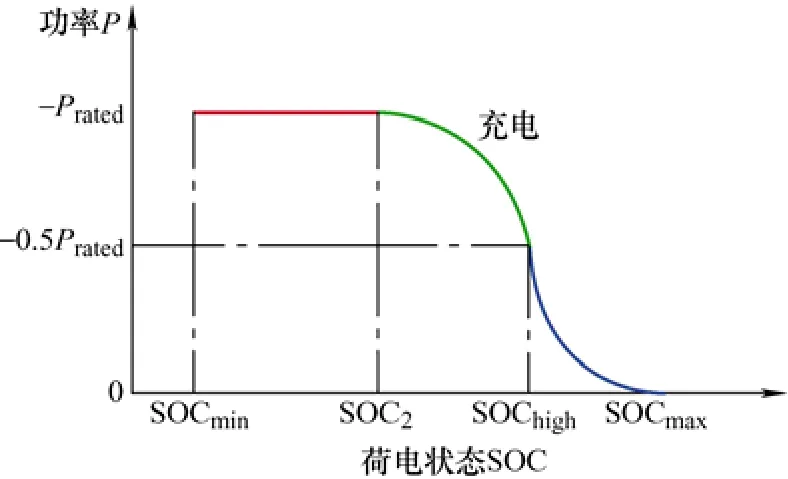
图5 BESS 的充电过程

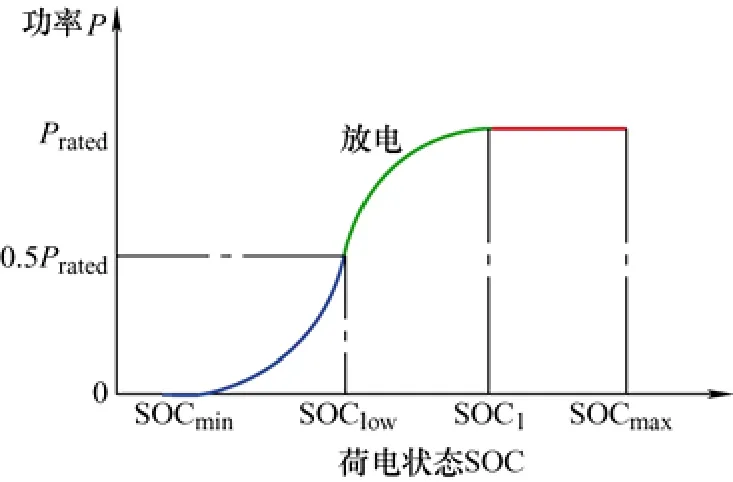
图6 BESS 的放电过程

式中,α、β分别表示BESS 和传统调频机组的出力分配系数。
整个调频过程出力如图7 所示。t0时刻,系统发生负荷功率ΔPL扰动,BESS 与传统调频机组开始动作;t1时刻,BESS 率先达到额定功率并继续保持出力,传统调频机组出力继续增加;到t2时刻时,BESS 与传统调频机组出力之和完全抵消负荷功率扰动量;此后传统调频机组出力继续增加,而BESS 出力则开始减小,直到t3时刻,传统调频机组出力完全抵消负荷功率扰动量,BESS 完全退出运行。
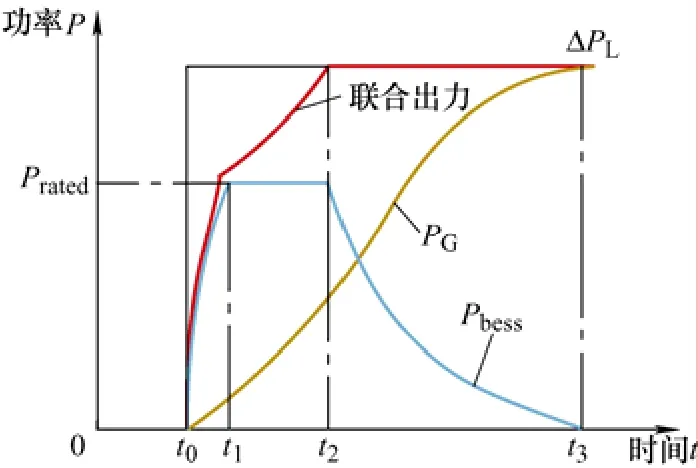
图7 储能和传统机组出力示意图
所提BESS 参与电网调频的控制策略流程图如图8 所示。
4 仿真算例
为验证本文所提出的BESS 与传统调频机组参与电网调频的协调控制策略,在Matlab 仿真中搭建了如图3 所示的含储能电网调频等效模型,其仿真模型中的参数设置如表2 所示。

表2 仿真参数设置
仿真中通过Matlab 中的模块来模拟负荷扰动功率,分两种工况来对BESS 参与调频的效果进行分析:① 阶跃负荷扰动下,有BESS 和无BESS 参与电网调频的对比分析;② 连续负荷扰动下,有BESS 和无BESS 参与电网调频的对比分析。
4.1 阶跃负荷扰动下BESS 参与电网调频
初始时刻,系统稳定运行,1 s 时,给系统突增一个阶跃扰动功率,系统的频率以及BESS 和传统调频机组的出力如图9 所示。
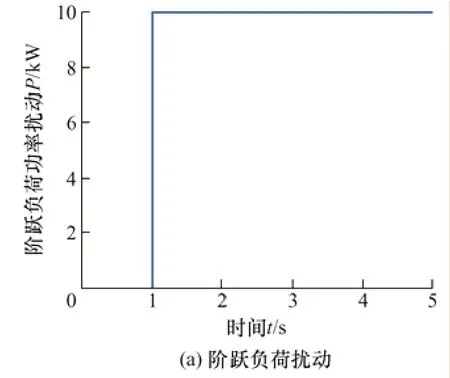
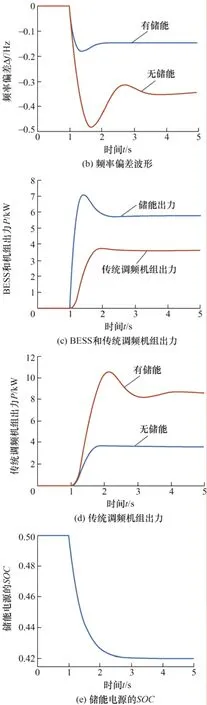
图9 阶跃负荷扰动下的仿真波形
从图9b 可以看出,当系统出现功率扰动时,有BESS 参与系统调频时,系统的频率偏差值相较于无BESS 时有所减小,且达到系统有功平衡的时间也大大缩短。这主要是由于BESS 的快速响应特性,能够在系统出现功率扰动时,快速检测出频率偏差,并通过PCS 将储存的化学能转换为电能输送到电网中,维持系统有功平衡。从图9c 和9d 可知,BESS 参与电网调频时,传统调频机组的调频容量大幅降低。从图9e 可以看出,采用本文所提的协调控制策略,BESS 的SOC能够保持在理想区间范围。
表3 表示有储能和无储能时系统频率偏差以及传统调频机组出力的对比结果。

表3 阶跃负荷扰动下有储能和无储能的对比
从表3 的对比结果可知,当系统出现功率扰动时,无BESS 时系统频率偏差达到了0.36 Hz,而有BESS 时系统频率仅偏移了0.13 Hz,与前文的理论分析相符,即当BESS 检测到系统频率偏差时,快速调整其出力,避免了系统频率的进一步下降。由于本文所提控制减小了最大频率的偏差值,因此传统调频机组的最大出力值也相应减小为3.8 kW,即减小了传统调频机组的调频容量。而在无BESS 时,传统调频机组出力达到了8.2 kW。同时系统在受到扰动时,有BESS 相比无BESS 时系统达到功率平衡的时间缩短了1.8 s。
4.2 连续负荷扰动下BESS 参与电网调频
利用Matlab 模块中的随机信号发生器模拟负荷的连续扰动,观察有BESS 和无BESS 参与调频时系统的频率变化情况如图10 所示。
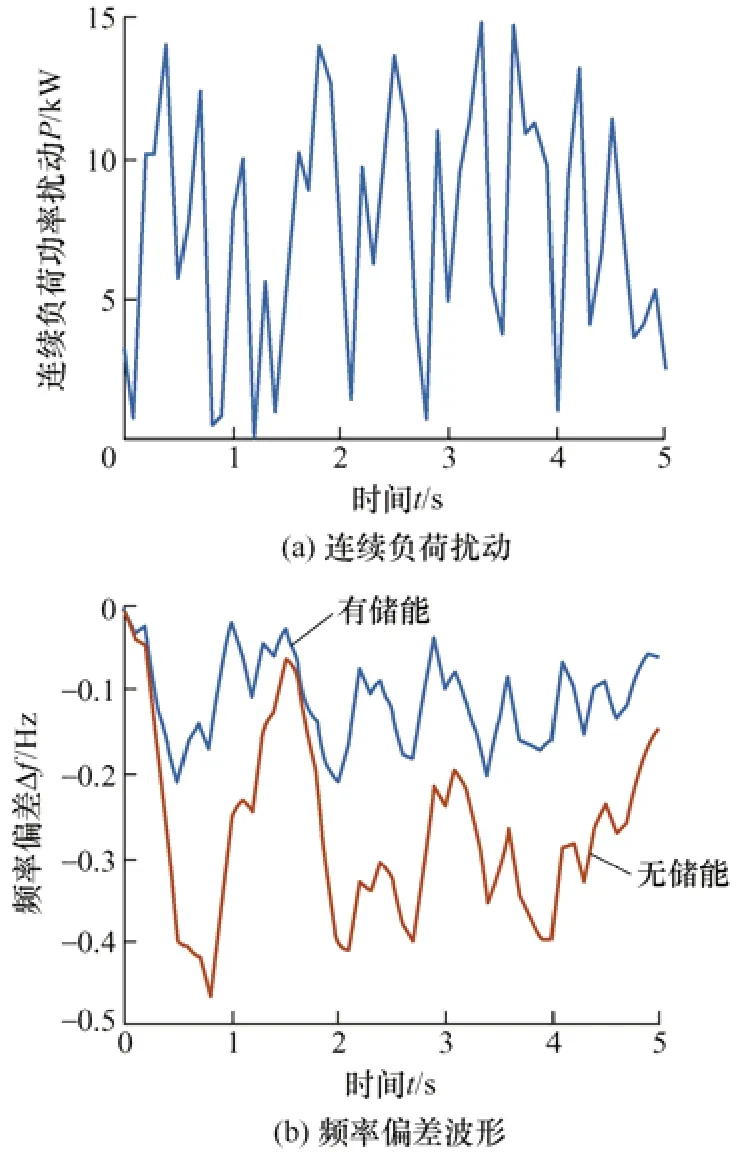
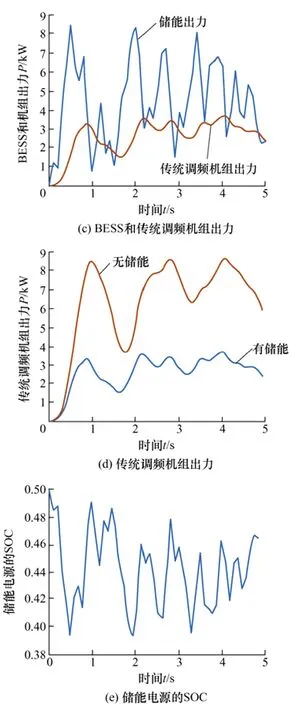
图10 连续负荷扰动下的仿真波形
从图 10 可以看出,在连续负荷扰动情况下,BESS 未参与电网调频时,系统频率偏差较大,最大达到了0.48 Hz,而有BESS 参与调频时,由于BESS 的快速响应特性,系统频率偏差大幅降低,偏差保持在0.15 Hz 左右,如图10b 所示。从图10c 和10d 可以看出,BESS 参与电网调频时,能够有效降低传统调频机组的调频容量,传统调频机组出力在3 kW 左右波动,而没有BESS 参与电网调频时,传统调频机组出力波动较大,最大达到了8.5 kW。从图10e 可以看出,采用本文所提的协调控制策略,BESS 的SOC 能够保持在理想区间范围,避免了对BESS 的深度充放电。综上所述,有BESS 参与电网调频时的频率效果明显优于无BESS 时。
表4 表示有储能和无储能时系统频率偏差以及传统调频机组出力的对比结果。
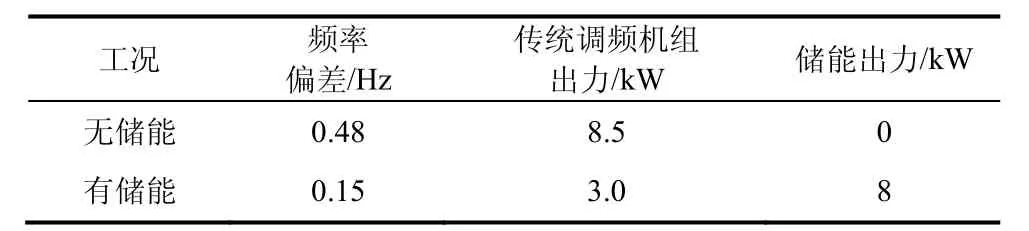
表4 连续负荷扰动下有储能和无储能的对比
从以上仿真结果可以看出,采用本文所提的储能调频控制策略,在阶跃负荷扰动和连续负荷扰动工况下,相比于无储能参与调频时,系统的频率偏差较小,系统达到稳态的时间大大缩小,稳态后传统的调频机组最大出力也明显降低,减小了传统调频机组的调频容量。总的来说有BESS 参与电网调频时的频率效果优于无BESS 时。
5 结论
本文针对BESS 参与电网辅助调频时,提出了一种BESS 与传统调频机组共同参与电网频率调节的协调控制策略,并基于Matlab 仿真对所提控制策略进行了验证,得出以下结论。
(1) BESS 参与电网调频时,在面对阶跃负荷和连续负荷扰动时,相比于无BESS,系统频率偏差减小了0.23 Hz,系统频率达到稳态的时间也缩短了1.8 s。
(2) 含BESS 参与调频的传统调频机组,其调频容量降低了53.6%,参与调频的动作次数减少了57.7%。
(3) BESS 参与电网调频时,通过将其SOC 状态考虑在内,始终能将其SOC维持在理想区间0.4~0.5 内,避免了对BESS 的深度充放电,有助于延长BESS 的使用寿命。

