基于IPMOCSA 的光伏微网混合储能容量优化配置*

王红艳 王依妍 陈景文 肖 妍 莫瑞瑞

(1. 陕西科技大学信息与网管中心 西安 710021；2. 陕西科技大学电气与控制工程学院 西安 710021)

1 引言

微电网作为分布式电源接入电网的一种有效手段，已被广泛应用[1]。微电网中的分布式电源以风电、光伏等间歇性电源为主，由于其波动性，影响微电网的稳定运行，降低其电能质量。而储能介质的引入在提高自发自用比率，平抑可再生能源的波动、改善电能质量及提高供电可靠性方面具有显著作用[2]，但储能装置的引入会增加微电网系统的投资成本，因此需要在保证最大化利用新能源的前提下选择合适的储能容量，降低成本、提高系统的经济效益[3-4]。

目前，越来越多的学者在研究和实施以经济性为目标的混合储能容量优化配置问题，由于目标的多样性为求解带来很大的困难，促进了智能算法的广泛应用，常用的算法有遗传算法、粒子群算法(Particle swarm optimization, PSO)等。文献[5]以功率波动最小目标，采用改进遗传算法进行优化，实现系统的经济性和供电可靠性；文献[6-7]通过遗传算法进行储能功率分配，求解储能经济模型，得出最优配置结果。文献[8]考虑线路损耗和分时电价等影响建立多目标优化模型，利用改进遗传算法对目标求解，确定储能容量配置；文献[9]运用自适应粒子群算法，以成本最低、可再生能源功率平滑最好为目标，对混合储能容量进行优化配置，确保系统的可靠性；文献[10-11]利用改进粒子群算法求解目标，确定混合储能最优配置容量；文献[12]以混合储能系统中直流母线功率波动最小储能容量比最优为目标，利用改进粒子群算法进行容量配置，实现系统经济性。

以上两种主流算法虽可以进行多目标寻优，但其参数设置较多、寻优求解过程较复杂，另一方面，相对都属于贪婪算法的遗传算法和粒子群算法，乌鸦搜索算法被认为是一种非贪婪算法，相比贪婪算法更能增加新一代种群的多样性，从而保证了优化过程的多样性，并且已经证明乌鸦搜索算法(Crow search algorithm, CSA)相比传统优化算法的精度更高、收敛速度更快，但其在位置更新时存在一定盲目性[13-14]。因此，本文提出一种改进的多目标乌鸦搜索算法(Improved multi-objective crow search algorithm, IPMOCSA)来精确容量配置优化结果。

本文在容量配置时，将能量型电池和功率型电池相结合，以达到在满足储能的同时获得最佳经济性的目的。考虑分时电价设计微电网系统的运行策略，建立系统的运行成本模型，精确了微电网的运行成本并建立不同类型储能介质的投资模型。利用提出的IPMOCSA 对多目标进行求解，获得在经济最优时能量型电池和功率型电池的容量配比，最后通过算例分析，证明改进算法的有效性。

2 系统结构及运行策略

2.1 光伏微网系统结构

图1 为光伏微网系统结构，主要包括光伏发电系统、混合储能系统、电网和负荷等几部分，各部分通过变流器互相连接。

图1 光伏微网系统结构图

2.2 微电网运行策略

根据光伏、储能及负荷特性，并考虑分时电价，给出微电网运行策略。以一天为依据，间隔时间为1 h，其运行模式主要分为6 种模式(M1～M6)，如表1 所示。

表1 微电网运行模式

ΔP为光伏和负荷之间的电量差，SOCNmax、SOCNmin分别为能量型电池荷电状态的上下限；SOCGmax、SOCGmin分别为功率型电池电荷状态的上下限；Pricemin、Priceave、Pricemax分别为电网低谷电价、平时段电价和峰时段电价。低谷电价时依靠电网供电，在平时段电价和峰值电价时，光伏优先供电，当光伏有余且储能电池饱和状态，则余电上网，光伏不足时储能放电保证系统稳定运行。

3 系统经济优化模型

以经济性为目标建立并网型微电网系统优化模型，包括微电网运行成本模型和储能投资模型。微电网运行成本主要通过其和大电网的交互功率产生。储能投资模型包含储能安装成本模型、年运行维护成本模型以及置换成本模型。

3.1 微电网运行成本模型

微电网运行成本模型建立在运行策略及储能容量确定的基础上。本文为实现光伏能量最大化利用，在平时段和峰值电价时不考虑电网提供的能量，系统的不平衡功率如式(1)所示

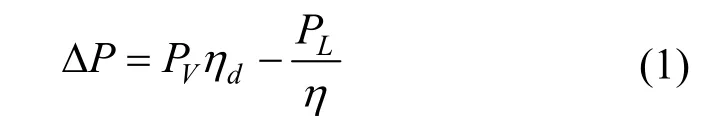
在储能运行时间内，ΔP＞0 时，系统按照M3运行；ΔP＜0 时，系统按照M5 运行以补充负载的缺额，如式(2)所示

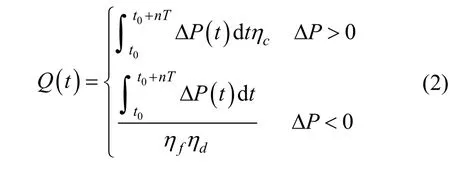
式中，ηc为储能的充电效率；ηf为储能的放电效率；t0为储能运行起始时间(取0～23 h)；T为时间间隔取1 h；Q(t)为t时间内储能充电或放电量。

则储能运行时间内所要存储的最小容量为式(2)中两者较大的，如式(3)所示，当t0分别取0～23 h所得出的Q之和就为考虑分时电价时储能储存的最小功率。

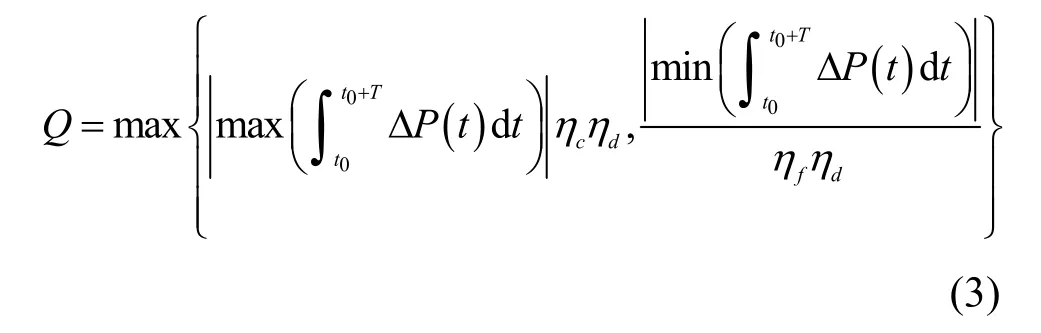
本文所涉及的运行成本，不考虑储能上网、储能存储的电价成本，只考虑电网和微电网交互功率的成本。据前文考虑电网分时电价下的微电网运行策略进行运行成本建模。在电网低谷电价时电网优先给负荷供电，平时段和峰谷电价时，优先光伏供电，供电不足储能补充，否则储能存储并将多余电能上网售卖。

则根据所设计的微电网运行策略，运行成本模型如式(4)所示

式中，yI～yVI分别为6 种运行模式下微电网的运行成本；h(t)为电网分时电价；hV为光伏上网价格；QV为光伏发电量；QL为负荷用电量；η为逆变器的效率；ηd为DC-DC 变换器的效率。

则微电网只考虑和大电网的交互功率的情况下，总的运行成本Cy为

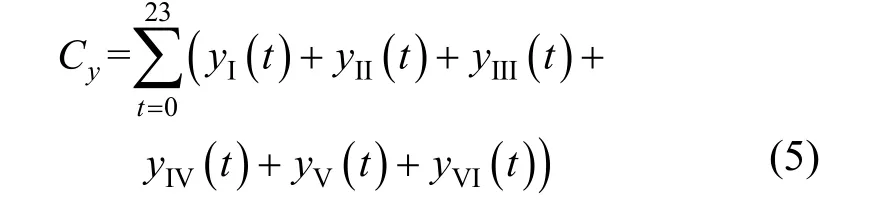
为保证电网的稳定需要对微电网和大电网传输功率及系统功率平衡进行约束，如式(6)和式(7)所示

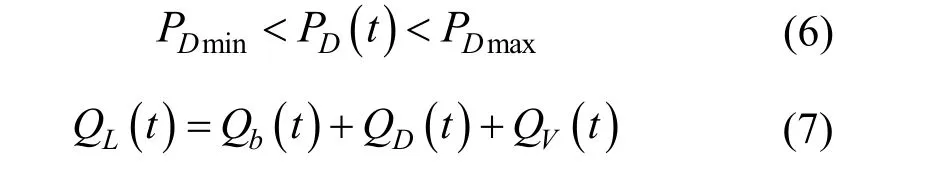
式中，PD为微电网与大电网之间传输的实际功率；PDmax、PDmin分别为两者传输功率的上下限；Qb为储能系统实际放电或充电量，Qb＞0 为正充电，Qb＜0为负放电。

由于电池过充过放会造成电池寿命的损失，应控制电池的荷电状态以及充放电功率。

SOC 充电和放电的荷电状态可以用式(8)表示，则约束为式(9)所示

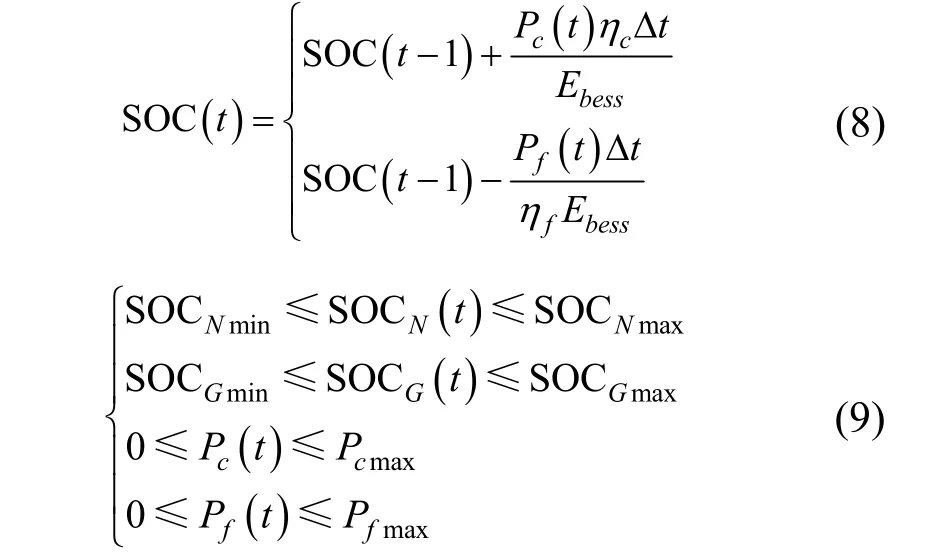
式中，Pc、Pf分别为储能实际充、放电功率；Pcmax、Pfmax分别为储能充、放电功率上限。

3.2 储能投资模型

3.2.1 安装成本模型

安装成本主要包括能量型电池和功率型电池成本、辅助器件成本以及DC/DC 变流器成本。

式中，Cb为电池成本；cg、cc分别为电池单位价格(元/kW，元/(kW·h))；Pbess、Ebess分别为电池功率和容量；α为贴现率(%)；τ为项目周期(年)；Ch为DC/DC 变换器成本；ch为DC/DC 变换器单位价格(元/kW)；Cq为辅助器件成本；cq为辅助器件单位价格(元/(kW·h))。

3.2.2 年运行维护成本模型

储能系统的维护成本较为复杂，包括日常运行中合理之处的维护、管理、人工及相关升级改造成本等[15]，本文只计算固定成本，则储能单元年运行维护成本Cm为

式中，cf为年电池单位维护成本(元/(kW·a))。

3.2.3 置换成本模型

电池的置换频率和其寿命有很大的关联，而实际使用过程中一般达不到理论寿命，因此置换成本模型考虑电池放电深度和放电效率的影响，因超级电容循环寿命高达50 万～100 万次[16]，故认为其不受前者影响，只考虑能量型电池。

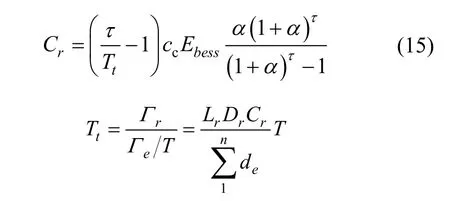
式中，Cr为电池置换成本；Tt为锂电池根据实际放电情况折合的寿命，Dr为锂电池的额定放电深度；Lr为锂电池在Dr和额定放电电流下的失效循环次数；Cr为锂电池在额定放电电流下的容量(A·h)；de为实际放电量(A·h)；T为能量型电池的运行时间。

综上所述，储能系统的最优经济模型为

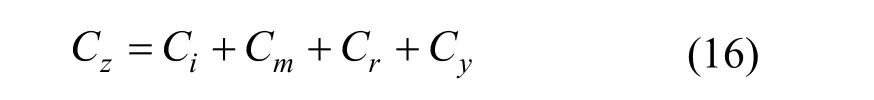
式中，Cz为总成本。

4 模型求解

4.1 乌鸦搜索算法

乌鸦搜索算法是 ASKARZADEH 等[17-18]在2016 年引出的一种模拟乌鸦群体觅食的一种新型智能优化算法，是一种解决复杂工程优化问题的较好方法。CSA 通过模拟乌鸦获取食物的行为进行寻优，种群中所有乌鸦都可以表示优化问题的可行解，乌鸦i试图跟踪乌鸦j并掠取j隐藏点m的食物，在这种情况下有两种可能。

(1) 乌鸦j未发现乌鸦i，则乌鸦i找到食物如式(17)所示

式中，xi,t为乌鸦i第t次的位置信息；ri、rj为[0，1]间的随机数；fli,t为步长；mj,t为乌鸦j食物藏匿位置；APj,t为乌鸦j的感知率。

4.2 改进乌鸦搜索算法

由于CSA 为随机搜索跟踪，不能保证乌鸦i所跟踪的乌鸦j藏匿食物的地方为优，使算法有一定的盲目性。针对算法中存在的问题，在此引入粒子群中粒子向群体最优粒子学习的思想，降低CSA 搜索的盲目性，加快CSA 的收敛速度。

在乌鸦算法位置更新中，引入全局最优的乌鸦，使得乌鸦在跟踪某个乌鸦的同时参考群体最优乌鸦，并向其靠拢以此更新自身位置，式(19)即为引入群最优粒子的位置信息，则乌鸦在没有发现跟踪者的位置更新如式(20)所示

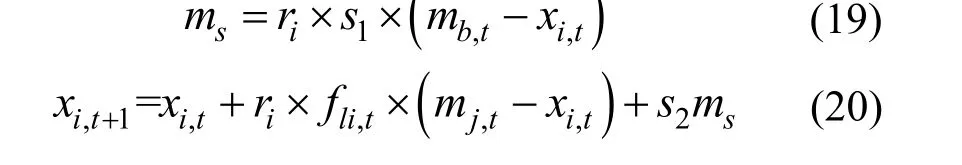
式中，ms为群体最优位置对乌鸦更新位置的影响；s1、s2为权重因子，这里取0.5；mb,t为乌鸦种群中最优位置。

其次，对于飞行步长fli,t来说，当其小于1 时，算法容易陷入局部最优，当其大于1 时，算法全局搜索能力强，但收敛能力慢。为改进乌鸦的寻优能力，同时保证种群的多样性，降低算法的寻优复杂性，避免陷入局部最优，引入莱维飞行思想，莱维飞行能够在算法前期长距离进行飞行促进算法的多样性和全局搜算能力，在后期短距离飞行加快算法的收敛速度，如图2 所示。

图2 步长变化示意图

4.3 求解算法比较与确定

本文分别以粒子群算法、乌鸦搜索算法及改进乌鸦搜索算法对同目标函数进行优化。对比结果如图3 所示。

本次寻优迭代次数为50，种群数量为100，从图3 可以得出，粒子群算法在26 次迭代时收敛于80.67，乌鸦算法迭代21 次后收敛于80.70，而改进乌鸦算法迭代13 次后收敛于80.71，收敛速度大大提高，寻优精度也高于粒子群算法和乌鸦算法。因此本文选用改进乌鸦算法进行容量优化配置。

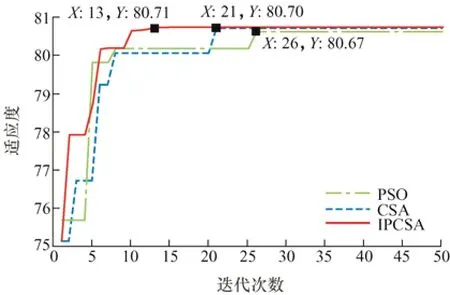
图3 算法比较

求解目标如式(27)所示

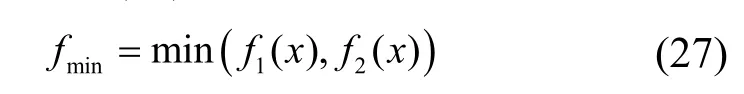
式中，f1(x)和f2(x)分别为能量型和功率型电池经济目标，求解量为各自储能容量、经济成本以及占比；fmin为经济最优成本。

将 IPCSA 引入多目标进化算法中，则IPMOCSA 算法流程如图4 所示，首先初始化乌鸦种群(包括种群数量、飞行步长、感知率、权重因子及迭代次数s)，乌鸦的隐藏食物的位置认为是非劣解(Pareto 解)；其次进行目标函数评估得出最优位置(认为全局最优乌鸦)作为乌鸦位置更新中共享位置；随机选择一只乌鸦j，对感知率进行评判，按照式(21)进行位置更新得到新的种群R，计算R的适应度，检查解的可行性并对乌鸦位置评判；构造P∪R非劣解集，并对解集中非劣解的数量进行约束，确定最终非劣解；最后，判断是否达到停止标准(迭代次数达到设置的最大值为终止条件)，若是输出最终结果完成优化过程，否则选择在Pareto 解集中选择P个乌鸦重新进入目标函数的评估，如此循环。

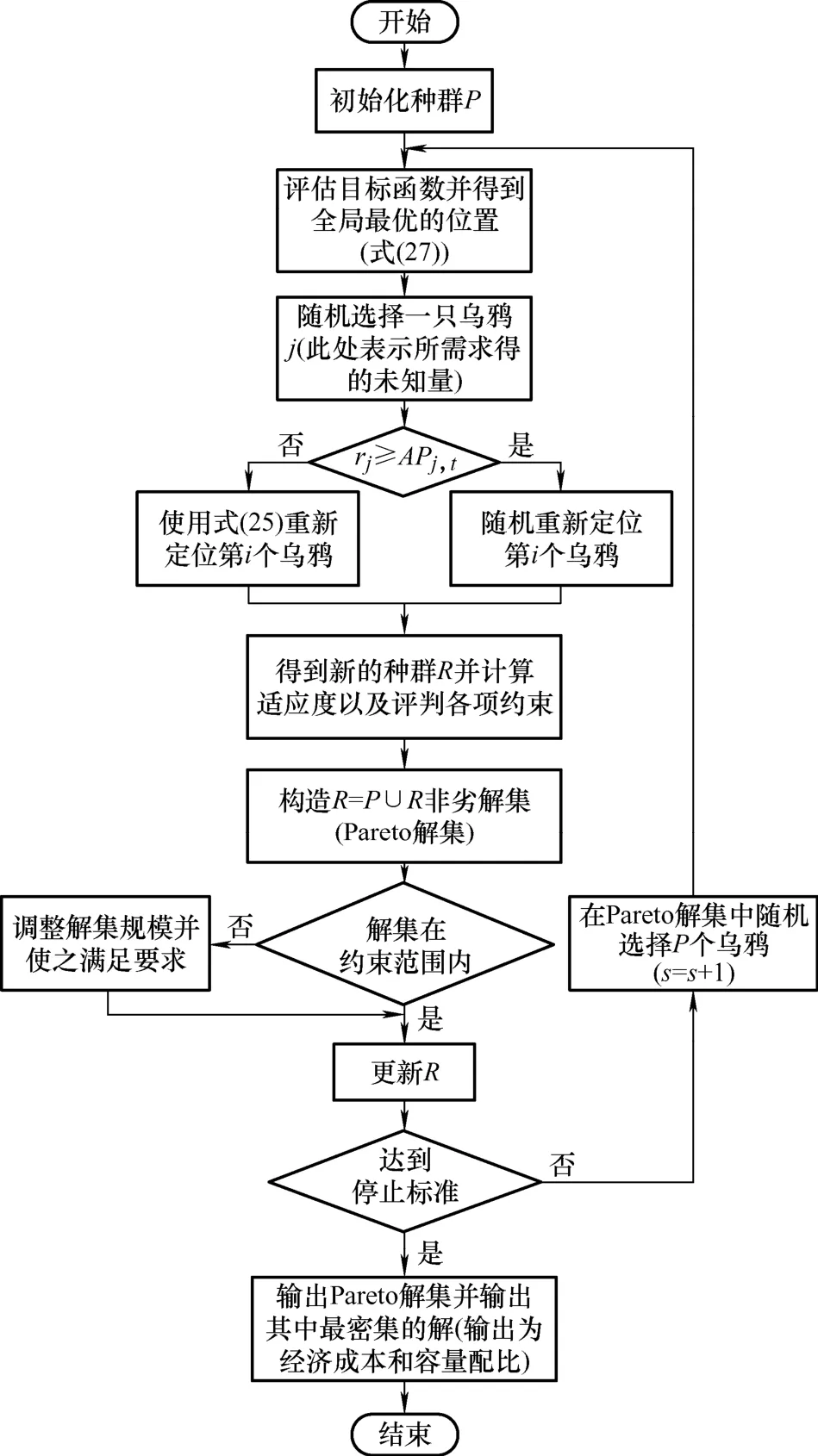
图4 改进的多目标乌鸦算法流程图

5 算例分析

为证明改进乌鸦搜索算法的有效性，以某地一商业楼2019 年用电负荷作为容量优化配置的依据，选取一年内四个季节的典型日用电负荷曲线如图5所示，图6 为光伏电站一年内日累计发电量，为使配置的混合储能满足所有工况负荷用电需求，算例选取四季中日负荷最大的一条曲线进行研究，并综合全年日发电量，将典型光伏曲线作为光伏电站发电依据，具体如图7 所示，包括日负荷曲线、典型日光伏曲线和分时电价曲线。

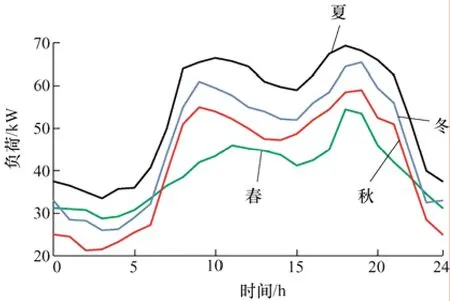
图5 典型负荷曲线

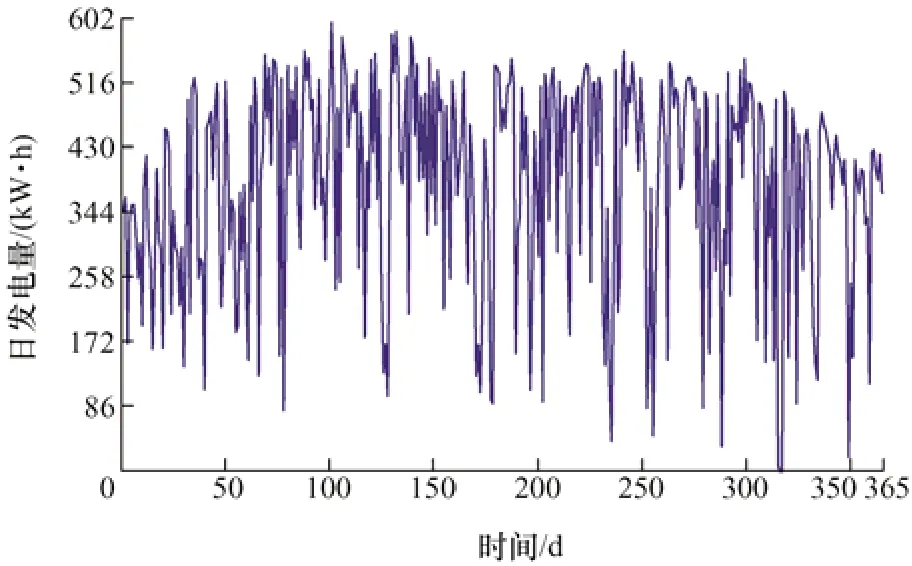
图6 全年日发电曲线

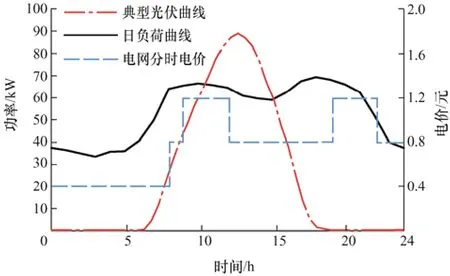
图7 典型光伏负荷曲线

从图7 可得出，在0～8 h 时，电网电价处于低谷阶段，为使所配置储能容量最小，经济最优，由电网给负荷供电，而在8～9 h、12～19 h、22～24 h电网处于平价阶段，9～12 h、19～22 h 处于峰时电价阶段，这两个阶段不考虑电价因素，由光伏和储能共同给负荷供电，以此可以得到在满足全年所有日负荷时，储能所配置的最小容量。

储能各参数如表2[19]所示。项目周期为20 年，贴现率0.1，对功率型电池寿命采用理论值计算。其中，功率型电池采用超级电容，能量型电池采用锂电池。

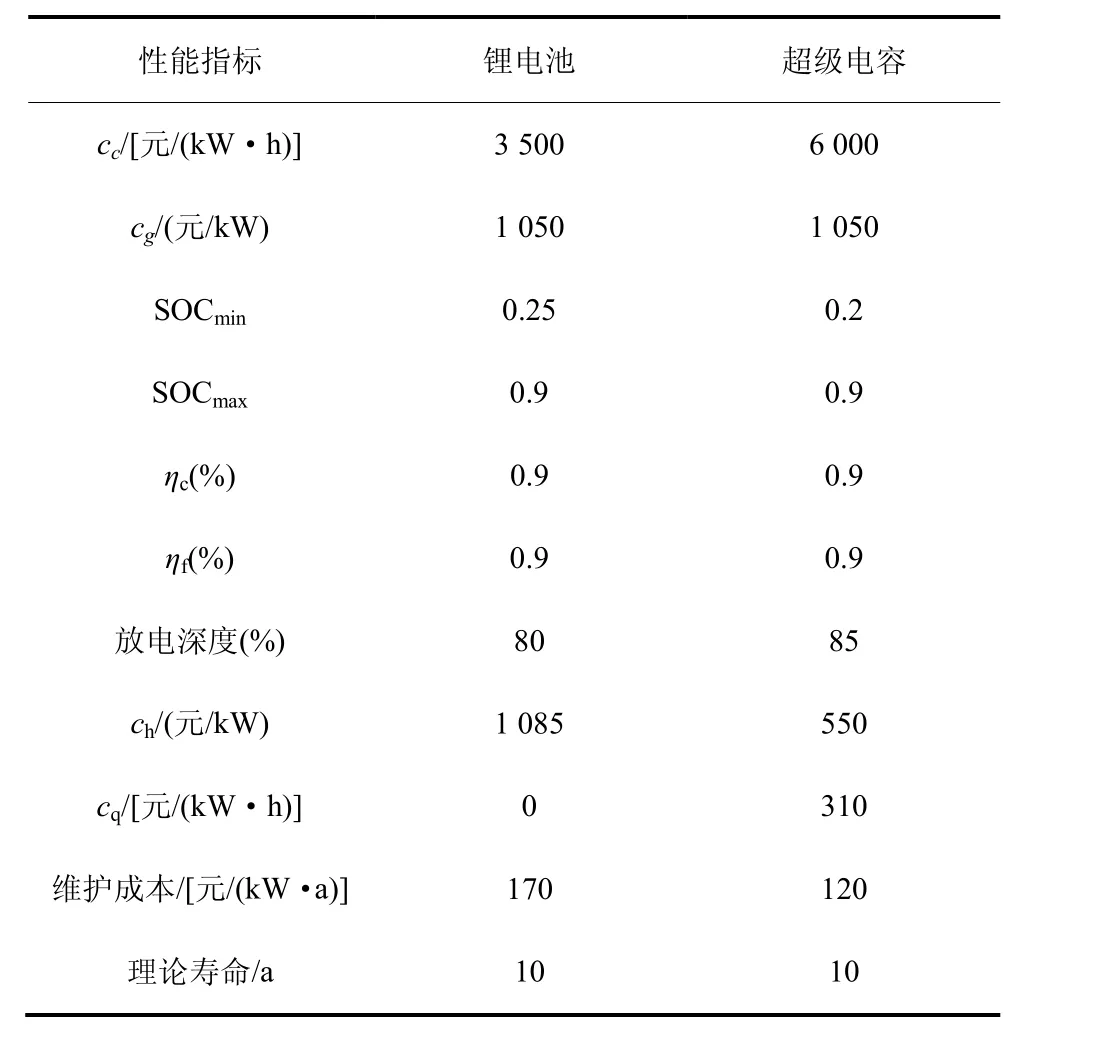
表2 电池参数

在考虑分时电价情况下，满足最大负荷时储能的容量需如图8 所示。

光伏装机容量为181 kW，考虑变换器的效率(ηd=0.95，η=0.84)以及5%的裕量后，优化后的结果如图8 所示，电网供电时间段为0～8 h，储能充电时间为6～16.3 h，放电时间为16.3～24 h。

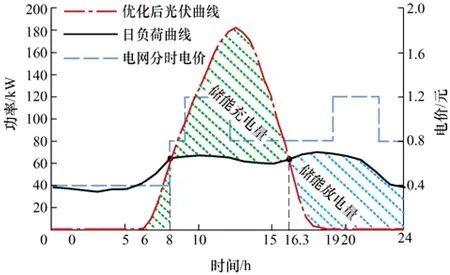
图8 优化光储示意图

确定储能容量后，根据运行成本模型可得到微电网的运行成本。其次，利用优化算法求解模型，获得成本最低时混合储能成本和各自容量配比，以IPMOCSA 为例，如图9 所示为其求解的一组Pareto解。

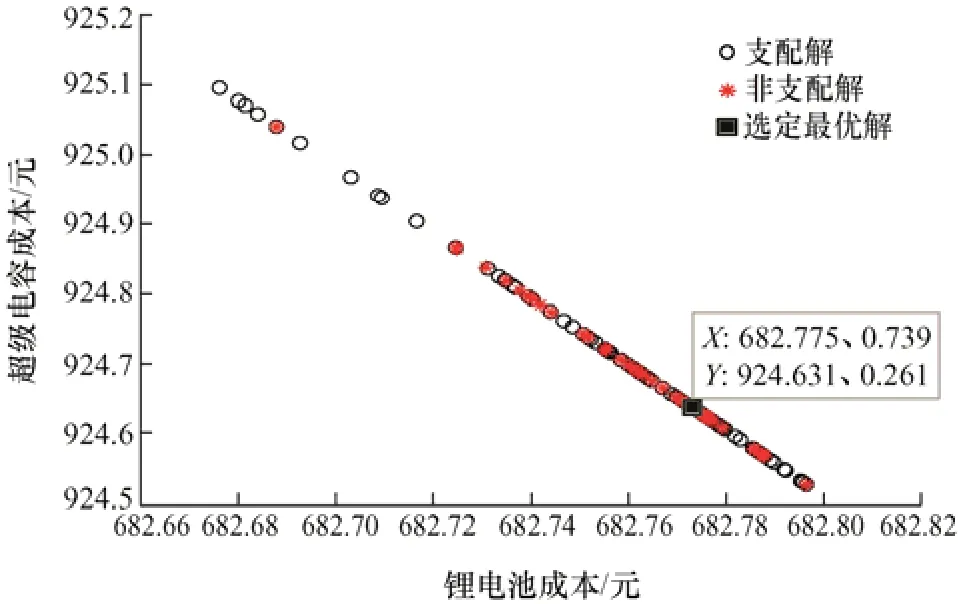
图9 IPMOCSA 的一组Pareto 解

图10 中分别是利用MOPSO 和IPMOCSA 进行20 次求解所配置的容量占比，本次寻优两者迭代次数都为100 次，种群数量为100，配置目标分别为超级电容和锂电池的日均成本，以及各自所占比重，可以看出改进乌鸦搜索算法进行20 次求解所得结果比粒子群算法的收敛性强，由图10 可知IPMOCSA20次的求解结果大多数收敛区域在0.2～0.35 之间，通过对此区域点加权求平均值后，粒子群算法中锂电池占比为0.294，改进乌鸦搜索算法中锂电池占比为0.261，则配置结果如表3 所示。

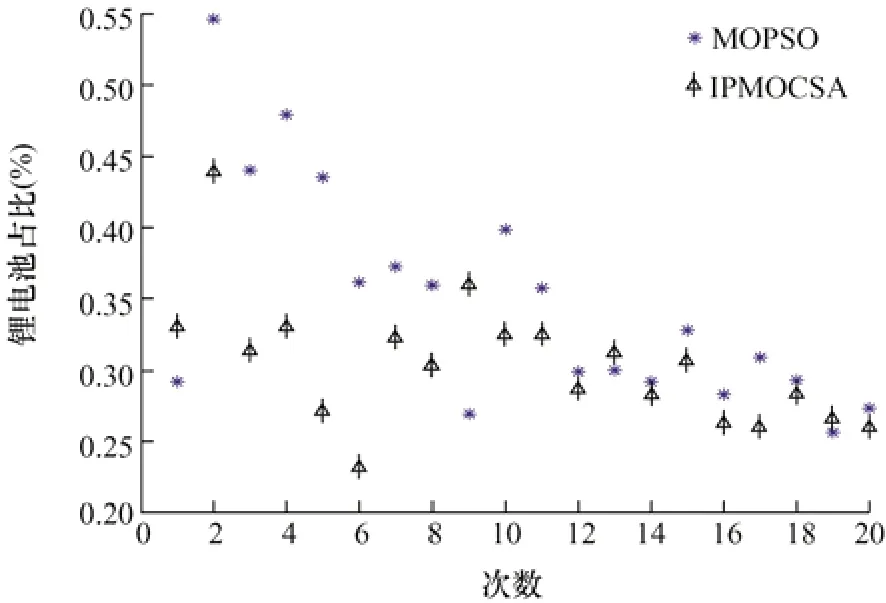
图10 混合储能容量配置

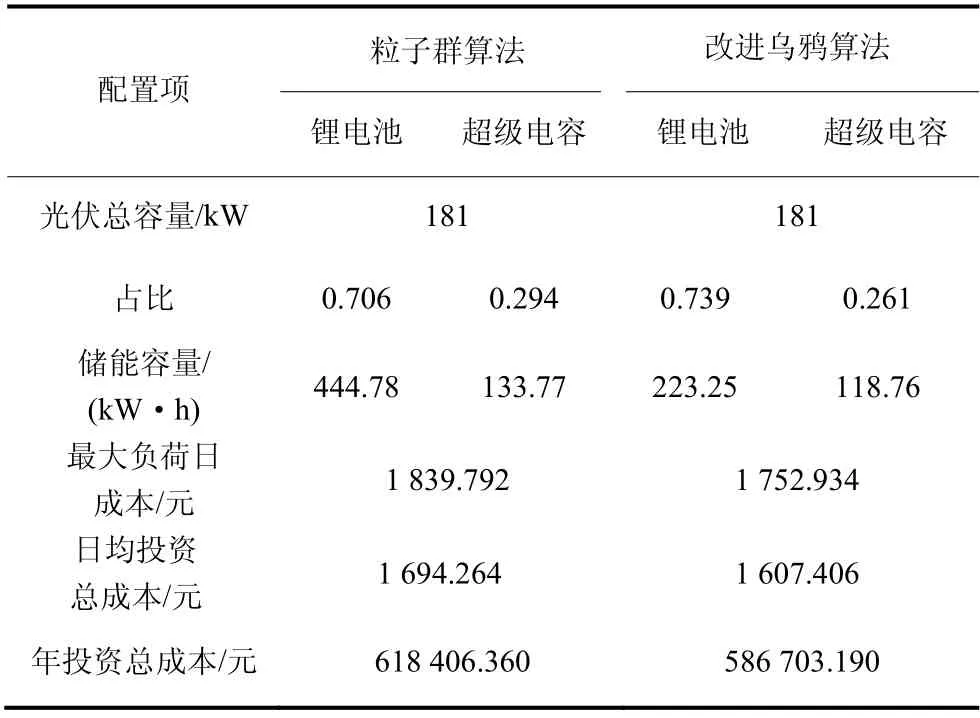
表3 混合储能配置结果

根据图10 及表3 可知，在储能容量及负荷相同时，IPMOCSA 结果比MOPSO 寻优结果更加理想。针对本文算例 MOPSO 计算的日均成本比IPMOCSA 的日均成本高了86.858 元，综合整体项目投资年限为20 年，混合储能的投资成本多出634 063.4 元，占比5.13%，证明本文所提方法的有效性。

6 结论

本文针对光伏微网中混合储能的容量优化配置问题，以经济性为目标建立系统的双层优化模型，并提出一种IPMOCSA 进行求解，获得最优化配置结果。

(1) 考虑投资成本及微电网的运行成本建立目标函数。在运行成本模型建立过程中，计及电网分时电价影响，提出微电网和储能的运行策略，并据此配置储能最小容量。

(2) 在CSA 中引入粒子群算法向全局最优趋近的思想，改善了乌鸦算法的盲目性；其次，为增加算法的多样性，避免算法陷入局部最优，将莱维飞行的思想引入乌鸦飞行步长，并将此用于混合储能容量优化配置。

(3) 为证明改进算法的有效性，通过将某地一商业楼2019 年用电负荷作为容量优化配置的依据，对比IPMOCSA 及MOPSO 在混合储能容量优化配置的结果，结果表明改进算法配置的容量可节约成本5.13%。