基于分层优化的电动汽车有序充电策略*

冯仕杰 刘 韬 潘 萨,3 陈正浩 王 青

(1. 南昌大学信息工程学院 南昌 330031；2. 国网江西省电力有限公司景德镇供电分公司 景德镇 333000；3. 国网重庆市电力有限公司万州供电公司 重庆 404155)

1 引言

电动汽车作为一种新能源汽车，具有高效、清洁的特点，在缓解能源短缺、减轻环境污染等方面具有较大的优势，目前已成为世界各国的战略发展目标，我国“十二五”规划明确指出将电动汽车行业作为未来战略发展目标，预计在2030 年每年生产1 500 万辆电动汽车[1]。

大规模的电动汽车充电会给配电网的安全运行带来挑战，若不进行适当的调控，配电网负荷波动将会加剧，并带来设备过载、电压功率因数下降等不良影响[2-3]。

为了保证配电网的安全运行，减小电动汽车无序充电带来的影响，国内外学者开展了电动汽车充电优化策略的研究。目前电动汽车的充电优化策略主要分为集中式充电优化方式和分层充电优化方式两种。其中，集中式充电优化方式是根据建立的充电优化模型对当前时段接入的所有电动汽车进行集中式优化，这个过程通常由控制中心独立完成。文献[4-5]提出了以配电网网损最小为目标的充电优化方法；文献[6]针对配电网的负荷波动，将配电网高峰时段的充电负荷转移至夜间低谷期，减少了配电网的负荷峰谷差；文献[7-8]以电网购电成本最小为目标，优化电动汽车的最优充放电时段。上述文献都是通过集中式充电优化的方法来调控电动汽车的充电时段，但这种优化方式的计算量较大，通常需要大量的信息传递，不利于电动汽车充电的实时优化。

针对电动汽车集中式充电优化方式计算量大、通信要求高的问题，相关文献开展了电动汽车分层充电优化方式的研究。在分层充电优化方式中，代理商起到连接电动汽车与控制中心的作用，控制信号先由控制中心发送至本地代理商，再由代理商将信号分发至每辆电动汽车，这种控制方式降低了通信难度，更适用于电动汽车的实时调度。文献[9]提出一种由代理商分散控制的充电管理方式，代理商负责计算区域内电动汽车的充电负荷曲线，控制中心再对各区域的电动汽车进行协调控制；文献[10]针对配电网负荷波动，提出了上层以减少负荷波动为目标、下层以上下层调度偏差最小为目标的双层优化模型。上述文献考虑了配电网的利益，但忽略了用户的充电成本，且认为所有的用户均愿意服从充电安排。

文献[11]建立了双层充电优化模型，上层模型以全局利益为目标，为下层模型提供约束条件，下层模型以各节点充电费用和充电偏差最小为目标，将各节点对上层控制所得功率指导结果为约束条件，采用交替方向乘子法求解目标函数，各个节点之间不断协调合作，从而得到单个电动汽车充电时段的最优解，该方法需要大量的信息传递，因此对通信的要求较高；文献[12]引入分层分区的理念，上层采用粒子群算法优化各时段的总充放电功率，下层采用顺序选择法保障用户的充电满意度，粒子群算法在处理大规模的优化问题时容易受到种群多样性的影响，出现陷入局部最优的情况，导致优化效果较差。

针对上述问题，本文以电动汽车的充电时段为优化目标，建立了包含用户充电费用最少、配电网总负荷方差最小的电动汽车分层优化模型。上层以充电费用最少为目标，根据车辆在电价低谷时段充电时间越久充电费用越少的准则优化车辆的充电时段范围，从而得到满足充电费用最少的全部最优解，并将其作为下层优化的约束条件，减轻了下层充电优化的计算负担；下层以配电网总负荷方差最小为目标通过改进的粒子群算法求解优化模型，提高了粒子群算法的优化效果。结合算例，利用所提出的模型，对比分析了不同充电数量、不同用户响应度下配电网负荷、用户充电费用的优化结果。

2 电动汽车分层充电优化策略

电动汽车的分层充电优化策略主要由智能充电桩和本地运营商两部分组成，针对用户充电成本，智能充电桩以用户充电费用最少为目标选取电动汽车的充电时间范围，针对配电网负荷波动，本地运营商以配电网总负荷方差最小为目标优化电动汽车的充电起始时间。

2.1 电动汽车的充电时长计算

为了确保电动汽车在充电后的荷电状态(State of charge，SOC)达到用户设置的期望值SOCe，需要计算电动汽车的充电时长Tc，计算公式如式(1)所示

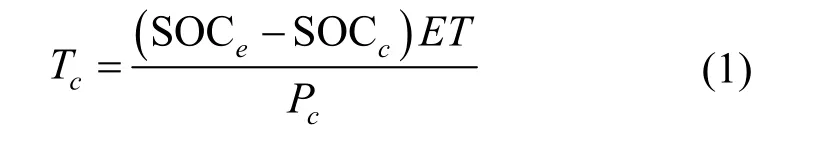
式中，SOCc为电动汽车接入充电桩时的荷电状态，ET为车辆的蓄电池容量，Pc为充电功率。

2.2 电动汽车充电分层优化模型

考虑到电动汽车接入、离开充电桩的时间具有很大的随机性，本文将一天分为96 个时段，对电动汽车充电进行分时段优化。

2.2.1 智能充电桩优化模型

电动汽车在充电开始前用户有权选择充电过程是否服从电网安排，对于电动汽车用户来说，充电成本是用户选择服从电网安排的主要因素，因此智能充电桩以用户充电费用最少为目标，目标函数如式(2)所示

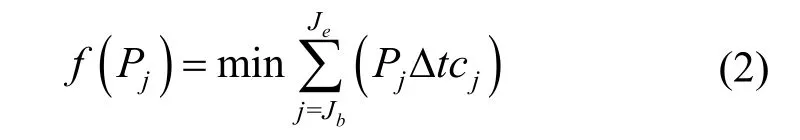
式中，Jb为车辆接入充电桩的时段；Je为用户设置的离开充电桩时段；Pj为电动汽车在时段j的充电功率(若车辆在时段j充电，则Pj等于Pc，若车辆不在时段j充电，则Pj等于0)；Δt为每个时段时长，取0.25 h；cj为第j个时段的电动汽车充电电价。

电动汽车在充电结束后的电池容量应满足式(3)所示的约束条件

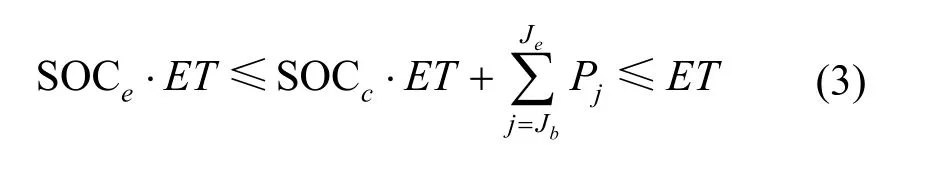
2.2.2 本地运营商优化模型

考虑到电动汽车充电对电网负荷波动的影响，本地运营商以配电网总负荷方差最小为目标，目标函数如式(4)所示

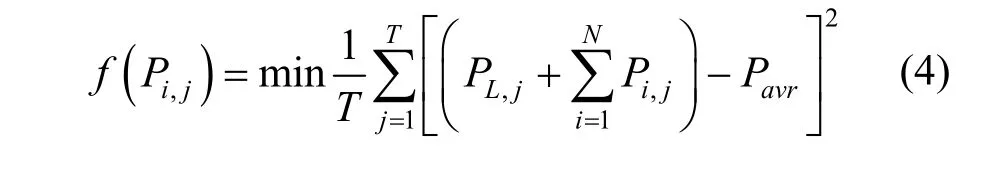
式中，T为一天时段段数，取96；N为第j个时段内接入充电桩的电动汽车总量；PL,j为第j个时段的配电网常规负荷；Pi,j为车辆i在时段j的充电功率；Pavr为优化时段内配电网总负荷的平均值，如式(5)所示。

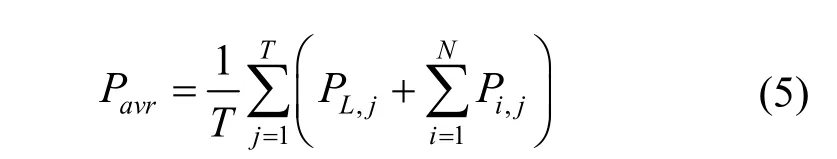
假设智能充电桩根据优化模型求得的车辆充电时段范围为[Jcb,i，Jce,i]，则电动汽车的充电时段需要满足式(6)所示的约束条件，除此之外，每辆电动汽车的电池容量也应满足式(3)所示的约束条件。

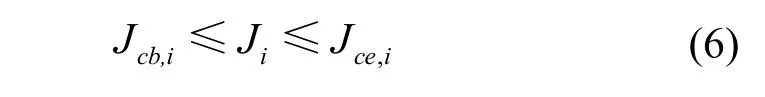
式中，Ji为车辆i的充电时段。

2.3 电动汽车充电分层优化控制流程

电动汽车充电分层优化控制流程如图1 所示，步骤如下。

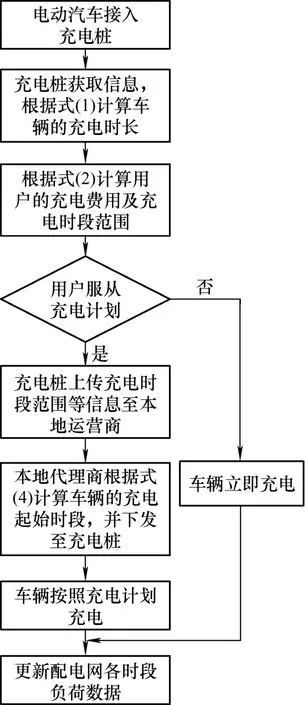
图1 电动汽车充电分层优化控制流程图

(1) 电动汽车接入智能充电桩后，充电桩获取车辆的电池状态、用户设置的离开充电桩时间、充电结束时期望车辆达到的SOC 等信息，并根据式(1)计算车辆的充电时长。

(2) 充电桩根据式(2)求解满足用户充电费用最少的充电时段范围及充电费用，并将充电时段范围及充电费用传递给用户。

(3) 用户根据充电时间范围及充电费用选择是否服从充电计划，若不服从则充电立即开始，充电桩将充电时间上传至本地运营商，本地运营商更新配电网各时段的负荷数据，若服从充电计划则充电桩将车辆的充电时间范围、电池状态、用户设置的信息上传至本地运营商。

(4) 本地运营商根据式(4)优化电动汽车的充电起始时段，并将优化后的充电起始时段下发至充电桩。

(5) 充电桩根据车辆的充电起始时间执行充电计划，本地运营商更新配电网各时段的负荷数据。

3 智能充电桩优化模型求解

智能充电桩以用户充电费用最少为目标，其优化模型通常具有多个最优解，因此能够在用户充电费用最小化的基础上进一步以配电网负荷方差最小为目标进行分层优化。

常用的优化模型求解方法一般分为智能优化算法和穷举法，其中智能优化算法具有较高的计算效率，能够较好地处理复杂的优化问题，但所得的最优解通常只有一个，若要实现本文提出的分层优化策略，则需要将智能充电桩求得的最少充电费用作为本地运营商优化的约束条件，使本地运营商优化后的用户充电费用不大于智能充电桩求得的最少充电费用，这样虽然能够保障用户的利益，但是会加大本地运营商的计算量，不利于电动汽车充电的实时优化。

穷举法根据搜索空间列出所有可行解，能够得到满足条件的全部最优解，但计算较为复杂，对设备的硬件要求较高，针对以上问题，本文转变求解思路，将计算用户充电费用最少的问题转变为计算车辆在电价谷时段充电时长最久的问题。

根据充电分时电价可知若车辆在电价最低时段充电时间越久则充电费用越少，因此将充电时段分情况考虑，假设充电电价谷时段为[Jlb，Jle]，车辆接入充电桩时段为Jb、离开充电桩时段为Je，充电时长为Jc，分析车辆所有可能的停留时段与电价谷时段的关系，当满足以下条件时，最优充电时段范围如下所示。

(1) 当Jb＜Jlb，Je＜Jle，Jlb+Jc＜Je时，车辆能够全程在电价谷时段充电，此时最优充电时段范围为[Jlb，Je]。

(2) 当Jb＜Jlb，Je＜Jle，Jlb+Jc≥Je时，车辆在谷时段最多充(Je－Jlb)个时长，此时最优充电时段范围为[Jε－Jc，Je]。

(3) 当Jb＜Jlb，Je≥Jle，Jlb+Jc＜Jle时，车辆能够全程在电价谷时段充电，此时最优充电时段范围为[Jlb，Jle]。

(4) 当Jb＜Jlb，Je≥Jle，Jle≤Jlb+Jc＜Je，Jb+Jc＜Jle时，车辆在谷时段最多充(Jle－Jlb)个时长，此时最优充电时段范围为[Jle－Jc，Jlb+Jc]。

(5) 当Jb＜Jlb，Je≥Jle，Jle≤Jlb+Jc＜Je，Jb+Jc≥Jle时，车辆在谷时段最多充(Jle－Jlb)个时长，此时最优充电时段范围为[Jb，Jlb+Jc]。

(6) 当Jb＜Jlb，Je≥Jle，Je≤Jlb+Jc，Jb+Jc＜Jle时，车辆在谷时段最多充(Jle－Jlb)个时长，此时最优充电时段范围为[Jle－Jc，Je]。

(7) 当Jb＜Jlb，Je≥Jle，Je≤Jlb+Jc，Jb+Jc≥Jle时，车辆在谷时段最多充(Jle－Jlb)个时长，此时最优充电时段范围为[Jb，Je]。

(8) 当Jb≥Jlb，Je＜Jle时，车辆能够全程在电价谷时段充电，此时最优充电时段范围为[Jb，Je]。

(9) 当Jb≥Jlb，Je≥Jle，Jb+Jc＜Jle时，车辆能够全程在电价谷时段充电，此时最优充电时段范围为[Jb，Jle－Jc]。

(10) 当Jb≥Jlb，Je≥Jle，Jb+Jc≥Jle时，车辆在谷时段最多充(Jle－Jb)个时长，此时最优充电时段范围为[Jb，Jb+Jc]。

该方法计算简单，对设备的硬件要求较低，得到的最优充电时段范围保留了满足用户充电费用最少的所有最优解，将最优充电时段范围作为本地运营商优化的约束条件，能够减少本地运营商优化的计算量。

4 基于改进粒子群算法的本地运营商优化模型求解

4.1 粒子群算法

粒子群算法主要模拟了鸟群寻找食物的过程，在鸟群搜寻过程中，每只鸟知道食物离自己的距离，但不知道食物的具体位置，为了获得食物，鸟儿们会共享自己的位置信息，找出离食物最近的鸟儿位置，并向着那个位置靠近，整个过程中鸟群会在离食物最近的位置周围搜索，直到找到食物。优化过程中，粒子的更新方式如式(7)所示

4.2 改进粒子群算法

4.2.1 基于Tent 混沌映射的粒子种群初始化混沌映射具有较好的遍历性，常被用于解决算法的搜索问题，常用的混沌模型主要有Logistic 模型和Cubic 模型，相关研究表明Tent 混沌映射比Logistic 混沌映射具有更好的混沌特性[13]，因此本文将Tent 混沌映射引入到种群的初始化上，用混沌映射生成的序列替代rand()随机数。Tent 混沌映射模型如式(11)所示

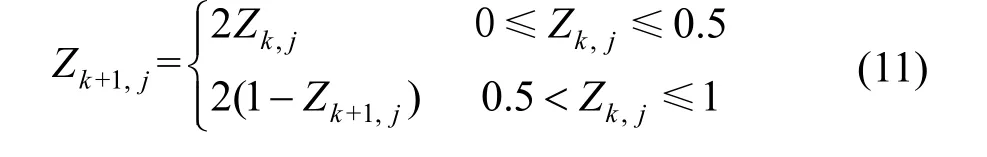
式中，k为迭代次数，k=0, 1, 2, …,N；Zk+1，j为第k+1次迭代后映射在j维上的混沌变量，当k=0 时，Z0,j为[0, 1]之间的随机数。

Tent 映射的序列中存在着不动点与周期循环点，若Zk,j为0、0.25、0.5、0.75，序列将迭代为0，若Zk,j=Zk+m,j(m={1, 2, 3, 4})，序列最终将陷入周期循环。为此当出现以上情况时，Tent 混沌映射模型更改为式(12)的形式

式中，Vmax,j、Vmin,j分别为粒子在j维的最大、最小速度。

4.2.2 动态调整速度权重

粒子群算法的搜索过程主要取决于粒子速度的大小，为了提高算法前期的全局搜索能力、加快算法后期的收敛速度，将速度更新中的权重w调整为随迭代次数变化的动态值，使得w在算法前期较大，有利于算法的全局搜索，在算法后期较小，提高算法的收敛速度。w的计算公式如式(15)所示

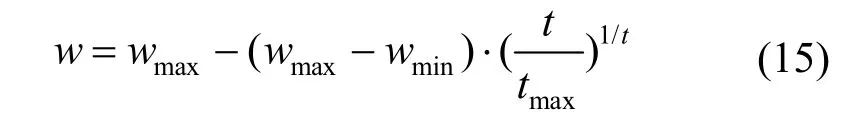
式中，tmax为最大迭代次数。

4.2.3 基于Levy 飞行的扰动策略

Levy 飞行因其独特的移动方式在算法优化上得到了大量的应用，其步长服从莱维分布，在搜索路径上具有短距离飞行与偶尔长距离飞行的特点，研究表明Levy 飞行能够帮助种群扩大搜索范围，提高算法的优化性能[14-15]，Levy 飞行的简单数学模型如式(16)所示

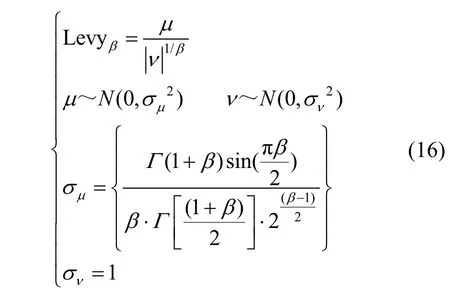
式中，Levyβ为Levy 飞行的随机步长，β为常数，一般设为1.5；Γ是伽马函数。

为了进一步增强算法的寻优能力，本文将Levy飞行机制引入到粒子的位置更新中。在每次迭代结束后利用Levy 飞行步长扰动粒子位置，扰动后的粒子位置如式(17)所示

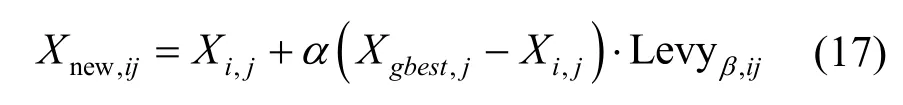
式中，α为步长控制参数。

Levy 飞行扰动可以增加粒子种群的多样性，但可能导致扰动后粒子的适应度变差，为此引入贪婪策略，将扰动后粒子的适应度f(Xnew,i)与原来位置的适应度f(Xi)进行比较，选取适应度较好的位置，如式(18)所示

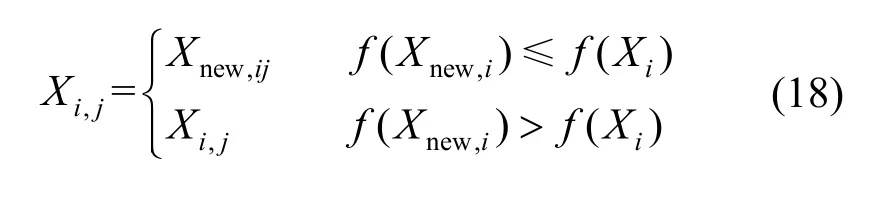
4.3 改进粒子群算法的优化流程

通过改进的粒子群算法求解本地运营商优化模型，步骤如下所示。

(1) 设置算法参数，根据式(13)、式(14)初始化粒子的位置、速度。

(2) 根据式(4)计算每个粒子的适应度，记录每个粒子历史适应度最好的位置与种群中全局适应度最好的位置。

(3) 根据式(7)、式(8)更新粒子位置、速度。

(4) 根据式(17)对粒子进行扰动，并根据式(18)决定粒子是否更新位置。

(5) 若循环次数达到最大迭代次数则输出最优解，若不满足则返回步骤(2)。

5 仿真结果分析

5.1 算例描述

本文的仿真试验在Windows10PC 机(2.6 GHZ，4 GB，双核CPU)，Matlab R2014b 版本上进行，参数设置如下。

电动汽车的电池容量在20～40 kW·h 均匀分布，充电功率为3 kW，用户的期望SOC 均为1，电动汽车接入充电桩时间To、预计离开充电桩时间Tg满足正态分布[15]，To～N(17.47,3.412)，Tg～N(8.92,3.242)；日行驶里程D满足对数正态分布[16]，ln(D)～N(2.98，1.14)。

改进粒子群算法的种群数量为30，最大迭代次数tmax为200，速度权重最大值Wmax设为0.9、最小值Wmin设为0.3，学习因子c1、c2设为2。

图2 为某区域配电网常规负荷曲线，11 点和19点左右有两个负荷高峰，负荷最大值为2 932 kW。

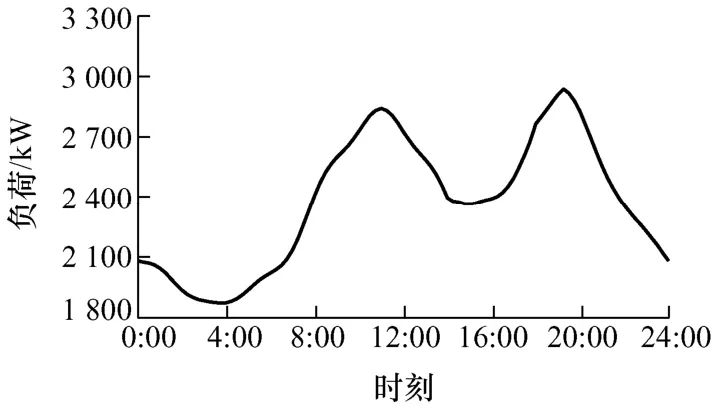
图2 区域配电网常规负荷曲线

电动汽车充电电价采用峰谷电价[17]，如表1所示。

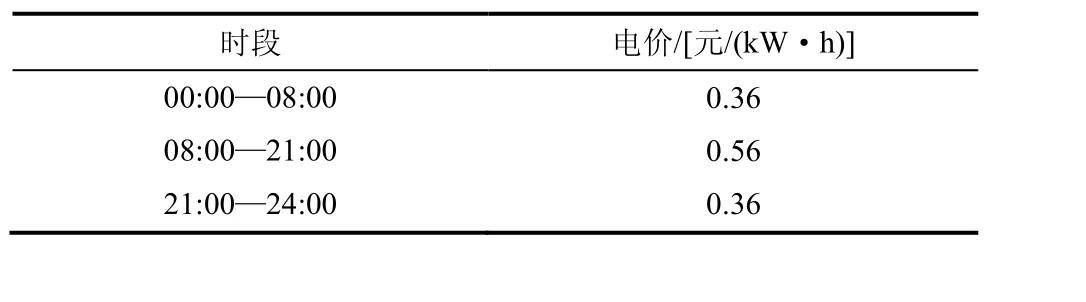
表1 充电峰谷电价

5.2 仿真结果与分析

5.2.1 用户响应度对优化结果的影响用户在车辆充电前根据充电桩提供的充电时间范围及充电费用选择是否服从充电计划，若用户不服从，则充电立即开始。由于用户的主观意愿不能掌控，在进行电动汽车充电负荷模拟仿真时，有必要引入用户对充电计划的响应度r(服从充电安排的用户人数占所有用户的比例)来分析不同响应度下的电动汽车优化情况。当r=0%时(电动汽车无序充电)，车辆接入充电桩后立即充电，采用蒙特卡洛法根据To、Tg、D的概率密度分布随机生成用户信息，以接入充电桩时段Jb为充电起始时段，根据式(19)计算得到r=0%时时段j的车辆充电负荷Ps,j。

当300 辆电动汽车接入充电桩后，用户不同响应度下的配电网总负荷曲线如图3 所示。

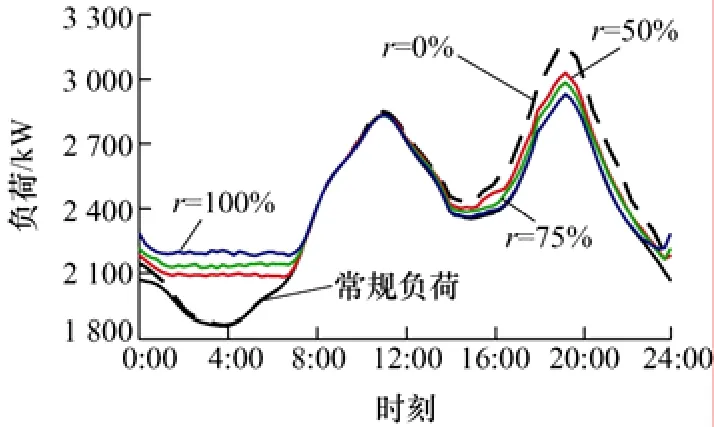
图3 用户不同响应度下的配电网负荷曲线

从图3 可以看出当r=0%时，电动汽车主要集中在17:00—22:00 充电，导致配电网的峰值负荷进一步增大，负荷波动更加剧烈；当r=50%时，17:00—22:00 的配电网总负荷明显下降，电动汽车充电负荷开始转移到00:00—08:00 时段；当r=100%时，电动汽车充电负荷的转移效果较好，负荷峰值明显降低，负荷曲线更加平稳。

表2 为不同用户响应度下的优化结果，可以看出当r从0%到100%时，配电网负荷峰谷差降低了42.3%，负荷方差下降了59.7%，用户总充电费用下降了27.5%。

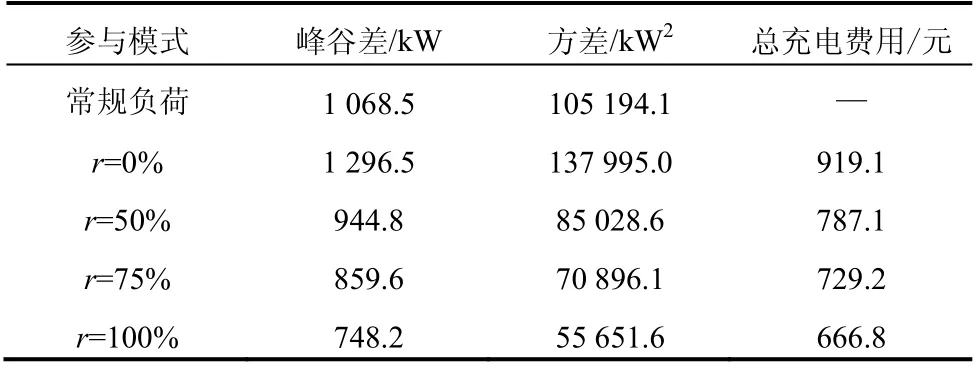
表2 不同用户响应度下优化结果的对比

5.2.2 充电数量对优化结果的影响

在实际系统中，大多数人会服从充电计划以便减少自身的充电费用，但部分人可能急需用车，需要车辆更早地结束充电，为此将用户响应度定为75%，分析该响应度下不同充电数量对优化结果的影响，当200 辆、300 辆、400 辆电动汽车接入充电桩后，不同充电数量下的配电网总负荷曲线如图4 所示。

图4 不同充电数量下的配电网负荷曲线

从图4 可以看出，随着优化车辆的增加，配电网峰值、谷值负荷逐渐变大，但峰值负荷增大幅度较小，因此负荷曲线将会更加平稳。

表3 为不同充电数量下的优化结果，可以看出随着充电数量的增大，配电网负荷峰谷差、方差逐渐减小，说明车辆的充电数量越多，本文所提策略的优化效果越好。

表3 不同充电数量下优化结果的对比

为了体现本文算法改进的有效性，将改进后的粒子群算法(CPSO)与原始粒子群算法(PSO)比较，PSO 的种群数量、迭代次数、学习因子与CPSO 设置一致，权重设为0.6，将PSO 算法用在200、300、400 辆电动汽车的充电优化中，用户响应度设为75%，各算法的收敛曲线如图5 所示。

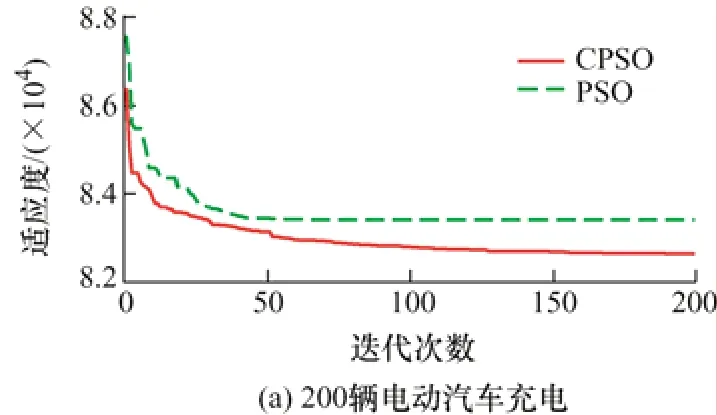
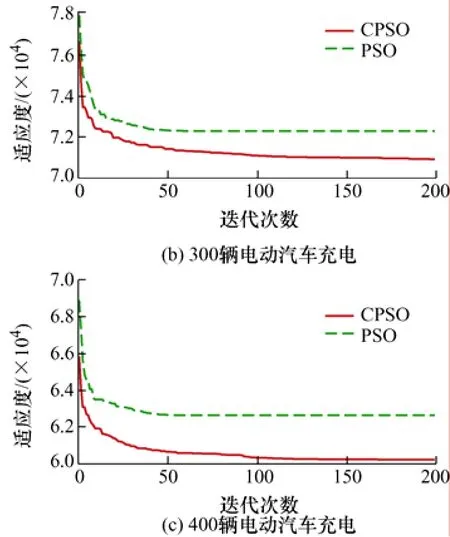
图5 两种算法的收敛曲线

从图5 可以看出改进PSO 算法能够有效提升算法的精度，随着充电数量的增加，CPSO 算法的全局搜索能力越强，能够有效地跳出局部最优解，更有利于电动汽车的充电优化。

6 结论

本文分析了电动汽车不同充电情况下对电网负荷波动的影响，建立了考虑用户充电费用、配电网总负荷方差的电动汽车充电分层优化模型，利用改进的粒子群算法对目标进行了优化，由仿真结果得到如下结论。

(1) 随着用户响应度、充电数量的增大，电动汽车充电的优化效果越好，优化后的车辆充电时段大都分布在配电网负荷低谷期，有效地减小了配电网的负荷波动以及用户充电成本。

(2) 改进的粒子群算法具有较好的全局搜索能力，能够有效地提高算法的收敛精度，相较于原始粒子群算法，改进粒子群算法能够较好地解决电动汽车的充电优化问题。