质子交换膜燃料电池膜电极组件温度分布的神经网络预测模型

李志浩，彭 浩，陈亚琴

（上海海事大学航运仿真技术教育部工程研究中心，上海 201306）

燃料电池膜电极组件温度分布会影响燃料电池的性能[1]，进而影响电池的工作效率[2-3]。质子交换膜燃料电池膜电极组件的温度分布会影响电池内部水分布[4]。温度分布引起的电极膜组件局部脱水或水凝结会导致电池性能下降[5]。同时，质子交换膜燃料电池膜电极组件的温度分布会影响燃料电池的寿命和可靠性。质子交换膜燃料电池温度控制需要电池热管理系统来实现，热管理系统的设计需要以质子交换膜燃料电池膜电极组件的温度分布为依据。因此，确定质子交换膜燃料电池内部膜电极组件表面的温度场对提高电池工作效率和延长电池工作寿命很重要。故有必要对质子交换膜燃料电池的温度分布进行预测。

现阶段质子交换膜燃料电池温度分布预测模型较少。在已有的质子交换膜燃料电池温度分布模型中，大部分为数值模拟和经验模型[6]。高一方等[7]利用傅里叶拟合的经验模型，研究了质子交换膜燃料电池温度与电压、电流密度的关系，结果表明运用3 次傅里叶拟合模型控制温度最佳。马天才等[8]人提出了一种质子交换膜燃料电池的热力系统动态数学模型，研究燃料电池电化学反应的热力学特性，结果表明该模型简化了燃料电池设计相关参数计算的过程。Choi 等[9]建立了质子交换膜燃料电池的数值仿真模型，研究了不同冷却方式下内部质子交换膜燃料电池内部的温度分布，结果表明两相HFE-7100 冷却法在温度保持和温度均匀性方面具有优势。在他人的研究中，多是对燃料电池平均温度进行的预测，很少考虑到燃料电池温度分布的问题。同时，文献中对燃料电池温度的研究没有充分考虑到燃料电池温度的不确定性与非线性,并且未充分利用试验中获得的大量实测数据。故本文希望提出一种模型来精确预测质子交换膜燃料电池的阳极电极组件的温度分布情况。

神经网络模型可以学习和构建非线性的具有复杂关系的模型。并且神经网络模型具有推广性，在学习已有数据之后，它可以推断出未知数据之间的关系，从而使得模型能够预测未知数据。本文提出了一种预测质子交换膜燃料电池工作状态下温度分布的人工神经网络模型，利用径向基函数(Radial Basis Function，RBF)、广义回归(Generalized Regression Neural Network，GRNN)神经网络学习已有数据，并预测了在不同工况下膜电极组件表面的温度分布。

1 人工神经网络模型的建立

1.1 样本数据的获得

针对质子交换膜燃料电池膜电极组件表面的温度，本文使用了郭航等人之前发表的数据[5-6]，作为建立人工神经网络预测模型的样本数据。数据来源与工况具体如表1所示。

表1 样本数据来源和工况Table 1 Sample data source and condition

燃料电池采用平行流道与蛇形流道结构，通道宽度均为3 mm、肋宽1.5 mm、流道深度为2.5 mm。其燃料电池反应活性区域尺寸为29 mm×39 mm。实验可视化温度场中获取的温度点位置如图1、图2所示。在图1 中，燃料从左上方流入进入反应区域，数字1～27代表测温点的相对位置，反应残余物从右下角的位置排出燃料电池。在图2中，燃料从左上方流入进入反应区域，数字1～27代表测温点的相对位置，反应残余物从右下角的位置排出燃料电池。

图1 平行流道质子交换膜燃料电池可视化温度场中的温度点位置[6]Fig.1 The temperature point position obtained in the visualized temperature field of the measured parallel flow channel proton exchange membrane fuel cell[6]

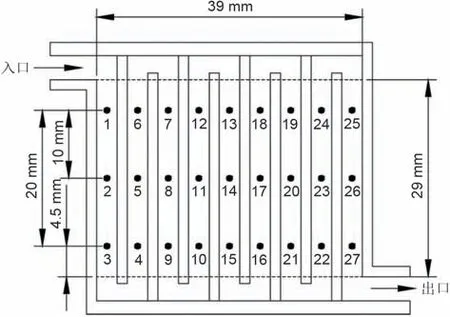
图2 蛇形流道质子交换膜燃料电池可视化温度场中的温度点位置[7]Fig.2 The temperature point position obtained in the visualized temperature field of the measured snake flow channel proton exchange membrane fuel cell[7]

1.2 RBF人工神经网络模型

由于RBF 神经网络具有较强的非线性拟合能力，而且学习规则简单，便于计算机实现。所以本文采用了具有输入层、隐含层、输出层三层结构的RBF神经网络，如图3所示。输入层包含108个输入节点，每个输入节点包含两个参数，分别为电流密度与温度点的位置。选取电流密度与温度点的位置作为输入参数的原因主要有以下两点。①已有研究表明，建立温度模型需要电压与电流密度两个参数[7]，建立温度分布模型选取点位的位置、电压和电流密度3个参数即可。在本文选用的数据中，燃料电池的燃料流速恒定，电流密度与电压具有一定的函数关系，当电流密度确定时，电压便唯一确定，则本模型可以用两个参数来代表三个参数作为模型输入；②选用更精简的输入可以简化模型使神经网络模型更快速地拟合。

图3 RBF人工神经网络的结构。输入层为预测影响因素，输出层为预测的温度分布。隐含层具有很多的神经元Fig.3 Structure of RBF Artificial Neural Network.The input layer is the predicted influencing factors,and the output layer is the predicted temperature distribution.The hidden layer has a lot of neurons

RBF神经网络模型有且仅有一层隐含层，通过径向基函数将输入样本映射到隐含层上。隐含层的神经单元节点数等于输入节点数，在本模型中为108个。

在RBF 神经网络模型中，径向基函数节点构成了隐含层的变换函数，本文模型中使用高斯核函数作为径向基函数[12]，形式如下：

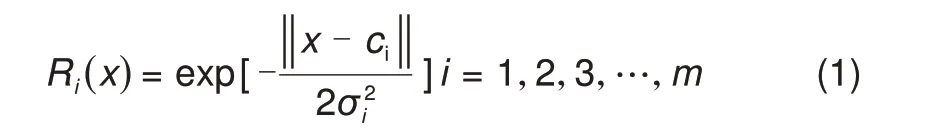
其中，x是n维输入向量；ci是第i个径向基函数的中心点的参数，两个向量具有一样的纬度；σi是输入向量到径向基函数中心点的距离；m是神经元结点的个数。‖‖x-ci为径向基函数的自变量，表示x与ci之间的间隔，Ri(x)有且只有一个最大值在ci处，随‖x-ci‖的变大，Ri(x)快速的减小为0.

质子交换膜燃料电池温度数据集包含135个样本，它们被分成80%的训练集和20%的验证集。

表2 RBF神经网络模型的基本参数Table 2 Basic parameters of RBF neural network model

1.3 GRNN人工神经网络模型

作为RBF 神经网络的改进网络，一般情况下GRNN神经网络具有更好的非线性映射能力和学习速度。所以本文采用了具有输入层、模式层、求和层、输出层四层结构的GRNN神经网络[13]作为RBF神经网络模型的对照，如图4 所示。输入层包含108个输入节点，每个输入节点包含两个参数，分别为电流密度与位置。模型包括模式层与求和层两个隐含层，数据通过径向基函数映射到模式层，再加权求和得到温度分布结果。

图4 GRNN人工神经网络的结构。输入层为预测影响因素，输出层为预测的温度分布Fig.4 Structure of GRNN artificial neural network.The input layer is the predicted influencing factors,and the output layer is the predicted temperature distribution

在GRNN神经网络模型中，模式层传递函数为径向基函数，这里仍然使用高斯核函数[14]，形式见式(2)

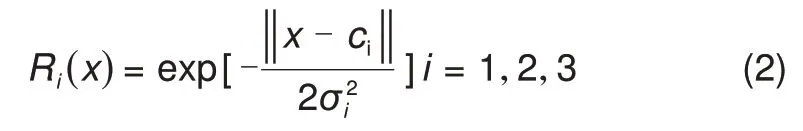
分子神经元求和[14]：

1.4 神经网络模型的精度评价

使用测试数据集来确定模型的性能。为了评估人工神经网络模型的性能，我们使用了决定系数(coefficient of determination，R2)、均方根误差(root mean square error，RMSE)、平均绝对百分误差(mean absolute percent error，MAPE)[15]，定义如下

表3 GRNN神经网络模型的基本参数Table 3 Basic parameters of GRNN neural network model

2 人工神经网络模型结果

2.1 神经网络模型的选择

图5(a)～(c)分别显示了RBF 神经网络模型的均方根误差、平均绝对百分误差和决定系数随扩展速度的变化情况。图5(a)表示了均方根误差随扩展速度的变化。对测试集1，均方根误差随扩展速度的上升稳定下降，在0.6之后达到最小值0.1左右。对测试集2，均方根误差在扩展速度为0.7 时取得最小，然后随着扩展速度的增大出现波动。图5(b)表示了平均绝对百分比误差随扩展速度的变化。与均方根误差随扩展速度的变化相似，对测试集1，平均绝对百分比误差随展张速度的上升稳定下降，在0.6之后达到最小值1%左右。对测试集2，平均绝对百分比误差在扩展速度为0.7 时取得最小，然后随着扩展素的增大出现波动。图5(c)表示了决定系数随扩展速度的变化。对测试集1，决定系数随扩展速度的增大稳步上升，在扩展速度达到0.5时，达到0.95左右，随后趋于平稳。对测试集2，决定系数较为稳定，一直维持在0.9左右。

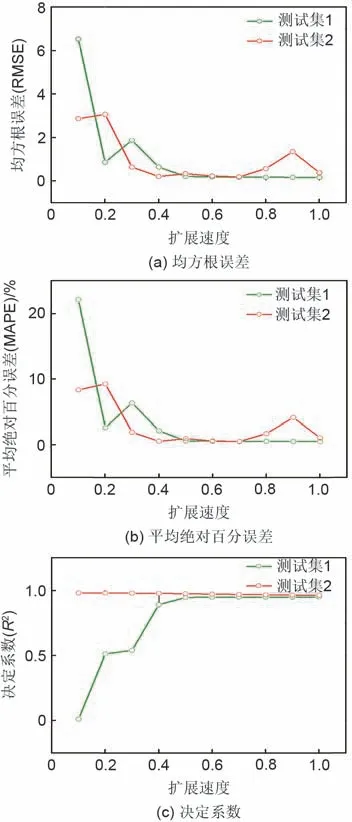
图5 扩展速度对RBF神经网络模型精度的影响Fig.5 Influence of expansion speed on model accuracy of RBF neural network

综上可见，扩展速度为0.7时RBF神经网络模型精度最高。对测试集1，在扩展速度为0.7 时，RMSE为0.74、MAPE为1.85%、R2为0.91。对测试集2，在扩展速度为0.7 时，RMSE 为0.188、MAPE为0.508%、R2为0.97，

图6(a)～(c)分别显示了GRNN 神经网络模型的均方根误差、平均绝对百分误差和决定系数随扩展速度的变化情况。图6(a)表示了均方根误差随扩展速度的变化。对测试集1，均方根误差随扩展速度的上升变大，最小均方根误差出现在扩展速度为0.2 时均方根误差为0.5。对测试集2，均方根误差在0.1、0.2时取得最小，然后随着扩展速度的增大而增大。图6(b)表示了平均绝对百分比误差随扩展速度的变化。与均方根误差随扩展速度的变化相似，对测试集1，平均绝对百分比误差随扩展速度的上升变大，最小平均绝对百分比误差出现在扩展速度为0.2时均方根误差为5%。对测试集2，均方根误差在0.1、0.2时取得最小，然后随着扩展速度的增大而增大。图6(c)表示了决定系数随扩展速度的变化。测试集1与测试集2具有相同的变化趋势，在0.2处取得最大值。

图6 扩展速度对RBF神经网络模型精度的影响Fig.6 Influence of expansion speed on model accuracy of RBF neural network

可见，扩展速度为0.2 时GRNN 神经网络模型精度最高，对相同测试集1，RMSE 为0.661、MAPE 为2.2%、R2为0.93，对相同测试集2，RMSE为0.77、MAPE为2.34%、R2为0.98。

将扩展常数为0.7的RBF神经网络模型与扩展速度为0.2的GRNN神经网络模型进行比较，发现扩展速度为0.7 的RBF 神经网络具有更好的性能。所以在本文之后的建模讨论中，均使用扩展速度为0.7的RBF神经网络模型进行建模讨论。

2.2 神经网络模型预测结果与原始值的比较

图7给出了平行流道质子交换膜燃料电池工作状态下温度分布的RBF神经网络模型预测结果与实验值的比较。点代表实验值，线代表RBF神经网络预测的结果。在电流密度为0.424、0.743、1.061三种情况下，预测值均能很好地贴合实验值。仅在电流密度为1.379 的情况下，靠近边缘的点(1-7、13-27)出现了少量的偏差，但是均在合理的误差范围之内。统计结果显示96%的模型的预测结果与原始值的相对误差在±5%以内。可以得出结论，对平行流道质子交换膜燃料电池，RBF神经网络模型预测的不同电流密度下的温度与实验值基本相同。

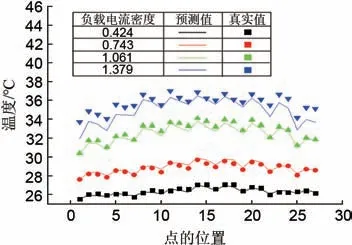
图7 平行流道质子交换膜燃料电池各电流密度下的RBF神经网络模型预测结果与实验值的比较Fig.7 Comparison of predicted results of RBF neural network model and experimental values at various current densities of PEMFC with parallel flow channels

图8给出了蛇形流道质子交换膜燃料电池工作状态下温度分布的RBF 神经网络模型预测结果与实验值的比较。点代表实验值，线代表RBF 神经网络预测的结果。在4种电流密度情况下，预测值变化趋势与实验室基本吻合，无较大的误差。统计结果显示95%的模型的预测结果与原始值的相对误差在±5%以内。

图8 蛇形流道质子交换膜燃料电池各电流密度下的RBF神经网络模型预测结果与实验值的比较Fig.8 Comparison between the predicted results of RBF neural network model and experimental values at various current densities of PEMFC with serpentine channels

可以得出结论，对平行流道质子交换膜燃料电池，RBF神经网络模型预测的不同电流密度下的温度与实验值基本相同。

3 结论

（1）提出了预测质子交换膜燃料电池膜电极组件温度的神经网络模型。结果表明，人工神经网络对质子交换膜燃料电池工作状态温度分布具有很高的预测精度。

（2）基于RBF 神经网络的平行流道质子交换膜燃料电池膜电极组件温度模型预测值与96%的实验值的相对误差在5%以内。基于RBF神经网络的蛇形流道质子交换膜燃料电池膜电极组件温度模型预测值与95%的实验值的相对误差在5%以内。

（3）人工神经网络对质子交换膜燃料电池工作状态下温度分布的高可预测性表明，神经网络可以在未来的研究中用于建模质子交换膜燃料电池装置，从而最小化实验耗时和实验花费。