基于场强角度的输电线路雷击概率定量评估

丁代筠，汪 旭，罗先俊

(四川能投发展股份有限公司，四川 成都 611130)

0 引 言

随着电力系统智能化、信息化进程的加快以及电力电子装备大规模的使用，雷电对电力的发展影响也越来越大[1-2]。目前全世界的输电线路快速增多，随之而来的是被雷击的概率越来越大[3]。因此，国内外学者对输电线路遭受雷击的现象进行了大量研究。

目前对输电线路雷击特性的研究主要有规程法和电气几何模型法。规程法依据输电线路实际运行经验构建，不能反映输电线路的物理特性，应用范围较少。文献[4-5]运用规程法进行防雷性能测试和评估，得出了规程法在实际应用的可行性。文献[6-8]通过考虑雷击环境、被击物材料等因素，使用规程法给出了上述因素对雷击性能的影响关系。在采用电气几何模型方面，该法因考虑了输电线路的自身结构及所处的环境因素等自身特性参数，在输电线路防雷计算中广泛采用。文献[9-11]以电气几何模型为基础，分别建立了输电线路和风电机组的防雷模型并给出了防雷措施。文献[12-14]分别从雷电建弧率和耐雷水平方面分析了雷电性能。但以上方法没有考虑到雷击线路的物理过程，其建立的雷击概率模型反映的雷击概率可解释性不强。

因此通过研究雷击导线时发生的物理过程，以雷击过程中产生的电场强度为切入点，详细刻画雷击过程，以此建立雷击概率模型并对雷击概率定量评估，精确反映雷击导线概率，进而指导选择合适的防雷方式和措施。

1 输电线路雷击过程及雷击概率定义

1.1 输电线路遭受雷击过程

当雷电下落的过程中，输电线路周围的表面场强将不断增大，随着雷电下行过程的逐渐发展，输电线路最先起始上行过程将与雷电下行过程产生连接，发生雷击，若其间的平均场强超过击穿临界值，则会发生击穿现象[15-16]。

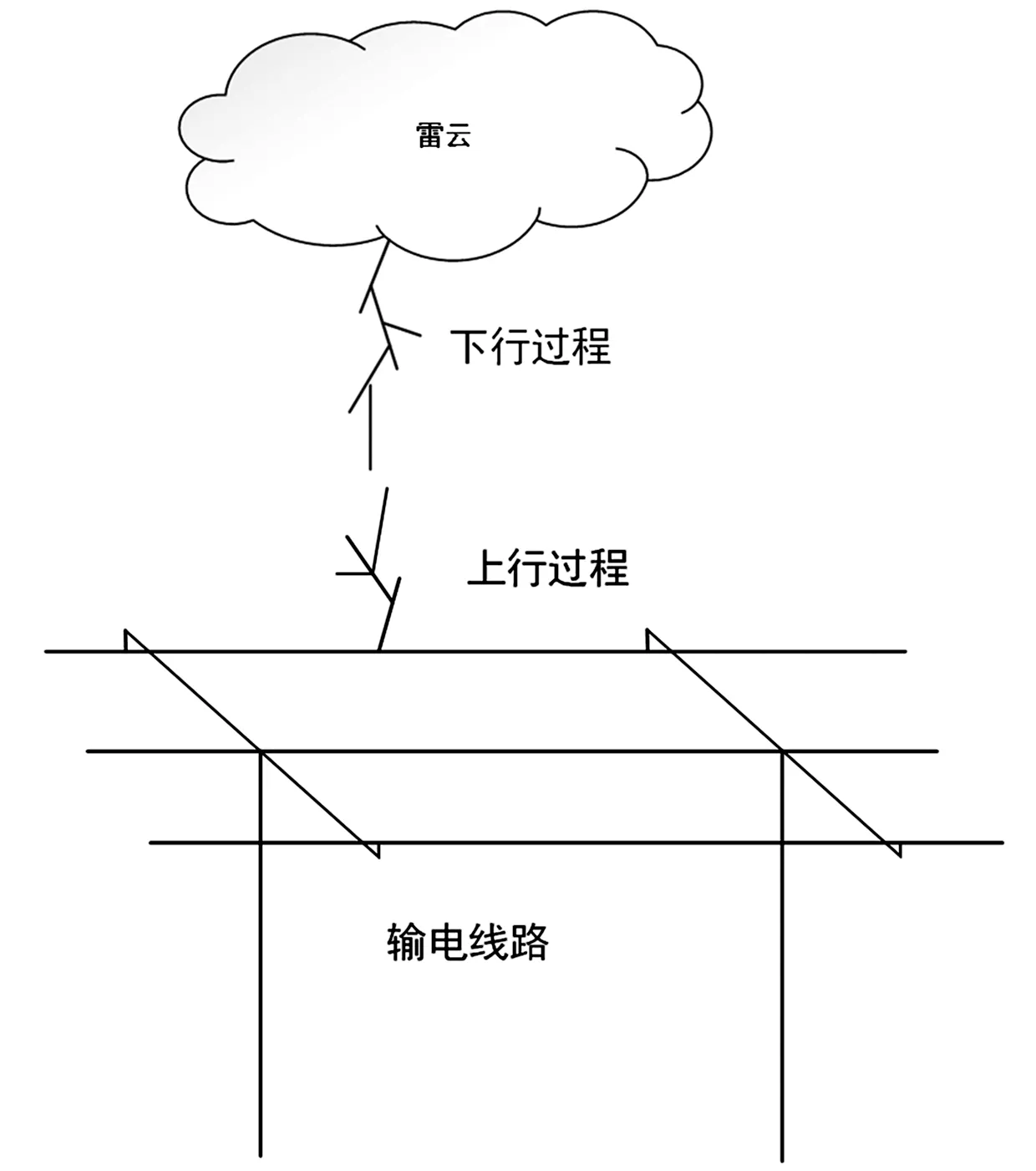
图1 输电线路遭受雷击过程

1.2 输电线路雷击概率定义

输电线路在雷电下行过程的作用下，容易发生起始上行过程，当上下过程连接时，将会发生输电线路雷击。雷击过程的产生与输电线路附近的场强、雷电发展过程有关，场强表示的是输电线路上行稳定起始过程的发生难度，场强越大，则输电线路越容易稳定上行，输电线路某一点i对应的场强Eav如式(1)所示。

(1)

式中：Ui为输电线路表面电势；Ud为上行电势；l为下行头部与上行或输电线路表面的距离。

当输电线路相导线某一点起始上行过程发生后，用输电线路各点的Eav与平均场强的最大值Emax的比值定义输电线路各点发生雷击的可能性，如式(2)所示。

(2)

式中，λ定义为输电线路相导线各点被击中概率。λ在相导线某区域积分与该区域面积S的比值，可定义为该区域的雷击概率p，如式(3)所示。

(3)

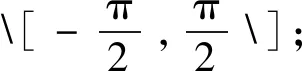
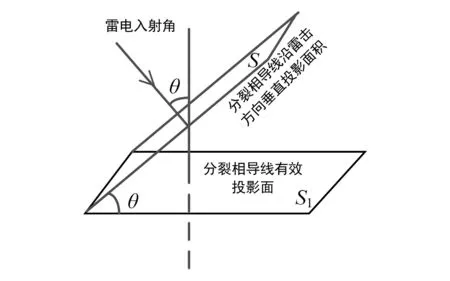
图2 相导线积分区域面积

因此，输电线路的区域整体雷击概率如式(4)所示。

(4)

式中：P为三相输电线路的区域整体雷击概率；Sj为每相导线有效面积，j=1,2,3，其为输电线路相数。

2 输电线路雷击概率评估模型

2.1 雷电下行过程通道场强分布模型

为了对输电线路雷击概率风险进行定量评估，需要建立雷电下行过程模型和输电线路上行过程模型，进而计算雷电下行过程头部与输电线路之间的平均电场强度分布情况，在此基础上量化分析线路各点被雷电击中的概率。

当输电线路处于雷雨天时，地面物体附近的电场受带电雷云和下行过程作用。雷云距地高度一般为2～10 km，并在近地产生约为10～20 kV/m的场强，这里取雷云产生的场强为-15 kV/m。雷电下行过程从雷云处开始，并随机向地面发展，由于雷电下行过程分支只能有限地影响地面电场，因此认为雷电下行以与地面垂直的方向向地面发展，并且不产生分支。

为了可靠准确地描述下行发展的实际物理过程，精确计算输电线路附近的电场变化，雷电下行过程通道场强分布模型采用式(5)[16]。

(5)

式中：ρ(τ)为雷电下行过程通道电荷密度，C/m；τ为雷电下行过程通道中某点到过程头部的距离；Hc为雷云高度；Hh为海拔高度；z0为雷电过程头部高度，m；Im为雷电流峰值，取30 kA；各已知系数分别为a0=1.476×10-5，a=4.857×10-5，b=3.91×10-6，c=0.522，d=3.73×10-3。

所建雷电下行过程通道场强分布模型的主要作用有2个：一是用来计算模拟雷电下行过程通道的电荷密度分布情况，其结果对上行过程通道的场强分布产生影响；二是根据该计算模型，通过COMSOL Multiphysics软件AC/DC计算模块进一步分析计算，得到考虑雷电下行过程的输电线路上行过程的场强分布。

2.2 输电线路上行过程通道场强分布模型

在雷电下行过程通道场强的作用下，地面物体附近的场强会发生畸变。由输电线路的雷击过程可知，输电线路上行过程通道场强的起始情况是决定雷击落点的主导因素。

在雷电下行过程通道场强的作用下，输电线路产生稳定上行通道的过程分为3个阶段，分别为初始电晕阶段、不稳定上行过程起始阶段和稳定上行过程起始阶段。

令电晕发生前的背景电位曲线为U1，电晕发生后的电位曲线为U2。电晕区内部场强为恒定值Ea，则U2如式(6)所示。

U2=Eaδ

(6)

式中，δ为距电极头部距离，m。

(7)

(8)

输电线路上行过程头部产生的电荷量ΔQ(i)为

(9)

式中，KQ为几何因数，KQ=3.5×10-5C/(V·m)，主要描述上行过程通道电位畸变情况和电荷间的关系。

(10)

式中，ql为满足流注时向过程通道转化时单位长度所需电量，ql=65 μC/m。

在计算上行过程发展场强的迭代过程中，依据工程经验，当上行过程长度大于2 m时，可认为从稳定上行过程开始。

2.3 影响雷击概率的关键因素分析

从解析法的公式着手，定性分析影响雷击概率的关键因素。

由式(1)、式(2)和式(5)可以看出，海拔高度、雷电入射角对雷电下行过程的场强分布有间接影响，进而影响输电线路的平均场强和对应的雷击概率，同时由公式可以看出雷击概率与海拔高度近似正相关关系。

由式(1)、式(2)和式(9)可以看出，海拔高度、雷电入射角对输电线路上行过程的场强分布是间接影响，首先对电极头部的距离产生影响，进而影响上行过程的电荷量，最后导致场强和雷击概率的改变。

本节从解析式角度对影响因素进行了定性分析，下面将从仿真的角度对该因素的影响定量分析，同时检验模型的正确性。

3 输电线路雷击概率评估步骤

通过对输电线路雷击的物理过程分析，考虑雷云电场、雷电下行过程通道电荷以及线路上行过程通道电荷的作用，建立起雷电下行过程通道和输电线路上行过程通道模型，分析输电线路附近的场强分布情况，进而得到输电线路雷击概率，其概率评估流程如图3所示。

图3 输电线路雷击概率评估流程

1)输入输电线路、雷云和雷电流初始参数。

2)雷电下行过程向下逐步发展，计算雷云和输电线路附近空间各点的电势和表面电荷密度。

3)根据是否存在稳定上行开始条件，判断是否计算输电线路的雷击概率分布。若上行过程长度大于2 m，将式(5)—式(10)所求得的参数代入式(1)和式(2)，求解出单位面积下的输电线路雷击概率，否则，返回至步骤2。

4)积分求解三相线路所求区域内的雷击概率。

4 仿真分析

基于仿真软件建立模型对输电线路雷击概率定量评估。模型的边界条件中，对线路和空气的分界面选用Dirichlet边界条件，空气选用第二类边界条件。考虑输电线路海拔高度的影响，以所提模型的解析方法和传统仿真方法进行对比分析，验证所提方法的可行性和准确性。其中传统仿真方法雷击概率是以直击雷跳闸率经过归一化近似等于。

如图4所示，在海拔高度0～4000 m的区间内，解析法和仿真法的雷击概率都处在4%～10.4%区间内，以海拔高度为自变量，对所提模型的解析方法和传统仿真方法进行对比，可以看出所提模型和传统仿真方法在相同海拔高度下所求得的输电线路雷击概率基本一致，验证了所提的基于场强角度的输电线路雷击概率评估模型的可行性和准确性。同时由图4可以看出随着海拔高度的升高，雷击概率逐渐增大，这说明了海拔高度与雷击概率呈正相关，在高海拔地区需加强输电线路的雷击保护。

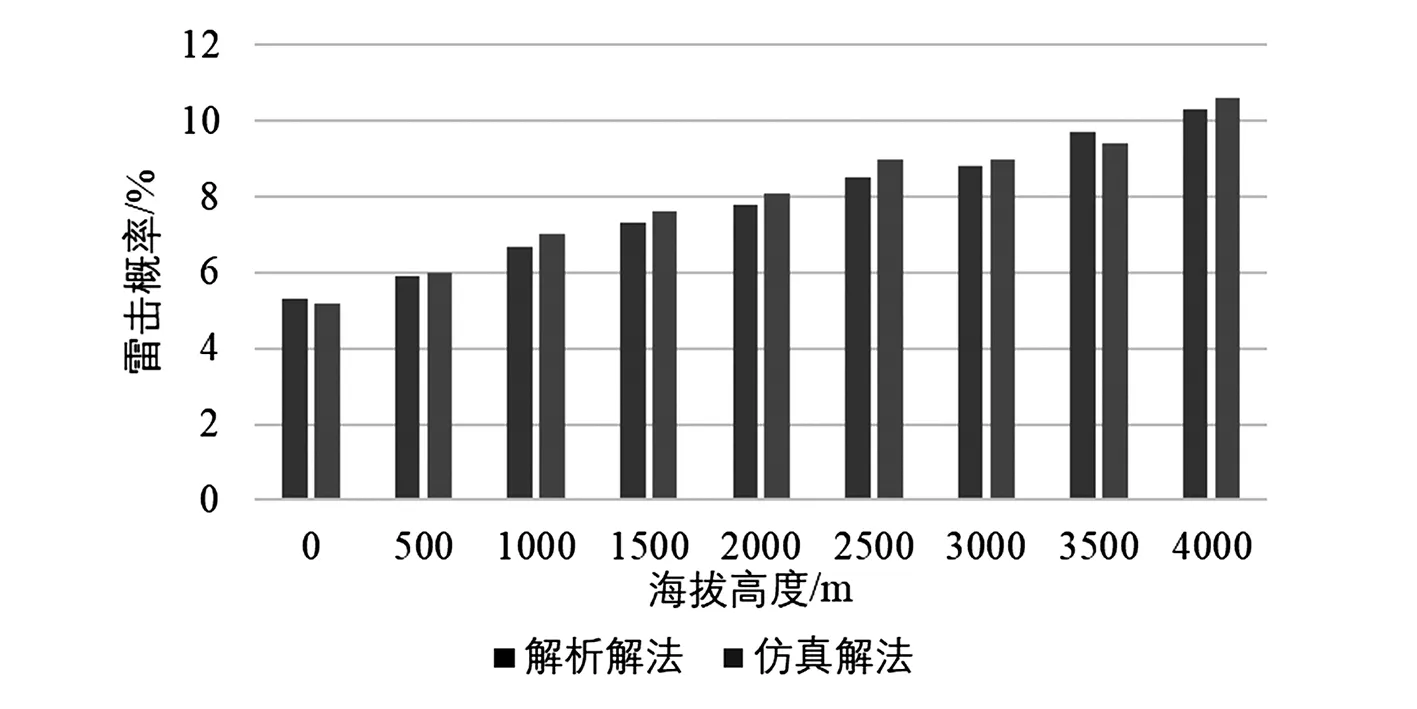
图4 不同海拔高度下的输电线路雷击概率对比

图5为输电线路雷击概率随海拔高度变化时解析法与仿真法的误差对比分析图。可以看出，解析法和仿真法误差范围在6%以内，因此可看出所提方法的有效性。

图5 不同海拔高度下雷击概率的解析法和仿真法对比误差

取图5数据进行定量分析，可得出如表1所示数据。

表1 解析法和仿真法误差分析(海拔高度)

由表1可以看出，所提方法和传统仿真法的平均误差、方差以及标准差分别为3.26%、1.25%和1.12%。可以看出，所提方法在不同海拔高度上的计算精度较稳定，其误差较小。由此也可说明了所提方法的可行性和准确性。

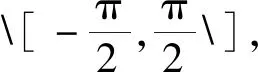
图6 不同雷电入射角下的输电线路雷击概率对比

由图6可知，当入射角为0o时，其雷击概率最大为9.4%，这是因为此时雷击通道与雷击面垂直，因雷击面积最大，故雷击概率最大，验证了所构建的雷击函数的正确性以及所提解析法的有效性。同时可以看出，随着入射角的逐渐增大，即雷击面积的逐渐减小，雷击概率在逐步减小，雷击概率范围在9.4%以下，说明了入射角与雷击概率呈负相关关系。

在此基础上通过仿真数据量化解析法准确程度。对图6数据进一步分析，求取两种方法对比误差，可得图7所示结果。

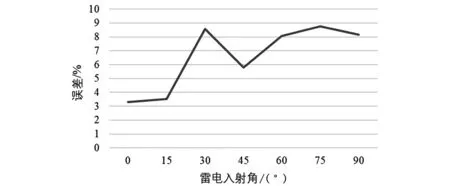
图7 不同雷电入射角下雷击概率的解析法和仿真法对比误差

由图7可知，解析法和仿真法两者之间的误差在9%以内，也证明了所提方法的可行性和有效性。同时，取图7的数据定量分析，可得如表2所示数据。

表2 解析法和仿真法误差分析(雷电入射角)

由表2可以看出，所提方法和传统方法的最大误差为平均误差6.60%，其标准差为1.54%，可以看出，误差整体上较小，所提方法稳定性较高。

5 结 论

从输电线路雷击概率的物理过程出发，以场强角度为基础，定量评估了输电线路的雷击概率，得到了如下结论：

1)分析了输电线路遭受雷击的物理过程，从场强角度出发，建立了输电线路的雷击概率模型。

2)依据实际雷击物理过程，建立了雷电下行过程通道场强模型和输电线路上行过程通道场强模型，进而量化了输电线路的雷击概率，得到了输电线路雷击概率解析模型。

3)分析了影响雷击概率的关键因素，得到了海拔高度和雷电入射角度对雷击概率影响的程度。通过输电线路雷击概率解析模型与经典仿真模型进行对比，说明了所建解析模型的可行性和正确性，同时由于解析模型还原了输电线路遭受雷击的物理过程，因此所提模型更精确。

虽然以输电线路遭受雷击的物理过程为基础进行了建模评估，但未考虑输电线路所在的环境(如土壤电阻率、环境污秽程度等)对输电线路的深入影响，下一步将对该部分进行研究分析，优化完善模型。