软土场地热固结对能源桩受力特性的影响研究

俞 磊,邓岳保*,张付林

（1.宁波大学 土木与环境工程学院,浙江 宁波 315211;2.宁波市轨道交通集团有限公司,浙江 宁波 315012）

随着社会进步和工业化进程的加快,全球气候变暖和传统不可再生能源消耗等问题的严重性逐渐凸显,研究和开发可再生能源变得尤为重要.我国“碳达峰”和“碳中和”目标的提出,进一步推动了当下节能环保技术的发展.能源桩通过降低建筑空调能耗,在节能领域受到广泛关注.能源桩不同于常规桩,该技术通过在桩基施工中埋设换热管,利用地下土壤、地下水温相对稳定的特性进行浅层地温能转换,既满足了经济节能的需要,又节约了建筑用地[1].

能源桩承载与变形特性研究是研发推广这一技术的关键任务之一.对此,国内外学者围绕能源桩传热性质和热-力耦合下的承载特性开展了一系列研究.在传热性质方面,Abdelaziz 等[2]对平衡环境干扰下岩土体的导热系数进行了测试,提出更准确的评价能源桩换热性能的方法.崔宏志等[3]利用相变材料来提高混凝土能源桩的换热性能,在制冷工况下对能源桩以及桩周土的热响应进行了分析.桂树强等[4]在南京某项目桩基中埋设换热 管,并进行了热响应测试,发现钻孔埋置换热管能源桩具有更好的换热性能,也更经济.关于热-力耦合下能源桩承载特性研究方面,Knellwolf 等[5]在能源桩承载特性分析中引入荷载传递法,考虑了温度场、应力场和桩土之间的相互作用,提出了考虑热-力耦合的传递分析方法,但该法存在迭代过程繁琐、无法反映土体变形时间属性等问题.黄胤培等[6]提出了基于指数函数模型的能源桩热-力耦合传递分析方法.宗宸锋等[7]进一步基于该指数模型提出了考虑径向温度效应的荷载传递法.董龙龙等[8]基于荷载传递法,提出考虑指数模型的能源桩长期响应分析法.上述研究主要围绕能源桩桩体受力特性开展.

在我国沿海软土地区(如宁波)的能源桩应用中,发现热交换对场地土层的不均匀沉降有一定影响.实际上,在能源桩运行过程中,场地温度变化对土骨架位移、孔隙水压力变化都会产生影响,同时还对桩-土接触面力学特性产生影响.已有土性研究表明[9-12],土体力学性质随地基内温度的变化而变化.相对而言,软土力学性质的温度效应更为明显.因此,能源桩受力特性研究有必要综合考虑软土力学特性的温度效应.

本文考虑桩-土接触面力学特性,基于改进佐腾悟双折线模型[13],结合文献[14-15]提出的热力耦合模型和太沙基一维固结理论,推导建立了考虑桩周土体热固结的能源桩荷载传递模型.在此基础上,分析能源桩温度变化对桩-土界面侧摩阻力的影响,探讨热-水-力耦合作用下能源桩的长期受力特性.相关研究可以为软土地区能源桩设计提供参考.

1 计算模型与控制方程

1.1 计算模型

图1(a)为轴向荷载下桩的荷载传递法的计算模型,桩侧和桩端通过线性弹簧与桩周土连接.随着桩周土的热固结,弹簧和支座会随着土层固结一起下降(图1(b)).该模型可以用来计算能源桩桩周土体产生的负摩阻力.

图1 计算模型

1.2 热固结沉降计算

为简化计算,假定:(1)在能源桩热交换作用下,桩周土瞬时升温,然后温度保持恒定;(2)桩周土层为顶部透水、底部不透水状态;(3)不考虑打桩引起的超静孔隙水压力对地基土固结沉降的影响;(4)忽略桩体对地基土体热固结沉降的影响.

根据已有土性研究[14-15],加热使土体表观先期固结压减小,从而影响土体压缩性质.Cekerevac等[14]提出了先期固结压力和温度变化的关系式:

式中:ΔPcT为先期固结压力变化量;γT为先期固结压力的温度影响参数,通常取0.3～0.4;PcT为温度为T时土体的先期固结压力;ΔT为温度变化量.

基于式(1),结合土体应力e-p曲线法,可得考虑温度影响的土层沉降计算公式为[15]:

式中:Sc为土层沉降量;H为土层厚度;e0为土体初始孔隙比;Ce为土体回弹指数;Pc为土体初始有效自重应力.

进一步引入太沙基一维固结公式:

式中:Uz为不同深度处土的固结度;t为固结时间;Cv为固结系数;Hw为排水距离;z为深度;m取1,3,5,….

由此可得任意时刻土层的固结沉降.

把桩周土沿深度方向划分为n层,每层总沉降量为Sc/n.式(3)中通过假定时间t,可知在该时刻沿深度方向的固结度.每层土体的沉降量Sz等于该层的固结度乘该层总沉降量,其计算公式为:

叠加各土层的固结沉降,可得任意时刻场地的固结沉降.

1.3 控制方程

在桩上取一单元体(图2),结合单元体的静力平衡条件和桩顶轴力作用下的压缩变形,可得单桩轴向荷载传递的基本微分方程:

图2 桩体微段

式中:S为桩身某点竖向位移;U为桩体周长;A为桩身截面面积;Ep为桩体的弹性模量;τz为桩侧摩阻力.

由于软土地区桩周土的热固结沉降,土体会相对于桩产生向下位移,从而对桩侧表面产生负摩阻力.赵明华等[13]在佐腾悟双折线模型基础上,针对不同桩土相对位移引入负摩阻力概念,开展了对桩侧摩阻力的计算.为简化计算,在文献[13]计算模型基础上进行改变,其数学表达式为:

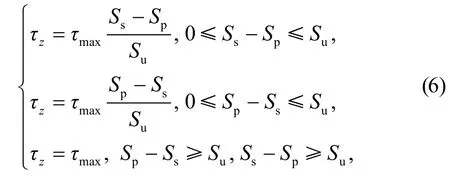
式中:Sp和Ss分别为桩身位移和桩周土位移;τmax为桩侧最大摩阻力;Su为桩土临界位移,取5 mm[16].

Vijayvergiya[17]对桩侧土体为黏土时提出最大摩阻力的表达式为:

式中:λ为无量纲摩阻力系数[18];σm为地表至桩尖范围内土的竖向有效应力的平均值;Cm为桩身范围内土的不排水抗剪强度平均值,其表达式为:

式中:γ为土体的容重;c(T)和φ(T)分别为黏聚力c和摩擦角φ关于温度T的函数.

根据文献[19],其表达式为:

联立式(5)～(8)可得耦合温度的传递模型控制方程:

式中:ΔS为Sp和Ss的差值.具体由桩土相对位移来判断.

2 求解

2.1 控制方程的离散

将桩体分为N段,当N足够大时,有:

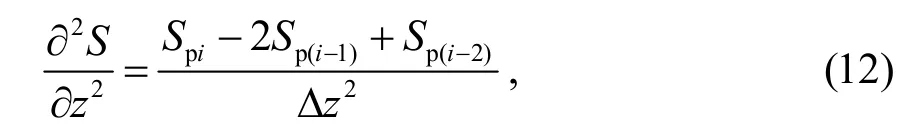
式中:Spi为桩身第i个微端顶部位移.联合式(6)、式(11)和式(12)得:

当Ssi-Spi＞Su时,

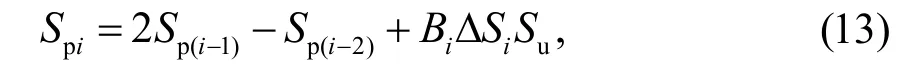
为了区分微端,取ΔSi=1.

通过式(13)～(16)可列出n-1个方程组,共有n+1个未知量.因此,为了求解全部的未知量,需要通过引入2个边界条件求解.在桩顶上再虚设一桩节,该桩节侧面无摩擦力,仅受外力Q和桩顶的支撑作用.该桩节位移可表达为:

式中:Sp0和Sp1分别为桩顶虚设桩节顶部位移和桩顶的位移.

由桩端受力平衡可得:

式中:L为桩侧;Kc为基底反力系数;Spn和Ssn分别为桩端处桩身位移和桩周土位移.

从式(3)和式(4)可知,热固结随时间变化导致桩身方向产生非线性位移.

2.2 数值分析

在荷载传递法计算中,周国林[20]提出一种数值解法.首先假设桩头位移为某一数值,根据递推关系计算出桩尖位移Sb和荷载Pb;然后用传递关系算出在Pb作用下桩尖位移Sb′,将2 种算法算出的桩尖位移进行比较,直到无限接近为止.参考该算法,本文的具体计算步骤为:(1)按精度要求,将桩划分为N个单元,假定第i个桩单元顶部的位移为Spi;(2)通过式(4)计算得某一时刻桩周土由于温度影响产生的位移Ssi;(3)假定桩顶位移Sp1;(4)判断该单元桩土相对位移是否超过临界位移,如果超过,用桩侧最大摩阻力τmax作为该单元的摩阻力,否则进行下一步;(5)应用边界条件式(17)联合式(13)～(16),用递推关系可得桩身位移Spi和桩侧摩阻力τni;(6)把桩侧摩阻力τni和桩段处桩周土位移Ssn带入边界方程式(18),求解得到Spn′;(7)如果|Spn-Spn′|≤ε,满足精度要求,否则返回第3 步,重新计算至满足要求;(8)最后可算出桩身侧摩阻力分布、桩身轴向力分布与时间的关系.具体计算流程如图3 所示.

图3 桩身沉降和侧摩阻力随热固结时间的发展流程

3 算例与分析

3.1 计算参数

通过引入模型地基对该计算模型进行分析.模拟土层分布及参数见表1.

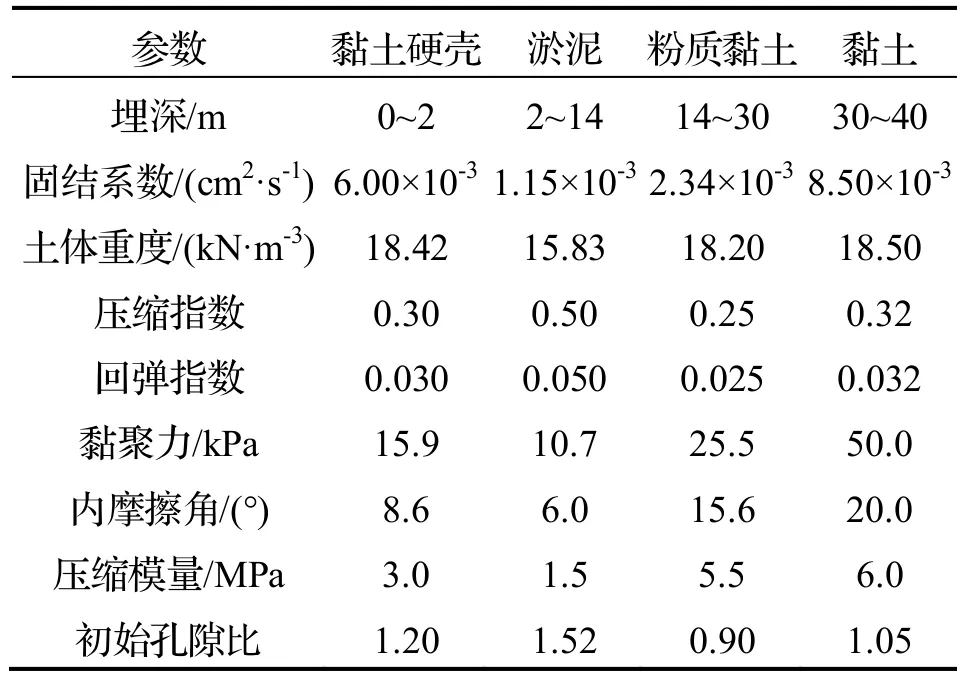
表1 模型土层分布及其物理特性参数

模型参数为:桩长40 m,桩径0.6 m,桩身弹性模量30 GPa,桩顶外加荷载3 000 kN,τmax发挥时桩的临界位移5 mm,基底反力系数3 000 N·mm-1,室温20 ℃.

3.2 结果分析

3.2.1 侧摩阻力及轴力

图4 给出了在桩周土温度上升15 ℃时,桩周土层由于固结时间(30、70、120、170、240 d)增加引起桩侧摩阻力的变化.在软土中,桩身负摩阻力沿桩身呈先增大后减小趋势,当减至0 后由于受到桩端持力层向上的作用力,从而产生正的摩阻力.由图4 可知,随着固结时间的增加,最大负摩阻力由-1.78 kPa 变为-14.39 kPa,且位置逐渐下移.中性点深度比为0.14～0.68,随着固结时间的增长,中性点位置从5.60 m 逐渐升至27.17 m 左右.

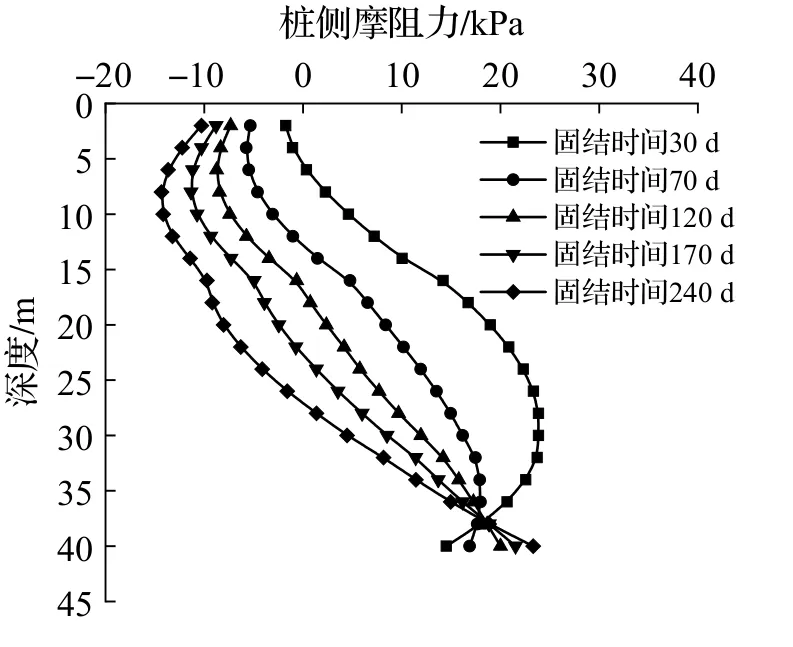
图4 热固结对侧摩阻力的影响

沿桩深方向将图4 负摩阻力换算为轴力.以桩身受拉为正、受压为负可绘制桩身轴力随固结时间(70、120、170、240 d)的发展曲线(图5).

图5 热固结对桩身轴力的影响

软土热固结沉降引起的负摩阻力会在桩身表面形成下拉荷载,在固结时间为70 d 时下拉荷载仅为95.05 kN,而在固结时间为240 d 时其值增至487.89 kN.这是由于桩土滑移不断增大,中性点逐步下移而导致负摩阻力增长,桩周土对桩身表面向下作用力不断增长而导致下拉荷载的增加.

图6 给出了在固结30 d 时不同温度(30,50,80 ℃)条件下桩侧摩阻力的变化.由图6 可知,当桩周土体温度为30 ℃时,最大负摩阻力为-1.78 kPa,中性点位置在桩身5.60 m 处;当桩周土体温度为50 ℃时,产生最大负摩阻力为-16.28 kPa,中性点位置在桩身17.22 m 处;当桩周土体温度为80 ℃时,产生最大负摩阻力为-34.90 kPa,中性点位置在桩身29.92 m 处,其温度较室温分别上升了15、30、50 ℃.由于温度上升改变了土层的压缩性,致使土体先期固结压力减小,桩周土场地沉降增加,在相同固结时间产生更大的土体相对于桩向下的位移,造成负摩阻力增加,中性点位置沿桩身向下移动.

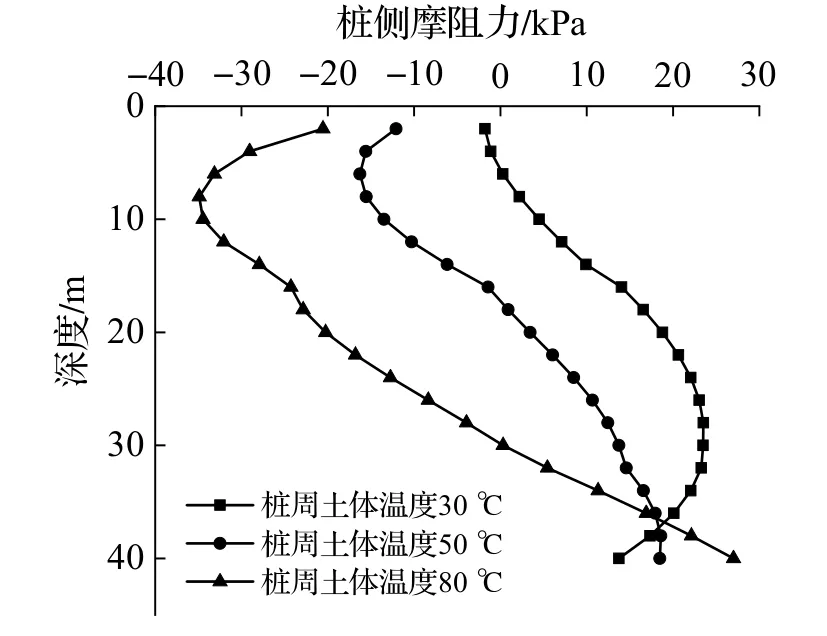
图6 固结30 d 时温度变化对桩侧摩阻力的影响

3.2.2 桩身沉降

图7 给出了不同固结时间桩身的位移曲线.

图7 热固结对桩身沉降的影响

由图7 可见,桩身位移曲线整体向右移动,且右移速度呈减小趋势.这是由于桩周土内升温所产生的超静孔隙水压力消散趋于完成,其消散导致桩周土的沉降增加逐渐减少,进而导致桩身位移沉降的增加减缓.随着桩周土体固结时间增加,桩顶和桩端都发生一定程度的下沉,桩顶处沉降在14.15 mm 至14.40 mm 之间,桩端处沉降在0.41 mm 至1.69 mm 之间.受升温影响,桩周土的热固结沉降会引起桩体下沉,而桩-土之间相对位移的改变会对桩身侧摩阻力的分布产生重要影响.

4 结论

(1)通过考虑升温对土体压缩性质的改变,建立了考虑桩周土温度影响的桩侧摩阻力计算模型,并详细分析了桩周土热固结沉降对桩身受力特性和沉降规律的影响.

(2)桩周土升温时,土体发生热固结沉降,桩侧负摩阻力和中性点位置发生变化.中性点位置随固结时间的增加而上升,由此导致桩侧负摩阻力增加.升温对土体压缩性质的改变是影响桩身侧摩阻力的主要原因.相对来说,由升温导致的土体黏聚力和内摩擦角的降低对桩侧摩阻力变化影响较小.

(3)受升温固结影响引起的桩身沉降随时间推移而增长,当土中孔压消散趋于完成时桩身沉降也趋于稳定,温度变化对桩身沉降的影响不大.