波壁管中脉动流动的数值模拟

张 亮，张安龙，荆宇燕，曲平平，田林超，陈贺敏

(1.燕山大学车辆与能源学院，河北 秦皇岛 066004；2.燕山大学信息科学与工程学院，河北 秦皇岛 066004)

如今能源紧缺问题日趋严重，如何能够合理的利用能源已经成为了当今各国工业发展的核心问题，为了缓解能源紧张的问题，各国都在寻找新的能源或者节约能源的方法，而换热器在能量传递方面发挥着重要作用[1].换热器中直接参与换热的部分为换热管，它的换热效率往往能够直接影响到换热器的效率.脉动流动对管内流体的强化具有很重要的意义，一些学者对此进行了研究.杨卫卫等[2-3]利用数值模拟的方法对对脉动流场下的平直管道与凹槽管道内流体的传热与阻力特性进行研究，研究结果表明，脉动流动下的换热特性与阻力特性与定常流场相比，有很大的不同，脉动流场的壁面摩擦系数呈现正弦规律变化；同时还发现，脉动流动加强了管内流体的扰动与掺混作用，增强了流体的换热能力.林延溥[4]对脉动流场下的波壁管质量传递强化的影响因素进行了分析研究，研究结果表明，质量传递强化因子E在中等雷诺数下最大，在较低与较高雷诺数下都减小，在P<1时，质量传递强化因子E的变化不明显，而在P>1时，E随着P的增大而增大.武慧朝[5]对脉动流场下波壁管流路中的质量强化机理进行实验研究，结果发现在P>1时，在净雷诺数接近并超过临界雷诺数并伴有反向流的情况下，满足共振强化的两个特性，即三维管路中也存在着共振传递强化.Nishimura等[6]对波纹管内脉动流场进行了可视化实验研究，实验结果表明，波纹流道内产生的漩涡能够加强波纹管内流体的掺混，且流体的流速能够影响漩涡的生成；同时还发现脉动流场下波纹管内流体的换热特性与阻力特性与定常流场相比相比具有很大的差异.Grassmann等[7]对圆管内的振动与脉动传质强化进行了实验研究，结果表明，与定常流场相比，振动与脉动都会起到强化传热的效果.Lee等[8]通过数值模拟的方法对轴对称正弦波壁管的质量传递特性进行了研究，结果表明，质量传递强化因子E随雷诺数Re的增大而增大，同时还发现，每一个雷诺数都对应着一个最佳的St数，最佳St数随雷诺数Re的增加而小幅下降.

综上所述，虽然前人对波壁管下的脉动流场进行了一些研究，但大部分都是进行的质量传递特性的研究，对脉动流场下波壁管内流体的换热特性与阻力特性还未有进行系统研究，故本文利用数值模拟的方法，对脉动流动下波壁管内流体的流动和换热特性进行研究.

1 几何模型

波壁管结构如图1所示，管子最大直径Dmax=10 mm，最小直径Dmin=3 mm，波长λ=14 mm，波幅A=3.5 mm，管子两端各留有一段长为14 mm的直管壁，管子总长度为L=224 mm.

图1 波壁管结构示意图

2 脉动流场的形成

脉动流是由一个稳定流与一个强制振动流相互叠加而成，脉动流的形成如图2所示.脉动流的流量是随时间呈正弦规律变化，其表达式为

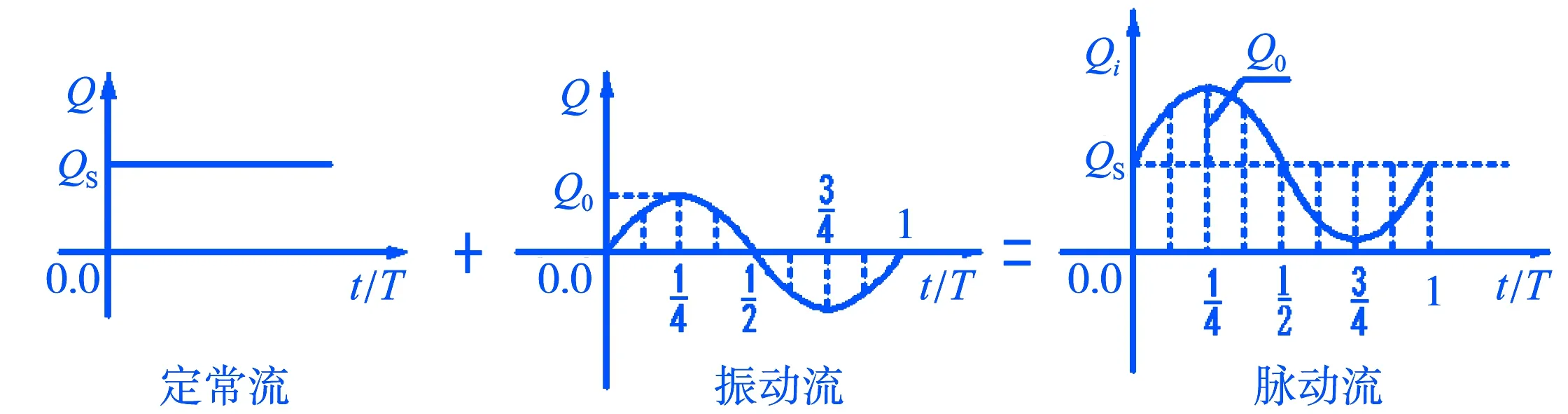
图2 脉动流的形成

Qi=QS+Q0sin(2πt/T)，

(1)

公式中：QS为定常流场下的流量；Q0为振动流的最大流量，且

(2)

公式中：f为活动泵的频率；s为冲程；DP为活动泵的活塞直径.

脉动流场下的主要参数为净雷诺数Res、斯德鲁哈尔数St以及振动分率P.它们的表达式依次为

(3)

(4)

St=Dmax(2πf/u)，

(5)

公式中：P为振动流的最大流量与定常流的流量之比，反映了振动幅度的大小.如图3所示，当P<1时，振动流的最大流量小于定常流流量，此时，不会出现反向流；当P=1时，即振动流的最大流量等于定常流流量，此时，t=3/4T时，叠加后的流量为0；当P>1时，振动流的最大流量大于定常流流量，此时，会出现反向流的情况.

图3 不同振动分率P下的脉动流流量随时间的变化关系

3 网格无关性验证

由于波壁管的独特的管型结构，使得管内流体的流场变化剧烈，故本文网格类型选用具有更高适应度的四面体非结构性网格，网格最小尺寸为0.12 mm，最大尺寸22.5 mm，网格质量平均值为0.72.为了排除网格数量对模拟结果的影响，需要对此进行网格无关性验证，对波壁管划分了7种不同数量的网格.得到了波壁管进出口平均压降随网格数量的变化规律如图4所示，综合考虑了计算精度与设备仪器等因素，将网格数量控制在20万左右.

图4 压降随网格数量的变化

在数值模拟计算过程中，做出如下假设：流体的物性参数恒定，即不受温度和压力等条件的影响；壁面固定，且保持壁面无滑移状态；在流体流动及换热过程中，不考虑重力与壁面粗糙度的影响.边界条件设置：入口采用速度入口，采用UDF脉动速度，入口流体温度为300 K；出口设为自由出口；壁面采用固定壁面，壁面温度恒定，设为350 K.在FLUENT模拟计算中，由于Re>236时，波壁管内流体从层流过渡为湍流[9]，故采用湍流模型中的RNGk-ε模型，压力耦合求解采用SIMPLE算法，由于采用的是非稳态计算，根据不同工况来设定不同的时间步长(Time Step Size)与时间步数(Number of Time Steps)，两者的乘积等于不同工况时的周期T，计算精度设为10-4.进口UDF脉动速度可由公式(1)、公式(3)、公式(4)公式(5)推出.其表达式为

(6)

4 计算结果分析

4.1 波壁管内流体的流场分析

图5 脉动流动下的流场分布

4.2 换热特性分析

定义一个无量纲量传热强化系数，表示脉动流场下一个周期T的平均Nu与相对应定常流场下的Nu之比.其表达式为

(7)

公式中：Num为一个脉动周期下的平均Nu；Nus为相对应定常流场下的Nu[10].

脉动流场斯德鲁哈尔数St=0.5时，雷诺数Re与振动分率P对传热强化系数Eh的影响，如图6所示.从图6中可以看出，传热强化系数Eh均大于1，表明脉动流场是能够强化传热的，随着雷诺数Re的增大，传热强化系数是先增加后减小的，存在一个最佳的Re，使得强化传热效果最好.此外，随着振动分率P的增加，传热强化系数Eh不断增大，这与文献[4]林延溥得到的质量传递强化因子E的变化相类似.

在脉动流场下振动分率P=0.6时，斯德鲁哈尔数St对传热强化系数Eh的影响如图7所示，随着斯德鲁哈尔数St的增加，传热强化系数Eh随之增大，即传热强化效果不断增强.这是由于随着St的增大，由公式(5)可知，脉动流的频率随之增加，致使波壁管内流体的速度梯度的变化速率增大，从而产生更多的漩涡，增强管内流体的湍流度，减薄了热边界层，降低了传热热阻，增强了传热效果.

4.3 摩擦阻力系数分析

在流动过程中，强化传热不应该以大幅增加摩擦阻力系数为代价，故需要对摩擦阻力系数进行系统的分析.摩擦阻力系数的表达式为

(8)

公式中：Dmax为波壁管的最大直径，m；ΔP为进出口压降，Pa；L为波壁管管长，m；u为流体平均速度，m/s；ρ为流体的密度，kg/m3.

脉动流场下雷诺数Re=400时，斯德鲁哈尔数St与振动分率P对一个脉动周期下的平均摩擦系数fm的影响，如图9所示.从图9中可以看出，随着振动频率P的增大，平均摩擦系数fm增大；然而随着斯德鲁哈尔数St的变化，平均摩擦系数fm几乎不发生变化.

脉动流场下振动分率P=1时，雷诺数Re对平均摩擦系数fm的影响.随着雷诺数Re的增大，平均摩擦系数fm在不断降低，且降低的幅度在减小，如图10所示.

图10 Re对平均摩擦系数fm的影响

5 结 论

本文对脉动流场下波壁管内流体的换热及阻力特性进行了数值研究，主要结论如下：

(1)与定常流场相比，脉动流场能够强化波壁管内流体的换热，随着Re的增大，传热强化效果先增加后减小；传热强化系数与斯德鲁哈尔数St以及振动分率P均成正比关系.

(2)摩擦阻力系数整体呈现正弦规律变化，在较低St时，随着St的增加，摩擦系数几乎不发生变化，而在较大St时，随着St的增加，摩擦系数明显发生变化，但与定常流场相比，平均摩擦系数变化不明显.

(3)随着斯德鲁哈尔数St的增大，平均摩擦系数fm几乎振动分率P的增大，平均摩擦系数随之增加；平均摩擦系数随着雷诺数Re的增大而逐渐减小.