毫秒延时爆破等效单响药量计算及振速预测 *

何 理，杨仁树，钟东望，李 鹏，吴春平，陈江伟

（1.北京科技大学土木与资源工程学院，北京 100083；2.武汉科技大学冶金工业过程系统科学湖北省重点实验室，湖北 武汉 430065；3.长江科学院水利部岩土力学与工程重点实验室，湖北 武汉 430010；4.矿冶科技集团有限公司，北京 100160；5.中国建筑第七工程局有限公司，河南 郑州 450004）

爆破工程实践中，质点峰值振动速度vp的预测最常用的方法是基于经验公式对振动实测数据进行回归统计分析[1-5]。其中，比例距离公式用于振动实测数据回归分析最为简单方便，是国内外爆破从业人员进行vp预测的首选[6-9]。vp回归分析预测的关键在于准确确定比例距离公式中各测点峰值振速对应的单响药量Q与爆心距R。然而，大量理论与试验研究表明，短毫秒延时爆破情况下，相邻段别爆破地震波产生干扰叠加，难以高效、准确确定实际单响药量[10]。有学者提出了短毫秒延时爆破情况下等效单响药量的取值方法[11-15]，然而借助萨道夫斯基公式利用现场爆破振动实测数据进行回归分析时，回归分析的相关性并不高，近距离的爆破振动峰值计算误差最高达200%～300%，远距离的计算误差也很大[16]。因此，考虑分段爆破地震波叠加因素对单响药量取值的影响，提出可行的等效药量取值方法有待进行深入研究。鉴于此，许多科研人员通过概率算法[17]、遗传算法[18-19]、BP神经网络方法[20]、分类回归树方法[21]、粒子群算法[22-23]等数值方法对生产爆破实践中振动速度进行预测，大大提高了预测精度。除此之外，也有研究人员开展单孔化爆试验测得种子基波，在考虑传播场地介质属性对地震波衰减耗散因素的基础上，借助计算机技术通过线性[24-26]或非线性叠加[27-28]模拟群孔爆破地震波时程，进而对vp进行预测，还可对群孔爆破地震波时频域信息进行准确解读。尽管这些先进的技术和方法能够提高vp预测精度，而且可获取更为丰富的地震波时频域信息，然而这些方法的应用均是以复杂的计算机程序编制以及反复的程序试算为代价的，时间与资源成本较高。并且均是基于复杂、严密的数学方法或理论，对于从事生产爆破的工程技术人员而言，应用起来不够便捷高效。因此，建立简单、有效并适合工程师现场应用的vp预测方法具有极大工程实际意义。

非电起爆网路中由于雷管延时误差原因，一方面，致使相同段号的雷管延时存在离散现象，致使同排炮孔齐发爆破时各单孔并非在同时刻起爆；另一方面，可能会导致相邻段别地震波产生干扰叠加现象，从而无法准确确定单响药量，这些因素都给爆破振动速度回归分析及vp预测带来较大困难。设计开展单孔爆破与多排孔毫秒延时爆破振动试验研究，系统研究群孔分散装药齐发爆破时的等效药量取值方法，在此基础上考虑毫秒延时爆破分段振波叠加效应，通过引入振波叠加因子，建立短毫秒延时爆破振动速度的预测方法，为工程爆破一线技术人员快速、高效评估爆破振动效应及其危害提供借鉴。

1 爆破振动试验研究

1.1 场地概况

某石油储备基地扩建项目位于剥蚀低山丘陵地貌区，设计规模为3×106m3，布置1×105m3储油罐30个。项目涉及山体边坡开挖与下穿隧道掘进爆破，设计边坡共分9级放坡，每级平台宽度3 m，山体开采最高标高为+130 m，最低标高为+4.0 m，坡角范围为20°～45°。山体表面多为黏土或粉质黏土，厚度不等，往下分别为全风化、强风化、中风化、微风化晶屑玻屑凝灰岩，大部岩体中等硬度，可爆性和可钻性都较好[3]。爆破试验拟在坡体高程约+47 m平台开展。

1.2 装药结构与爆破参数

试验分为2组，第1组试验包括2次单孔爆破振动监测，第2组试验利用塑料导爆管雷管设计非电起爆网路开展多排孔毫秒延时爆破振动监测，采用连续柱状装药结构，炮孔装药结构如图1所示。振动监测试验爆破参数如表1所示。

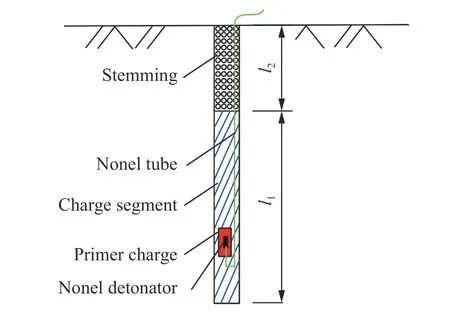
图1 炮孔装药结构Fig.1 Charge structure of blast-hole

表1 爆破参数Table1 Blasting parameters

多排孔毫秒延时起爆网路设计见图2，图2中孔外传爆雷管选用MS3段，孔内起爆雷管选用MS11段。图2所示毫秒延时起爆网路装药量统计见表2。

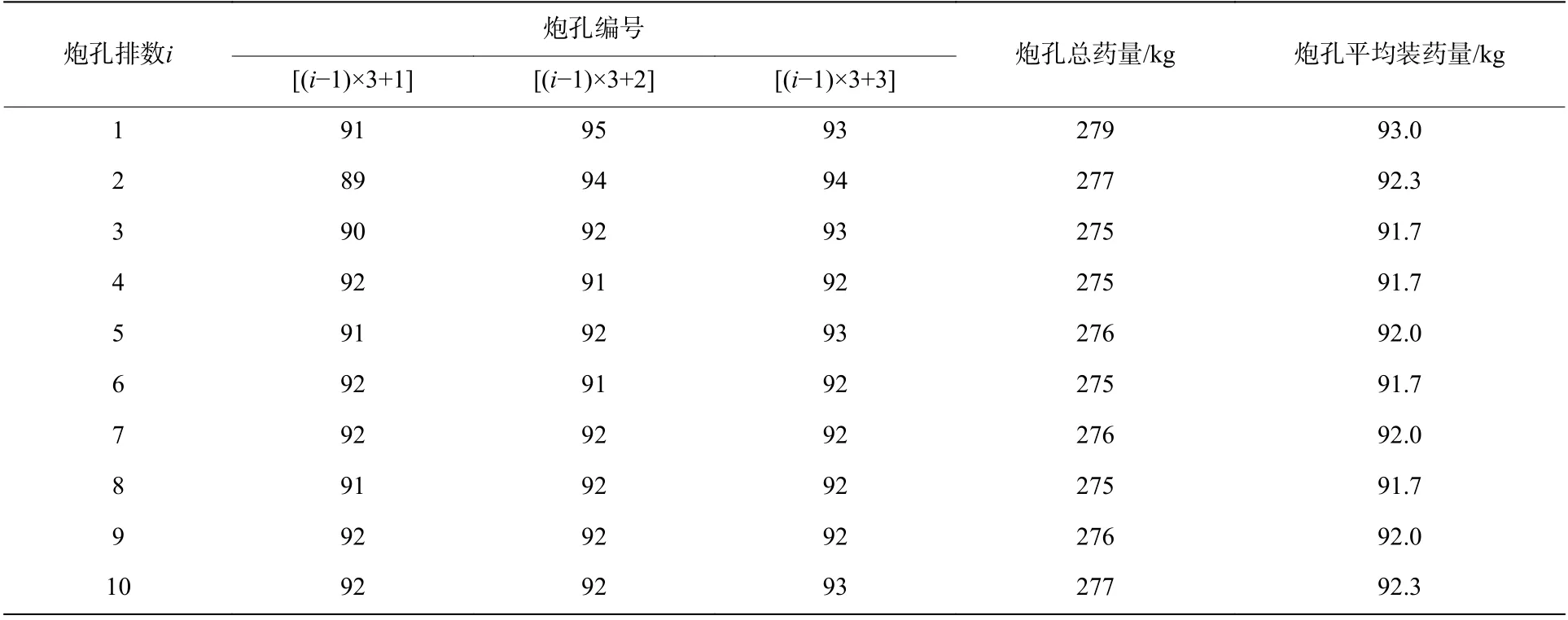
表2 毫秒延时爆破药量统计Table2 Charge statistics of millisecond delay blasting

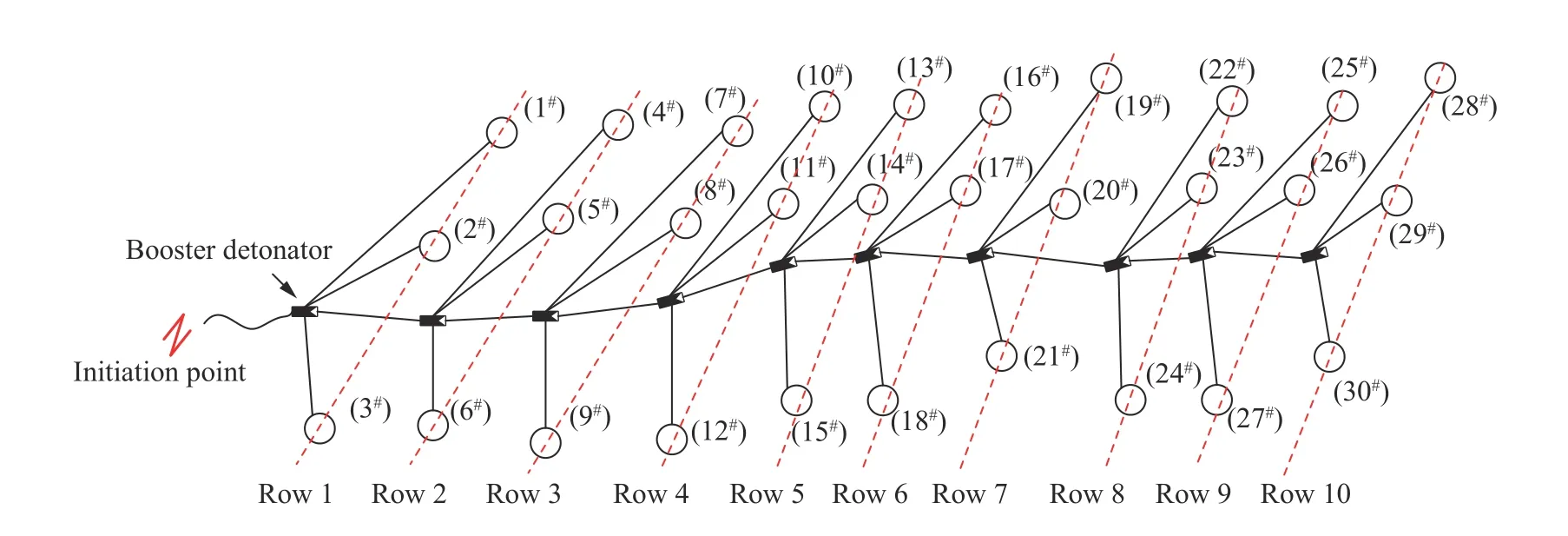
图2 毫秒延时起爆网路Fig.2 Initiation network of millisecond delay blasting

1.3 振动速度监测方案

爆破振动测试选用Mini-Blast Ⅰ型爆破振动速度测试系统，测试量程为0.001～35 cm/s，频响范围为1～500 Hz。为更好适应爆破试验现场环境，设置采集仪为自动工作模式，采样频率为10 000 s−1，数据采集时长设为8 s。

试验场地表面多为松散黏性土，为测得准确的爆破地震波时程信号，需确保振动速度传感器与地面刚性联接。因此，在各测点处清除表面松石与黏土，使用水泥砂浆抹平约0.1 m2，在水泥砂浆固化前水平预制埋入钻有螺纹孔的10 cm×10 cm×1.5 cm钢板，制作传感器固定基座，振动监测前通过扭紧螺丝将传感器与基座刚性联接[1]。

根据试验场地情况将测点尽可能布置在同一条测线方向上，测点布置方案如表3所示。振动速度监测方案如图3所示。

表3 测点布置方案Table3 Layout scheme of measuring points

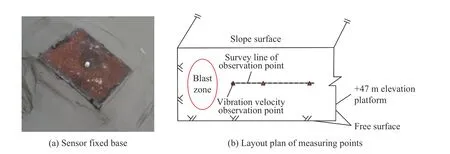
图3 振动速度监测方案Fig.3 Monitoring scheme of vibration velocity

1.4 数据分析与讨论

为研究爆破振动传播衰减规律，选取下述比例距离公式对振动实测数据进行回归分析[8-9]：

式中：vp为质点峰值振动速度，cm/s；k、α为场地条件相关系数，与爆破方式、装药结构、爆破点至监测点间的地形、地质条件密切相关[4]；R为爆心距，m；Q为最大单响药量，kg；Ds为比例距离[7]，m·kg−1/3。

本文中主要对各测点垂直向vp进行回归分析研究，爆破振动监测数据如表4所示。

表4 爆破振动测试数据Table4 Blasting vibration test data

为避免非电起爆网路中相邻段别地震波干扰叠加对等效药量取值的影响，从而影响回归分析结果导致vp预测误差。选取表4中两次单孔爆破振动监测数据进行回归分析，得到单孔爆破振速预测值vps随Ds的变化关系如图4所示。

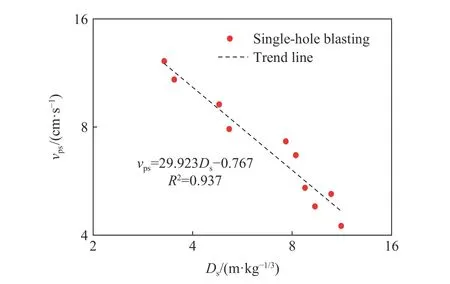
图4 单孔爆破振速随比例距离的变化关系Fig.4 Relation between blast vibration velocity for single-hole blasting and scaled distance

由图4可以看出，在对数坐标系情况下vps随Ds近似呈线性关系，通过线性回归得到试验场地单孔爆破振速vps预测公式为：

由于单孔爆破试验不存在分段地震波干扰叠加现象，各数据点中的峰值振速、单响药量及爆心距均严格一一对应，确保了回归分析数据集的准确性。同时，图4显示数据回归分析拟合度好，相关性达到0.937；并且应用式（2）计算得到vps预测值与实测值间均方根误差为0.55 cm/s，平均相对误差为7.39%，表明速度预测公式中的场地条件相关系数k=29.923，α=0.767可以真实反映试验现场装药结构、地质条件及地形相关属性特征，vps预测公式精度高，用于现场振动速度预测切实可行，具体数据可参见表5。

表5 单孔爆破振速的实测值与预测值对比Table5 Comparison of blast vibration velocity for single-hole blasting between measured and predicted values

2 群孔齐发爆破时等效装药量取值方法研究

炸药爆破引起岩土体高度非线性响应，线性叠加模型被用来预测全尺寸群孔爆破振动速度的效果不甚理想。Blair[28]依据比例药量法则，考虑单孔爆破时各装药单元对爆心距R处质点振动速度的非线性贡献特性，提出了爆破振动速度的叠加方法。

图5炮孔中总装药量为Q，共计M个装药单元，即Q=Mq，各装药单元距离振速监测点O处的距离为RM，各装药单元爆炸在O处激发的振动速度可通过下述非线性函数计算：

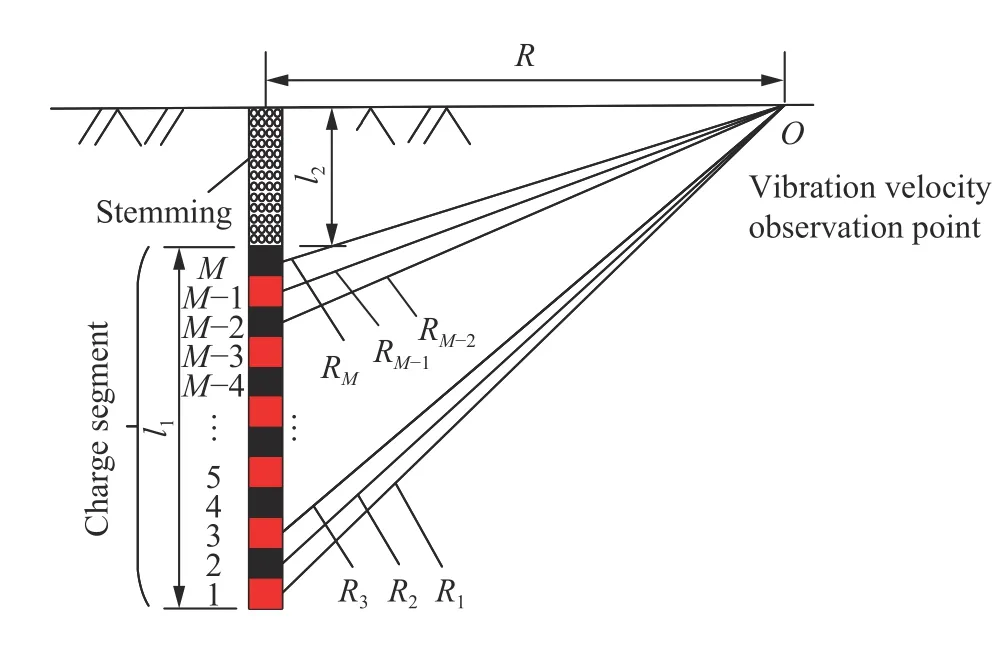
图5 单孔爆破振速叠加方法示意图Fig.5 Schematic diagram of superposition method for vibration velocity in single-hole blasting

式中：vpn为单孔爆破时第n个装药单元爆炸在O处激发的振动速度，cm/s；n为装药单元编号，n=1～M；A、B为与现场地质条件相关的系数；q为每个装药单元的TNT等效质量，kg。

因此，vp1=AqB。当R>>(l1+l2)时，R=RM，则整个炮孔装药量爆炸在O处引发的爆破振动速度为

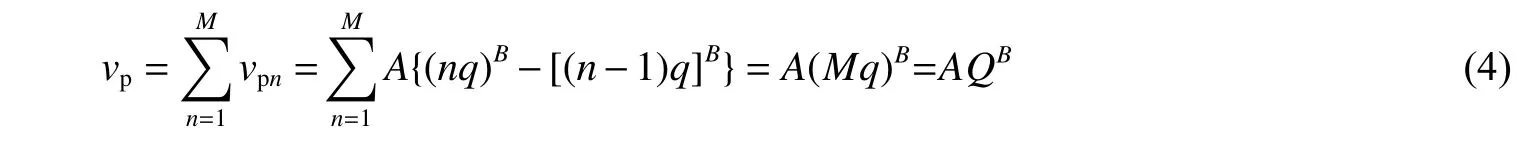
非电起爆网路中，假设将单孔药量Q平均分装到M个炮孔，建立群孔分散装药齐发爆破振速的计算模型，如图6所示。

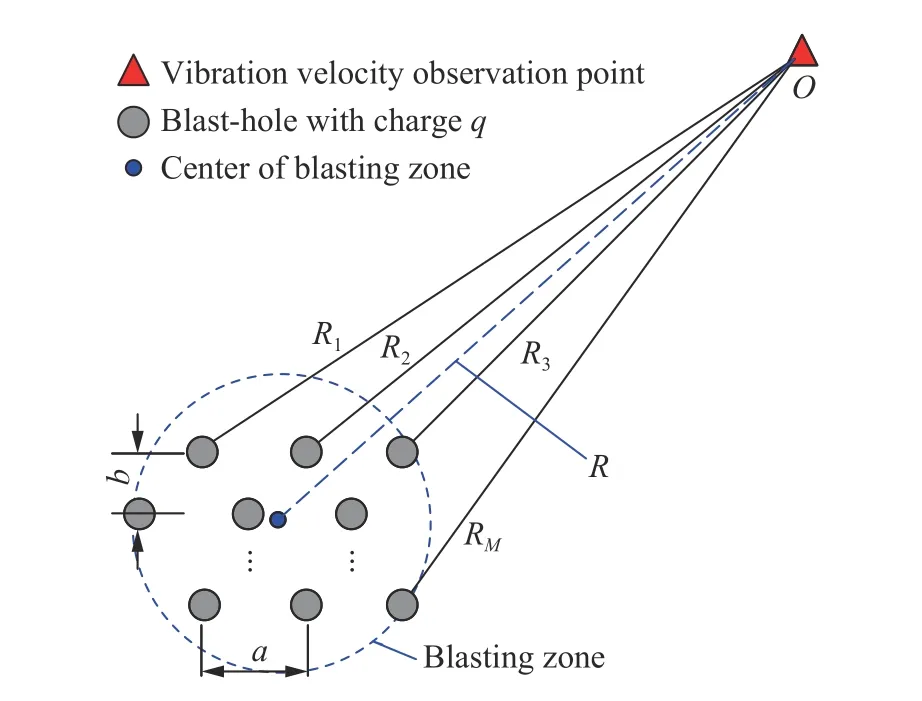
图6 群孔分散装药齐发爆破振速计算模型Fig.6 Calculation model of vibration velocity for simultaneous blasting of muti-hole with dispersed charge

因此，可应用式（3）依次计算得到每个炮孔（单孔药量为q）在振动观测点O处激发的振动速度。显而易见的是，由于炸药爆速极高，达到5 000 m/s以上[30-31]，图5单孔爆破时装药段完成爆轰所需时间非常短，炮孔内各装药单元可视为同时刻起爆。然而图6所示非电起爆网路群孔齐发爆破情况下，由于同段雷管延时误差的随机性及导爆管长度差异都可能导致各炮孔的起爆时刻存在时间差，并非严格意义上的同时起爆[32]。并且，各炮孔爆心距差异及振动波传播路径差异因素也会造成各孔爆炸地震波传播到振速观测点的时间差异。

其中导爆管长度及爆心距差异因素可通过人为控制，即组网时尽可能截取相同长度的导爆管，并将振动观测点距离延长、适当减小孔距。然而，导爆管雷管实际延期时间与其名义延期时间之间往往存在偏差（负延时偏差和正延时偏差），同时这些偏差在其置信区间内又是随机分布的，致使微差起爆网路跳段或重段现象时有发生[33-34]。实践中多排孔毫秒延时爆破情况下，往往孔外传爆雷管使用低段别，孔内起爆雷管采用高段别。同排炮孔齐发爆破时，炮孔内部起爆雷管均为相同段号的高段别雷管，若将传爆雷管点火计为0时刻，则可根据雷管延时偏差统计数据，分别计算出各炮孔的名义起爆时刻t0为孔内、外雷管名义延期时间之和，炮孔的最早起爆时刻t1为孔内、外雷管名义延期时间之和减去孔内、外雷管负延时偏差之和，炮孔的最迟起爆时刻t2为孔内、外雷管名义延期时间之和加上孔内、外雷管正延时偏差之和。

定义炮孔起爆时间窗T=[t1，t2]，因此可应用上述方法计算得到图6群孔齐发爆破时各炮孔的起爆时间窗如图7所示。

由图7可直观看出，由于雷管延时误差这一客观因素，无法确保齐发爆破时各炮孔在相同时刻起爆。因此，依据式（4）计算图6群孔齐发爆破振动速度时，由于各炮孔爆炸地震波并非同一时刻到达振速观测点，势必会造成振速观测点处各单孔爆炸地震波产生错峰现象，致使观测点处振动速度峰值水平偏低。这表明，群孔分散装药齐发爆破时等效药量取这些炮孔装药量的算术和是不合理的。Singh等[35]通过试验研究得到，在总药量相同情况下，单孔集中装药爆破和多孔分散装药齐发爆破振动速度相差最高可达55%，同一观测点处单孔爆破振动速度比齐发爆破振动速度高，印证了前述理论分析的正确性。同时，Singh等[35]提出在对齐发爆破等效药量进行取值时，可对炮孔数目取立方根到平方根进行折算，但并未明确何时取小值、何时取大值进行折算。

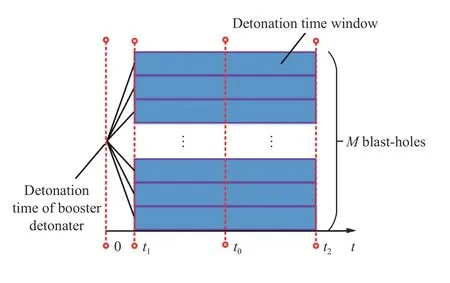
图7 各炮孔起爆时间窗Fig.7 Detonation time window for each blast-hole

这里引入缩比系数ƞ对炮孔数目M进行缩比处理，由数学概率理论可知，各炮孔在起爆时间窗长度范围内任一时刻起爆的概率均为P0=(t2−t1)−1，则群孔在同一时刻同时起爆的概率P=(t2−t1)−M。很显然，齐发爆破炮孔数目M越大，理论上同时起爆的概率P也就越小，考虑地震波错峰因素观测点处振动合速度越小，齐发爆破等效药量值则越小，炮孔数目的缩比系数ƞ应该越小。工程实践中，通常为确保起爆可靠性双发雷管绑扎不超过20根导爆管（20个炮孔）进行齐发爆破，即齐发爆破炮孔数2≤M≤20。因此，基于同时起爆概率P的函数特性及其对缩比系数ƞ的影响规律，缩比系数ƞ可通过下述指数函数进行计算：

式中：C、D为待定系数。且式（5）具有下述边界条件：

联合式（5）、（6）即可计算得到缩比系数ƞ随炮孔数目M的变化关系如图8所示。

由此艺术教育便吸引力我与我的合作者进行实践，并在领导老师的帮助下，开创了“执艺少儿美术启蒙班”，带着对艺术教育的理解，以及对于艺术教育的信心，面向5～9岁的小学生展开了课程的教学，带领他们体验艺术教育形式所具有的魅力，从而我们在课程编制、教学方式、教学理念等方面结合着艺术教育学有了很大的提高：

根据图8所示缩比系数ƞ随炮孔数目M的变化关系，可计算出本文毫秒延时起爆网路同段别炮孔数目的缩比系数ƞ=0.523×0.9783=0.489。因此，图2毫秒延时起爆网路中的最大单响药量Q=93×30.489kg=159.15 kg，则不同爆心距处的比例距离计算值见表4。

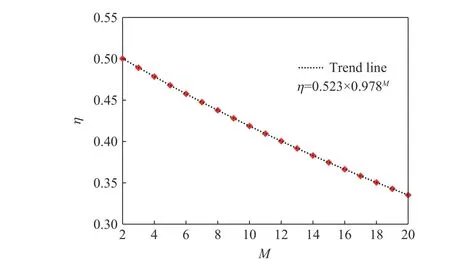
图8 缩比系数随炮孔数目的变化关系Fig.8 Variation relationship between the scaling factor and the blast-hole number

3 考虑振波叠加效应的毫秒延时爆破振速预测方法

在多孔毫秒延时爆破情况下，由于装药的空间分布、时间延迟和分段振波叠加影响，每延迟的准确单响药量是未知的，测点vp所对应的真实单响药量也不得而知。若仅仅依据起爆网路设计统计最大单响药量和爆破振动速度峰值，很难确保最大单响药量一定对应出现最大爆破振动速度，这样的简单统计方法会遗漏掉大量的振动分析信息，导致回归分析相关性差，甚至可能回归出奇异的k、α值[10,16]。另外考虑到vp预测方法应便捷、高效，从而便于爆破工程技术人员在现场选用。同时，从振动速度公式场地条件相关系数的物理意义出发，当施工现场地质、地形条件一定，且不改变装药结构和爆破方式的情况下，理论上场地条件相关系数（k、α）不应随起爆系统或爆破次数改变而发生变化[36]。基于此，若能在爆破现场应用单孔爆破振动速度回归分析得到的场地条件相关系数对群孔爆破振动速度进行准确预测则极为便利。

应用式（2）可计算得到毫秒延时爆破不同测点处振速预测值vps，如图9所示。

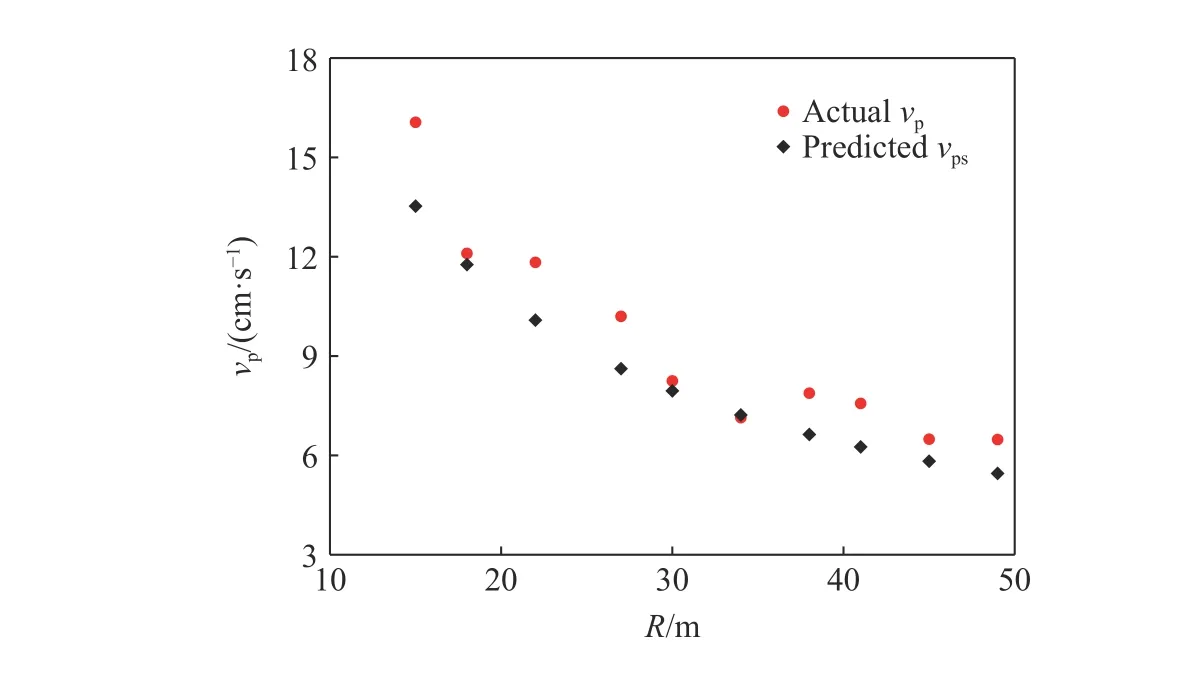
图9 毫秒延时爆破各测点峰值振动速度的实测值与预测值Fig.9 Actual and predicted particle peak vibration velocities at each measuring point in millisecond delay blasting

由图9可以看出，各监测点处vp预测值普遍比实测值要小。分析其原因，主要是由于毫秒延时爆破时，由于导爆管雷管客观的延时误差因素，导致分段振动波形间存在地震波主震相干扰叠加现象，从而使得实际最大单响药量与测点vp增大，此时若仍然应用式（2）计算毫秒延时爆破vp，则并未考虑分段振波的叠加影响，因此导致vp预测值普遍偏小。实测vp与预测vps随比例距离的变化关系如图10所示。

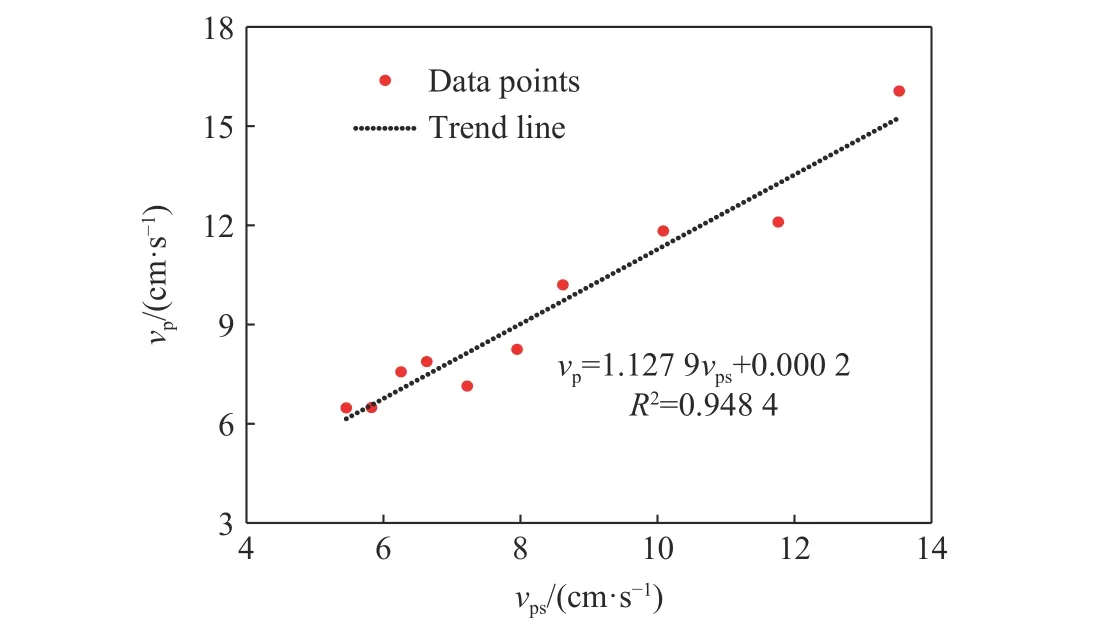
图10 实测vp与预测vps变化关系Fig.10 Relationship between actualvpand predictedvps

通过图10中数据的拟合分析，可得到vp实测值与预测值间的线性关系，拟合相关性达到0.948 4。因此，在考虑毫秒延时爆破分段振波叠加因素的基础上，修正的vp比例距离公式为：

将式（2）代入式（7）可得到：

因此，修正vp比例距离公式可表达为：

应用式（8）可计算得到现场试验不同测点处vp预测值，通过对比分析得到vp预测值与实测值间的相对误差平均值为6.42%，均方根误差为0.67 cm/s，表明修正的vp比例距离公式预测精度良好。

4 工程应用

某铅锌矿主要成矿元素为铅、锌和铁，经多次改扩建，实际采选生产能力达 5 000 t/d。矿体上下盘围岩稳固，岩石普氏硬度系数f=8～10，铅锌矿石f=8～12，矿石密度为3.6 t/m3，岩石密度为2.7 t/m3，矿岩松散系数为1.6。矿区范围内无大的地表水体，水文地质条件简单。为解决现场爆破大块率偏高、根底偏多和爆破振动对周边办公楼影响等问题，采用数码电子雷管进行毫秒延时爆破，段间间隔时间设定为25 ms。

设计开展现场单孔爆破振动监测试验，并对矿区4次生产爆破振动数据进行测试及分析，应用本文中提出的vp回归分析方法，爆破设计参数及vp预测值见表6。矿区实测vp值与预测vps值随比例距离的变化关系如图11所示。

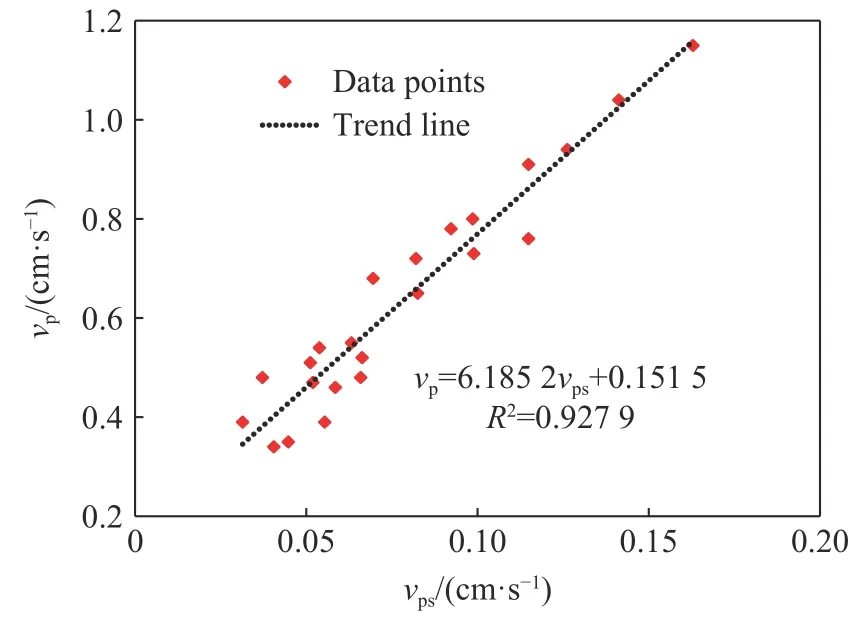
图11 矿区实例中vp实测值与预测值变化关系Fig.11 Relationship between actual and predicted vpvalues in mining area

依据矿区单孔爆破振动监测试验回归分析结果，得到了修正vp比例距离公式：

不同观测点处vp实测值与预测值的对比情况如图12所示。

由表6及图12可以得到，vp预测值与实测值间最大绝对误差为0.1 cm/s，平均绝对误差为0.05 cm/s，平均相对误差为9.52%，均方根误差为0.059 cm/s，在工程允许范围内。表明修正的比例距离公式及其回归分析方法，用于现场爆破振动速度预测与控制切实可行。

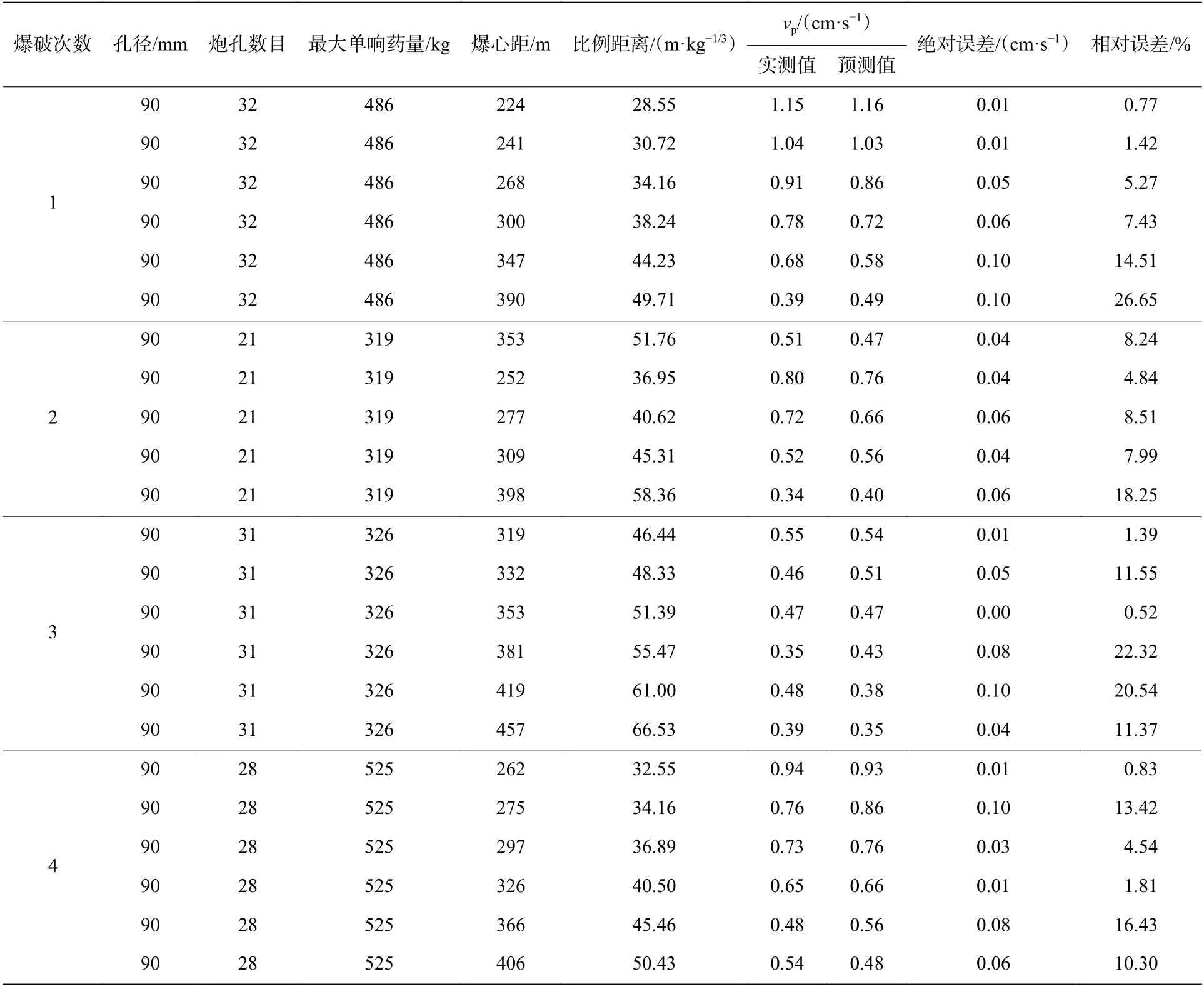
表6 爆破设计参数及vp值Table6 Blasting design parameters andvp values

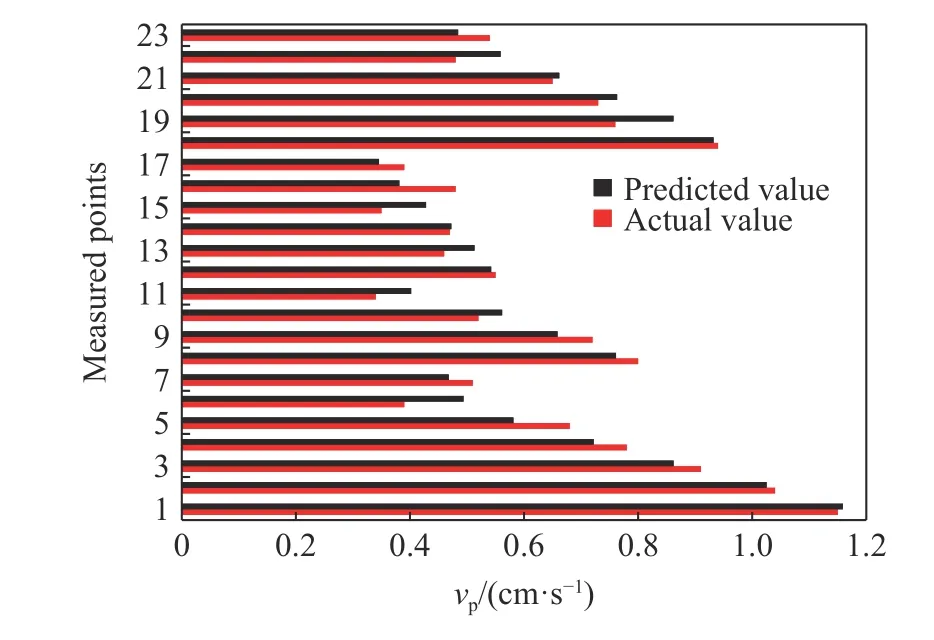
图 12 不同观测点处vp实测值与预测值的对比情况Fig.12 Comparison of the actual and predictedvpvalues at different observation points

5 结 论

毫秒延时爆破中分段爆破地震波存在干扰叠加现象，这对实际单响药量取值及振动速度准确预测造成了困难，本文中研究了群孔齐发爆破等效药量的取值方法，并考虑非电起爆网路分段振波叠加因素，对毫秒延时爆破振动速度回归分析方法进行了改进，主要得到以下结论。

（1）建立了群孔分散装药齐发爆破振速的计算模型，研究得到非电起爆网路在总药量相同情况下，群孔分散装药齐发爆破振动速度比单孔爆破振动速度小，齐发爆破等效药量比名义单响药量要小。

（2）提出了缩比系数ƞ的计算方法ƞ=0.523×0.978M，缩比系数ƞ随炮孔数目M的增加呈指数形式衰减；通过缩比系数折算炮孔数目计算齐发爆破等效药量，可使得计算结果更趋近实际单响药量。

（3）在单孔爆破振动速度回归分析的基础上，考虑毫秒延时爆破分段振波叠加效应，通过引入振波叠加因子ϕ，建立了毫秒延时爆破峰值振速的修正比例距离预测公式vp=kD−sα+ϕ 。试验条件下应用修正比例距离公式计算得到的vp预测值与实测值间的相对误差平均值为6.42%，均方根误差为0.67 cm/s，表明公式预测精度高。

（4）工程实例应用表明，应用修正比例距离公式计算得到的vp预测值与实测值间最大绝对误差为0.1 cm/s，平均绝对误差为0.05 cm/s，平均相对误差为9.52%，均方根误差为0.059 cm/s，用于现场爆破振动预测及控制切实可行。